页岩油气层地震岩石物理计算方法研究

刘喜武,刘宇巍,霍志周,刘志远,张剑锋,高红伟

(1.中国石油化工股份有限公司石油勘探开发研究院,北京100083;2.中国石油化工股份有限公司页岩油气勘探开发重点实验室,北京100083;3.国家能源页岩油研发中心,北京100083;4.中国科学院地质与地球物理研究所,北京100029)



页岩油气层地震岩石物理计算方法研究

刘喜武1,2,3,刘宇巍1,2,3,霍志周1,2,3,刘志远1,2,3,张剑锋4,高红伟4

(1.中国石油化工股份有限公司石油勘探开发研究院,北京100083;2.中国石油化工股份有限公司页岩油气勘探开发重点实验室,北京100083;3.国家能源页岩油研发中心,北京100083;4.中国科学院地质与地球物理研究所,北京100029)

摘要:研究通过数值计算地震波场特征直接获得地震波长尺度岩石物理参数及其响应特征的计算岩石物理方法。基于岩心资料,从页岩沉积的随机过程出发,以“层”和“纹层”为基本单元,构建厘米—毫米(cm—mm)级页岩小尺度数值地质模型,并随机加入有机质、有机孔、层间缝、垂直缝和基质孔隙。在小尺度网格应用宏观岩石物理等效介质模型,充分考虑介质的非均匀性,将小尺度地质模型转化为地球物理参数模型。基于小尺度地质模型与小网格地球物理参数模型,进行不同角度平面非均匀地震波传播模拟,提取传播时差,直接计算得到地震波长尺度的岩石物理参数。以胜利油田罗家地区页岩油层为例,改变TOC含量、层与纹层不同厚度和组合、裂隙分布,分别计算弹性参数,并甄选敏感弹性参数,验证了方法的有效性。

关键词：小尺度地质建模;等效介质理论;格子法地震波场模拟;计算岩石物理

页岩油气已成为非常规油气勘探开发的重要领域之一。由于页岩油气层的微观复杂性、非均匀性和各向异性,纳米级尺度的储集空间和甜点要素的宏观地球物理响应规律不清楚[1]。如何获得泥页岩纹层发育程度、有机质丰度(TOC)、有机孔、基质孔、微裂隙、裂缝等岩石参数与地震响应特征的关系,是岩石物理和地球物理面临的挑战,也是地球物理甜点预测的基础。目前,针对页岩油气储层的岩石物理模型和响应特征研究[2-6],存在储层微观尺度与地震宏观尺度不匹配的问题[7],如何获得真实地震波场尺度和频率段下的页岩油气层岩石物理参数和地震响应规律,对于实验岩石物理来说面临较大挑战,而且基于实验室物理测量的方法和基于数字岩心图像处理的计算岩石物理方法,均不能直接获得地震波场的动态岩石物理弹性参数[8]。

地震计算岩石物理方法是一个比较新的概念,就是试图利用地震波场数值模拟计算方法获取弹性参数,解决岩石物理实验测量面临的样品不足、尺度效应等问题,特别是对各向异性、衰减等特征的测量。目前地震岩石物理计算方法仍然处于小尺度地震波场模拟探索阶段,尚未形成有效技术[8]。需要指出,岩石物理实验和计算岩石物理是相互促进的,计算岩石物理并不能取代岩石物理实验,地震波传播模拟的一些基本参数还是需要由岩石物理实验来准确测定,例如,在不同温压条件下不同岩石组分的弹性模量、裂缝的柔度系数等。

本文首先阐述小尺度地质数值建模、非均匀网格介质等效地球物理参数建模、非均匀非结构网格地震波场数值模拟、地震波计算岩石物理方法,探索建立一套有别于实验岩石物理、数字岩石物理的地震波计算岩石物理方法,并形成一种新的页岩油气层地震岩石物理参数计算方法;最后,以胜利油田罗家地区页岩油储层为例,应用提出的地震波计算岩石物理方法提取弹性参数,分析响应特征和响应规律,甄别敏感弹性参数,为页岩油气层岩石物理分析和地震甜点预测研究提供新的思路与手段。

1页岩小尺度地质与地球物理参数建模方法

从页岩沉积的随机过程出发,采用二维马尔科夫链模型[9-11],以“层”和“纹层”为基本单元,构造地震波长尺度(100m左右)的页岩模型。首先,通过分析已知岩心样品,定义不同类型岩相的“层”或“纹层”基本单元;然后,估计转移概率矩阵,生成非均匀波长尺度页岩模型。具体步骤为：①根据典型岩心样品分析结果,决定岩相、层结构和矿物组分含量;②确定“层”和“纹层”基本单元及其成分;③综合考虑岩心样品统计分析结果和成分含量,确定转移概率矩阵;④确定不同深度区间“层”和“纹层”的比例和分布模式;⑤随机加入有机质(包括有机孔),根据“层”和“纹层”泥质含量大小,确定有机质的发生概率,获得非均匀的有机质分布;⑥随机加入层间缝、垂直缝;⑦依据岩心样品统计得到的孔隙率,加入孔隙。

在小尺度地质建模的基础上,划分小尺度网格(0.001m×0.001m),对网格内包括的非均匀矿物,考虑孔隙,采用自洽理论(self-consistent approximation,SCA)、Brown-Korring广义Gassmann理论、Hudson裂缝等效理论等生成等效的物理参数[12]。业界通用的岩石物理建模方法是将上述理论直接应用于整体模型,计算宏观响应参数。本文研究将其应用于各个小尺度网格上进行等效,这就充分考虑了实际页岩的强非均匀性。具体等效步骤与通用岩石物理建模方法一致：①采用SCA计算不同成熟度干酪根的物理参数(考虑有机孔);②采用SCA计算含泥、干酪根、石英、方解石、孔隙的干岩石模量;③采用Wood公式计算孔隙中气、水、油构成的混合流体的密度和体积模量;④采用Brown-Korring广义Gassmann方程进行孔隙混合流体替换;⑤采用Hudson公式引入层间缝,对介质加入各向异性特征。

2地震岩石物理计算方法原理

图1　格子法波场模拟网格计算示意图解

(1)

式中：Mi为虚线轮廓线包围的质量,它是i点周围三角形质量(面积乘密度)和的1/3(在本项目计算中仅用三角形离散);(bi)l和(ci)l为对应三角形的形状系数;(σx)l,(σz)l和(τxz)l是各个三角形形心处的应力;ut和wt分别为x方向和z方向的速度分量。

根据纵、横波不同方向入射的波场传播时间差可以计算弹性参数。如图2所示,通过计算纵波通过尺寸为L的模型的起始时间与结束时间,可计算波场传播时间差Δt。(2)式为垂直入射的纵波速度计算公式,(3)式为各向异性参数计算公式。

(2)

式中：vP为纵波速度;L为模型尺寸;Δt为波前记录的时差;v0为给定的均匀介质纵波速度;x1和x2分别为波前位置。

图2　小尺度地质模型纵波波场传播快照

(3)

式中：v(θ)为不同入射角θ的P波速度;ε和δ为各向异性参数。

计算得到纵、横波速度后,相应的可以采用(4)式 和(5)式计算杨氏模量、泊松比等弹性参数(各向同性介质)。

(4)

(5)

式中：ρ为密度;vP为纵波速度;vS为横波速度。

3实际应用效果分析

以胜利油田罗家地区页岩油层为例,地震岩石物理计算方法实际应用流程如图3所示。页岩小尺度地质建模以罗69井为例确定层、纹层结构以及矿物成分,孔隙添加依据岩心样品统计结果,层间缝和垂直缝随机加入;将宏观等效岩石物理方法用于小尺度网格(0.001m×0.001m)进行地球物理参数建模;为提高地震波场模拟时差提取的精度,将地质模型进行了叠置,并放在一个均匀背景介质中,分别计算TOC变化和裂隙密度变化的弹性参数,分析敏感弹性参数。

图3　地震岩石物理计算流程

3.1小尺度地质与地球物理参数建模

根据实际岩心分析得到的主要岩相组合和矿物成分,认为页岩储层非均匀的关键因素为：纹层结构、层结构、矿物成分;根据地质录井和测井评价结果,将“层”的尺度定义在“10cm”量级,将“纹层”的尺度定义在“mm”量级,而将横向非均匀的尺度定义在“10m”量级;矿物组分主要考虑：粘土、方解石、石英、有机质。确定的3种“层”单元为：含泥质灰岩层、泥质灰岩层、灰质泥岩层(0.1m×10.0m),确定两种“纹层”单元：灰质纹层、泥质纹层(0.001m×10.000m)。孔隙空间考虑基质孔隙、有机孔和裂缝。

需指出的是,尽管“层”单元的尺度为0.1m×10.0m,但这一单元在地质模型中实际上是由100×10000个离散点构成的,依据单元的矿物成分,这些离散点将分别对应方解石、粘土或石英这几种基本矿物;同理,“纹层”单元是由1×10000个离散点构成的,这些离散点将分别对应方解石、粘土、石英或有机质等几种基本矿物,即可产生0.001m×0.001m分辨率的小尺度模型。依据上述策略,利用地层沉积的马尔科夫链过程和矿物成分含量来随机生成小尺度、精细地质模型,并在小尺度网格等效计算地球物理参数。图4和图5分别给出了页岩油工区的层状和纹层状模型数值计算结果。图中黄色样点代表方解石;深蓝色样点代表粘土;天蓝色样点代表石英;红色样点代表TOC。右侧岩心扫描照片为示意图,说明小尺度数值地质建模能够反映页岩层结构特征。

图6为小尺度岩石物理等效方法宏观测试结果。将给出的岩石物理等效方法用于预测测井曲线。图中蓝色曲线为预测的纵波曲线;红色曲线为预测的横波曲线;右侧为相应的预测误差曲线。纵波曲线预测误差很小,横波曲线预测的误差最大为20m/s,表明采用的介质等效方法和步骤是有效的。介质等效建模考虑了页岩的各种要素,能够满足小尺度地球物理参数建模的需要。基于岩石物理等效方法在小尺度网格计算得到小尺度地球物理参数。

3.2地震计算岩石物理参数提取与响应规律研究

以小尺度地质模型为基础,进行基于波场模拟的地震弹性参数计算与提取分析。为充分反映非均匀页岩储层的尺度效应,提高地震波传播时差提取的精度,基于上述参数生成厚度100m(接近一个波长)、宽1000m的地质模型,生成的页岩模型重复铺设,并且放置到一个均匀介质中,得到更大的模型(图7)。采用格子法进行地震波场模拟,图8 为倾斜平面波穿过储层的波场快照(图中两条黑线所夹的区域为储层)。

图4　数值计算得到的页岩层状小尺度地质模型(右侧为岩心扫描照片)

图5　数值计算得到的页岩纹层状小尺度地质模型(右侧为岩心扫描照片)a 生成的纹层状岩相局部(1); b 生成的纹层状岩相局部(2)

图6　某页岩油井纵、横波速度等效介质模拟结果

图7　地震波场模拟采用的模型

在地震波场模拟的基础上,提取计算弹性参数,研究地震响应特征与规律。计算表明：随TOC的增加速度降低,随裂缝密度增加速度也降低,与实验室及其理论岩石物理研究规律和结论相一致[3]。在研究纵、横波速度和各向异性参数变化规律的基础上,综合考虑储层各向异性参数和地震波速度,建议TOC和裂缝密度预测的敏感参数为：ε/vP,δ/vP。图9和图10分别给出了敏感弹性参数与TOC以及裂缝密度(主要是水平顺层缝)的变化关系;图11和图12分别给出了杨氏模量、泊松比等弹性参数与TOC和水平顺层缝裂隙密度变化的关系。由图9到图12可以看出,TOC和裂缝密度预测的敏感参数分别为脆性(负相关)、ε/vP(正相关)和δ/vP(正相关)。注意到当水平顺层缝足够大时,出现负泊松比现象,解释为：轴向拉伸、裂缝导致横向膨胀。

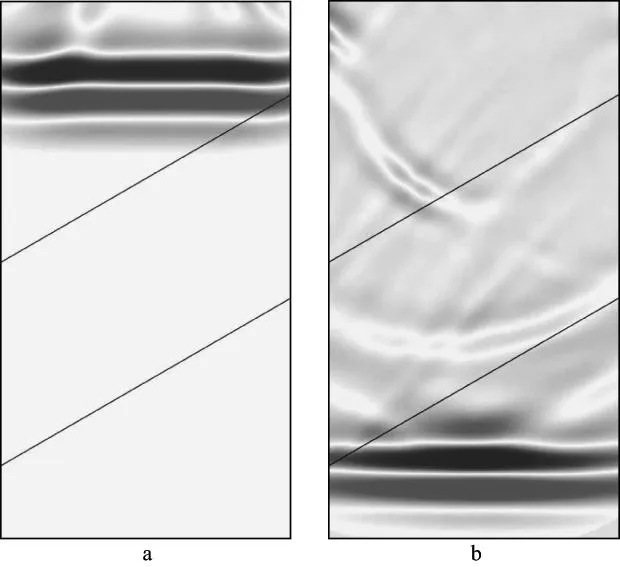
图8　倾斜平面P波穿过储层的波场快照a 倾斜入射波场; b 倾斜出射波场

图9　敏感弹性参数ε/vP(a)和δ/vP(b)与TOC含量变化的关系

图10　敏感弹性参数ε/vP(a)和δ/vP(b)与裂缝密度变化的关系

图11　杨氏模量(a)、泊松比(b)与TOC变化的关系

图12　杨氏模量(a)、泊松比(b)与水平裂缝密度变化的关系

4结束语

1) 探索建立了一套页岩油气层地震岩石物理计算方法,包括小尺度地质与地球物理参数建模、非均匀地震波场模拟和参数计算,为明确页岩油气层地球物理响应规律,提供了一种全新的计算岩石物理手段。

2) 针对胜利油田罗家地区页岩油储层,充分考虑页岩岩相、层和纹层结构、矿物成分,考虑基质孔隙、有机孔、裂隙特征,应用地震计算岩石物理方法,建立微观复杂性与宏观地震弹性参数之间的关系,综合考虑储层各向异性参数和地震波速度,建议TOC和裂缝密度预测的敏感参数选为ε/vP和δ/vP;可进一步研究单参数、组合参数变化下的弹性参数变化规律,甄选甜点预测敏感弹性参数。

3) 地震岩石物理计算方法的优势在于克服了实验条件和岩心样品的限制,通过数值模拟获得地震波长尺度的岩石物理参数,得到物理实验很难直接获得的参数,如衰减特征、各向异性特征;不足之处在于过程和参数复杂,计算量大,需要并行计算,也需要岩石物理实验提供基本参数。

参考文献

[1]刘振武,撒利明,杨晓,等．页岩气勘探开发对地球物理技术的需求[J]．石油地球物理勘探,2011,46(5)：810-818

LIU Z W,SA L M,YANG X,et al.Needs of geophysical technologies for shale gas exploration[J].Oil Geophysical Prospecting,2011,46(5):810-818

[2]MAVKO G,MUKERJI T,DVORKIN J.The rock physics handbook[M].Cambridge:Cambridge University Press,2009:1-10

[3]ZHU Y P,LIU E R,ALEX M,et al.Understanding geophysical responses of shale-gas plays[J].The Leading Edge,2011,30(3):332-338

[4]GUO Z Q,LI X Y,LIU C.Anisotropy parameters estimate and rock physics analysis for the Barnett Shale[J].Journal of Geophysics and Engineering,2014,11(6):1-11

[5]LI Y,GUO Z Q,LIU C,et al.A rock physics model for the characterization of organic-rich shale from elastic properties[J].Petroleum Science,2015,12(2):264-272

[6]WU X,CHAPMAN M,LI X Y,et al.Anisotropic elastic modeling for organic shales[J].Expanded Abstracts of 74thEAGE Conference & Exhibition,2012:314-318

[7]BAYUK I O,AMMERMAN M,CHESNOKOV E M.Upscaling of elastic properties of anisotropic sedimentary rocks[J].Geophysical Journal International,2008,172(2):842-860

[8]陈颙,黄庭芳,刘恩儒.岩石物理学[M].合肥：中国科学技术大学出版社,2009:400-475

CHEN R,HUANG T F,LIU E R.Rock physics[M].Hefei:China University of Science and Technology Press,2009:400-475

[9]WANG G C,TIMOTHY R.Methodology of organic-rich shale lithofacies identification and prediction:a case study from Marcellus Shale in the appalachian basin[J].Computers & Geosciences,2012,49:151-163

[10]KALE S V,RAI C S,SONDERGELD C H.Petrophysical characterization of Barnett Shale[C].SPE Unconventional Gas Conference Expanded Abstracts.Pittsburgh,Pennsylvania,USA:SPE,2010:17

[11]MICHELENA R J,GODBEY K S,ANGOLA O.Constraining 3D facies modeling by seismic-derived facies probabilities:example from the tight-gas Jonah field[J].The Leading Edge,2009,28(12):10-19

[12]刘喜武,董宁,刘宇巍.裂缝性孔隙介质频变AVAZ反演方法研究进展[J].石油物探,2015,54(2)：210-217

LIU X W,DONG N,LIU Y W.Progress on frequency-dependent AVAZ inversion for characterization of fractured porous media[J].Geophysical Prospecting for Petroleum,2015,54(2):210-217

[13]ZHANG J F,LIU T L.P-SV-wave propagation in heterogeneous media:grid method[J].Geophysical Journal International,1999,136(2):431-438

[14]ZHANG J F,VERSCHUUR D J.Elastic wave propagation in heterogeneous anisotropic media using the lumped finite element method[J].Geophysics,2002,67(2):625-638

[15]ZHANG J F,LIU T L.Elastic wave modelling in 3-D heterogeneous media:3-D grid method[J].Geophysical Journal International,2002,150(3):780-799

[16]GAO H W,ZHANG J F.Parallel 3-D simulation of seismic wave propagation in heterogeneous anisotropic media:a grid method approach[J].Geophysical Journal International,2006,165(3):875-888

[17]ZHANG J F.Elastic wave modeling in fractured media with an explicit approach[J].Geophysics,2005,70(5):T75-T85

[18]ZHANG J F,GAO H W.Elastic wave modelling in 3D fractured media:an explicit approach[J].Geophysical Journal International,2009,177(3):1233-1241

(编辑：陈杰)

Study on seismic rock physics computational method for shale reservoir

LIU Xiwu1,2,3,LIU Yuwei1,2,3,HUO Zhizhou1,2,3,LIU Zhiyuan1,2,3,ZHANG Jianfeng4,GAO Hongwei4

(1.PetroleumExplorationandProductionResearchInstitute,SINOPEC,Beijing100083,China;2.SinopecKeyLaboratoryofShaleOil/GasExplorationandProductionTechnology，Beijing100083,China;3.NationalEnergyResearch&DevelopmentCenterofShaleOil，Beijing100083，China;4.InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China)

Abstract:A new scheme for shale rock physics study is presented.Firstly,Small-scale shale geological model is computed by considering layer,fine-layer,TOC,crack and porosity.Then,Geophysical properties are computed on non-uniform small grids by effective medium theory with heterogeneity being considered.Finally,seismic modeling is utilized to compute seismic elastic parameters by traveltime difference based on the small-scale geological model and the small grid geophysical parameters model.The methods are applied to shale oil area in Shengli Oilfield and seismic responses are variation of TOC and crack density.The results demonstrate the effectiveness of the proposed method,which have the similar trends with lab data and theoretical data by cross plot for variation of TOC and crack density with elastic parameters,especially with anisotropic parameters.

Keywords:small-scale geological modeling,effective medium theory,grid method seismic modeling,computational rock physics

文章编号：1000-1441(2016)01-0010-08

DOI:10.3969/j.issn.1000-1441.2016.01.002

中图分类号：P631

文献标识码：A

基金项目：国家重点基础研究发展计划(973计划)项目(2014CB239104和2012CB214806)资助。

作者简介：刘喜武(1970—),男,副教授,主要从事页岩油气地球物理与地震各向异性裂缝预测研究工作。

收稿日期：2015-07-24;改回日期：2015-08-05。

刘喜武,刘宇巍,霍志周,等.页岩油气层地震岩石物理计算方法研究[J].石油物探,2016,55(1):-17

LIU Xiwu,LIU Yuwei,HUO Zhizhou,et al.Study on seismic rock physics computational method for shale reservoir[J].Geophysical Prospecting for Petroleum,2016,55(1):-17

This research is financially supported by the National Key Basic Research Program of China (973 Program) (Grant Nos.2014CB239104,2012CB214806).