基于MATLAB汽车发动机配气凸轮的型线设计与接触应力分析*

陈晨，王自勤，田丰果，陈家兑，徐玉梁

(贵州大学现代制造技术教育部重点实验室，贵州贵阳550003)



基于MATLAB汽车发动机配气凸轮的型线设计与接触应力分析*

陈晨，王自勤，田丰果，陈家兑，徐玉梁

(贵州大学现代制造技术教育部重点实验室，贵州贵阳550003)

摘要：在汽车发动机配气凸轮的型线设计过程中，通过选用合适型线函数，设定预期从动件运动边界条件，推导凸轮接触应力计算公式，进而通过MATLAB编程，可生成预设的从动件升程、速度、加速度和凸轮接触应力曲线。文中所涉及的MATLAB程序以期快速完成凸轮设计和分析凸轮接触应力为目的，应用此方法可显著提高配气凸轮设计的速度和精度，并为凸轮机构的优化提供理论依据。

关键词：配气凸轮型线设计MATLAB接触应力

0引言

凸轮机构具有结构紧凑、可精确实现复杂运动规律等特点而被广泛用于在汽车发动机配气机构中[1]。配气机构的性能指标在很大程度上取决于它的主动件,配气凸轮的型线[2]。而在配气机构中，配气凸轮与从动件之间的摩擦是一对重要的摩擦副，若两者接触应力过大，容易导致磨损、擦伤和劈裂等故障，进而影响配气机构的正常工作。在设计凸轮型线时，需要计算并校核凸轮与从动件之间的接触应力[3]，然而由于凸轮轮廓的曲率半径随凸轮转角的变化而改变，将动力学问题考虑进去将致使接触应力计算量加大，要得到凸轮转角与凸轮接触应力的关系，用传统计算手段难以在工程中实现。

目前已有的研究多集中在凸轮型线设计或凸轮接触应力计算分析的单方面研究上，两者同时进行设计计算较少。本文作者示例了一种通过MATLAB编程，应用其强大的数据处理能力，在设计凸轮型线的同时也完成了凸轮与从动件的接触应力的计算，并可直观的得到凸轮从动件位移、速度、加速度曲线以及凸轮各转角处的接触应力曲线图像，便于对气门的状态和凸轮与从动件之间接触应力进行分析，在为凸轮机构的优化提供理论依据同时，也可显著提高配气凸轮设计的速度和精度。

1凸轮型线函数的确定

凸轮型线由缓冲段和工作段两部分组成[4]。缓冲段曲线种类很多，本文以等加速-等速型为例。

与凸轮设计常用的其他型线相比，高次多项式凸轮型线因具有良好的整体连续性和升程曲线高阶连续性等特点，使发动机的配气机构获得良好的运动平稳性和动力学特性[5]，而被广泛的应用。在设计时，高次多项式常取五至七项，而第六项以后对动力性能指标的影响已经很小，且随着高次多项式项数的增加，凸轮丰满系数减小，加速度的绝对值变大，凸轮机构的工作性能下降[6]。鉴于上述原因，本文中的凸轮工作段的型线以五次多项式为例进行设计计算。

2从动件升程函数与边界条件

文中的凸轮型线采用对称形式，只设计上升段，再将上升段函数对称得出下降段。

凸轮缓冲段从动件升程曲线函数表示为：

(1)

凸轮工作段从动件升程曲线函数表示为：

s(α)=C4α5+C5α4+C6α3+C7α2+C8α+C9

α2≤α≤α3

(2)

其中：Ci，i=1-9，为待定系数；α0为缓冲段起始点；α1为缓冲段分界点；α2为缓冲段终点(工作段起始点)；α3为工作段终点；α为凸轮转角，单位：°。

根据从动件的运动规律确定升程函数的边界条件，现取α0=0°、α1=10° 、α2=15°、α3=80°。

当α=0°时：

当α=10°时：s(α)=0.06

当α=15°时：

当α=80°时：

3接触应力公式推导

对于平底从动件盘形凸轮机构，平底从动件与凸轮轮廓理论上为线接触，但在受载情况下，由于材料的弹性变形，实际上为很小的面接触，且最大接触应力发生在接触区中线上[7-8]。接触面上的最大接触应力按弹性理论中的赫兹公式计算：

(3)

式中：Fn为凸轮与平底从动件接触处法向载荷，N；

ρ1、ρ2分别为凸轮实际轮廓线的曲率半径和平底从动件曲率半径，mm；

b为凸轮与平底从动件的接触线长度，mm；

μ1、μ2分别为凸轮与从动件材料的泊松比；

E1、E2分别为凸轮与从动件材料的弹性模量，MPa。

由于平底从动件的曲率半径趋于无穷大，即ρ2→∞，本文中凸轮与平底从动件采用同种材料制成，故赫兹公式变为：

(4)

式中：E为凸轮与平底从动件采用同种材料的弹性模量，MPa；

ρ为凸轮实际轮廓线的曲率半径，mm；

μ为凸轮与平底从动件采用同种材料泊松比。

4接触应力所需参数确定

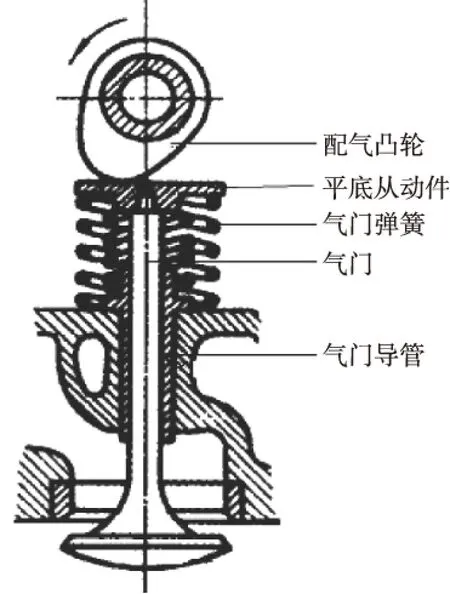
图1　顶置配气凸轮机构

顶置配气凸轮机构如图1所示。某型号发动机进气门质量m1=48.2g，平底从动件质量m2=17.3g，气门弹簧质量m3=32.2g，气门弹簧刚度K=50N/mm，预紧力F0=260N，接触线长度为b=12mm。本文所示例的为常见的钢制凸轮机构，则有：μ=0.3，E=206GPa。由于该机构的从动件是平底的，可知压力角为0，则弹簧作用于凸轮上的力即为凸轮与平底从动件接触处法向载荷，即：

Fn=K·s+F0+m·a

(5)

m=m1+m2+m3/3

(6)

式中：a为从动件的加速度(m/s2)。

而凸轮实际轮廓线的曲率半径ρ，为凸轮转角α的函数。由高等数学可知，凸轮轮廓理论廓线曲率半径用极坐标形式表示为：

(7)

式中：R为矢径。

5编辑MATLAB程序

利用MATLAB软件编辑凸轮工作段函数系数求解、从动件升程曲线、不同转速下的从动件速度曲线、不同转速下的从动件加速度曲线以及不同转速下凸轮转角α与凸轮接触应力σH的关系曲线的程序[9]。部分程序代码如下：

clc

clear

syms x C4 C5 C6 C7 C8 C9

format long

s=C4*x^5+C5*x^4+C6*x^3+C7*x^2+C8*x+C9;

s1=diff(s,x);

s2=diff(s,2,x);

s11=subs(s,x,15);

s12=subs(s1,x,15);

s13=subs(s2,x,15);

s14=subs(s,x,80);

s15=subs(s1,x,80);

s16=subs(s2,x,80);

A=[s11;s12;s13;s14;s15;s16];

B=double([subs(A,[C4 C5 C6 C7 C8 C9],[1,0,0,0,0,0]),...

subs(A,[C4 C5 C6 C7 C8 C9],[0,1,0,0,0,0]),...

subs(A,[C4 C5 C6 C7 C8 C9],[0,0,1,0,0,0]),...

subs(A,[C4 C5 C6 C7 C8 C9],[0,0,0,1,0,0]),...

subs(A,[C4 C5 C6 C7 C8 C9],[0,0,0,0,1,0]),...

subs(A,[C4 C5 C6 C7 C8 C9],[0,0,0,0,0,1])]);

D=[0.12;0.012;0;8;0;-0.012];

rank(B,D)

..........

aa33=(xx(1)*20*w22^2*n3.^3+xx(2)*12*w22^2*n3.^2+xx(3)*6*w22^2*n3+...

xx(4)*2*w22^2)/1000；

f33=k*s3+f0+m*aa33；

q33=sqrt(f33*E./(2*pi*b.*p3*(1-u^2)))；

plot(n3,q33,′-.k′)；

hold on

legend(′800r/min′,′1500r/min′,′3500r/min′);

set(gca,′xtick′,0∶10∶160,′ytick′,240∶10∶330);

xlabel(′凸轮转角 /alpha(度)′);

ylabel(′接触应力/sigma_H(MPa)′);

6从动件的升程、速度、加速度和凸轮接触应力分析

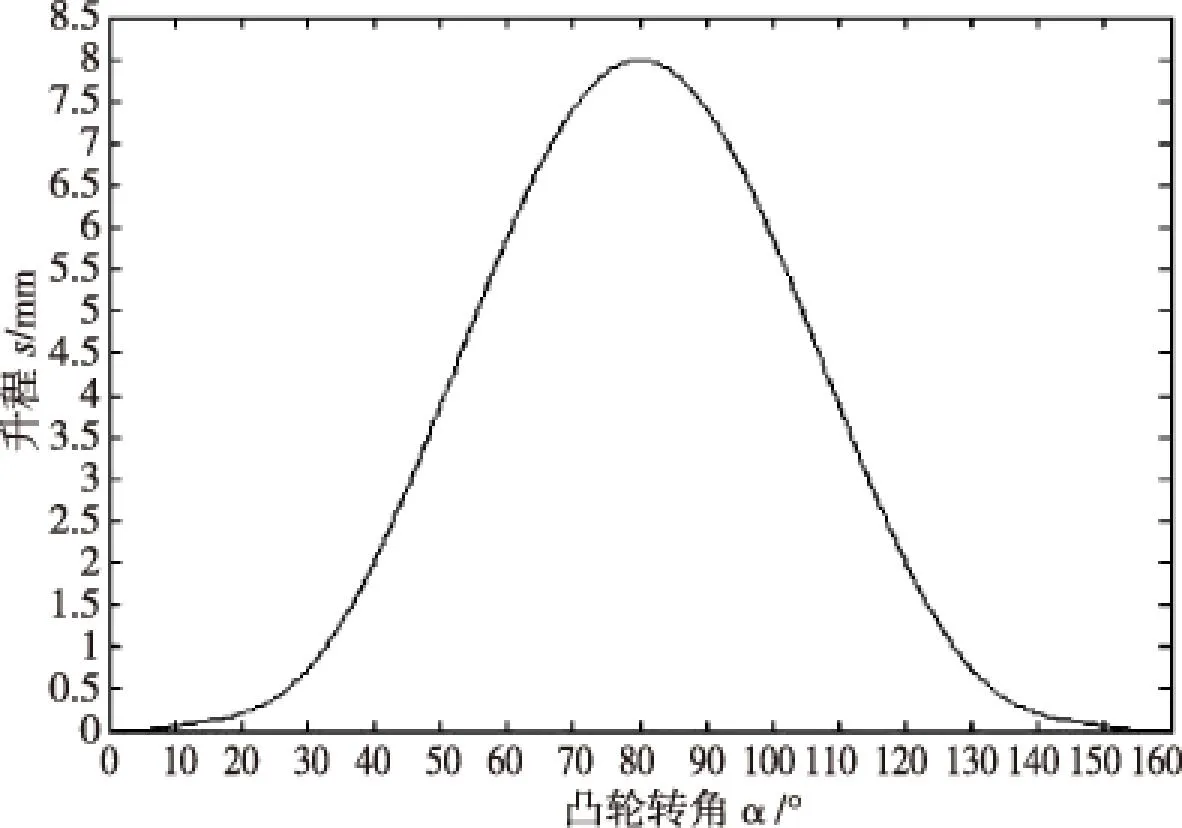
图2　从动件升程曲线

运行上述编辑的MATLAB程序，生成从动件升程曲线，如图2所示；发动机在转速变化时，不同转速下的从动件速度曲线，如图3所示；不同转速下的从动件加速度曲线，如图4所示；不同转速下凸轮转角α与凸轮接触应力σH的关系曲线，如图5所示。

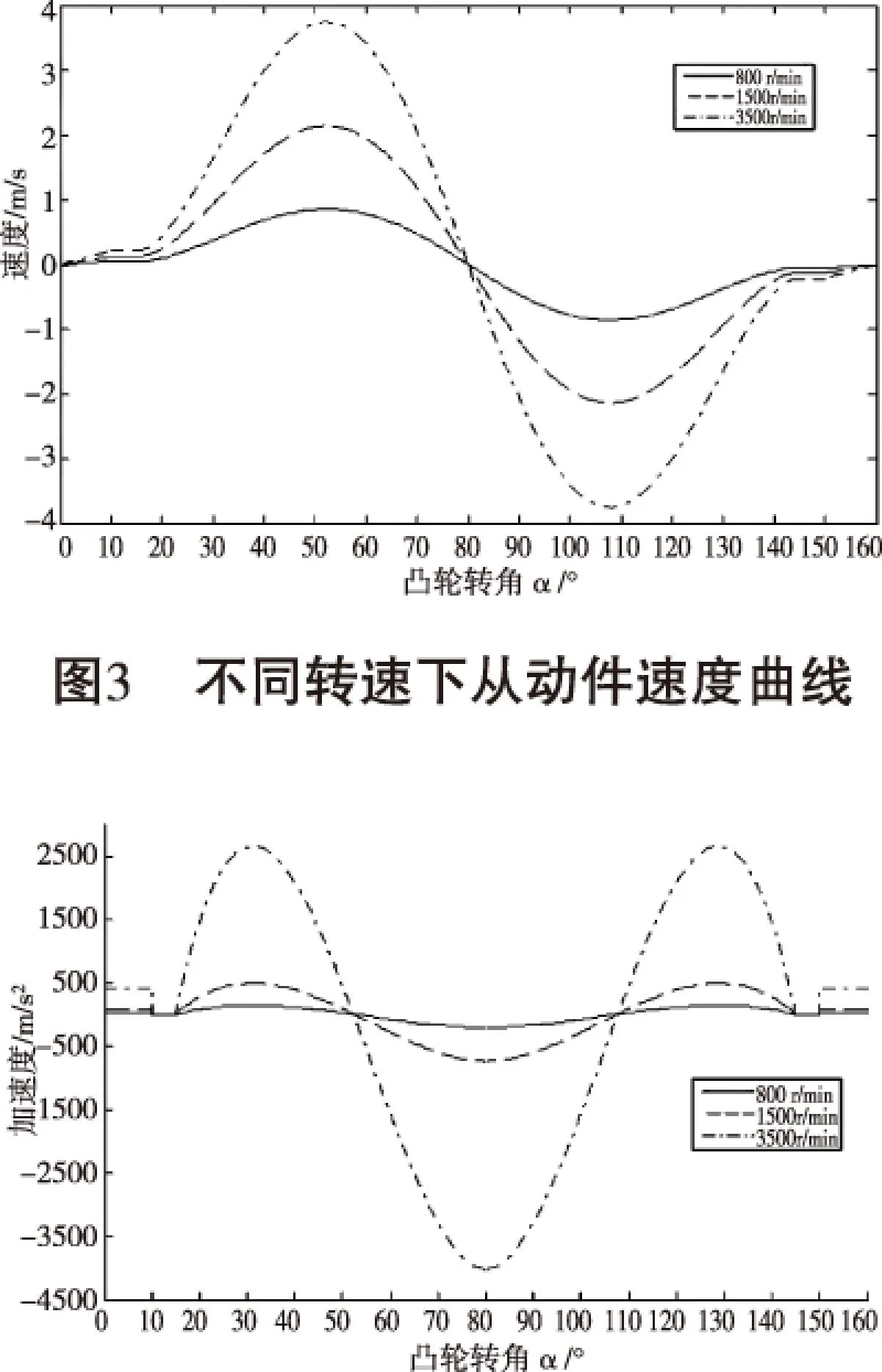
图4　不同转速下从动件加速度曲线

从上述图可以看出，当发动机运行转速分别为800 r/min、1 500 r/min、3 500 r/min时，从动件最大速度都发生在53°处，分别为0.877 m/s、2.117 m/s和3.731 m/s；最小的速度都发生在107°处，分别为-0.877 m/s、-2.117 m/s和-3.731 m/s；最大加速度发生在31.5°和128.5°处，分别为116.13 m/s2、467.11 m/s2和2 638.16 m/s2；最小加速度发生在80°处，分别为-212.72 m/s2、-717.11 m/s2和-4 028.51 m/s2。可知随着转速的增加，从动件最大速度和最大加速度越来越大；最小速度和最小加速度越来越小。

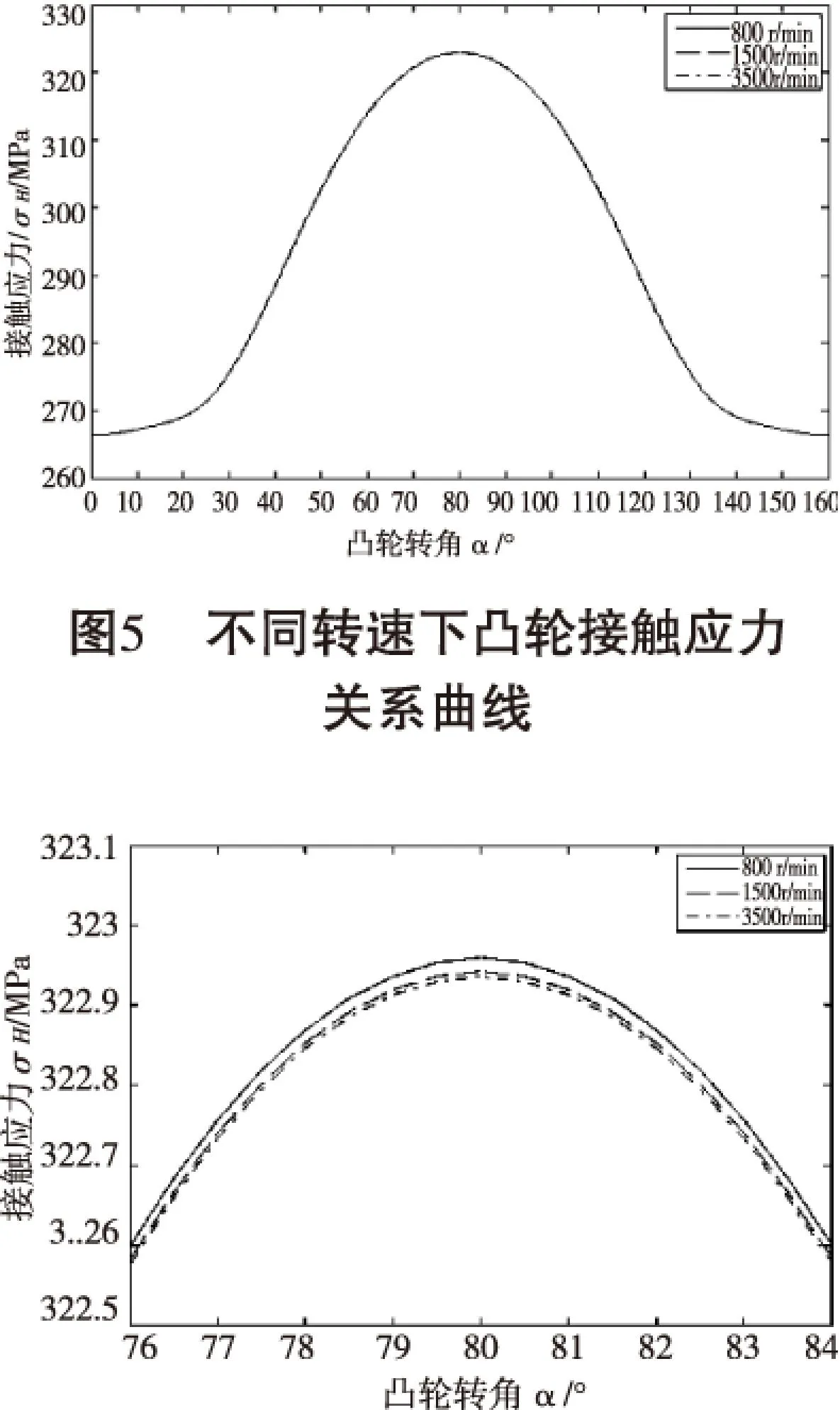
图6　最大接触应力处局部放大图

从图5和图6中可以发现，在0°和160°处，接触应力最小为266.45 MPa，因为此时凸轮所受的载荷只有弹簧的预紧力和气门组件较小的惯性力；最大接触应力发生在凸轮的桃尖处，分别为322.96 MPa、322.94MPa和322.93 MPa，可知随着转速的增加，最大接触应力有减小的趋势，但趋势并不明显。

7结论

本文通过应用MATLAB强大的数据处理功能，示例了一种配气凸轮型线设计和接触应力分析的方法，得出以下结论：

选择适当的凸轮型线函数，将预期的从动件运动参数设置为边界条件，并设置从动件的质量与刚度和不同转速参数，应用MATLAB编程，可快速生成从动件的位移和不同转速下从动件速度、加速度和凸轮接触应力曲线；通过改动设计参数值，可再次快速的完成设计计算，显著提高配气凸轮设计的速度和精度，并为凸轮机构的优化提供理论依据。

参考文献

[1]张三川. 机械原理教程[M].郑州:郑州大学出版社,2009.

[2]刘作荣. 高次多项式配气凸轮设计参数的优化[J].小型内燃机，1993，22(6):50-53.

[3]浦耿强，杨叔子，等.小型发动机配气机构接触应力分析[J].汽车科技，1999(2)6-9.

[4]尚汉冀.内燃机配气凸轮机构-设计与计算[M].上海:复旦大学出版社,1988.

[5]郭磊，褚超美，陈家祺.高次多项式凸轮型线特性参数对配气机构性能影响的研究[J].内燃机工程，2005，26(1):20-23.

[6]何振俊，李雪峰.基于MATLAB的高次多项式凸轮型线优化设计[J].机械科学与技术，2008，27(10):1141-1144.

[7]廖海平，刘启跃，陈兴，杨军. 基于MATLAB直动滚子凸轮接触应力计算[J].机械设计，2008，25(6)：49-51.

[8]罗庆生,韩宝玲.基于挤压应力条件的凸轮基圆半径的设计理论与方法[J].机械设计,2000，17(6):33-35.

[9]郭仁生.机械工程设计分析和MATLAB应用[M].北京:机械工业出版社,2012.

Profile design and contact stress analysis of automotive engine valve cam based on MATLAB

CHEN Chen，WANG Ziqin，TIAN Fengguo，CHEN Jiadui，XU Yuliang

Abstract:In the process of the profile design for automotive engine valve cam, by selecting appropriate profile function, setting the boundary conditions of expected follower motion, deriving cam contact stress formula, and then through MATLAB programming, the curves of pre-follower lift, velocity, acceleration, and the cam contact stress can be generated. The MATLAB program involved in this paper is projected to quickly complete the design and analysis of cam contact stress. Application of this method can significantly increase the speed and precision of valve cam design，and provide theoretical basis for the optimization of cam mechanism.

Keywords:valve cam; profile design; MATLAB；contact stress

收稿日期：2015-07-06

作者简介：陈晨(1990-)，男，河北邯郸人，硕士，机械设计及理论专业，主要研究方向：现代设计方法。

基金项目：贵州省科技厅贵州大学联合基金(黔科合LH字[2014]7626)。

中图分类号：TH112.2

文献标识码：A

文章编号：1002-6886(2016)01-0023-04