DT-CWT相关滤波在齿轮箱故障诊断中的应用*
2016-04-13胥永刚赵国亮侯少飞张建昌
胥永刚 , 赵国亮 , 侯少飞 , 张建昌
(1.北京工业大学先进制造技术北京市重点实验室 北京,100124) (2. 中国石油长庆油田分公司第三输油处 银川,750006)
DT-CWT相关滤波在齿轮箱故障诊断中的应用*
胥永刚1, 赵国亮1, 侯少飞1, 张建昌2
(1.北京工业大学先进制造技术北京市重点实验室 北京,100124) (2. 中国石油长庆油田分公司第三输油处 银川,750006)
根据小波系数的相关分析理论,提出了基于双树复小波变换的小波相关滤波法。该方法根据相邻层小波系数的相关性,通过迭代过程自适应地进行滤波,能够在达到良好降噪效果的同时保留微弱故障特征信息。对降噪后的信号进行希尔伯特包络分析便可准确得到故障特征频率。试验信号分析与工程应用结果表明,该方法能够有效提取强背景噪声下的齿轮箱轴承早期故障特征信息。
双树复小波变换; 相关滤波; 降噪; 齿轮箱; 早期故障诊断
引 言
齿轮箱是工业设备传动系统的重要组成部分,作为大功率动力传输设备,恶劣、复杂的工作环境使其非常容易发生故障。滚动轴承是齿轮箱的关键零部件,同时也是故障频发部件。轴承故障信号往往表现为非线性非平稳特性,并且早期故障信号常淹没于强背景噪声中,对轴承的早期故障特征提取造成了很大困难[1]。因此,对齿轮箱轴承早期故障特征信息提取方法进行研究具有重要的理论意义与工程应用价值。
小波变换通过采用与冲击信号更相近的小波函数作为基函数的方法克服了传统傅里叶基分析方法对非线性非平稳信号处理效果不佳的缺陷,已经在图像处理[2-3]及故障诊断[4]等领域有了广泛应用。双树复小波变换作为离散小波变换(discrete wavelet transform,简称 DWT)的改进方法,在继承了DWT与复小波变换优势的同时,克服了两者的缺陷,获得了近似平移不变性,具有高效的计算效率及较低的数据冗余,并且小波系数具有更好的稀疏特性[5],已经在图像处理[6]、生物医学电信号[7]及故障诊断[8-9]等领域有了成功应用。小波系数降噪方面,邱爱中[10]对双树复小波软阈值降噪方法进行了研究,并将其成功应用于水轮机轴承故障诊断。陈志新等[11]在传统阈值降噪理论的基础上提出了双树复小波块阈值降噪方法,对小波系数进行分段阈值处理,取得了良好的效果。但是,上述阈值降噪方法都是对各层小波系数独立进行阈值评估,未考虑信号突变部分在小波域形成的相邻层小波系数的局部相似现象。
笔者提出了双树复小波相关滤波方法,利用相邻层系数的相似性对小波系数进行参数自适应阈值降噪。试验模拟与工程应用结果表明,该方法能够有效地提取出强背景噪声下的微弱故障特征信息,提供了一种自适应阈值降噪方法。
1 双树复小波变换
为了克服传统离散小波变换的频率混叠,不具有平移不变性及方向选择性差等缺陷,文献[12]提出了双树复小波变换(dual-tree complex wavelet transform, 简称DT-CWT)。DT-CWT利用两组互为希尔伯特变换对的小波函数进行小波分解与重构,通过两个平行的实小波滤波器组实现,分别称为实部树与虚部树。在分解过程中要求两树小波滤波器相差半个采样间隔的延迟,从而达到实、虚部树信息互补,克服了DWT因2抽取造成的缺乏平移不变性的缺陷;与非下采样DWT相比,在获得近似平移不变性的同时极大地减少了计算冗余;滤波器构造方面比复小波变换更加容易实现[5]。
(1)
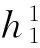
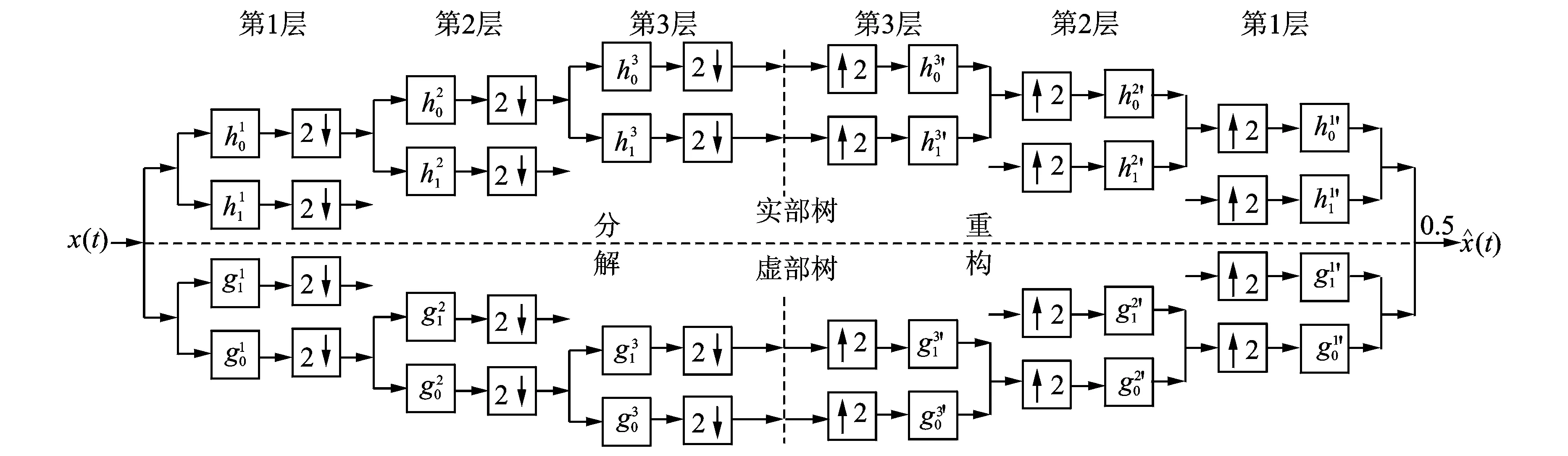
图1 双树复小波变换的分解和重构过程Fig.1 Decomposition and reconstruction process of dual-tree complex wavelet transform
2 小波相关滤波的基本原理
小波相关滤波法降噪的基本思想是,信号突变点处的小波变换结果在各层小波系数上都有较大的幅值,且变化趋势具有相似性,即冲击特征信号小波分解系数的相邻层之间存在特征相似性。此外,高斯白噪声的小波变换结果仍为高斯白噪声,且噪声变换幅值会随分解尺度的增加而快速减小。将相邻层系数进行简单地直接相乘便可以增强信号中的突变分量,同时削弱弱相关性的噪声成分。利用阈值检验便可以检出重要的突变成分,同时去除噪声,再进行重构便可以达到消噪的效果。小波相关滤波法不仅容易实现而且具有较好的鲁棒性[13]。
(2)
其中:W表示信号的小波变换系数;l表示做相关运算的小波系数的层数;m代表正在降噪的小波系数层代号;i表示做相关运算的小波分解层数变量;N代表第m层小波系数的长度。
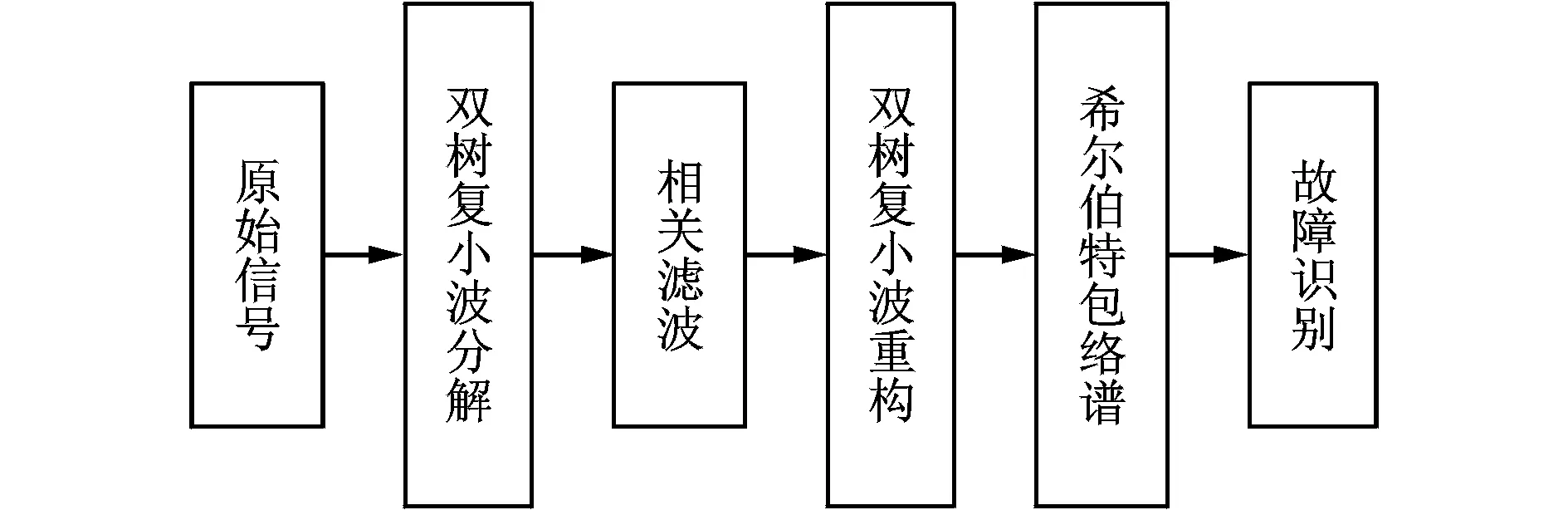
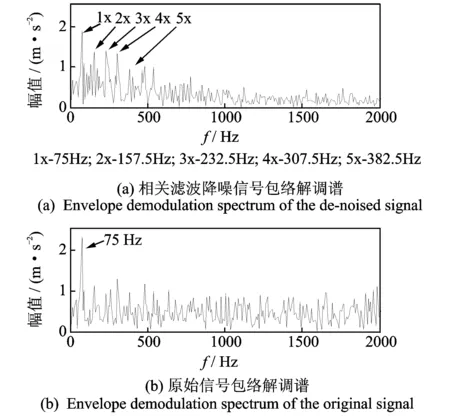
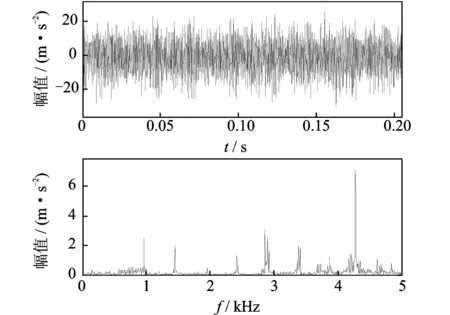
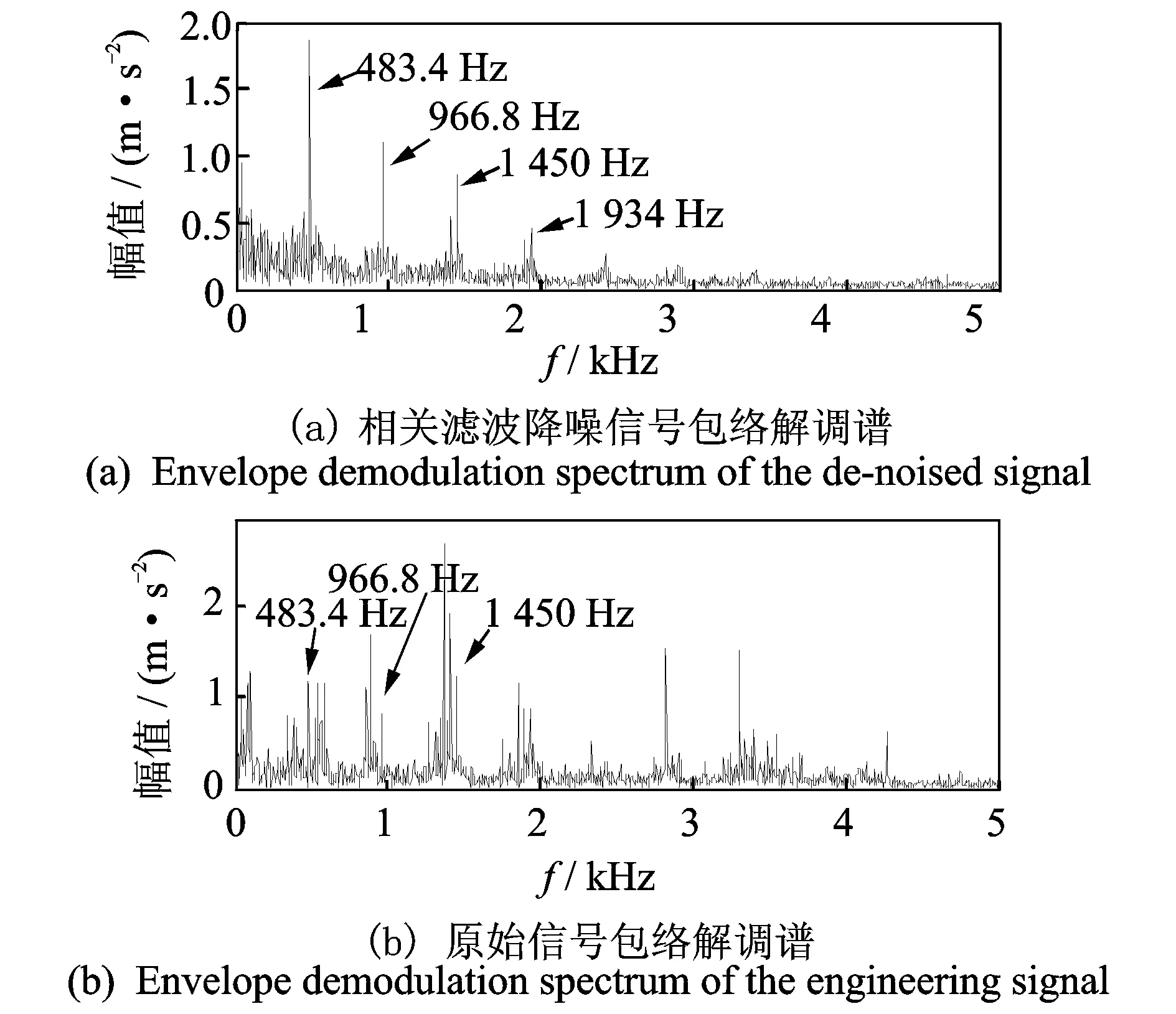
若总分解层数为M,则理论上m应该满足m 小波相关滤波的计算步骤如下。 1) 取l=2,记Wf为滤波后的小波变换系数,并进行0初始化。 (3) 归一化结果为 (4) 在某一层小波系数的处理过程中,数值比较与提取过程是一个迭代过程,直到满足步骤5的要求,即W(m,n)中剩余的小波系数能量值接近一个参考噪声为止。参考噪声的估计直接影响到算法的降噪效果。 相关滤波法在提出时首先用于图像的冗余离散小波变换中。冯辅周等[13]将其与相关排列熵相结合提出了小波相关排列熵方法并将其成功应用于轴承的早期故障诊断中。双树复小波作为传统离散小波的改进方法,获得了诸多优势;双树滤波器组信息互补充分利用了原信号的信息,平移不变性及复数形式的小波变换系数变化更为平缓,更加适合相关滤波处理。 由于小波系数的模能综合反映采样点处的突变边缘存在情况,故笔者采用双树复小波变换系数的模作为相关滤波对象,并保留相角信息以便将处理后的模还原为小波系数以便进行重构。因为参考噪声的估计直接影响降噪效果,双树复小波变换的两树滤波器组在变换过程中无数据交换,彼此相互独立,因此采用以下原则进行双树复小波相关滤波:采用文献[14]的方法对实、虚部树分别进行噪声评估,在迭代过程中当抽取剩余系数的实部与虚部序列同时满足各自的参考噪声水平后才终止迭代。基于双树复小波相关滤波的故障诊断方法流程如图2所示。 图2 基于双树复小波相关滤波的故障诊断方法Fig.2 Process of fault diagnosis method based on DT-CWT domain correlation filter 具体过程为:首先,对原始信号进行双树复小波分解,以获得各层的小波变换系数;其次,对各层小波系数按照模进行相关滤波;然后,对滤波后的系数进行双树复小波重构便可以获得降噪后的信号;最后,对降噪信号进行希尔伯特包络解调分析获得包络谱,对包络谱进行分析进而进行故障类型识别。 构建如图3所示的滚动轴承故障模拟试验系统。该系统主要包括计算机、信号调理与采集仪、压电式加速度传感器及滚动轴承实验台。轴承实验台能够模拟动平衡故障及滚动轴承的系列故障。加速度传感器安装于转子系统末端的轴承座垂直位置,测量轴承座垂直方向的振动。 图3 滚动轴承故障模拟试验系统Fig.3 Fault experiment system of rolling bearing 滚动轴承型号为6 307,轴承节径为57.5 mm,滚动体直径为13.64 mm,滚动体个数为8。通过事先在滚动轴承外圈上用线切割技术加工出宽为0.5mm,深为0.5 mm的凹槽的方法来模拟轴承外圈裂纹故障,故障轴承安装在转子系统末端。试验时电机转速为1 496 r/min,采样频率为15 360 Hz,采样点数为2 048。经计算,轴承外圈故障特征频率为76.728 Hz。信号波形及频谱如图4所示。 图4 试验信号的波形与频谱Fig.4 Waveform and amplitude spectrum of experiment signal 可见,信号波形中无明显的周期性冲击特征,频谱中边频带隐约可见,但并不明显(椭圆标示位置)。因此,并不能通过信号时域及频谱判断是否存在故障。 采用笔者提出的双树复小波相关滤波方法对该信号进行处理。先对原始信号进行5层双树复小波分解,得到各层的小波系数,各层系数的模如图5所示。图中,d1~d5分别代表分解过程中的第1~5层的小波系数。可以发现,相邻层小波系数之间存在局部相似性,但是在噪声的干扰下冲击特征并不明显。 图5 相关滤波前的各层小波系数幅值Fig.5 Coefficients amplitude of each level before correlation filter 图6为对各层系数进行相关滤波结果。可见,处理后大部分干扰成分被去除,而与相邻层存在局部相似特性的小波系数得以保留。 图6 相关滤波后的各层小波系数模Fig.6 Coefficients amplitude of each level after correlation filter 对相关滤波后的系数进行双树复小波重构便可以得到降噪后的信号,如图7(a)所示。 图7 降噪结果对比Fig.7 The noise reduction effect comparison of the experiment signal 应用双树复小波软阈值降噪(采用Donoho方法[10])方法对原始信号进行降噪处理。Donoho阈值评估公式为 (5) 采用该方法计算得到的第1~5层的阈值分别为26.27+26.55i,28.40+27.34i,26.49+28.80i,20.98+23.73i,22.63+21.08i。降噪结果如图7(b)所示。 利用dB4小波默认阈值降噪方法对原始信号进行降噪处理(计算所得的阈值为50.28),由于篇幅限制直接给出降噪结果,如图7(c)所示。 3种方法的处理效果对比可见,经双树复小波相关滤波后信号中尽管仍然存在一定程度的噪声,但周期性冲击成分与原信号相比已经比较明显;双树复小波软阈值降噪方法则将信号中的弱冲击性成分连同背景噪声一并去除;而传统dB4小波默认阈值降噪后信号完全失真。 对相关滤波后的信号进行进一步的包络解调分析,其包络解调谱如图8(a)所示。图中频率75 Hz及其倍频成分十分明显,与计算所得的故障特征76.728 Hz及其倍频非常接近,可以据此判断该轴承存在外圈故障,这与试验模拟情况相符。 图8 原始信号与相关滤波后信号的包络解调分析Fig.8 Envelope demodulation spectrum of the original signal and the de-noised signal 图8(b)为原始信号包络解调谱,虽然存在75Hz的频率成分,但是由于噪声干扰其倍频成分并不明显,影响了故障的识别。经本研究方法滤波处理后,时域与频域的故障特征均被有效提取出来。 可见,在试验模拟中双树复小波相关滤波法能够有效降低信号中的强背景噪声,将微弱故障特征信息成功提取出来,比传统的小波阈值降噪及简单的双树复小波软阈值降噪方法更加有效。 某钢铁公司高线精轧机增速箱于2006年12月底发现振动异常,开箱检查发现增速箱II轴滚动轴承外圈断裂,如图9所示,轴承型号为162250D。为了能够在故障早期发现故障并进行防范,对12月20日的振动信号进行分析。数据长度为2 048,采样频率为10 kHz,当日精轧机电机转速为1 100 r/min左右,经计算外圈故障特征频率为477.6 Hz。原始信号的波形及频谱如图10所示。可见,振动信号时域波形中没有明显的周期性冲击特征,其频谱中频率成分较为复杂,但没有发现明显的边频带,也没有发现故障特征频率。 图9 轴承外圈断裂实物图Fig.9 Picture of the bearing with outer ring broken fault 图10 工程信号波形与频谱Fig.10 Waveform and amplitude spectrum of engineering signal 对该信号分别进行双树复小波相关滤波降噪(分解层数为5)、双树复小波软阈值降噪(阈值分别为27.89+28.03i,12.52+11.86i,13.59+13.51i,6.07+6.09i,4.58+4.89i)及dB4小波默认阈值降噪(阈值为55.97)。由于篇幅限制只给出处理结果,如图11所示。 图11 工程信号降噪结果对比Fig.11 The noise reduction effect comparison of the enginerring signal 对比3种方法的降噪效果可以发现:基于双树复小波的降噪方法都具有明显的消噪效果,而传统的dB4小波默认阈值降噪方法的处理效果很不理想,处理后的信号完全失真。说明与传统离散小波变换相比,得益于其本身的优良特性,双树复小波变换具有更好的非平稳信号处理效果。 基于简单软阈值方法的双树复小波降噪方法虽然强有力地去除了噪声,但是信号中的大部分弱周期性冲击成分也被认定为噪声从而被一并去除,影响了特征提取效果。笔者提出的双树复小波相关滤波降噪方法在去除了强背景噪声的同时保留了微弱冲击成分(如图11(a)所示)。虽然降噪后的信号中仍然存在噪声并且部分特征信号也被去除了,但是信号局部的周期性冲击已经比较明显,这与相关滤波理论上能够锐化和增强信号的主要突变边缘,并压缩噪声和小的突变边缘的特性是契合的。 对相关滤波后的信号进行希尔伯特包络分析,其包络解调谱如图12(a)所示。可以发现,双树复小波相关滤波后信号的包络解调谱中频率483.4Hz 及其倍频成分十分明显,非常接近计算所得的增速箱II轴滚动轴承的外圈故障特征频率477.6 Hz,因此判断该轴承出现外圈故障。图12(b)为原始信号的包络解调谱,虽然也出现了疑似故障特征频率及其倍频成分,但是由于频率成分十分复杂,并不能确定故障类型。 图12 工程信号与相关滤波信号包络解调分析Fig.12 Envelope demodulation spectrum of the engineering signal and the de-noised signal 可见,双树复小波相关滤波法能够有效区分信号中的噪声与弱故障特征,能够在有效去除信号中的强背景噪声的同时保留微弱故障特征信息,比传统的小波阈值降噪及基于简单软阈值的双树复小波降噪方法更加有效。 1) 双树复小波采用两树互为希尔伯特变换对的滤波器组进行信号的分解与重构,更能有效地利用信号中的信息,比传统离散小波变换具有更好的非平稳信号处理效果。 2) 故障特征信号往往存在突变边缘,表现为相邻层小波变换系数间的相关性,而噪声则不存在这种相关性,可以通过相关滤波法锐化信号中的突变边缘,从而保留住信号中的冲击性突变特征。 3) 双树复小波与相关滤波相结合的方法能够有效地提取出信号中的早期微弱故障特征信息,提供了一种简单的自适应滤波方法。 [1] 丁康,朱小勇,陈亚华. 齿轮箱典型故障振动特征与诊断策略[J]. 振动与冲击,2001,20(3):7-12. Ding Kang, Zhu Xiaoyong, Chen Yahua. The vibration characteristics of typical gearbox faults and its diagnosis plan[J]. Journal of Vibration and Shock, 2001, 20(3): 7-12. (in Chinese) [2] Yu Shigong, Ahmad M O, Swamy M N S. Video denoising using motion compensated 3-d wavelet transform with integrated recursive temporal filtering[J]. Circuits and Systems for Video Technology, 2010, 20(6): 780-791. [3] Wang Zhizhong, Yong Junhai. Texture analysis and classification with linear regression model based on wavelet transform[J]. Image Processing, 2008, 17(8): 1421-1430. [4] Bouzida A, Touhami O, Ibtiouen R, et al. Fault diagnosis in industrial induction machines through discrete wavelet transform[J]. Industrial Electronics, 2011, 58(9): 4385-4395. [5] Selesnick I W, Baraniuk R G, Kingsbury N G. The dual-tree complex wavelet transform[J]. IEEE Digital Signal Processing Magazine, 2005, 22(6): 123-151. [6] Snekhalatha U, Anburajan M. Dual tree wavelet transform based watershed algorithm for image segmentation in hand radiographs of arthritis patients andclassification using BPN neural network[C]∥Information and Communication Technologies(WICT). Trivandrum:2012 World Congress on IEEE, 2012: 448-452. [7] 王芳,季忠,彭承琳. 基于双树复小波变换的心电信号去噪研究[J].仪器仪表学报,2013,34(5):1160-1166. Wang Fang, Ji Zhong, Peng Chenglin. Research on ECG signal denoising based on dual-tree complex wavelet transform[J]. Chinese Journal of Scientific Instrument, 2013, 34(5): 1160-1166. (in Chinese) [8] Seshadrinath J, Singh B, Panigrahi B K. Vibration analysis based interturn fault diagnosis in induction machines[J]. Industrial Informatics, 2014, 10(1): 340-350. [9] 胥永刚,孟志鹏,陆明,等. 基于双树复小波和奇异差分谱的齿轮故障诊断研究[J]. 振动与冲击,2014,33(1):11-16, 23. Xu Yonggang, Meng Zhipeng, Lu Ming, et al. Gear fault diagnosis based on dual-tree complex wavelet transform and singular value difference spectrum[J]. Journal of Vibration and Shock, 2014, 33(1): 11-16, 23. (in Chinese) [10]邱爱中. 对偶树复小波阈值降噪法及在机械故障诊断中的应用[J].机械传动,2011,35(9):58-61. Qiu Aizhong. A new denoising method of dt-cwt and its application in mechanical fault diagnosis[J]. Journal of Mechanical Transmission, 2011, 35(9): 58-61. (in Chinese) [11]陈志新,徐金梧,杨德斌. 基于复小波块阈值的降噪方法及其在机械故障诊断中的应用[J].机械工程学报,2007,43(6):200-204. Chen Zhixin, Xu Jinwu, Yang Debin. Denoising method of block thresholding based on DT-CWT and its application in mechanical fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2007, 43(6): 200-204. (in Chinese) [12]Kingsbury N G. The dual-tree complex wavelet transform: a new technique for shift invariance and directional filters[J]. IEEE Digital Signal Processing Workshop, 1998, 98(1): 2-5. [13]冯辅周,司爱威,饶国强,等. 基于小波相关排列熵的轴承早期故障诊断技术[J].机械工程学报,2012,48(13):73-79. Feng Fuzhou, Si Aiwei, Rao Guoqiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Journal of Mechanical Engineering, 2012, 48(13): 73-79. (in Chinese) [14]Pan Quan, Zhang Lei, Dai Guanzhong, et al. Two denoising methods by wavelet transform[J]. Signal Processing, 1999, 47(12): 3401-3406. 10.16450/j.cnki.issn.1004-6801.2016.01.023 *国家自然科学基金资助项目(51375020);北京市教委科研计划资助项目(KM201310005013);北京市属高等学校青年拔尖人才培育计划;先进制造技术北京市重点实验室开放基金;北京工业大学基础研究基金资助项目(X4001011201301) 2014-04-16;修回日期:2014-06-25 TH133.3;TH165 胥永刚,男,1975年10月生,博士、副教授。主要研究方向为机械故障诊断、现代信号处理方法等。曾发表《基于双树复小波和奇异差分谱的齿轮故障诊断研究》(《振动与冲击》2014年第33卷第1期)等论文。 E-mail: xyg@bjut.edu.cn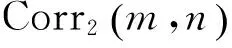

3 双树复小波相关滤波法
4 试验信号分析


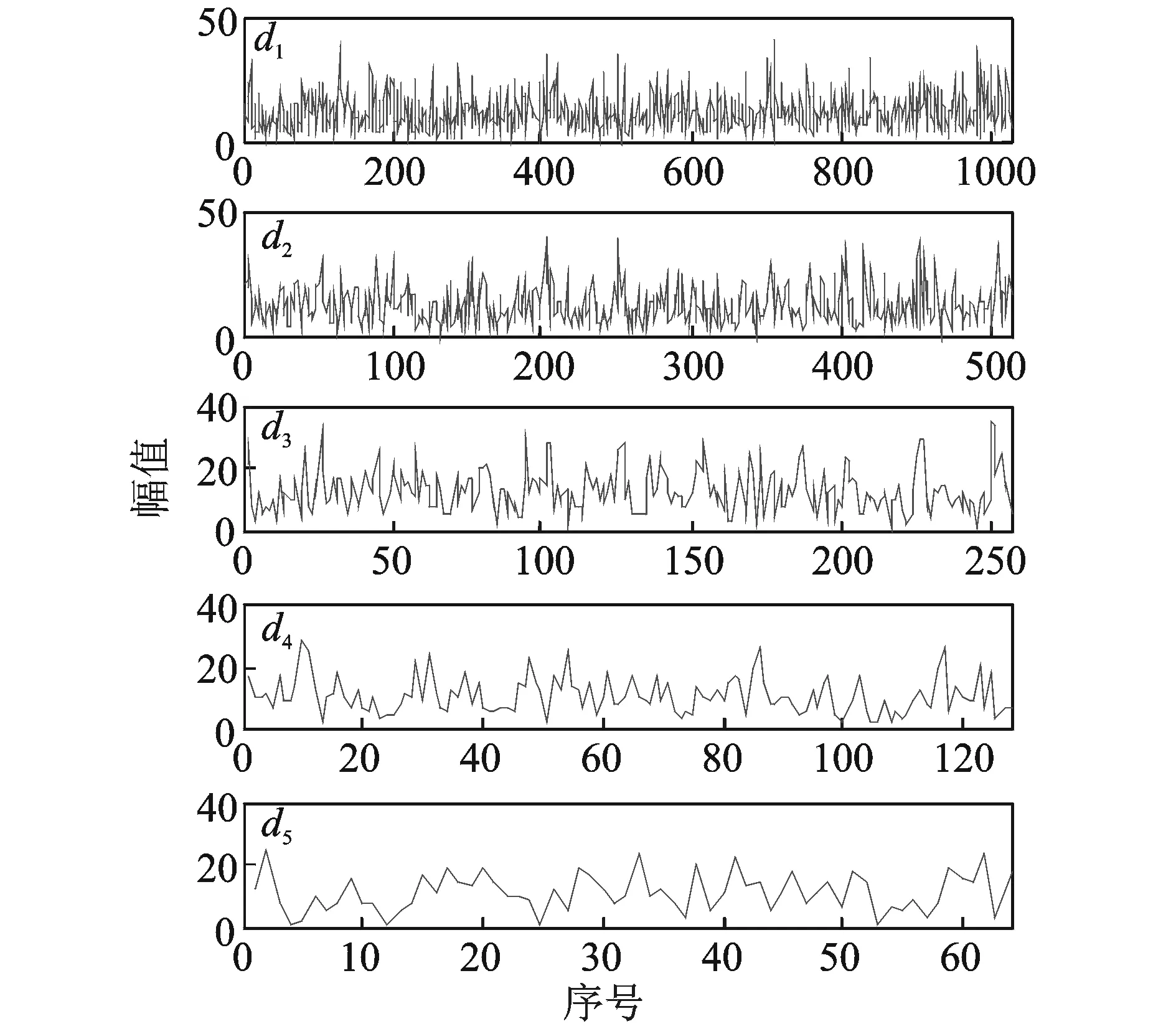
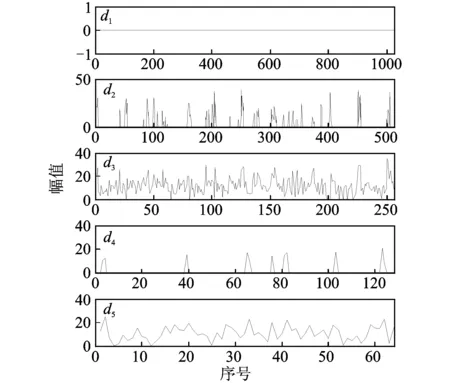
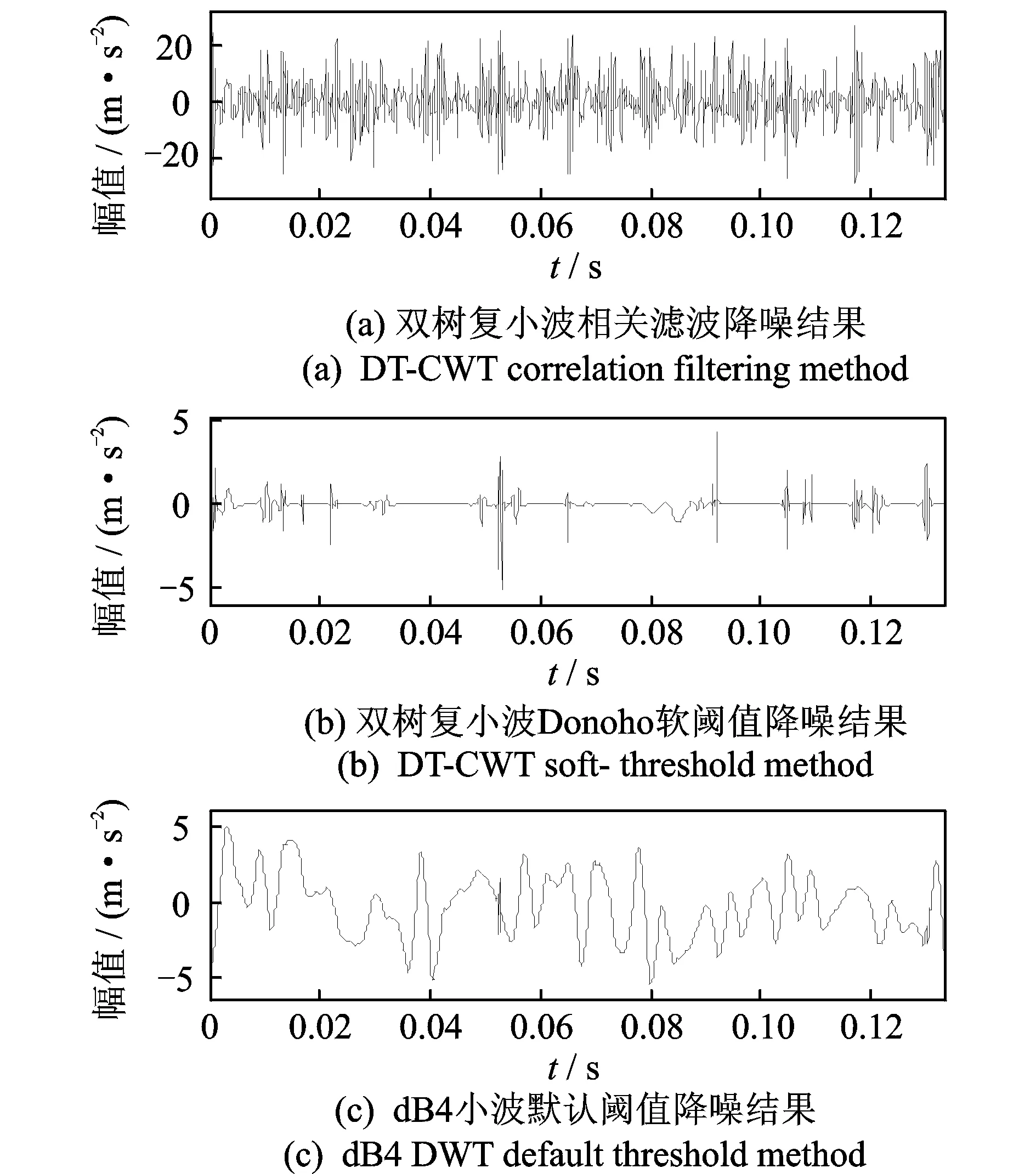
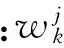
5 工程应用


6 结 论

