独立分量分析在自动机振动信号处理中的应用*

2016-04-13潘宏侠潘铭志

振动、测试与诊断 2016年1期

关键词：自动机时域分量

许昕，潘宏侠，潘铭志

(1.中北大学机械与动力工程学院太原，030051) (2.晋中学院机械学院晋中，030619)

独立分量分析在自动机振动信号处理中的应用*

许昕1，潘宏侠1，潘铭志2

(1.中北大学机械与动力工程学院太原，030051) (2.晋中学院机械学院晋中，030619)

自动机工作中的冲击响应多处在低信噪比和被噪声干扰的复杂振动信号中，寻求一种能在多干扰、噪声强的复杂振动信号中去除干扰信号和噪声的方法，可以提高速射武器自动机故障诊断准确率。研究了独立分量分析(independent component analysis,简称ICA)的基本理论，采用基于改进粒子群的独立分量分析算法模拟生成了仿真信号，获得了比较理想的分离效果。经实际射击数据验证了该方法的可行性，这种基于改进粒子群的独立分量分析算法在自动机结构振动信号处理方面具有较好的效果。

自动机；振动信号；独立分量分析；改进粒子群；信号分离

引言

自动机是速射武器的核心部件，其工作环境为高温高压高冲击，快速监测其工作的可靠性、各构件的裂纹及磨损成为速射武器领域关注的焦点。速射武器工作中机构动作复杂，采集到的振动信号往往夹杂其他部件干扰信号和环境噪声。针对这种多干扰、噪声强的复杂振动信号，需要通过现代化的测试与分析手段去除干扰信号和噪声，从而提高自动机状态监测与故障诊断的准确率[1]。

盲源分离( blind source separation，简称BSS) 是指在无法精确获知信号的理论模型和源信号的情况下，依据信号高阶统计特性从多个混合信号中分离出源信号[2]。若源信号由若干个统计上相互独立的信号组成，独立分量分析就是借助信号各分量之间的独立性同步观察交叠信号，将其分解成若干独立成分，作为对源信号的一组估计，从而实现信号的分离[3]。目前已发展出很多不同算法，但在处理非线性变化的信号时都有一定的局限性。自动机机箱内部结构复杂，在进行实射测试时振动信号在传递过程中会受到较大影响。由于机箱内部存在复杂非线性过程，使故障诊断的准确率和可靠性受到严重影响[4]。笔者通过实验证明，采用一种基于改进粒子群的独立分量分析算法可以有效解决这个问题[5]。

1 独立分量分析

改进的ICA优化算法有很多种，但都还存在一些问题，比如计算复杂、精度低、容易陷入早熟及局部收敛不足等[6-7]。笔者将一种基于动态因子及递减权重的粒子群算法(dynamic constant and inertia weight in particle swarm optimization，简称WCPSO)与非线性ICA算法结合。该算法通过动态加速常数及惯性权重的粒子群算法对目标函数进行优化，使各信号分量之间尽可能独立[8-9]。

1.1 改进的粒子群算法

提出的WCPSO数学模型为

(1)

其中：wmax，wmin为w的最小值和最大值；iter，itermax为当前迭代次数以及最大迭代次数；R1，R2，R3和R4为初始时设定的值；t，Tmax为当前进化代数以及最大进化代数。

1.2 算法改进的原理和过程

在基础ICA非线性模型中，观测信号和源信号之间的关系[10]定义

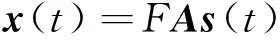
(6)

其中：x(t)为n×1维观测数据向量；F为未知可逆的非线性函数；矩阵A为n×n维混合矩阵；s(t)为由n个源信号构成的n×1维向量。

非线性模型如图1所示。

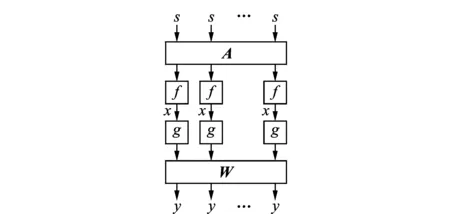
图1 ICA非线性模型Fig.1 ICA nonlinear mode

对ICA非线性模型进行参数估算时，由于在整个解的空间上存在大量的局部最优解，若直接采用梯度下降法选取，容易将最优值局限在局部最优内，此时得不到全局最优解[11]。为了避免这种情况的发生，采用互换信息量的方法来评价各分量的独立性。已知目标函数的数学模型为

(7)

按Gram-charlier级数展开求分布函数，其中H(yi)只与它的三阶和四阶累积量有关，即

(8)

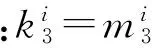
由于H(x1,x2,…,xM)与θi和W无关，目标函数的数学模型还可以表示为

(9)

如果I(y)=0，说明yi之间独立。

应用式(9)之前，首先应该把采集到的信号做白化及中心化处理，使方差为1，期望值为零。大量的实验数据证明，当把I(y)的倒数作为目标时，分离后信号的各个分量的独立性更强，得到

(10)

(11)

其中：diag(*)为取矩阵对角元素函数。

2 基于ICA的信号混叠仿真分析

为检验算法的有效性，使用以下3个源信号进行验证

随机产生一个混合矩阵A，p1为中心化及白化后的矩阵，非线性混合函数选取为

WCPSO算法中的固定粒子取20个；取R1=1，R2=0.5，R3=6，R4=2；w随迭代次数的增加由1.2逐渐减为0.4；迭代步数为100次；粒子维数n=30。

通过对图2和图4中源信号与分离后信号的对比发现，采用提出方法得到的分离效果比较理想。非线性分离函数gi(x)的参数拟合估计曲线表明，当采用高阶奇数多项式进行拟合时，非线性混合函数误差较小，这说明了该算法可以很好地对gi(x)进行估计。针对本算法将源信号和分离信号的相似系数ζij作为性能指标进行进一步验证，有

(12)

图2 原始随机信号波形Fig.2 The original signals wave

图3 混合信号波形Fig.3 The mixed signals wave

图4 分离后的源信号波形Fig.4 The source of the separated signals wave

3 实测信号分析

某定型高射机枪在实际使用中，枪机的闭锁片曾多次出现裂纹甚至折断的情况，导致机枪停射。本次实验在自动机闭锁片的两个易产生裂纹的位置预制裂纹槽：a.在闭锁片斜面圆角位置向内设置0.5 mm深的裂纹槽，左右两片对称设置；b.在闭锁片回转中心垂直于内平面的方向设置0.5 mm深的裂纹槽，左右两片对称设置，如图5，6所示，模拟出闭锁片因应力集中而产生的疲劳裂纹。

图5 故障1裂纹位置(单位：mm)Fig.5 Fault 1 crack position (unit: mm)

图6 故障2裂纹位置(单位：mm)Fig.6 Fault 2 crack position (unit: mm)

在某靶场进行了某定型高射机枪的射击实验。在机枪机匣前、中、后位置处分别设置了3个测点，选取压电式三向加速度传感器采集信号，采用三连发射击模式分别在正常状态和两种故障状态下进行了多组振动信号数据采集。

3.1 自动机振动信号时域频域图

选取三连发射击的振动信号进行分析，采样频率取51.2 kHz。在该状态下图7～9分别为正常工况和两种故障工况时三向测试信号的时域图及功率谱图。可以看出，3种不同工况下每个测点的频谱图基本相同，区别不是很明显。产生这种状况的原因是由于在真实的实验环境中，每个测点测得的信号是由许多不同的信号组成，不是单一信号。在实际环境中，自动机的故障信号其实很微弱，不容易捕捉到，这就导致3个测点采集到的信号主要是自动机本身固有的，通过这些信号识别出故障非常困难。

图7 正常工况时域图及功率谱图Fig.7 Normal working conditions time-domain form and power-spectrum form

3.2 ICA分离后时域频域图

选取三连发射击的振动信号降噪后进行分析，将3个测点的信号经过非线性ICA分解，其功率谱密度曲线如图10～12所示。可以看出，每个测点信号反映各自不同的特征。这说明应用笔者提出的算法对故障振动信号进行预处理，可以使原来比较微弱的故障特征较明显地显现出来，对后续的故障特征提取和故障模式识别工作有利。

图8 故障1信号时域图及功率谱图Fig.8 Fault 1 signals time-domain form and power-spectrum form

图9 故障2信号时域图及功率谱图Fig.9 Fault 2 signals time-domain form and power-spectrum form

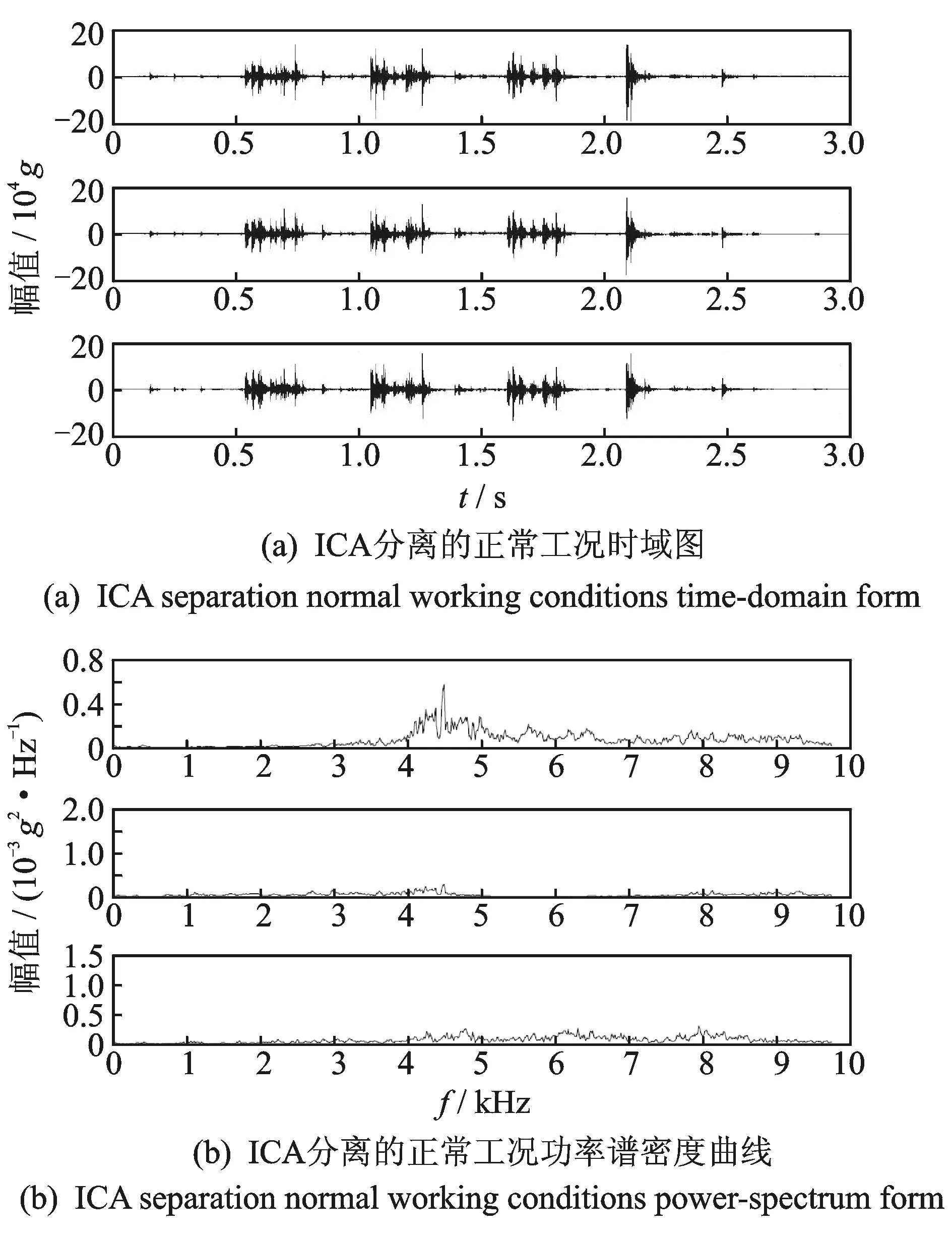
图10 ICA分离的正常工况的时域图及功率谱图Fig.10 ICA separation normal working conditions time-domain form and power-spectrum form

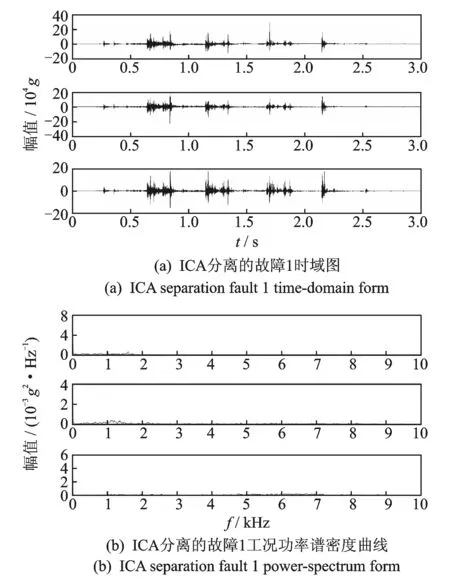
图11 ICA分离的故障1时域图及功率谱图Fig.11 ICA separation fault 1 time-domain form and power-spectrum form

图12 ICA分离的故障2时域图及功率谱图Fig.12 ICA separation fault 2 time-domain form and power-spectrum form

4 结束语

研究了ICA的基本理论，深入分析ICA系统的框架结构，采用基于改进粒子群的独立分量分析算法获得了比较理想的分离效果。模拟生成了仿真信号，利用该算法可以较好地分离出源信号，证明了该方法的可行性。经实际射击数据分析，对比降噪处理前后信号的时域频域谱特性，说明ICA可以降低信号中的噪声，提高振动信号的信噪比，可以将瞬态信号从自动机观测信号中提取出来，展示信号的特征。因此，基于改进粒子群的独立分量分析算法在自动机结构振动信号处理方面具有广阔的应用前景。

[1] 王茂林,张国平.GA35自动机机构设计创新思想分析[J].火炮发射与控制学报,2005(3):28-31.

Wang Maolin, Zhang Guoping. Analysis of innovatory thought for structure design of GA35 automatic gun [J].Journal of Gun Launch & Control,2005(3):28-31. (in Chinese)

[2] 张发启.盲信号处理及应用[M].西安:西安电子科技大学出版社，2006:1-20.

[3] 杨福生,洪波.独立分量分析的原理与应用[M].北京:清华大学出版社，2006：182-184.

[4] 闫彬,姚忠,王瑞.某火炮自动机转膛机构运动特性分析[J].火炮发射与控制学报,2010(2):31-39.

Yan Bin, Yao Zhong, Wang Rui. Movement characteristics analysis of rotary chamber mechanism of a gun automatic mechanism[J]. Journal of Gun Launch & Control,2010(2):31-39. (in Chinese)

[5] Van F den B. An analysis of particle swarm optimizers[D]. Pretoria: University of Pretoria, 2002.

[6] Aritopoulos M H, Yin H, Allison N. Image denoising using self-organizing map-based nonlinear independent component analysis[J]. Neural Networks,2002, 15(8-9): 1085-1098.

[7] Li W Q, Zhang H B, Zhao F. Independent component analysis using multilayer networks[J].IEEE Signal Processing Letters, 2007, 14(11):856-859.

[8] Sun Jun, Feng Bin, Xu Wenbo, et al. Particle swarm optimization with particles having quantum behavior[C]∥IEEE Congress on Evolutionary Computation. Portland, U.S.A:[s.n.],2004:134-138.

[9] 王丽,王晓凯.一种非线性改变惯性权重的粒子群算法[J].计算机工程与应用,2007,43(4):47-49.

Wang Li, Wang Xiaokai. A nonlinear inertia weight particle swarm algorithm[J]. Computer Engineering and Application,2007,43(4):47-49. (in Chinese)

[10]Alexander Y, Amir L, Robert P W D. Blind separation of rotating machine source: bilinear forms and convolutive mixtures [J]. Neurocomputer, ICA /BSS, 2002(SI): 349-368.

[11]Han S H, Kim H H, Bae H D. Extraction of rotating machine sources for fault diagnostics using independent component analysis [C]∥IEEE Instrumentation and Measurement Technology Conference. Ottawa, Ontario, Canada: [s.n.], 2005:1507-1512.