基于PSO-BP与组合矩的水电机组轴心轨迹识别*
2016-04-13陈喜阳闫海桥孙建平
陈喜阳, 闫海桥, 孙建平
(华中科技大学能源与动力工程学院 武汉,430074)
基于PSO-BP与组合矩的水电机组轴心轨迹识别*
陈喜阳, 闫海桥, 孙建平
(华中科技大学能源与动力工程学院 武汉,430074)
引入了一种由Hu矩和仿射矩构成的组合不变矩作为水电机组轴心轨迹的反向传播(back propagation,简称BP)自识别神经网络的输入特征向量,在粒子群优化算法(particle swarm optimization, 简称PSO)的基础上,融入粒子位置越界处理和全局最优位置未更新计数器,利用改进的粒子群算法求解BP网络连接权值,水电机组轴心轨迹的BP识别速度和精度得以显著提升,采用优化思想对初步识别结果进行量化分析,提取定量的轴心轨迹形状特征参数,可为水电机组故障定位提供指南。仿真实验和应用实例表明,组合不变矩的识别方法优于Hu矩或仿射矩方法,构建的PSO-BP具备较高的收敛速度和识别精度,所提出的轴心轨迹识别方法成功应用到了水电机组动不平衡故障诊断案例。
组合矩; 粒子群优化算法; BP神经网络; 水电机组; 轴心轨迹; 识别
引 言
《能源发展“十二五”规划》明确提出“应积极有序发展水电等可再生能源”, 水电作为一种可再生的清洁能源,已成为我国安全、稳定、经济和清洁的现代能源产业体系的重要组成部分。水电机组在运行过程中常受到水力、机械和电气3方面耦合影响,导致机组稳定性下降,若不及时诊断和检修,可能引发灾难性事故。轴心轨迹作为水电机组运行状态或故障征兆的信息载体,其形态反映了转子瞬态运行状况,包含了丰富的故障征兆信息[1]:椭圆形体现了转子不平衡;外“8”字形预示了不对中;花瓣形标志了动静件碰摩;纽扣形表示油膜涡动等。
轴心轨迹已成为水电机组运行性能分析及故障诊断系统中重要征兆量,其轨迹特征提取和高效识别技术近年来受到行业内广泛关注。文献[2]利用奇异特征值作为特征向量, 采取最邻近法对水电机组轴心轨迹的自动识别进行研究。文献[3]提取轴心轨迹多重分形谱特征,利用模糊C-均值聚类法对特征进行聚类识别。文献[4]利用奇异性指数的统计量特征,可以有效区分不同类型的故障的轴心轨迹。文献[5]采用小波包特征熵作为轴心轨迹征兆量。文献[1,6-8] 计算Hu矩作为轴心轨迹特征向量,基于BP神经网络、灰色理论的关联度分析、SVM分类识别。文献[9]通过仿真和工程实例验证了不变矩特征对混沌振子相图状态识别具有较强的抗噪性能和识别能力。文献[10]实现了基于Zernike不变矩特征和BP神经网络的轴心轨迹自动识别方法。文献[11-12]将仿射不变矩应用于图形的模式识别中并得到较好的识别效果。文献[13-14] 提出基于仿射不变矩和BP神经网络的轴心轨迹分类。国内外已进行的工作主要是结合连续不变矩(或离散不变矩)提取轴心轨迹特征,采用神经网络进行自动分类识别并取得了一定效果。
笔者在信息融合理论基础上,引入一种由改进的Hu矩和仿射矩构成的组合不变矩,作为描述水电机组轴心轨迹的特征量,采用改进的粒子群算法训练BP的权值,提高BP网络的收敛速度和抗局部最优能力,构建PSO-BP对轴心轨迹高效识别,通过优化策略对分类结果做定量分析,提取轴心轨迹形状的量化特征,并成功应用于水电机组动不平衡故障的配重应用实例。
1 轴心轨迹组合不变矩构造
水电机组运行工况复杂,轴心轨迹轮廓线在大多数情况下并非完全封闭的曲线。若直接采用连续平面矩求解轨迹曲线特征,需要判断轴心轨迹进动方向且需对轨迹曲线着色填充,求解过程比较复杂[1]。由于传统离散点不变矩仅满足平移不变性和旋转不变性,不满足比例因子缩放不变性,无法精确描述轴心轨迹形状特征,易造成轨迹形状误判。工程人员通常采用归一化处理技术构建改进的离散型曲线不变矩,用来提取轴心轨迹特征。文献[6]构造的新Hu矩如式(1)所示,并采取对数的方式缩小新Hu矩变化范围

(1)
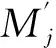
文献[14]采用归一化策略,消除比例因子的影响,构造的新仿射矩为

考虑Hu矩作为图像征兆量识别时相对速度较快,但不具备仿射不变形,容易降低目标识别率,而仿射矩具备仿射不变性,在观测目标的角度不同时具有较好的稳定性。为了更加全面地捕获水电机组轴心轨迹轮廓形状的描述特征信息,笔者基于信息融合思想,充分利用 Hu矩和仿射矩的不同特点,将两者组合成描述水电机组轴心轨迹图像的多源信息载体,构造了一种组合不变矩作为轴心轨迹特征量,高效捕捉轴心轨迹图像特征。
2 PSO-BP的轴心轨迹识别
2.1PSO-BP算法
BP由输入层、隐含层和输出层组成,以连接权值矩阵为变量,误差函数为求解目标的多元极小值问题,通过样本进行训练,确定网络神经元之间的连接权值和阈值,实现从输入空间到输出空间的映射关系,构成分类识别系统。BP采纳了梯度法,虽然可逼近任何非线性函数,但在实际工程应用过程中,BP算法普遍存在收敛速度慢和局部最小问题[1]。研究人员尝试了不同方式对BP网络进行优化,取得了一定的成果,粒子群优化算法就是其中应用比较好的一种算法,可采用PSO展开对BP网络中神经元之间的连接权值寻优。
粒子群优化算法源于对鸟群捕食行为模拟的进化算法,采用智能群体思想,依靠个体协作来执行多维寻优。PSO优化BP网络主要是将神经元之间的连接权值表征为粒子,迭代计算各个粒子的适应度值,比较后一代与前一代的适应度值来更新粒子个体最优位置以及全体粒子的全局最优位置,预设目标误差以及迭代次数来控制迭代循环,PSO迭代后的结果直接作为BP网络的初始权值,然后再进行BP网络训练,加快BP网络收敛速度,提高寻优和避免局部最优能力。参照文献[15],引入粒子位置越界处理和全局最优位置未更新计数器,提高标准PSO算法的对神经元连接权值寻优的收敛速度和全局寻优能力,PSO-BP算法流程如下。
1) 初始化BP网络结构,确定输入层、隐含层和输出层的神经元个数,传递函数、学习率、动量因子、样本学习的目标误差和最大迭代次数等参数。
2) 初始化PSO,将BP神经元的连接权值表征为粒子。初始化粒子规模,搜索空间目标维数,学习因子c1和c2,惯性权值ωmax和ωmin,速度vmax和vmin,搜索范围Xmax和Xmin,目标精度、最大迭代次数、全局最优位置未更新计数器门槛值等。
3) 计算每个粒子的适应度值,若小于粒子自身历史最优适应度值pbest,则更新pbest,否则pbest维持不变。
4) 将全体粒子中的最小适应度值与全局最优适应度值gbest进行比较,若小于gbest,则更新gbest,否则gbest维持不变。
5) 更新粒子的速度以及位置。改进PSO的措施[15]:判断全局最优位置未更新计数器是否达到预设门槛值,若达到门槛值,则对该粒子初始化,提高其摆脱局部最优的活力;采用镜像映射减少在边界周围粒子的扎堆现象,提高粒子种群的寻优速度和全局搜索能力。
6) 判断是否达到预设迭代次数或者目标精度,若不满足条件,则返回步骤3,否则输出粒子的gbest。
7)gbest作为BP神经元的连接权值的初始值,展开BP网络样本学习训练。
8) 判断是否达到迭代次数或者样本训练目标误差值,完成BP神经网络学习过程,若误差在设定范围内,该BP神经网络可应用于模式识别。
2.2 仿真算例
在Matlab7.5(R2007)环境下,通过仿真产生水电机组4种常见故障的轴心轨迹:椭圆、纽扣、外8字和花瓣(一般分别对应于动不平衡、油膜涡动、不对中和动静碰摩故障)。训练样本的参考轴心轨迹如图1所示。待识别的轴心轨迹如图2所示。
按照轴心轨迹组合不变矩提取策略,分别计算图1,2中轴心轨迹的Hu矩、仿射矩和组合不变矩,如表1和表2所示。
建立BP神经网络对轴心轨迹识别,隐含层节点为17,输出层节点为3(神经网络输出编码:纽扣(1 0 0)、椭圆(0 1 0)、外8字(0 0 1)、花瓣形(1 1 0)),输入层节点为特征量维数(轴心轨迹特征量为组合不变矩、Hu矩和仿射矩时,对应的输入层节点分别为8,6和2),传递函数为logsig,训练函数为traingdm,学习率lr=0.3,动量因子mc=0.3,训练误差goal=0.000 5,最大训练步数为10 000。选用Hu矩、仿射矩或组合不变矩作为轴心轨迹特征量,评价3种方案在神经网络识别中的有效性。
为了比较PSO-BP和BP在收敛速度和抗局部最优的能力,选择组合不变矩作为轴心轨迹特征向量,通过PSO展开对BP网络中神经元的连接权智能寻优,改善BP性能。PSO参数设置为:粒子群个数N=30,最小惯性系数ωmin=0.5,最大惯性系数ωmax=0.85,学习因子c1=c2=2,最大迭代次数为1 000,最大速度vmax=1,最小速度vmin=-1,最大位置Xmax=10,最小位置Xmin=-10,全局最优位置未更新计数器门槛为100。 选择参考轴心轨迹作训练样本,待识别轴心轨迹的辨识结果如表3所示。Hu矩和BP、仿射矩和BP、组合矩和BP识别方案中训练迭代次数都达到10 000步,最终均未达到设定的误差值。组合矩和PSO-BP的迭代步数为316步,达到了预设误差值。

图1 参考轴心轨迹Fig.1 Reference axis orbit
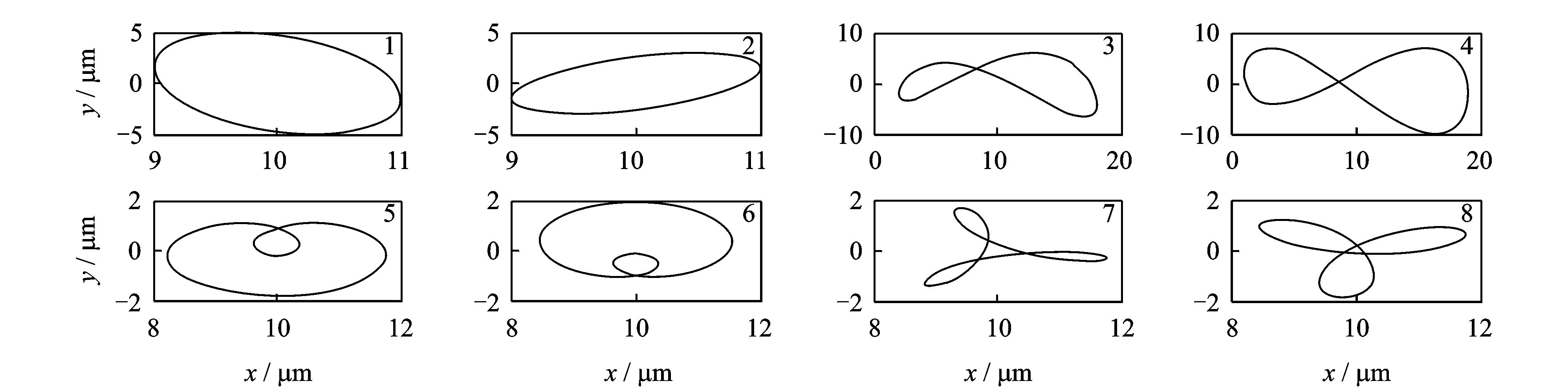
图2 待识别的轴心轨迹Fig.2 The axis orbits to be identified
由待识别轴心轨迹的识别结果,可知:
表1 参考轴心轨迹的不变矩数值表
Tab.1 The moment invariants list of reference axis orbits

轴心轨迹类型组合不变矩Hu矩仿射矩M1M2M3M4M5M6F1F2纽扣11.26492.98352.04054.55254.23156.78680.0261-2.2821纽扣21.73943.68981.93994.75484.13576.9427-0.3467-1.9182纽扣31.65513.90042.18425.95693.80705.23410.0209-1.3860纽扣41.72823.47942.17065.63803.33405.0072-0.0808-2.2458椭圆11.05577.08257.082514.165012.169925.038426.064821.3038椭圆20.62427.16167.161614.32339.739924.753225.642520.9943椭圆30.27307.30987.309814.61969.792625.165125.446120.8265椭圆40.20008.11318.113116.22639.818225.377925.179920.5043外8字10.81902.84422.93995.83203.45737.9189-0.22740.6221外8字20.81042.33763.65877.24294.35126.6720-0.03101.0351外8字30.82942.31993.40356.82613.90326.28230.07771.1427外8字40.51932.34523.86067.87823.95856.9668-0.15660.9006花瓣18.63971.206611.481617.83256.731518.5802-1.40530.2005花瓣25.60161.20666.656910.61214.948411.0836-1.41960.1924花瓣33.26941.32414.60968.19393.82567.5895-1.30370.2520花瓣42.41271.41393.98947.30853.45666.7041-1.21790.2942

表2 待识别轴心轨迹的不变矩数值表

表3 待识别轴心轨迹的神经网络输出结果
1) Hu矩和BP、仿射矩和BP、组合矩和BP、组合矩和PSO-BP 4种模式对轴心轨迹的识别率都达到100%。
2) 计算各模式中神经网络输出与期望目标值的最大误差,Hu矩和BP为6.34%、仿射矩和BP为14.5%、组合矩和BP为3.79%、组合矩和PSO-BP为3.94%。组合不变矩对轴心轨迹的识别更为精准,优于采用Hu矩或仿射矩作为特征向量的方式,验证组合不变矩是一种有效的描述轴心轨迹的特征量。
3) PSO应用到BP神经元间的权值寻优,收敛步数从10 000降低到316次,加快了收敛速度,提高寻优和避免局部最优能力,达到了预设目标误差值。这证明了引入粒子位置越界处理和全局最优位置未更新计数器构建的PSO-BP网络是一种高效精准的轴心轨迹识别方案。
3 应用实例
在水电机组在线监测或试验应用中,通过大轴各导轴承截面布置正交的电涡流位移传感器合成轴心轨迹,可用于判别机组运行性能和故障类型。结合某水电站,给出笔者提出方法在动不平衡故障案例中的实际应用,该电站机组参数为:型号为HLA606-LJ-122;额定水头为96 m,最大净水头为100 m,最小净水头为90 m;额定流量为10.71 m3/s;额定出力为93.26 kW;额定转速为600 r/min;转子起吊重量为33 t。
配重前测点振动如表4所示,根据国标CB/T 11348.5—2002关于旋转机械转轴径向振动的测量和评定可知,摆度值位于A区,属于可以长期运行的范围之内。根据国标CB/T 6075.5—2002关于在非旋转部件上测量和评价机器的机械振动可知,上机架振动值偏大,因此以减小上机架振动为主要目的。空励实验结果表明,机组的磁拉力较小可以在配重时不考虑磁拉力的影响。下导轴心轨迹如图3中的通频轴心轨迹图(配重前),提取原始轴心轨迹的1倍转频、2倍转频、3倍转频和4倍转频,合成转频轴心轨迹图(配重前)。
配重前1~4倍转频轴心轨迹的组合不变矩为{1.283 5,8.283 3,8.283 3,16.566 6,9.353 3,25.945 7,22.586 9,18.528 2},经PSO-BP识别为椭圆形,说明该机组存在着动不平衡故障,有望借助于配重缓解机组振动程度。传统的轴心轨迹形状识别仅是定性的初步认知,这里可采用优化的思想,进一步捕捉轴心轨迹的定量信息, 为故障诊断提供更加详细的指南。以辨识的椭圆形状轴心轨迹为例,设椭圆标准方程为
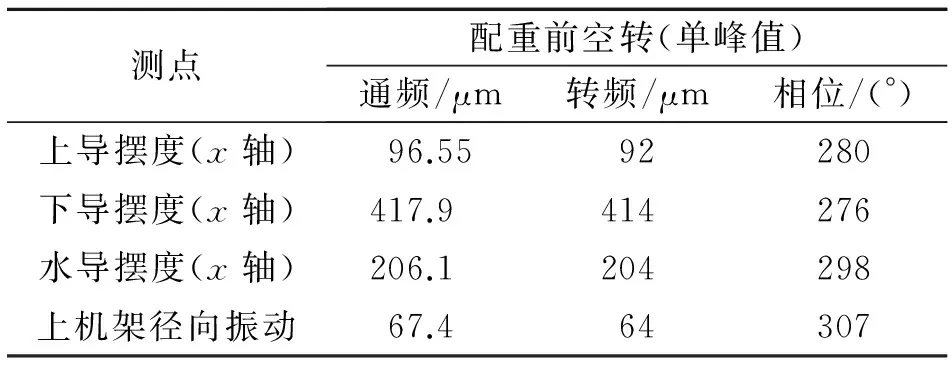
表4 配重前振动数据列表

(3)
经旋转ψ和平移(ΔmΔn)后的椭圆方程为

(4)
建立优化问题模型为
(5)

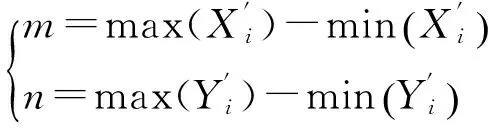
通过拟合椭圆的量化参数,如旋转角度判断动不平衡位置,可确定配重方位,为排除故障提供帮助。针对配重前1~4倍转频椭圆形的轴心轨迹,通过优化计算可得长轴半径为607.312 6 μm,短轴半径为446.263 7 μm,旋转角度为-89.019 5°,即动不平衡失重角为-89.019 5°,逆时针旋转180°,得配重角度为90.98°,现场最终配重位置取笛卡尔坐标角度89°,配重大小则由式(6)试配后,最终确定为10 kg。
(6)
其中:m0为试配质量(kg);G为转子质量(kg);u0为机组未配重时的最大振幅(μm);R为试配重半径(m);n为机组额定转速(r/min)。
配重后的测点振动数据如表5所示。可以看到,上导摆度的转频分量单峰值减小了71 μm,下导摆度的转频分量单峰值减小了147 μm,水导摆度的转频分量单峰值减小了57 μm,上机架径向振动分量单峰值减小了54 μm,楼板已经没有明显振动感觉,缓解了机组动不平衡故障,配重效果显著。
水电机组的振动多数是由于发电机转子的质量不平衡造成的。轴心轨迹识别的应用实例再次证明了组合不变矩是一种有效的轴心轨迹特征向量,构建PSO-BP具备较高的轴心轨迹识别能力,通过提取轴心形状的量化特征可为实际查找水电机组故障原因提供指南。
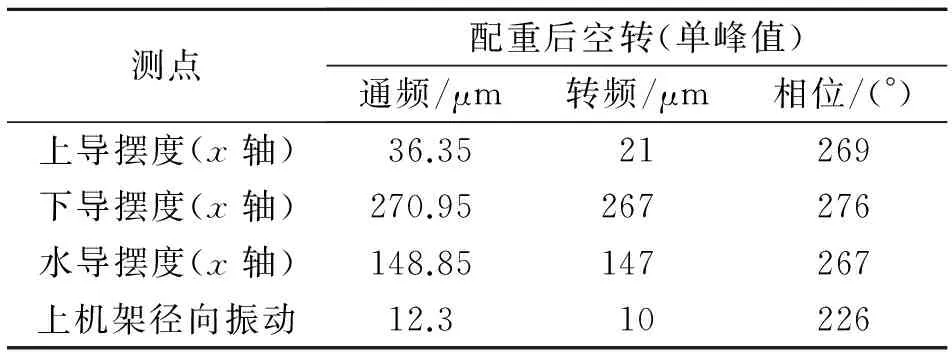
表5 配重后振动数据列表
4 结束语
构造了一种由改进的Hu矩和仿射矩构成的组合不变矩作为描述水电机组轴心轨迹形状的特征向量。仿真实验证明,组合不变矩比Hu矩或仿射矩更能表征轴心轨迹形态特征。采用改进的PSO来训练BP的权值,提高了收敛速度和抗局部最优能力,构建的PSO-BP具备高效的轴心轨迹识别效果。通过优化思想对PSO-BP轴心轨迹识别结果做进一步的定量分析,提取量化的形状参数为查找故障位置提供指南,并成功应用于某电站动不平衡故障实例,取得了较好配重效果。
[1] 陈喜阳.水电机组稳定性监测中状态分析方法研究[R].南京:南京南瑞集团,2008.
[2] 倪传坤,周建中.基于SVD的水电机组轴心轨迹自动识别[J].水电自动化与大坝监测,2003,27(6):22-24.
Ni Chuankun, Zhou Jianzhong. SVD-Based automatic identification of axis track of hydropower generating sets[J]. Hydropower Automation and Dam Monitoring, 2003,27(6):22-24. (in Chinese)
[3] 李辉,白亮,罗兴錡,等.基于模糊聚类的水电机组轴心轨迹多重分形特征识别[J].水力发电学报,2012,31(4):238-242.
Li Hui, Bai Liang, Luo Xingqi, et al. Multi-fractal feature recognition for shaft centerline orbit of hydropower units based on fuzzy clustering[J]. Journal of Hydroelectric Engineering, 2012,31(4):238-242. (in Chinese)
[4] 申弢,黄树红,张燕平,等.振动故障信号奇异性指数的统计特征研究[J].振动工程学报,2003,16(4):476-479.
Shen Tao, Huang Shuhong, Zhang Yanping,et al.Studies on statistical features of singularity of faulty vibration signals[J]. Journal of Vibration Engineering, 2003,16(4):476-479. (in Chinese)
[5] 桂中华,潘罗平,张浩,等.小波包特征熵提取水电机组轴心轨迹形状[J].水力发电,2009,35(8):49-51.
Gui Zhonghua, Pan Luoping, Zhang Hao, et al. Extracting axis orbit of hydro - generating unit using characteristic entropy of wavelet packet[J]. Water Power, 2009, 35(8): 49-51. (in Chinese)
[6] 陈喜阳,张克危.一种新矩在水电机组轴心轨迹识别中的应用[J].华中科技大学学报:自然科学版,2006,34(3):79-81.
Chen Xiyang, Zhang Kewei. Application of a new moment invariant to identification of axis orbit in hydro-generator unit[J]. Huazhong University of Science & Technology: Nature Science Edition, 2006,34(3):79-81. (in Chinese)
[7] 李友平,陈启卷.基于灰色理论与不变性矩的水电机组轴心轨迹自动识别[J].电力系统自动化,2001,25(9):19-21.
Li Youping, Chen Qijuan. Automatic identification of axis orbit of hydroelectric generation set based on grey theory and moment invariants[J]. Automation of Electric Power Systems, 2001,25(9):19-21. (in Chinese)
[8] 祝晓燕,常宏飞,朱霄珣,等.基于SVM与轴心轨迹不变矩的转子状态识别方法[J].汽轮机技术,2012,54(6):469-472.
Zhu Xiaoyan, Chang Hongfei, Zhu Xiaoxun, et al. A method in support vector machines based invariant moments to recognize shaft orbit[J]. Turbine Technology, 2012,54(6):469-472. (in Chinese)
[9] 胥永刚,马海龙,冯明时,等.基于不变矩的微弱信号检测方法[J].振动、测试与诊断,2012,32(4):568-571.
Xu Yonggang, Ma Hailong, Feng Mingshi, et al. New method for weak signal detection based on invariant moment[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(4):568-571. (in Chinese)
[10]许飞云,钟秉林,黄仁.轴心轨迹自动识别及其在旋机诊断中的应用[J].振动、测试与诊断,2009,29(2):141-145.
Xu Feiyun, Zhong Binglin, Huang Ren. Automatic recognition of shaft orbit and its application to fault diagnosis of rotation machinery[J]. Journal of Vibration, Measurement & Diagnosis, 2009(2):141-145. (in Chinese)
[11]Tomas Sulk, Jan Flusser. Affine moment invariants generated by graph method[J]. Pattern Recognition, 2011(44):2047-2056.
[12]Hosny K M. On the computational aspects of affine moment invariants for gray-scale images[J]. Applied Mathematics and Computation, 2008(195):762-771.
[13]付波,周建中,彭兵,等.基于仿射不变矩的轴心轨迹自动识别方法[J].华中科技大学学报:自然科学版,2007,35(3):119-121.
Fu Bo, Zhou Jianzhong, Peng Bing, et al. Auto-recognition of shaft orbits using affine moment invariants[J]. Huazhong University of Science & Technology: Nature Science Edition, 2007,35(3):119-121. (in Chinese)
[14]周训强.旋转机械轴心轨迹的提纯、特征提取与自动识别研究[D].重庆:重庆大学, 2010.
[15]周程,张培林.基于改进PSO的均衡性视角铁矿石运输-分配模型研究[J].计算机应用研究,2013,30(5):1388-1392.
Zhou Cheng, Zhang Peilin. Research on ore transport-distribution model based on equilibrium perspective and improved PSO[J]. Application Research of Computers, 2013, 30(5):1388-1392. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2016.01.018
*中央高校基本科研业务费专项资金资助项目;华中科技大学自主创新研究基金资助项目(0118120050)
2014-03-14;修回日期:2014-05-05
TH133; TP277
陈喜阳,男,1976年12月生,讲师。主要研究方向为水电机组在线监测及故障诊断、水电厂状态检修。曾发表《一种新矩在水电机组轴心轨迹识别中的应用》(《华中科技大学学报:自然科学版》2006年第34卷第3期)等论文。 E-mail:chenxiyang@mail.hust.edu.cn
