供电电源包含谐波及不平衡共存时感应电机损耗特性*

张冬冬， 赵海森， 赵伟波， 王莎莎， 白志军

(1. 华北电力大学 新能源电力系统国家重点实验室，北京 102206； 2. 国网甘肃刘家峡水电厂，甘肃 永靖 731600)

供电电源包含谐波及不平衡共存时感应电机损耗特性*

张冬冬1， 赵海森1， 赵伟波1， 王莎莎1， 白志军2

(1. 华北电力大学 新能源电力系统国家重点实验室，北京 102206； 2. 国网甘肃刘家峡水电厂，甘肃 永靖 731600)

受系统中电源多样化及非线性负荷的影响，用户侧电源中会出现包含谐波及不平衡共存现象。当电动机运行在此类复杂电源质量条件下，会造成能效降低、温升增加，严重情况下会导致电机损坏，影响安全生产。为了研究供电电源包含谐波及不平衡共存时感应电机损耗特性，以一台5.5kW笼型感应电机为例，设计了9种电源包含谐波及不平衡共存时的供电电源波形，进一步利用时步有限元法，分析了在上述不同供电电源波形情况下，电机内部定转子铁心磁密及转子导条电流密度的分布特点，并进一步分析了空载及负载情况下的损耗特性；最后通过试验验证了文中分析结果的正确性。

谐波； 电源不平衡； 时步有限元； 损耗

0 引 言

随着半导体技术的发展，现代电力系统的电力电子设备应用日益广泛。根据相关调查，在1992年以电力电子设备为主的非线性负荷占总负荷量的15%～20%，而现在这一比例为 50%～70%[1]，将使电网不可避免地含有大量的谐波成分。另外，由于配电网的电压不平衡以及大部分的家用电器多为单相负荷，不可避免地造成电网三相电压不平衡。因此，电网电压不可避免的同时出现三相电压不平衡且含有大量的谐波。当电机运行在此工况下时，会产生三相电流不平衡、附加损耗增加、温升过高、输出转矩减小、脉振转矩及振动噪声大等不良影响[2-3]。为了探索供电电源包含不平衡和谐波条件下，感应电机安全运行及节能控制策略，有必要对电压不平衡度和谐波畸变率复杂组合状况下感应电机的运行和损耗性能进行研究。

在单独电压谐波畸变和不平衡度方面已有大量文献开展了相关研究。电压不平衡对感应电机运行及损耗性能影响方面，文献[4]利用复数电压不平衡度同时将幅值和相角不平衡因素包含在内，分析了电压相角不平衡对感应电机运行性能的影响，最终提出在分析感应电机不平衡运行问题时必须考虑电压相角对其的影响；文献[5]对电压不平衡条件下感应电机的损耗、温升、噪声、振动、转矩脉动、转差率、轴电压、轴电流和加速转矩进行了分析，并指出电压不平衡导致转子损耗增加；文献[6]利用对称分量法得到： 综合IEC中电压不平衡度定义与电压不平衡情况可以精确地评估电压不平衡对感应电机总铜耗、输入功率、功率因数及总输出转矩的影响程度，但同时也要考虑电压相角对三相绕组最大电流及降额因数的影响，并引入衡量电压不平衡状况的系数，它有助于对电压不平衡条件下感应电机的运行性能进行更为准确的评估。在电压波形含有谐波对感应电机运行性能及损耗影响方面，也有大量文献开展了相关研究。例如，由于变频电源含有大量的谐波，为了分析谐波对铁耗的影响，文献[7]提出了一种由PWM逆变器供电的感应电机的铁耗计算方法。文献[8]研究了由逆变器供电的电机系统中电网侧的谐波成分与电机自身结构产生的谐波成分的相互作用现象，并指出当电机内部谐波成分接近于电网侧的共振谐波成分时，将在电机和电网中产生大量的附加损耗，并且电机脉振转矩将大大加强。文献[9]提出一种利用时步有限元计算感应电机铁耗的新方法，并证明要准确地计算感应电机铁耗必须要考虑供电电源谐波分量的初相位。

但是，很少有文献考虑过当供电电源包含谐波及不平衡共存时的感应电机损耗特性。另外，以往大部分研究主要针对电机总损耗进行分析，在单独某项损耗随电压不平衡度、谐波畸变率变化的规律方面的研究不够全面。针对以上问题，本文利用时步有限元从电机内部磁场分布特点出发，系统分析了损耗；并针对一台Y132S-4—5.5kW感应电机，建立基于多截面场-路耦合时步有限元的损耗计算模型，研究了电压不平衡度及谐波畸变率共存时电机内部电磁场及各项损耗的影响。最后，指出本文研究意义在于对传统电机能耗理论的完善，为电能质量偏差条件下电机系统节能新途径研究提供重要技术支持。

1 供电电源包含谐波及不平衡共存现象和有限元分析模型

1.1 包含谐波及不平衡共存的电源波形

在单相非线性负荷(如家用荧光灯、电弧焊和电焊机等)大量应用的区域，电压不平衡与谐波往往共存，并且这种现象是常见的。一般情况下，电网电压的不平衡度符合国家标准，即不平衡度小于5%。当电机由逆变器供电时，根据逆变器的性能和工作条件不同，电压谐波含量一般较大。因此，为了使研究更加有现实意义，本文选取由不平衡度为0%、3%、5%，谐波含量为10%、15%、20%组成的9种电源电压组合情况，各种组合情况如表1所示。本文分别对感应电机满载和空载情况，进行仿真计算。各种组合的电压波形如图1所示。

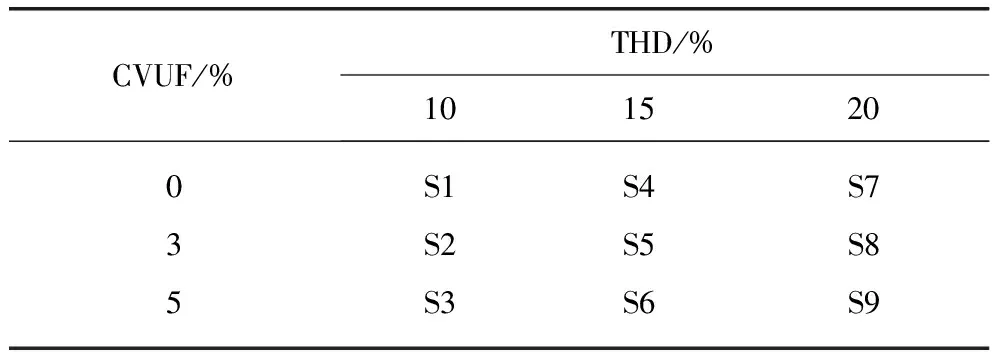
表1 各种谐波和不平衡共存的电压组合情况

1.2 计及谐波及磁路不对称的时步有限元模型

本文采用的时步有限元损耗计算模型的优势在于可以在计及磁路不对称、饱和及谐波等因素前提下，对电机内部任意单元的磁密与电密进行计算，在损耗计算方面具有明显优势。根据多截面法[10-11]，可得到时步有限元方程：

KX+DX′=F

(1)

式中： K、D——系数矩阵；X——状态变量；F——电源电压组成的激励项。

(1) 定子铜耗即为定子基波电流和谐波电流产生的损耗之和，表达式如式(2)所示：

(2)

图1 各种谐波和不平衡共存的电压波形

式中： PsCu——定子总铜耗； Rs——绕组电阻； ivA、ivB、ivC——各次谐波电流，其中v为谐波次数。

(2) 由于集肤效应的影响，转子导条电流分布是不均匀的。为了计及集肤效应的影响，必须对转子导条进行分区求解，表达式如式(3)所示：

(3)

式中： PrCu——转子总铜耗； σ——导条电导率； Lef——转子有效轴长； SΔ——区域各单元面积； JΔ——电流密度。

(3) 铁耗的求解采用经典三项式铁耗计算模型，其求解表达式如式(4)所示：

(4)

其中：

ke=π2γd2/(6ρ)

式中： PFe——铁耗密度； kh、x、ka——磁滞损耗系数及其指数项系数和异常损耗系数，通过对硅钢片实测损耗数据进行分离求解得出；

f——磁密的频率；

B——铁心磁密的幅值；

ke——涡流损耗系数。

γ——电导率；

d——硅钢片厚度；

ρ——铁磁材料密度。

对于谐波磁场的计及，可以通过对不同频率及磁密条件下的硅钢片实测损耗数据进行拟合求解，得出不同谐波条件下的损耗系数。

1.3 所用样机结构及主要参数

以一台Y132S-4—5.5kW感应电机为例，其基本参数及尺寸如表2所示。基于该参数，建立了时步有限元模型，如图2所示，其中左半部分为电机定转子基本结构，右半部分为有限元剖分网格图。

表2 电机参数及尺寸

图2 5.5kW感应电机有限元结构和剖分图

2 电源包含谐波及不平衡共存时电机内部磁场变化特点

定子铁心磁密主要谐波成分变化如图3和图4所示，可以看出：

(1) 定子齿部和轭部磁密的基波幅值是随电源不平衡度的增加而减小的，而电源电压谐波含量的大小对定子铁心基波磁密的影响较小。

(2) 电源电压谐波含量和电压不平衡度的大小对定子铁心谐波磁密的影响都非常大，尤其在电机满载的情况下。

转子铁心磁密主要谐波成分变化如图5和图6所示，可以看出：

图3 定子齿部(S1)的磁密随电源的变化特点

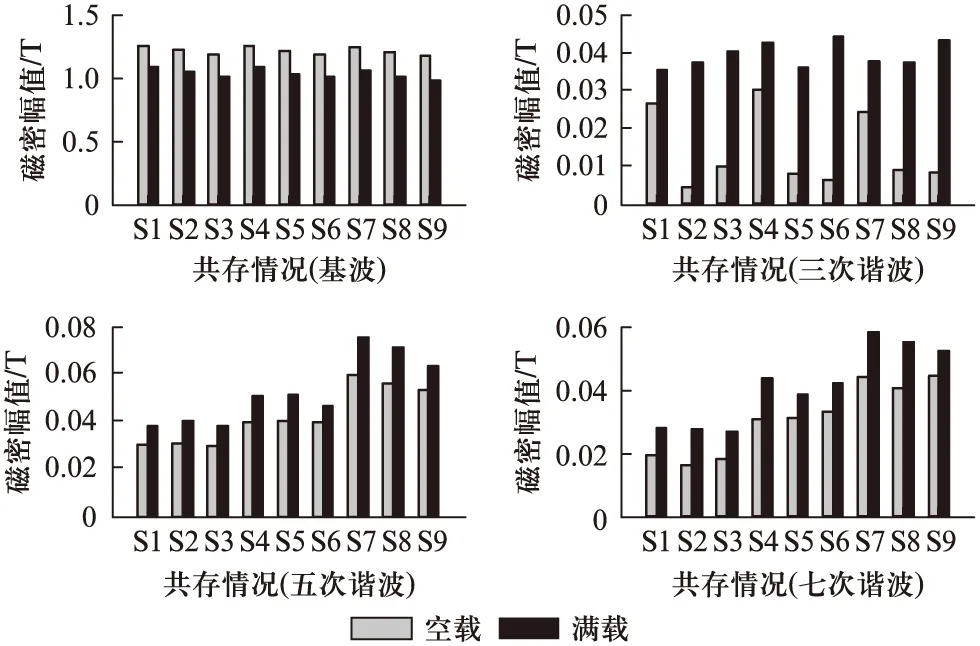
图4 定子轭部(S4)的磁密随电源的变化特点

图5 转子齿部(R1)的磁密随电源的变化特点

图6 转子轭部(R3)的磁密随电源的变化特点

(1) 电压不平衡度越大，转子侧铁心磁密2次分量的幅值将越大。当电压不平衡时将会在供电电压分解出负序分量，在转子导条中产生幅值非常大的2次谐波电流(如图7和图8所示)，进而产生负序旋转磁场。这些负序旋转磁场会在转子铁心磁密中产生大量的2次谐波成分。

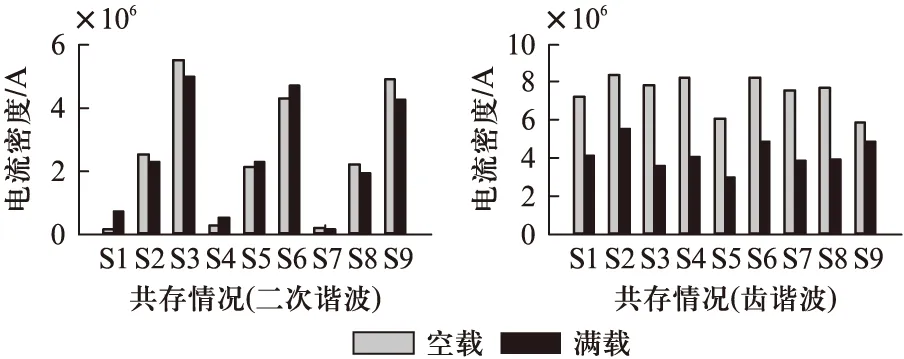
图7 转子导条RD1电密幅值随电源的变化特点

图8 转子导条RD2的电流幅值随电源的变化特点

(2) 电源电压谐波畸变程度和电压不平衡度的大小对转子齿谐波都有所影响。另外，由图5和图6还可以看出，空载条件下的齿谐波幅值要高于负载条件下的齿谐波幅值。

3 电源包含谐波及不平衡共存时电机内部损耗变化情况

各项损耗随电源电压不平衡度和谐波畸变率的变化情况如图9～图11所示。可知：

图9 电机定子铜耗随电源的变化特点

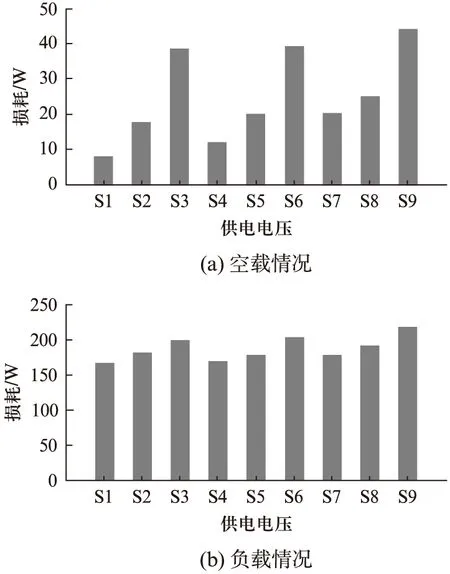
图10 电机转子铜耗随电源的变化特点

图11 电机铁耗随电源的变化特点

(1) 电机空载或轻载运行时，定转子铜耗主要随电压不平衡度的增加而明显增加；而定子铜耗随谐波畸变率的增加而增加不明显。例如，从图9(a)和图10(a)可以看出，电源谐波畸变率保持10%不变时，当不平衡度由0%增加到3%时，定子和转子铜耗分别增加9.2W和10.1W，增幅分别为16.2%和135%；而电源不平衡度为0%时，当谐波畸变率由10%增加到15%时，定子和转子铜耗分别仅增加0.9W和3.5W，增幅分别为1.6%和46%。

(2) 电机满载或重载运行时，定转子铜耗随电压畸变率和电压谐波含量的增加均有所增加，但增加幅度较小。例如，从图9(b)和图10(b)可以看出电源谐波畸变率保持10%不变时，当不平衡度由0%增加到3%时，定子和转子铜耗分别增加9.7W和16.4W，增幅分别为3.4%和9.2%；电源不平衡度为0%时，谐波畸变率由10%增加到15%时，定子和转子铜耗分别增加1.2W和5.6W，增幅分别为0.4%和3.2%。

(3) 电机铁耗满载和空载均随电源有所增加，但增加的幅度较小。例如，从图11可以看出当电源电压由S1变化到S2时，空载和满载铁耗分别增加2.3W和5.1W，增幅分别为2.0%和3.6%；电压由S1变化到S4时，空载和满载铁耗分别增加2.0W和4.7W，增幅分别为1.7%和3.4%。

4 试验验证

为了验证本文有限元仿真方法的正确性，针对前述5.5kW感应电机，采用Chroma 18600可编程电源产生前述供电电源波形给电机供电，并实测了其在空载和满载时的损耗，并将其与仿真结果对比，结果如图12所示。由图12可以看出实测与仿真基本一致，验证了有限元分析结果的正确性。

图12 电机损耗随电源变化的实测与仿真对比

5 结 语

本文利用时步有限元方法分析了当供电电压不平衡与谐波共存时，电机铁心内部的磁场与转子导条的电场的变化情况。结果表明，电源电压谐波畸变率与不平衡均对铁耗和铜耗有所影响；在电机空载运行时绕组铜耗随电压不平衡度的增加而明显增加，而随电压谐波畸变率的增加则不明显；无论是空载还是满载，电机铁耗随电压不平衡度和谐波畸变率均有所增加，但幅值均较小。

[1] SAXENA D， BHAUMIK S， SINGH S N. Identification of multiple harmonic sources in power system using optimally placed voltage measurement devices[J]. IEEE Transactions on Industrial Electronics， 2014，61(5)： 2483-2492.

[2] DLALA E， ARKKIO A. A general model for investigating the effects of the frequency converter on the magnetic iron losses of a squirrel-cage induction motor[J]. IEEE Transactions on Magnetics， 2009，45(9)： 3303-3315.

[3] KIM J W， KIM B T， KWON B I. Optimal stator slot design of inverter-fed induction motor in consideration of harmonic losses[J]. IEEE Transactions on Magnetics， 2005，41(5)： 2012-2015.

[4] WANG Y J. Analysis of effect of three-phase voltage unbalance on induction motors with emphasis on the angle of the complex voltage unbalance factor[J]. IEEE Transactions on Energy Conversion， 2001，16(3)： 270-275.

[5] DYMOND J H， STRANGES N. Operation on unbalanced voltage： one motor’s experience and more[J]. IEEE Transactions on Industry Applications， 2007，43(3)： 829-837.

[6] ANWARI M， HIENDRO A. New unbalance factor for estimating performance of a three-phase induction motor with under and overvoltage unbalance[J]. IEEE Transactions on Energy Conversion， 2010，25(3)： 619-625.

[7] 黄平林，胡虔生.PWM逆变器供电下电机铁心损耗的解析计算[J].中国电机工程学报，2007，27(12)： 19-23.

[8] ZHANG Y， LI Y W. Investigation and suppression of harmonics interaction in high-power PWM current-source motor drives[J]. IEEE Transactions on Power Electronics， 2015，30(2)： 668-679.

[9] GMYREK Z， BOGLIETTI A， CAVAGNINO A. Estimation of iron losses in induction motors： calculation method， results， and analysis[J]. IEEE Transactions on Industrial Electronics， 2010，57(1)： 161-171.

[10] 江建中，傅为农.斜槽异步电动机的多截面有限元法分析[J].电工技术学报，1997，12(5)： 11-15.

[11] 赵海森，刘晓芳，罗应立，等.转子斜槽及不同槽斜度对鼠笼式异步电机损耗影响的时步有限元分析[J].中国科学： 技术科学，2011(10)： 1380-1387.

Loss Characteristics of Induction Motor under Power Source with Harmonic Components and Unbalance Voltage Conditions*

ZHANGDongdong1，ZHAOHaisen1，ZHAOWeibo1，WANGShasha1，BAIZhijun2

(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources， North China Electric Power University， Beijing 102206， China； 2. Gansu Liujiaxia Hydropower Station， Yongjing 731600， China)

Due to enormous applications of the non-linear and unbalance load， simultaneous voltage unbalance and harmonic distortions are often encountered in power supply， and the operating performance of the induction motors may be worse， such as loss increases and temperature rise. In order to study the loss characteristics of induction motor whose power supply has both harmonic components and unbalance voltage， the characteristics of field distribution and loss characteristics of a 5.5kW cage induction motor by using the Time-stepping Finite Element method were analyzed. The loss characteristics of no-load and load were analyzed, and the correctness of the analysis results was verified by experiments.

harmonic； unbalance voltage conditions； time-stepping finite element； loss

国家自然科学基金项目(51307050)；中央高校基本科研业务费专项资金资助(2015ZD03)

张冬冬(1990—)，男，硕士研究生，研究方向为交流电机能耗分析。 赵海森(1982—)，男，博士，副教授，研究方向为电机内电磁场数值计算、电机系统节能及新型节能电机设计。

TM 346

A

1673-6540(2016)07-0045-06

2016-01-12