直接转矩控制中定子磁链观测方案对比研究

杨 影， 黄 锐， 余衍谱

(上海大学 机电工程与自动化学院，上海 200072)

直接转矩控制中定子磁链观测方案对比研究

杨 影， 黄 锐， 余衍谱

(上海大学 机电工程与自动化学院，上海 200072)

定子磁链的有效观测直接决定转矩控制的稳定性。针对纯积分观测定子磁链存在的问题，对一阶惯性环节、幅值限定的改进积分器、一阶惯性环节串联HPF三种定子磁链观测方案进行了深入比较分析。定量分析了一阶惯性环节中截止频率对相位和幅值偏差的影响，给出了截止频率的选择依据；结合原理结构图分析了幅值限定改进积分器的效果；对比幅频特性图并得到带补偿的一阶惯性环节串联HPF环节。对幅值限定的改进积分器较一阶惯性环节带来幅值和相位的误差进行了补偿；而一阶惯性环节串联HPF则可以完全消除直流偏置和积分初值问题，进一步提高定子磁链的估算精度。通过仿真和试验进行了对比验证。

直接转矩控制； 定子磁链观测； 积分器； 一阶惯性环节串联HPF

0 引 言

直接转矩控制(Direct Torque Control, DTC)是一种高动态性能的交流调速方法，具有结构简单、动态响应快、鲁棒性好等优点[1-2]。其核心是在保持定子磁链幅值|ψs|恒定的条件下通过控制转矩角δ直接控制电磁转矩Te。因而定子磁链的有效观测直接决定转矩控制的稳定性。定子磁链幅值观测不准，将导致定子电流波形畸变，输出转矩过大或过小，严重时将导致电机不能正常运行；定子磁链相位观测不准，会导致输出转矩的过大或过小，影响系统运行性能。若相位观测误差大于30°电角度，则会在错误的扇区里选择错误的电压矢量，导致控制失败[3]。因此，准确地获取定子磁链的真实信息至关重要[4]。

传统的定子磁链观测方法有电流模型法[5]和电压模型法[6]。电流模型法利用电流、电感和转子电角度计算定子磁链，对转子角度检测精度要求较高，依赖电机参数，因此在不同工况下运行会导致磁链估算误差。电压模型法利用反电动势积分估计定子磁链，因仅依赖于电机定子电阻参数，故具有鲁棒性强、易于实现等优点[7]。因而在DTC中一般采用电压模型估算定子磁链。但在实际应用中采用纯积分器存在着直流偏移累积误差和积分初值问题。因而国内外学者提出了很多改进定子磁链计算的方案。目前广泛采用一阶惯性环节代替纯积分环节，可以有效地抑制直流偏移累积误差，但在低速时又存在着严重的幅值和相位误差[8]。为此文献[9]提出了带有饱和反馈的积分算法、带有幅值限幅的积分算法和带有自适应补偿的积分算法来估计定子磁链。饱和反馈的改进积分器通过对输出限幅使改进积分器在纯积分和一阶惯性环节两种形式之间来回切换而得以实现。它会使输出磁链波形畸变并带来附加的谐波，且限幅值需要正好和输出波形的幅值相等才能效果最佳，在切换过程中，相位也将突变。幅值限定的改进积分器是通过极坐标和笛卡尔坐标间的坐标变换将相位与幅值的反馈通道分离，可消除相位的突变，减小谐波分量。自适应补偿的改进积分器是通过检测电机的定子磁链与定子感应电动势的正交性来自动调节磁链补偿程度，适用于磁链幅值不恒定的场合，如： 最大转矩电流比控制，定子磁链幅值需要随电磁转矩同步给定以实现最大电流比控制，且引入了PI调节器，增加了参数调试难度。一阶惯性环节串联HPF方案则可以消除直流分量累积误差。

因此本文针对初始定位偏差、直流分量累积误差、幅值和相位偏差等问题对基于一阶惯性环节、幅值限定的改进积分器、一阶惯性环节串联HPF三种定子磁链观测方案进行对比研究，包括频域特性对比分析和仿真、试验验证。

1 定子磁链观测方案对比分析

1.1 基于一阶惯性环节的定子磁链观测

电压模型利用定子反电动势Es积分得到定子磁链ψs，其关系为

(1)

由式(1)可看出纯积分器存在直流偏移累积误差和积分初值问题，因此实现时多采用一阶惯性环节1/(s+ωc)代替纯积分器。一阶惯性环节也可称为一阶惯性滤波器(Low Pass Filter， LPF)。其信号传递如图1所示。

图1 一阶惯性环节的信号传递图

图1中1/s代表纯积分器，s/(ωc+s)代表高通滤波器(High Pass Filter， HPF)。组合得到一阶惯性环节，其中纯积分器正是计算定子磁链所需算法，其输出的定子磁链中含有的初值偏差和直流分量累积误差可以通过HPF滤除或衰减。

为了定量说明，假定输入为带有微小直流分量B的交流信号：x(t)=Aωsinωt+B。经LPF环节后输出信号y(t)如式(2)所示：

(2)

式中：Δθ——相移，Δθ=-arctan(ωc/ω)；C——和初始条件相关的系数。

可以看出LPF能使初始条件造成的直流分量Ce-ωct随着时间增长衰减至0，输出直流分量B/ωc不会随着时间累积，提高截止频率ωc可以更有效抑制直流分量。

但LPF估计定子磁链存在相位偏差Δθ和幅值偏差ΔG，如式(3)～式(4)所示：

Δθ=-arctan(ωc/ω)

(3)

(4)

为了确定截止频率的取值范围，定义k=ωc/ω为变量，分析不同截止频率下LPF带来的幅值偏差和相位偏差，如图2所示。由于DTC中估算的定子磁链相位偏差超过30°易造成扇区误判而导致电压矢量选择错误，严重时会导致系统运行失败，因此k值不能太大，太小则对直流分量抑制不够充分，故k值常设定为0.1～0.5[10]，此时定子磁链相位偏差在-5.7°～-26.6°，幅值偏差在1.00～1.12倍。因此需要根据实际电机转速n来同步修改截止频率ωc。

图2 不同截止频率下LPF带来的幅值偏差和相位偏差

1.2 基于幅值限定的改进积分器的定子磁链观测

LPF能抑制定子磁链ψs中的直流分量，但会带来较大的相位滞后和幅值偏差。因此可以进行幅值和相位补偿来改善低速性能。

具有幅值限定的改进积分器结构如图3所示。输入为反电动势，输出为定子磁链。

图3 幅值限定的改进积分器结构图

该磁链观测器输出为

(5)

式中：Z——补偿信号。

当电机高速运行时，反馈模块的增益接近为0，方案为LPF。反馈对输出的影响很小，能够很好地观测磁链。在低速下，反馈分量对抑制直流偏移饱和起着重要作用。若输出信号ψs不超过限幅基准L，那么积分器的补偿信号Z等于积分器的输出信号ψs，若超过限幅基准L，反馈磁链幅值限定为L，此时方案为纯积分器。

由于饱和限幅器只对磁链幅值进行限幅，而对相位没有影响，磁链幅值被限制，不会随时间增大而增大。若饱和限定基准设为定子磁链额定幅值，则满足DTC定子磁链幅值恒定的要求，相角误差小，很适合磁链幅值恒定的DTC方案。

1.3 基于一阶惯性环节串联HPF的定子磁链观测

具有幅值限制的改进型积分器实质上是一个改良的低通滤波器，可以抑制直流偏置，但不能从根本上消除直流偏置。HPF具有抑制低频分量、消除直流分量的能力，因此HPF串联一阶惯性环节的定子磁链估算方案，如图4所示，不仅解决了初值误差问题，而且实现了磁链零直流偏置。

图4 一阶惯性环节串联HPF的信号传递图

图5为纯积分、一阶惯性环节和一阶惯性环节串联HPF的波特图，一阶惯性环节的截止频率ωLc为20rad/s，HPF的截止频率ωHc为10rad/s。

图5 纯积分、一阶惯性环节和一阶惯性环节串联HPF的波特图

反电动势Es经过一阶惯性环节和HPF后，与定子磁链的关系为

(6)

比较式(1)和式(6)，可得定子磁链的补偿关系为

(7)

将式(7)中磁链在α、β坐标下分成实部、虚部展开，得到带补偿的串联HPF的一阶惯性环节定子磁链估算实现方案，如图6所示。

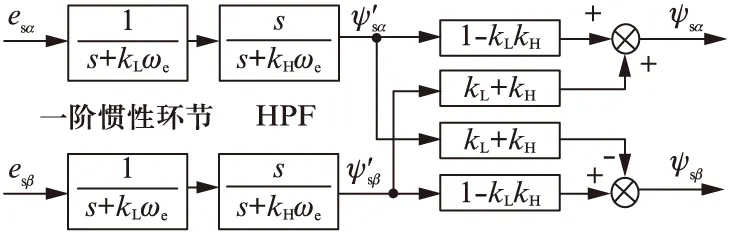
图6 电压模型定子磁链估算方案原理图

2 仿真与试验分析

为了对以上三种定子磁链观测方案进行对比研究，在MATLAB/Simulink环境下构建了离散化的占空比调制DTC系统仿真平台。所用PMSM电机参数如表1所示。

表1 电机参数

仿真验证中，通过在反电动势信号上加入1%的直流分量模拟实际系统中的直流分量。图7为电机在空载情况下，转速给定为300r/min，在不同定子磁链估算方案下α轴的磁链分量仿真响应曲线。截止频率ωc随实际转速n同步修改(k=0.5)，限幅值L均为0.0835。图7中1为占空比DTC系统的真实定子磁链α轴分量波形，2、3、4依次为LPF、幅值限定改进积分器和补偿一阶惯性环节串联HPF估算的定子磁链α轴分量波形。

由图7可以看出LPF估算定子磁链方案会带来相位和幅值的偏差，幅值限定的改进积分器能够对幅值和相位进行补偿，与真实值有较小的相位偏差。带补偿的串联HPF的一阶惯性环节的方案则能够很快地无误差跟随真实值，可以完全消除直流偏置的影响。

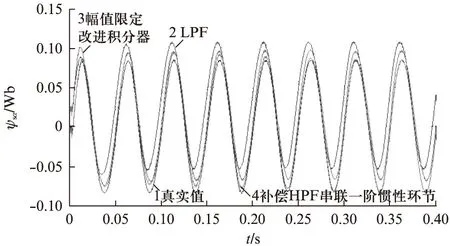
图7 不同定子磁链估算方案下α轴的磁链分量仿真响应曲线

为验证方案的可行性，搭建了基于浮点型DSP芯片TMS302F28335的PTC硬件平台，采用电机自带的2500P/R增量式光电编码器测速，主中断周期为5e-5s，磁链滞环宽度为0，转矩滞环宽度设置为0.2，系统中硬件电路母线电流保护值6.67A，软件电流限幅值为6A。图8为永磁同步电机占空比调制DTC系统在空载情况下，定子磁链估算方案采用具有幅值限定的改进积分器方案，并同步观察随电机转速同步修改截止频率ωc(k=0.5)的LPF方案，在200r/min转速下定子磁链在α轴上分量波形。

图8 PMSM占空比DTC系统在两种估算方案的α轴磁链试验波形

由图8对比LPF和幅值限定的改进积分器两种方案可得，LPF会带来幅值和相位的偏差，幅值限定的改进积分器则可有效地进行补偿，并改善PMSM占空比DTC系统在低速区的定子磁链估算，进而拓宽DTC系统的调速范围。图9为占空比DTC系统在1000r/min时，对于HPF串联一阶惯性环节磁链观测方案，一阶惯性环节带来的偏差在补偿前后的定子磁链α分量试验波形。由图9可以看出补偿前定子磁链相位超前，幅值偏小。图10(a)为占空比DTC 300r/min转速下转矩和磁链试验波形，图10(b)为定子磁链圆。磁链分量幅值平稳，系统稳定性能良好。

图9 HPF串联一阶惯性环节方案定子磁链分量补偿前后试验波形

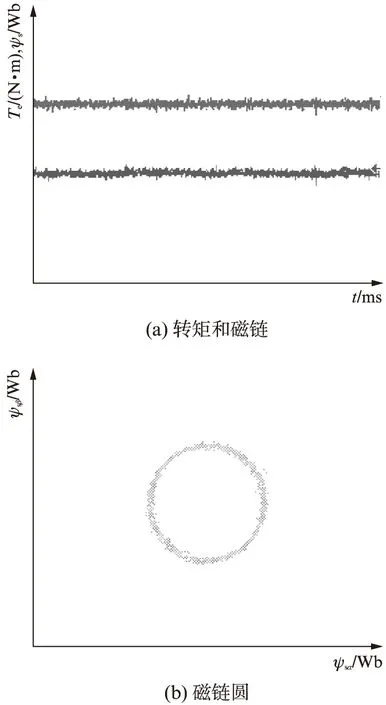
图10 300r/min时的转矩和磁链试验波形

3 结 语

本文对基于反电动势的定子磁链估算的实现方案进行了深入比较分析，主要针对初始定位偏差、直流分量累计误差、幅值和相位偏差等问题对LPF、幅值限定的改进积分器、HPF串联一阶惯性环节方案进行了理论分析。LPF可以有效地抑制直流分量累积误差和积分初始值问题，但存在一定的幅值和相位偏差，幅值限定的改进积分器可对幅值和相位进行补偿；HPF串联一阶惯性环节方案则可以完全消除直流偏置和积分初值问题，提高了定子磁链的估算精度，使系统具有良好的动、静态性能。仿真与试验结果验证了理论分析的正确性。

[1] 赵争鸣，袁立强，孟朔，等.通用变频器矢量控制与直接转矩控制特性比较[J].电工技术学报，2004，19(4)： 81-84.

[2] 冯涛，陆华.永磁同步电机直接转矩控制及仿真[J].电机与控制应用，2013，40(6)： 27-31.

[3] 曹文超.永磁同步电机直接转矩控制的定子磁链观测方法研究[D].武汉： 华中科技大学，2011.

[4] 邓勇.高性能永磁同步电机直接转矩控制策略研究[D].重庆： 重庆大学，2008.

[5] 金孟加，邱建琪，史涔溦，等.基于新型定子磁链观测器的直接转矩控制[J].中国电机工程学报，2005，25(24)： 139-143.

[6] ZHONG L， RAHMAN M F， HU Y W， et al. Analysis of direct torque control in permanent magnet synchronous motor drives [J]. IEEE Transaction on Power Electronics， 1997，12(3)： 528-535.

[7] ZHAO K Q， WU H X， YU Z W. A DTC-SVM method with flux observer based on rotor position and current model for SPMSM control system[C]∥Industry Applications Society Annual Meeting(IAS)， Las Vegas， 2012： 1-6.

[8] BOSE B K， PATEL N R. A programmable cascaded low-pass filter-based flux synthesis for a stator flux-oriented vector-controlled induction motor drive[J]. IEEE Transactions on Industrial Electronics， 1997，4(1)： 140-143.

[9] HU J， WU B. New integration algorithms for estimating motor flux over a wide speed range[J]. IEEE Trans On Power Electronics， 1998，13(5)： 969-977.

[10] HINKKANEN M， LUOMI J. Modified integrator for voltage model flux estimation of induction motor[J]. IEEE Trans Ind Electron， 2003，50(4)： 818-820.

[11] 孙大南，林文立，刁利军，等.改进型感应电机电压模型磁链观测器设计[J].北京交通大学学报，2011，35(2)： 94-98.

Comparative Research of Stator Flux Observer in Direct Torque Control

YANGYing，HUANGRui，YUYanpu

(College of Mechanics Engineering and Automation， Shanghai University， Shanghai 200072， China)

The stability of the torque control was directly decided by the effective of the stator flux observation， for the problem of stator flux in the pure integral observation， the first order filter， the amplitude limited of improved integrator， the first order filter series HPF three schemes of the stator flux observer were in-depth analyzed in comparison. Quantitative analysis of the influence of the first-order filter in the cutoff frequency of the phase error and amplitude deviation， and the selection basis of the cutoff frequency was given； The effect of the amplitude limited of improved integrator was analysed with the principle construction diagram； Comparing amplitude-frequency characteristic diagram and obtaining the first order filter series HPF with compensation. The amplitude limited of improved integrator could make a compensation for amplitude and phase deviation compared to the first order filter； and the first order filter series HPF could completely eliminate the dc bias and integral initial value problems， made a big improvement to the estimation precision of the stator flux. The comparison verification was carried out with the simulation and experiment.

direct torque control(DTC)； stator flux observer； integrator； first order filter series HPF

杨 影(1979—)，女，工学博士，副教授，研究方向为高性能伺服控制系统。

TM 343

A

1673-6540(2016)07-0007-05

2015-12-31