永磁同步电机温度场分析与水道结构优化*

王淑旺， 高月仙， 谭立真

(合肥工业大学 汽车与机械工程学院，安徽 合肥 230009)

永磁同步电机温度场分析与水道结构优化*

王淑旺， 高月仙， 谭立真

(合肥工业大学 汽车与机械工程学院，安徽 合肥 230009)

以一台额定功率为30kW的车用永磁同步电机为例，建立三维瞬态热分析模型，分析散热边界条件。针对定转子间气隙处理问题，提出一种改进的泰勒数判别与计算等效导热系数的方法，合理处理定转子间复杂的对流换热情况，并进行试验验证。根据传热学和流体力学的理论知识，建立对流换热系数以及压降与水道结构参数间的关系，给出一种水道截面尺寸的选择方法，结合MATLAB和CFD数值计算软件找出合适的水道结构截面尺寸范围并进行仿真，对实际工程中电机的水道结构设计具有一定的指导意义。

永磁同步电机； 边界条件； 温度场； 对流换热系数； 截面尺寸； 水道结构

0 引 言

电动汽车有限的安装空间使得电机须具备较高的功率密度和效率，加之复杂的路况和驾驶习惯等使电机运行工况十分复杂，温升严重。电机温升或局部温升过高，不仅会导致结构变形，还会使电机耐压和绝缘性降低，严重影响使用寿命[1]。反之，则造成生产过程中材料的浪费，增加制造成本。因此对电机各部分温升的准确计算以及冷却系统的合理设计对电机安全运行具有十分重要的意义[2]。

对温升的计算，国内外主要采用简化公式法、等效热路法、数值计算法[3]。等效热路法精度较简化公式法高，但依赖于所建模型节点数[4]；数值计算法计算精度高，现已得到广泛应用。目前要准确分析电机温度场还存在一定困难，首先，热源的准确确定有一定难度；其次，绕组的简化方法尚不成熟；再者，转子旋转问题尚未能较好地解决[5]。电机电磁结构确定后，温升的主要影响因素是冷却系统的设计，合理的冷却结构对提高电机的散热效果意义重大。

本文采用数值计算法，综合国内外关于电机热边界条件的设定，对车用水冷永磁同步电机进行全域温度场仿真并进行相应的试验验证；同时建立冷却水道结构参数和对流换热系数以及压降之间的关系式，分析水道结构参数对对流散热系数和流体压降的影响，据此选出水道结构参数的较好范围，再利用CFD软件对优选结构仿真，最终确定最佳水道结构。

1 三维温度场全域瞬态数值计算模型

1.1 求解域模型

本文以水冷永磁同步电机为例。电机参数如表1所示。

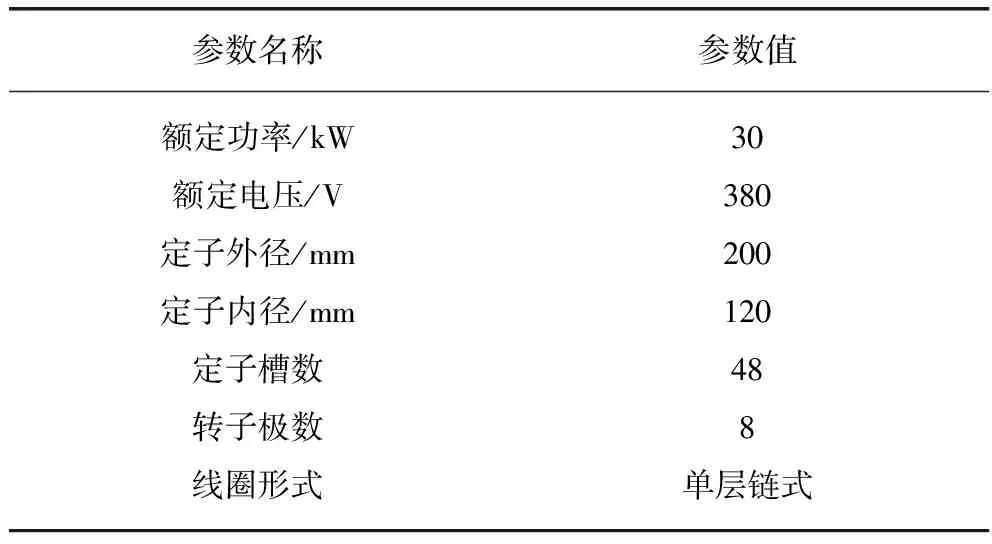
表1 电机的基本参数

为节省计算时间，同时又满足工程实际需要，对仿真模型进行如下假设：

(1) 电机运行产生的热量全部由冷却水带走；

(2) 忽略摩擦和风阻两种基本的机械损耗；

(3) 工作产生的各项损耗均匀分布在热源内。

求解域模型如图1所示。

图1 永磁同步电机三维全域模型

1.2 热性能参数计算

1.2.1 气隙的等效处理

计算电机三维全域温度场时，需考虑定转子之间的气隙散热。气隙内空气在转子的拖拽下做周向流动，两个相对旋转的同心圆柱环形缝隙间的流体运动是典型的泰勒-库特流。

雷诺数计算时假设定转子表面为光滑圆柱面，而实际气隙换热受表面粗糙度和开槽影响。本文用泰勒数代替雷诺数判断气隙的运动状态，同时根据文献[6]考虑定转子开槽的影响，永磁同步电机仅存在定子开槽时，散热量有10%的提升。

气隙间泰勒数可表示为[7-9]

(1)

其中：

δ=r2-r1

式中： ω——转子转速，rad/s； δ——气隙尺寸，m； r1——转子外半径，m； r2——定子内半径，m； ν——流体的运动粘度，m2·s。

临界泰勒数Tacr=41.19。

当Ta<41.19时，定转子间气隙流为层流，努塞尔数Nu=2，此时散热主要靠热传导。

当41.19

Nu=0.212Ta0.63Pr0.27

(2)

当Ta>100时，此时流动发展为完全紊流：

Nu=0.386Ta0.5Pr0.27

(3)

则可求出气隙内对流换热系数：

(4)

式中：Pr——流体的普朗特数；λa——空气的导热系数，W/(m·K)；k——考虑表面粗糙度和定子槽开口时的系数，取值为1.32。

实际建模时将旋转的转子视为静止，假设定转子间空气静止，静止空气所传递的热量应与流动空气所传递的热量相同，使用等效导热系数来代替对流换热系数。

1.2.2 绕组等效绝缘层

电机绕组采用散下线结构，仿真前须对其进行合理的简化和等效。根据文献[2]来计算等效导热系数。

1.2.3 定子壳体接触热阻

定子与壳体内表面由于装配工艺、材料及实际安装加工等原因，存在装配间隙，所以应使用文献[10]的经验公式计算。为避免计算量增加，用等效接触热阻代替等效装配间隙。

1.2.4 热源分布

电机损耗是温升的来源，永磁同步电机损耗包括绕组铜耗、定子铁耗、转子铁耗和永磁体损耗。因采用强制水冷没有通风系统，故可忽略机械损耗和附加损耗。额定工况下损耗值分布如表2所示。

表2 额定工况下损耗值分布 W

2 电机温度场计算结果分析比较

仿真得到电机的温度场如图2所示。

图2 电机温度分布

从图2可以看出，电机整体的最高温度出现在绝缘和绕组上，为97.131℃。电机绕组两端温度较高，且最高温度出现在绕组较长一侧，而在水道覆盖的中间范围内，由于冷却液的作用，散热条件良好，温度较低。

为验证仿真的准确性，对电机在额定负载情况下的温升情况进行了试验。试验台架包括电机、控制器、测功机、水管等，如图3所示。试验过程中记录的电机绕组温升情况和仿真温升对比，如图4所示。

图3 试验台架

图4 试验和仿真温升情况

试验测得最高温升为93.5℃，与仿真所得绕组最高温度97.131℃相近，误差较小，且仿真温度变化与试验相近，比较合理，从而验证了仿真的正确性与准确性。

3 水道结构尺寸选择

实际水道设计过程中不仅要考虑散热效果，还要兼顾水泵的工作负荷，是一个综合传热学和流体力学的多领域问题[11]。本文通过对周向折流式平行水道的对流换热系数和流体阻力进行分析，对比不同水道结构参数下电机的散热性能，并优化改进。假设流量不变，为10L/min。初始水道结构尺寸如表3所示。

表3 初始壳体水道结构基本尺寸

3.1 水道评价标准

3.1.1 对流换热

电机工作过程中生成的热量主要由冷却水和壳体间的对流换热带走。对流换热带走的热量可由牛顿冷却公式计算：

Φ=AfhfΔT

(5)

由式(5)可知，要提高对流换热量，必须提高对流换热面积Af、对流换热系数hf和流体和固体间温差ΔT。对温差ΔT的控制一般通过降低冷却液温度，不涉及水道结构，故不作考虑。

该电机中水道对流换热面面积计算为

Af= 2πr·2an+2πr·2hn=

4πrn(a+h)

(6)

对流换热是一个复杂的热量交换过程，其换热系数受流体介质、流体状态、是否有相变以及换热表面几何形状等很多因素的影响。单相强制对流换热系数可按式(7)[12]表示：

h=(λ，l，v，υ，λ，cp)

(7)

式中：l——特征尺寸；v——流速；cp——流体的恒压热容。

3.1.2 管流压降

管流压降在工程计算中十分重要且常用，设计水道时要综合考虑压降的影响。它的计算公式为[13]

(8)

由于电机采用的是折返式水道，相邻水道连通处存在折弯，水流经过时方向会发生变化，导致局部压降：

(9)

式中：ks——局部阻力系数。

冷却液管道的总压降为管流压降和局部压降之和，即

Δp=Δp1+Δp2

(10)

3.2 参数范围选择

对流换热需同时取得最大对流换热面积和对流换热系数方可获得最佳散热效果，故根据牛顿冷却公式，采用换热系数和换热面积的乘积为选择依据。

根据式(5)～式(7)，利用MATLAB绘制出对流换热面积与换热系数乘积随a、h变化关系，如图5所示。

图5 对流换热系数与换热面积乘积随截面参数变化关系

由图5可看出，流量一定时，由于h的范围有限，a的影响要比h更显著，因此将h选为5mm，在后面的分析中作为常量。

仅考虑水道截面宽度a时，根据式(7)、式(10)分别绘出截面宽度a与对流换热系数及流阻的变化关系图，如图6、图7所示。根据图形的变化趋势及实际情况，选出合适的参数范围。

图6 对流换热系数随截面长度a的变化关系

从图6可知，截面宽度a越小，对流换热系数越大，则散热能力也在增强；且随a的减小，其变化率越大，25mm以上变化趋势比较平缓。压降与a的关系与对流换热系数与a的关系相似，从图7可知，15mm以下时，压降变化十分显著；所以取较小的a值虽然可以获得较大的对流换热系数，增大换热量，但由于相应水流速度的增大，使得进水口所需要压力随之增大，且会使得流阻增加，管流总压降变大，流体流经管道的沿程损失也越大。因此结合图6～图7的曲线变化趋势，确定a的取值范围为15～25mm，计算出相应的水道数目在5～8之间，其对应关系如表4所示。

图7 管流压降随截面长度a的变化关系

表4 不同水道数和截面宽度下参数分布表

4 数值计算进一步优选结果

为进一步确定几种水道的散热效果，继续用CFD仿真软件分别进行热仿真并验证，选出散热效果最佳的模型。

电机最高温度出现在绕组端部，优化水道结构时可忽略转子影响，将绕组、绝缘等复杂结构等效为一个均匀的发热体，着重分析水道结构尺寸对散热的影响。水道的简化模型如图8所示。

图8 简化后的电机求解域模型

冷却水流量保持10L/min不变，根据模型求解得到不同水道下温度和压力分布，如表5、表6所示。

表5 水道数和最高温度的关系

表6 水道数和压力的关系

由表5可知，初始水道结构绕组的最高温度达104.1℃，优化后绕组温度均有所降低，水道数为5时，最高温度为102.0℃，比原来降低2.1℃；6、7、8水道数分别降低2.3℃、2.5℃和2.3℃。

由表6可知，当水道数增加时，流体的压降也在迅速增加，水道数为8的压降要远大于5、6、7水道数，与理论分析结果一致。

综上分析，本电机水道截面宽度在17～25mm，即水道数目在5～7比较合理，可以达到较好的散热效果，同时水道流阻又控制在较小范围内。

5 结 语

本文对一台永磁同步电机热边界条件进行分析，并进行额定转速下瞬态温度场的数值模拟计算。在定转子间气隙的处理上，通过泰勒数考虑定子表面粗糙度和开槽的影响，保证仿真的精度，并为电机温度场计算和理论分析提供了依据，同时辅以试验对仿真结果进行验证，证明了仿真的准确性。

通过构建对流换热系数、流体压降与水道截面参数间的关系，对其进行定量分析，运用数学软件绘制出关系图，根据参数间关系的变化趋势，对水道结构进行优选，确定出合理的截面参数范围，同时确定水道数目；利用数值计算软件得出相应结构下的温度分布，结果与理论计算相符，故水道数目取在5～7比较合适，即水道截面宽度在17～25mm，验证了理论的正确性。这对电机的水道结构设计具有一定的指导意义。

[1] 胡萌，李海奇，李旭光，等.电动车用水套冷却永磁电机损耗及温度[J].电机与控制应用，2014，41(1)： 27-32.

[2] XYPERAS J， HATZIATHANASSIOU V. Thermal analysis of an electrical machine taking into account the iron losses and the deep-bar effect[J]. IEEE Transactions on Energy Conversion， 1999，14(4)： 996-1003.

[3] 李和明，李俊卿.电机中温度计算方法及其应用综述[J].华北电力大学学报，2005，32(1)： 1-5.

[4] 何磊，王心坚，宋国辉.基于热阻网络法的电机瞬态温度场分析[J].佳木斯大学学报(自然科学版)，2014，32(2)： 187-190.

[5] 李伟力，李守法，谢颖，等.感应电动机定转子全域温度场数值计算及相关因素敏感性分析[J].中国电机工程学报，2007，27(24)： 85-91.

[6] HAYASE T， HUMPHERY J A C， GREIF R. Numerical calculation of convective heat transfer between rotating coaxial cylinders with periodically embedded cavities[J]. Trans SME Heat Transf， 1992，114(3)： 589-597.

[7] 李青青，黄勤，杨立，等.永磁同步电机水冷系统散热参数分析与热仿真[J].机械设计与制造，2014(4)： 188-191.

[8] HOWEY D A， CHILDS P R N， HOLMES A S. Air-gap convection in rotating electrical machines[J]. IEEE Transactions on Industrial Electronics， 2012，59(3)： 1367-1375.

[9] STATON D， BOGLIETTI A， CAVAGNINO A. Solving the more difficult aspects of electric motor thermal analysis in small and medium size industrial induction motors[J]. IEEE Transactions on Energy Conversion， 2005，20(3)： 620-628.

[10] 黄国治，傅丰礼.中小旋转电机设计手册[M].北京： 中国电力出版社，2014.

[11] 梁培鑫，柴凤，李翠萍，等.水冷电机水路设计的研究[J].微电机，2013，46(5)： 1-4.

[12] 赵镇南.传热学[M].北京： 高等教育出版社，2002.

[13] 陈卓如，王洪杰，刘全忠，等.工程流体力学[M].北京： 高等教育出版社，2013.

[14] 李翠萍，柴凤，程树康.冷却水流速对汽车水冷电机温升影响研究[J].电机与控制学报，2012，16(9)： 1-8.

[15] 李翠萍.微型电动汽车用感应电机的冷却系统研究[D].哈尔滨： 哈尔滨工业大学，2013.

Analysis of Temperature Field of Permanent Magnet Synchronous Motor and Water Jacket Structure Optimization*

WANGShuwang，GAOYuexian，TANLizhen

(College of Mechanical and Automotive Engineering， Hefei University of Technology， Hefei 230009， China)

The transient temperature field of a 30kW permanent magnet synchronous motor was established， and then the thermal boundary conditions were analyzed. Dealing with the complex convective heat transfer within the air gap between the stator and the rotor， an improved method was proposed to calculate equivalent heat conductivity coefficient and the result accuracy of simulation was testified. According to the theory of heat transfer and hydromechanics， the mathematical relationships between structure parameters of water jacket and convective heat-transfer coefficient， pressure drop were set up so a selection method was provided for sectional dimension of water jacket： combining MATLAB and CFD to find the suitable dimension range for water jacket and simulate. It would be of great help， when this method was applied in actual engineering motor water jacket design.

permanent magnet synchronous motor(PMSM)； boundary condition； temperature field； convective heat-transfer coefficient； sectional dimension； water jacket structure

混合动力乘用车机电耦合系统开发及产业化(1501021004)

王淑旺(1978—)，男，博士，副教授，研究方向为电动汽车电驱动系统和汽车自动化装备。

TM 351

A

1673-6540(2016)07-0051-06

2015-12-14