基于ANSYS/LS-DYNA的切削过程有限元模拟

杨洪波，胡三恩，李秀全，李明娜（甘肃蓝科石化高新装备股份有限公司，甘肃兰州730000）



基于ANSYS/LS-DYNA的切削过程有限元模拟

杨洪波，胡三恩，李秀全，李明娜
（甘肃蓝科石化高新装备股份有限公司，甘肃兰州730000）

摘要：金属切削过程是一个非常复杂的弹塑性变形过程。本文运用有限元分析理论及弹性力学理论，充分考虑到材料的本构关系、切屑与材料的分离准则以及切屑与刀具间的接触与摩擦，运用数值仿真软件LS-DYNA（一款非线性显式动力学分析软件）对切削过程进行有限元分析。结果表明：切屑的形成过程是材料受到刀具挤压产生剪切滑移的过程；最大等效应力在切削起初迅速增大直至一定值附近波动，此时进入切削稳定状态；最大等效应力随着切削速度的增大而减小；切削厚度越大，最大等效应力越大。

关键词：金属切削；本构关系；数值仿真；最大等效应力；剪切滑移

金属切削加工是切除毛坯件上多余材料的一种机械加工技术，随着计算机仿真技术的发展，学者们提出了各种切削模型，并利用仿真软件切削过程进行有限元分析，得到了切削过程中的应力、应变、温度分布以及刀具钝角半径对切削过程的影响[1]，为研究切削机理提供了重要手段。随着商业化有限元分析软件的陆续上市，免掉了试验人员编程浪费的宝贵时间[2]，分析更加方便快捷，且具有通用性。

本文利用非线性显式动力学分析软件LS-DYNA仿真不同切削条件下的切削过程，分析切屑速度、切削厚度与最大等效应力之间的关系。

1　有限元模型

1.1几何模型建立

对于本文中的模型建立使用2维实体单元PLANE162，在ANSYS/LS-DYNA中有Lagrange、Euler和ALE3种算法，其中Lagrange法可使物体结构形状和单元网格的变化保持一致，材料不会在单元与单元之间发生流动。建立几何模型如图1所示，采用单位制g-cm-μs，取工件长度为15e-2cmX5e-3cm。

图1　切削几何模型

1.2材料模型建立

其中刀具为Rigid模型，刀具材料为；工件选用Johnson-cook模型，Johnson-Cook材料模型是一个能反映应变率强化效应和温升软化效应的理想刚塑性强化模型[3~6]，工件材料为45钢，材料参数见表1。Johnson-cook本构方程如下[4~8]：

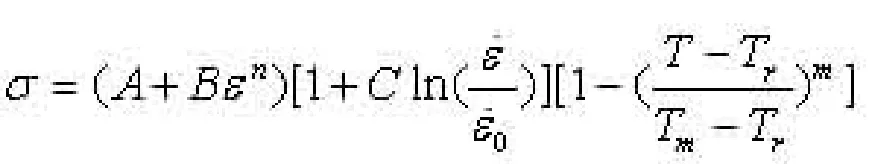
式中，A、B、n、C、m为材料参数；σ为vonMises流动应力；ε为等效塑性应变；为相对等效塑性应变率；为等效塑性应变率；为准静态应变率，取0.001s-1。Tm为材料熔点；Tr为室温。由文献可知，A= 507MPa；B=320MPa；C=0.28；n=0.064;m=1.06;

Johnson-Cook失效准则为：

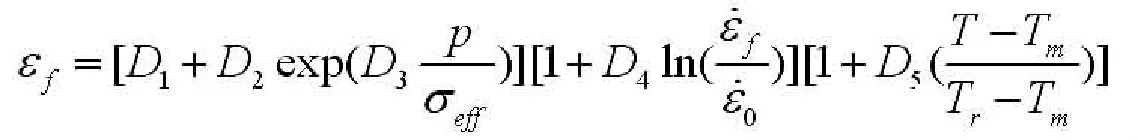
式中，D1、D2、D3、D4和D5为材料参数；为无量纲塑性应变率；p为静水压应力；σeff为von Mises等效应力。

由文献可知D1 =0.15;D2 =0.72;D3 =1.66;D4 = 0.005;D5=-0.84。

表1　工件和刀具材料参数

1.3建立有限元模型

在切削刃附近以及工件表面应力和应变都较其它地方集中，应该采用较密的网格划分，将工件划分为上下两部分，上半部分为切削区。对工件进行网格划分，得到1875个单元，刀具划分为50个单元。

1.4加载边界条件

在切削仿真过程中，工件固定，刀具以某一速度沿某一方向做直线进给，因此对工件有限元模型左端施加X向约束，对工件底部施加X和Y向约束，对刀具则约束其顶端Y方向的位移。刀具与工件接触类型选用LS-DYNA软件提供的侵蚀（ES-TS）接触类型，该接触需要定义目标面与接触面，其中静、动摩擦系数分别为0.15和0.10。假设工件固定不动，刀具以速度v沿X轴负方向相对工件运动了极短的时间t，刀具与工件的相对位置决定了在Y方向上的切深a，两者的相对运动使材料发生破坏并产生切屑，据此侵彻模型来模拟切削过程，进行应力分析。

2　结果分析和讨论

2.1切屑形成过程

1）对于塑性金属进行切削加工时，切屑的形成过程就是切削层金属发生剪切滑移的变形过程。由仿真结果图可见，工件受到刀具切削刃的挤压，处于剪切滑移线左侧的切削层金属被挤压产生弹性变形，而位于剪切滑移线右侧的及其剪切滑移线上的金属产生不可回复的塑性变形，随着切削的进行，塑性变形的材料由切削刃带离工件表面，形成切屑。由此分析，可以将切削过程划分为三个过程：1）弹性变形阶段；2）塑性变形阶段；3）切屑形成阶段。

弹性变形阶段：刀具刚与工件表面开始接触，切削层材料被压缩，发生弹性变形，如果刀具退出，变形亦可回复。此阶段产生的最大等效应力主要集中在刀尖接触区，如图2所示。

图2　弹性变形阶段应力云图

2）塑性变形阶段：刀具继续前进，切削层材料被进一步压缩并沿切削刃向上隆起，此时应力继续增大，逐渐达到弹性极限，材料发生不可回复的塑性变形，如图3所示。

图3　塑性变形阶段应力云图

3）切屑形成阶段：刀具继续前移，最初发生剪切滑移的材料在刀具与后续进入第一变形区域[1]的工件材料共同挤压下形成切屑，此时刀尖将隆起的切削层材料带离工件表面，形成已加工平面。如图4，5所示，此时最大等效应力达到峰值，而后此值将趋于稳定，表明金属切削进入稳定切削状态。

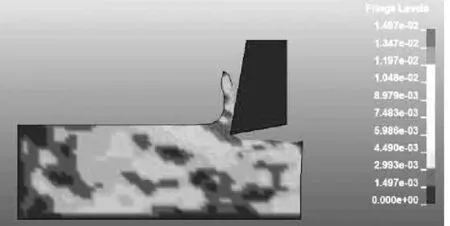
图4　稳定切削阶段应力云图

图5　最大等效应力变化曲线图

如图6所示，由仿真结果得到，切削的结果得到的是带状切屑，这是由于切削厚度较小，切削速度较高，刀具前角较大。根据试验情况，改变切削条件也可以得到崩碎状切屑和挤裂状切屑。

图6　带状切屑

2.2不同切削深度的最大等效应力变化情况

在分析金属切削过程时，我们取工件表面以下不同深度的A单元和B单元（其中B单元处于A单元以下），分析它们是否具有不同的最大等效应力，如图7所示，图中A单元和B单元分别具有不同的切削深度，它们的最大等效应力都是急剧增大到某一值（迅速进入屈服阶段），进入稳定切削阶段，此后，最大等效应力值将稳定处于此值附近波动，经比较，结果显而易见，B单元的应力平均值明显低于A单元。

图7　不同深度单元应力变化曲线

2.3不同切削速度对于最大等效应力的影响

在切削仿真中，我们引入不同的切削速度，以此仿真其对最大等效应力的影响。经过仿真发现，如图8所示，随着切削速度的增大，切削区的最大等效应力显著增大。

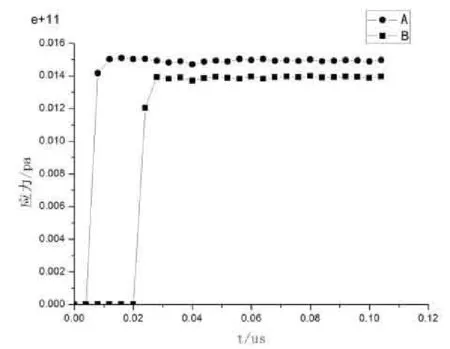
图8　不同切削速度应力变化曲线

3　结论

1）切屑的形成包括三个阶段，即弹性变形阶段、塑性变形阶段、剪切滑移阶段。

2）切屑的分离机理是工件上处于刀尖两侧的较大的且方向相反的剪切力迫使切屑与工件分离。

3）切削初始，最大等效应力急剧增大至材料的屈服极限，随着切削过程的继续，切削层材料被带离工件表面，达到稳定切削状态时，最大等效应力稳定于某一固定值附近。

4）切削深度增大时，最大等效应力将相应的增大。

5）切削速度越大，最大等效应力越大。

6）有限元仿真可以模拟各种工况的切削变形过程，且直观明了。

参考文献：

[1]宿崇,侯俊铭,朱立达,等.基于LS-DYNA的金属切削加工有限元分析[J].东北大学学报(自然科学版),2008(9).

[2]马建斌,李淑娟.基于ANSYS/LS-DYNA的奥氏体不锈钢切削模拟[J].机床与液压,2010(21).

[3] JohnsonGR,CookWH.Fracture characteristics of threemetals subjected to various etrains,strains rates,temperatures and pressures.Engineering Fracture Mechanics,1985,21(1):31-48.

[4]范亚夫，段祝平.Johnson-Cook材料模型参数的实验验定[J].力学与实践，2003，25.

[5]郭磊，吴红兵.高速切削TC4有限元数值模拟研究[J].兵器材料科学与工程，2013，36（2）：88-91.

[6] Ravindra Ambati,Huang Yuan.FEM mesh-dependence in cutting process simulations[J].Adv Manuf Technol,2011,53: 313-323.

[7]尚晓江，苏建宇.ANSYS/LS-DYNA动力分析方法与工程实例[M].北京：中国水利水电出版社，2006.

[8]郝好山,胡仁喜,康士廷,等.ANSYS12.0LS-DYNA非线性有限元分析从入门到精通[M].机械工业出版社,2010.

[9]李国和，王敏杰，段春争.基于ANSYS/LS-DYNA的金属切削过程有限元模拟[J].农业机械学报，2007，38（12）：173-176.

[10]李国和，王敏杰，段春争.正交切削淬硬45钢绝热剪切临界条件实验研究[J].大连理工大学学报，2011，51（4）：518-524.

[11]马建斌,李淑娟.基于ANSYS/LS-DYNA的奥氏体不锈钢切削模拟[J].机床与液压,2010(21).

中图分类号：TG115.6+6