高应变率下Ⅱ型应力强度因子的数值模拟

叶　波,　巫绪涛,　胡凤辉,　廖　礼

(合肥工业大学 土木与水利工程学院,安徽 合肥　230009)



高应变率下Ⅱ型应力强度因子的数值模拟

叶波,巫绪涛,胡凤辉,廖礼

(合肥工业大学 土木与水利工程学院,安徽 合肥230009)

摘要:文章采用有限元软件ANSYS/LS-DYNA程序对静态和冲击荷载作用下的含裂纹半圆弯曲(简称SCB)试验进行了数值模拟。根据静态试验的模拟结果,提出了静态荷载作用下的Ⅱ型应力强度因子拟合公式,其计算误差不超过10%。含复合型裂纹动态SCB试验的模拟结果表明:对于含复合型裂纹的动态加载的SCB试验,动态应力强度因子KⅡ随着试样半径R、裂纹倾角β以及相对裂纹长度a/R的变化呈现规律性变化。当相对裂纹长度a/R在0.4～0.6、裂纹倾角β在10°～40°范围内时,可以直接采用静态公式计算KⅡ,相对误差小于10%。

关键词:断裂韧性;冲击荷载;应力强度因子;SCB实验;复合型裂纹

在各类工程结构中,裂纹广泛存在,会导致脆性材料在低于材料强度时发生破坏。而很多情况下裂纹的起裂和扩展都是动态发生的,如建筑物和结构的抗震,大型水电站、地下采场高应力区的岩爆问题等。因此,研究脆性材料在冲击载荷作用下的动态力学性能,特别是与裂纹扩展相关的动态断裂韧性具有重要的工程应用价值。

早期的研究工作大多局限于静态条件下,国际上系统地研究混凝土在冲击载荷作用下的动态力学性能只是近十几年才开始的,其中对材料Ⅱ型断裂韧性的研究更少。文献[1]提出的SCB试验是一种间接测量脆性材料抗拉强度和断裂韧性的实验方法。然而由于其复杂的边界条件,还没有裂尖应力强度因子的解析解,主要研究方法是数值模拟和实验,如文献[2-5]利用半圆弯曲实验的方法配合数值模拟研究了沥青混合料断裂特性;文献[6]利用半圆弯曲试验配合数值模拟测试土体Ⅱ型断裂韧性。为了更好地测量脆性材料的断裂韧性,随后有研究者采用含裂纹或缺口的半圆弯曲(SCB)试样结合有限元模拟得到了静态断裂韧性的计算公式,如文献[7-9]的研究。然而由于惯性效应的存在,大多数脆性材料在试验过程中无法达到应力平衡,所以静态断裂韧性的计算公式在动态加载下的适用范围和可靠性仍然有待研究。

本文在应力强度因子KⅠ的研究基础上,采用类似方法对KⅡ进行了数值模拟和研究分析。首先采用有限元软件ANSYS程序,对静态含裂纹SCB试验进行了数值模拟,结合量纲分析得到了适用于复合型断裂的Ⅱ型应力强度因子KⅡ拟合公式。其次对基于SHPB技术的动态复合型SCB试验进行了数值模拟,分析了试样半径R、相对裂纹长度a/R及裂纹倾角β对Ⅱ型应力强度因子的影响。最后结合数值外插法[10]和静态分析拟合公式分别计算试样裂尖的动断裂韧性KⅡd，给出了静态拟合公式的适用范围。

1静态SCB试验模拟及KⅡ公式拟合

1.1含复合型裂纹SCB试验参数及简图

采用ANSYS软件对静态复合型断裂SCB试验数值模拟时,材料设置为线弹性本构:弹性模量E=30 GPa,泊松比ν=0.25。圆盘半径R=0.05 m,厚度B=0.01 m,支座间距s=60 mm,裂纹相对长度a/R从0.1变化至0.8,裂纹倾角β从0°变化至45°,承受集中荷载为F=9 kN,试验简图如图1所示。

图1　静态复合型加载SCB试验简图

依据图1建立有限元模型,选择单元类型为Solid186六面体实体单元。为了更好地反映裂纹应力奇异性影响,围绕裂尖的单元采用命令KSCON实现退化奇异等参元。其他单元通过映射划分法划分,应尽量使单元形状规则,且单元尺寸尽量不发生突变。应力强度因子采用相互作用积分法[11]计算。

1.2KⅡ公式拟合

根据量纲分析并结合文献[10-14],经过大量计算,选择KⅡ拟合公式形式为:

(1)

其中,F为试样顶部集中荷载;β为裂纹倾角(裂纹与试样中心轴间的夹角);a为裂纹长度;B为试样厚度;R为试样半径;f为拟合函数。

(1)式中的(sin(2β))F/(BR)对应无裂纹SCB试件圆心处沿着裂纹方向的切应力,同时前半部具有应力强度因子的量纲,f为无量纲形状因子。通过观察KⅡ的变化趋势并进行多次尝试,最终采用(2)式的具体形式,即

(2)

通过观察p1和p2随着β的变化规律,决定采用多项式函数拟合p1和p2关于β的函数,具体表达式形式分别为(3)式和(4)式:

(3)

(4)

其中,拟合系数mi、ni分别为:

m1=-5.06,m2=0.48,m3=-0.016,

m4=2.3E-4,m5=-1.21E-6,

n1=-1.96,n2=1.13,n3=-0.049,

n4=8.5E-4,n5=-5.53E-6。

为了拟合方便,将(1)式除以sin(2β),同时将数值模拟所得到的结果也除以sin(2β),拟合效果如图2所示。

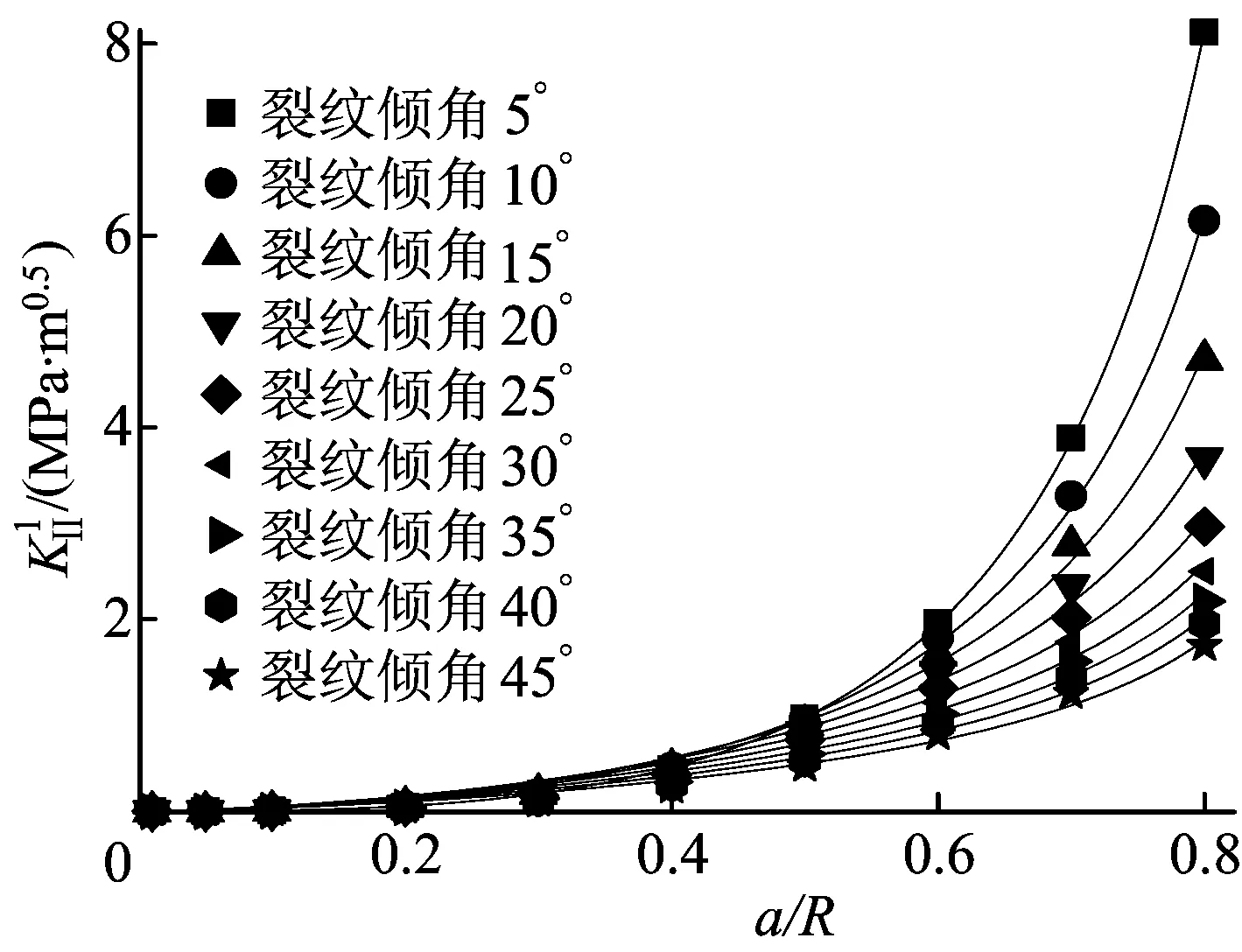
图拟合效果

最大拟合误差小于10%，拟合公式如下：

(5)

2动态加载SCB试验的数值模拟

2.1有限元模型反参数

模拟采用有限元软件ANSYS/LS-DYNA程序,其中试样的本构及相关参数与静态基本相同,圆盘厚度B=25 mm,SHPB装置的入射杆和透射杆采用线弹性本构:弹性模量E=200 GPa,泊松比ν=0.3,密度ρ=7 850 kg/m3,直径100 mm,长度2 000 mm,裂纹相对长度a/R从0.2变化至0.8,裂纹倾角β从5°变化至40°,所用单元类型均采用Solid164六面体实体单元。当β=20°,a/R=0.6时有限元模型如图3所示。

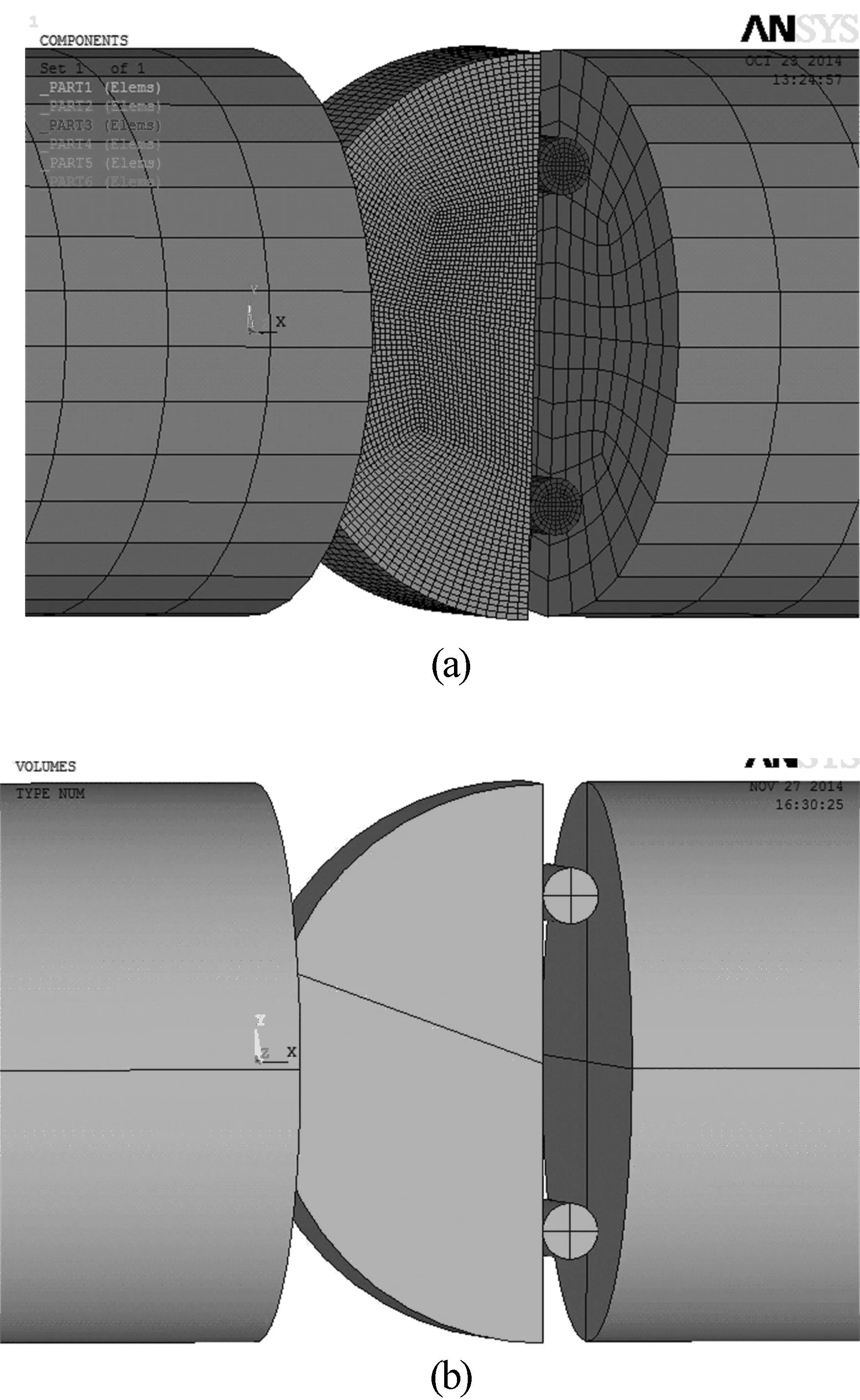
图3　基于SHPB装置的动态SCB试验有限元模型

载荷为加在左端入射杆端面的三角形速度脉冲,由于动态模拟无法实现退化奇异单元,在裂尖附近尽量采用稠密单元,减小单元网格尺寸对结果的影响。

2.2动态复合型加载SCB试验模拟及分析

为了研究R对裂尖实际KⅡd的影响,对不同试样半径下的动态复合型加载SCB试验进行了模拟。图4所示为a/R=0.4,s/R=1.2,试样半径R从50 mm变化至70 mm的KⅡd。

由图4可以得到结论:KⅡd随着半径的增大呈单调递减变化。KⅡd-t曲线在加载过程中均单调增加,而达到峰值后降低并出现震荡。这种震荡正反映了试样应力不平衡导致的惯性效应的影响。为了研究相对裂纹长度a/R以及裂纹倾角β对裂尖实际应力强度因子KⅡd的影响,固定试样半径R=50 mm,支座间距s=1.2R,裂纹倾角由5°变化至40°,每个裂纹倾角下相对裂纹长度a/R由0.2变化至0.8,建立有限元模型进行分析研究。图5所示为裂纹倾角β=30°时不同a/R下KⅡd的变化规律,以及相对裂纹长度a/R=0.4时不同β下KⅡ的变化规律。

图4　不同R下KⅡd变化规律

(a)　不同a/R

(b)　不同β

由于模型过多,为了便于分析,取裂尖实际KⅡd-t曲线加载段的峰值KⅡdmax进行比较。不同a/R情况下KⅡdmax随裂纹倾角β的变化规律、不同裂纹倾角β情况下KⅡdmax随a/R的变化规律如图6所示。

由图6a可以发现,对应相同的裂纹相对长度a/R=0.2～0.7,KⅡdmax随裂纹倾角β的增大而增大,且a/R越大,增大速率越大,KⅡdmax的变化规律与静态模拟结果类似,如图2所示。当a/R大于0.7时变化趋势发生变化。由图6b可以发现,对应相同裂纹倾角β=5°～40°,KⅡdmax随裂纹相对长度(a/R=0.2～0.7)的增大而增大,且裂纹倾角β越大,增大速率越大;β达到30°时,随着裂纹倾角的增大KⅡdmax趋于稳定,变化不明显。

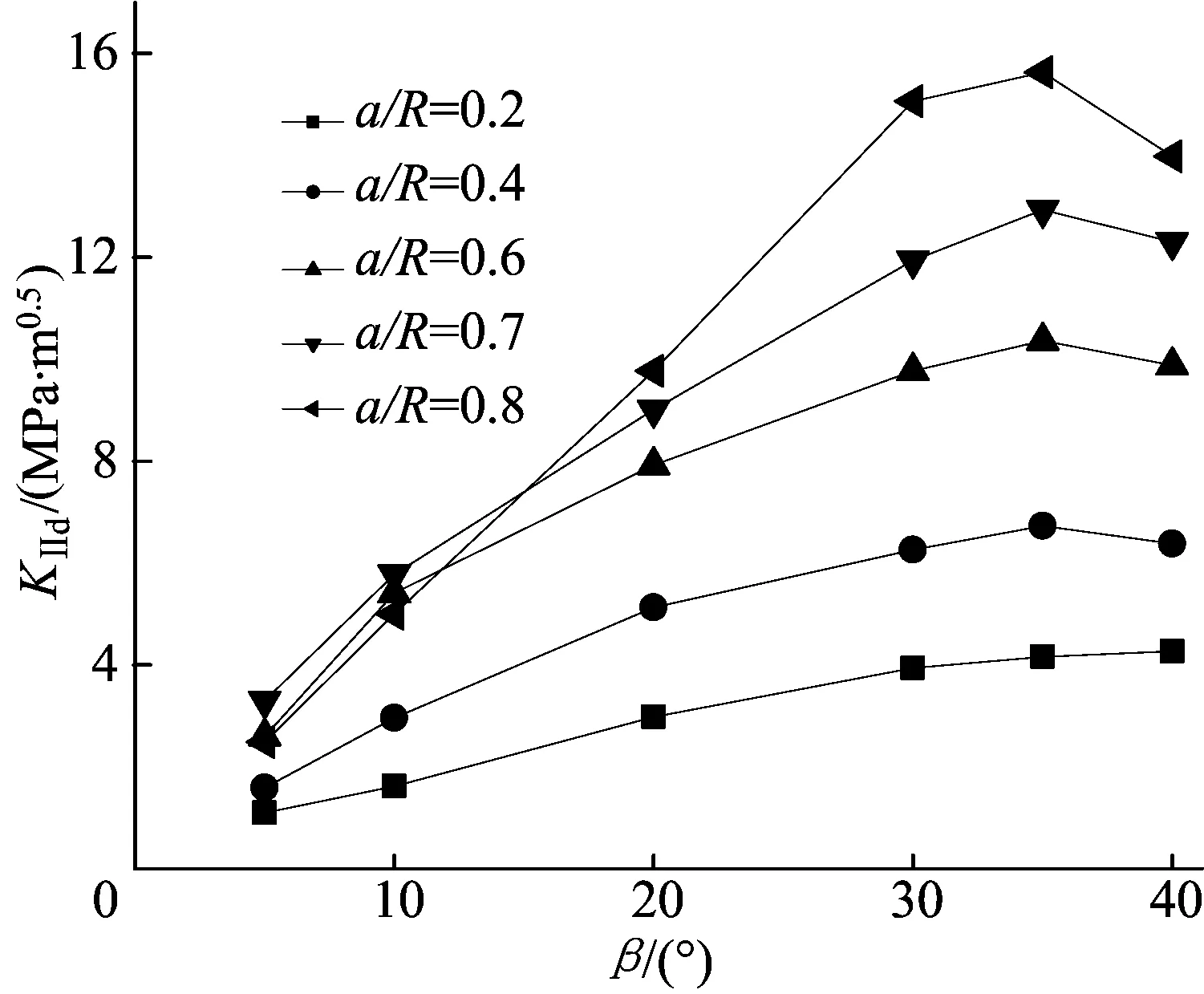
(a)　KⅡdmax随β的变化规律

(b)　KⅡdmax随a/R的变化规律

2.3静态公式的适用范围

由于已经得到了应力强度因子KⅡ的静态计算公式,为了进一步反映静态公式在动态加载下的适用范围,分别采用2种方法计算动态裂尖应力强度因子KⅡd:① 由裂纹面张开位移通过数值外插法[5]得到;②根据试样左右端面的接触力F(t)平均后带入(1)式计算。其中方法①为裂尖实际KⅡd1,方法②为采用静态公式得到的KⅡd2。图7所示为a/R=0.4,β=20°时裂尖实际KⅡd1和静态公式得到的KⅡd2的比较。

图7　a/R=0.4,β=20°时KⅡd1和KⅡd2的比较

为了进一步分析复合加载条件下静态拟合公式的适用性,按(6)式得到不同a/R情况下两者的相对误差C,即

(6)

按(6)式计算了裂尖实际KⅡd1max与静态公式KⅡd2max的相对误差C,见表1所列。其中KⅡd1max和KⅡd2max皆为对应KⅡd1-t曲线加载段的峰值。可以看出,当裂纹倾角β=10°～40°,裂纹相对长度a/R在0.4～0.6之间时,静态公式的相对误差小于10%,精度较高,而超出此范围,相对误差变化不稳定,部分增大至20%～50%,即静态公式失效。

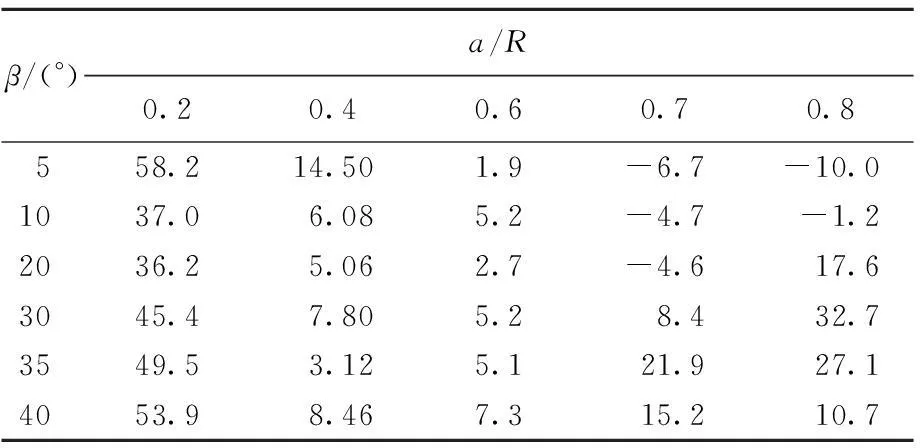
表1　复合型加载下静态公式计算KⅡdmax的相对误差　　%

3结论

本文在应力强度因子KⅠ的研究基础上,采用类似方法对KⅡ进行了数值模拟和研究分析,并得到以下结论:

(1) 参考相关文献并根据含复合型裂纹的静态SCB试验的模拟结果,结合量纲分析得到了适合于静态加载条件下裂纹倾角β=0°～45°,裂纹相对长度a/R=0.1～0.8范围内的应力强度因子KⅡ的拟合公式,根据拟合效果可知该公式精度较高,拟合误差小于10%。

(2) 对于含复合型裂纹的动态SCB试验,KⅡd随试样半径R增大而减小,同时也证明了试验中惯性效应的存在。

(3) 对于含复合型裂纹的动态SCB试验,当裂纹相对长度a/R=0.2～0.7,KⅡd随裂纹倾角β的增大而增大;当β=5°～40°,KⅡd随a/R(0.2～0.7)的增大而增大,当β达到30°后,随着β的增大KⅡd趋于稳定,变化不明显。

(4) 通过采用位移外插法和静态拟合公式计算2种方法得到KⅡd,并计算相对误差发现,对于含复合型斜裂纹的动态SCB试验,在a/R=0.4～0.6,β=10°～40°范围内,也可以直接采用静态公式计算KⅡdmax,相对误差小于10%。

[参考文献]

[1]Chong K P,Kuruppu M D. New specimen for fracture toughness determination for rock and other materials[J]. International Journal of Fracture,1984,26(2): 59-62.

[2]曹轲铭.沥青混合料半圆弯拉试验方法研究[D].长沙:湖南大学, 2007.

[3]刘宇,张肖宁,邹桂莲.基于半圆试件的沥青混合料疲劳裂纹扩展分析[J].科学技术与工程,2009,9(19):5712-5716.

[4]刘宇.基于半圆弯曲试验的沥青混合料动态响应及断裂性能研究[D].哈尔滨:哈尔滨工业大学,2009.

[5]刘宇,张肖宁,王端宜.沥青混合料裂纹扩展阶段的疲劳寿命预测[J].华南理工大学学报:自然科学版,2008,36(2):41-47.

[6]邓文杰,王俊杰,张慧萍.土体Ⅱ型断裂韧度测试方法研究[J].水利水运工程学报,2012(3):64-69.

[7]Ayatollahi M R,Aliha M R M,Hassani M M.Mixed mode brittle fracture in PMMA:an experimental study using SCB specimens[J].Materials Science and Engineering A,2006,417:348-356.

[8]Ayatollahi M R,Aliha M R M.On determination of mode II fracture toughness using semi-circular bend specimen[J].International Journal of Solids and Structures,2006,43(17):5217-5227.

[9]Aliha M R M,Ayatollahi M R.Mixed mode I/II brittle fracture evaluation of marble using SCB specimen[J].Procedia Engineering,2011,10:311-318.

[10]巫绪涛,杨伯源.数值外插法求解空间裂纹应力强度因子的研究[J].合肥工业大学学报:自然科学版,1999,22(4):26-31.

[11]Yau J,Wang S,Corten H.A mixed-mode crack analysis of isotropic solids using conservation laws of elasticity[J].Journal of Applied Mechanics,1980,47(2):335-341.

[12]Chen R,Xia K W,Dai F,et al.Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing[J].Engineering Fracture Mechanics,2009,76(9):1268-1276.

[13]Dai F, Xia K W.Rate dependence of the flexural tensile strength of Laurentian granite[J].International Journal of Rock Mechanics and Mining Sciences,2010,(3):469-475.

[14]Dai F,Xia K W.Determination of dynamic rock mode-I fracture parameters using cracked chevron notched semi-circular bend specimen[J].Engineering Fracture Mechanics,2011,78(15):2633-2644.

(责任编辑张镅)

Numerical simulation of Ⅱ type stress intensity factor under high strain rate

YE Bo,WU Xu-tao,HU Feng-hui,LIAO Li

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:Finite element software ANSYS/LS-DYNA program was used in the numerical simulation of semi-circular bending(SCB) test with crack under static and impact loading. According to the simulation result of static test, the fitting formula of Ⅱ type stress intensity factor under static loading is put forward and the maximum error is less than 10%. The simulation result of dynamic SCB test with mixed-mode crack shows that for the SCB test with mixed-mode crack under dynamic loading, the dynamic stress intensity factor KⅡshows regular changes with the change of specimen radius R, crack angle β and relative crack length a/R. When the relative crack length a/R is from 0.4 to 0.6 and the crack angle β is from 10° to 40°, KⅡis calculated with the static fitting formula and the relative error is less than 10%.

Key words:fracture toughness; impact loading; stress intensity factor; semi-circular bending(SCB) test; mixed-mode crack

中图分类号:O347.4

文献标识码：A

文章编号：1003-5060(2016)02-0239-05

Doi:10.3969/j.issn.1003-5060.2016.02.018

作者简介：叶波(1991-),男,安徽芜湖人,合肥工业大学硕士生;巫绪涛(1971-),男,安徽合肥人,博士,合肥工业大学副教授,硕士生导师.

收稿日期：2014-12-07；修回日期：2015-03-09