含生热体三角腔自然对流数值模拟
2016-04-12王瑞,高才,2
王 瑞, 高 才,2
(1.合肥工业大学 机械与汽车工程学院,安徽 合肥 230009; 2.合肥工业大学 美乐柯制冷技术与工程研究院,安徽 合肥 230009)
含生热体三角腔自然对流数值模拟
王瑞1,高才1,2
(1.合肥工业大学 机械与汽车工程学院,安徽 合肥230009; 2.合肥工业大学 美乐柯制冷技术与工程研究院,安徽 合肥230009)
摘要:文章对内置等温生热体的三角形腔体内空气自然对流换热进行数值模拟。生热体为矩形,位于垂直边上,且温度恒定,三角形斜边的边界温度恒定且低于生热体温度,其余两边绝热。通过有限元方法对不同瑞利数(Ra)下的不同高宽比三角形腔体进行分析,得出腔体内空气的流线图、等温线分布图以及生热体表面空气的努塞尔数Nu与Ra的关系。结果表明,随着Ra的增加,腔内空气自然对流方式由层流向湍流转变,主要的传热方式由热传导转变为对流换热,且较小的高宽比更利于腔内流动和传热。
关键词:自然对流;等温生热体;三角形腔体;瑞利数;传热
在不同的几何腔体内自然对流流动和换热已经成为许多工程研究的主题,这些研究包括各种技术的应用,如太阳能收集器、建筑采暖通风、空气制冷设备、冷却电子设备等。由于有些设备表面倾斜,所以生热体电路元件是位于三角形腔体中,属于突出电子生热体在非矩形附件中工作,如电脑、显示器或电视机等。
文献[1]研究了生热体置于直角三角形腔体底边的自然对流情形,发现生热体的位置和形状对腔内空气流动、温度场和热传递影响显著,要获得更好的散热效果,必须选择更大的长宽比且生热体必须位于底边中心;文献[2-3]研究了三角形截面的斜屋顶在夏天和冬天时自然对流情形,发现三角形截面高与底的比值、瑞利数和温度边界条件对温度场和流场的分布有重要影响;文献[4]研究了不同高度腔体的自然对流情形,发现随着生热体高度的增加,平均努塞尔数也增加,且其位置比传热对流体的流动影响更大;文献[5]研究了部分腔体中自然对流流动情况,发现平均努塞尔数随着腔体高度的增加而减少。这些计算结果为研究三角形腔体内的流动和传热奠定了重要基础。
国内研究中,文献[6]对封闭三角形通道内的热管与壁面的散热问题进行了数值模拟,得出了封闭腔内空气自然对流换热的温度场和速度场,并找出了三角形通道内的换热规律,验证了数值模拟的正确性;文献[7]对不同形式的二维方腔进行了数值模拟,找到了不同的高宽比例对自然对流换热影响的规律;文献[8-10]对封闭腔内层流自然对流换热进行了各种瑞利数条件下的模拟研究,总结了流态转捩时所表现的数值模拟方面的某些现象规律,这对于其他类型腔体换热分析有重要的参考价值。
内含生热体的方腔对流换热问题因具有明确的应用背景而被给予了特别关注,对于三角腔自然对流,文献[1]研究了突出生热体位于腔体底部的情形,而生热体位于其他位置的研究很少。实际情况下,腔体内生热体位置多变,对流动和换热规律的影响还没有被系统地认识。
本文拟研究生热体位于三角腔垂直边的情形,与已有文献进行对比,以了解腔内空气流动和换热规律。
1问题描述与求解
1.1几何模型与控制方程
直角三角形腔体几何模型和网格划分如图1所示,其底L、高H均绝热,斜边保持恒温Tc。侧边矩形生热体宽w,高h,维持恒温Th(Th>Tc),c为生热体在侧边位置。定义AR=H/L,为直角三角形高宽比。
描述该物理模型的无量纲方程组为:


(1)
(2)
其中,X、Y为无量纲坐标;ψ为流函数;Ψ为无量纲流函数;Pr为普朗特数;ω为涡量;Ω为无量纲涡量;θ为无量纲温度;u、v为轴向和径向速度;U、V为无量纲轴向和径向速度;α为热扩散系数;β为热膨胀系数;ν为运动学黏度;g为重力加速度,Ra为瑞利数。
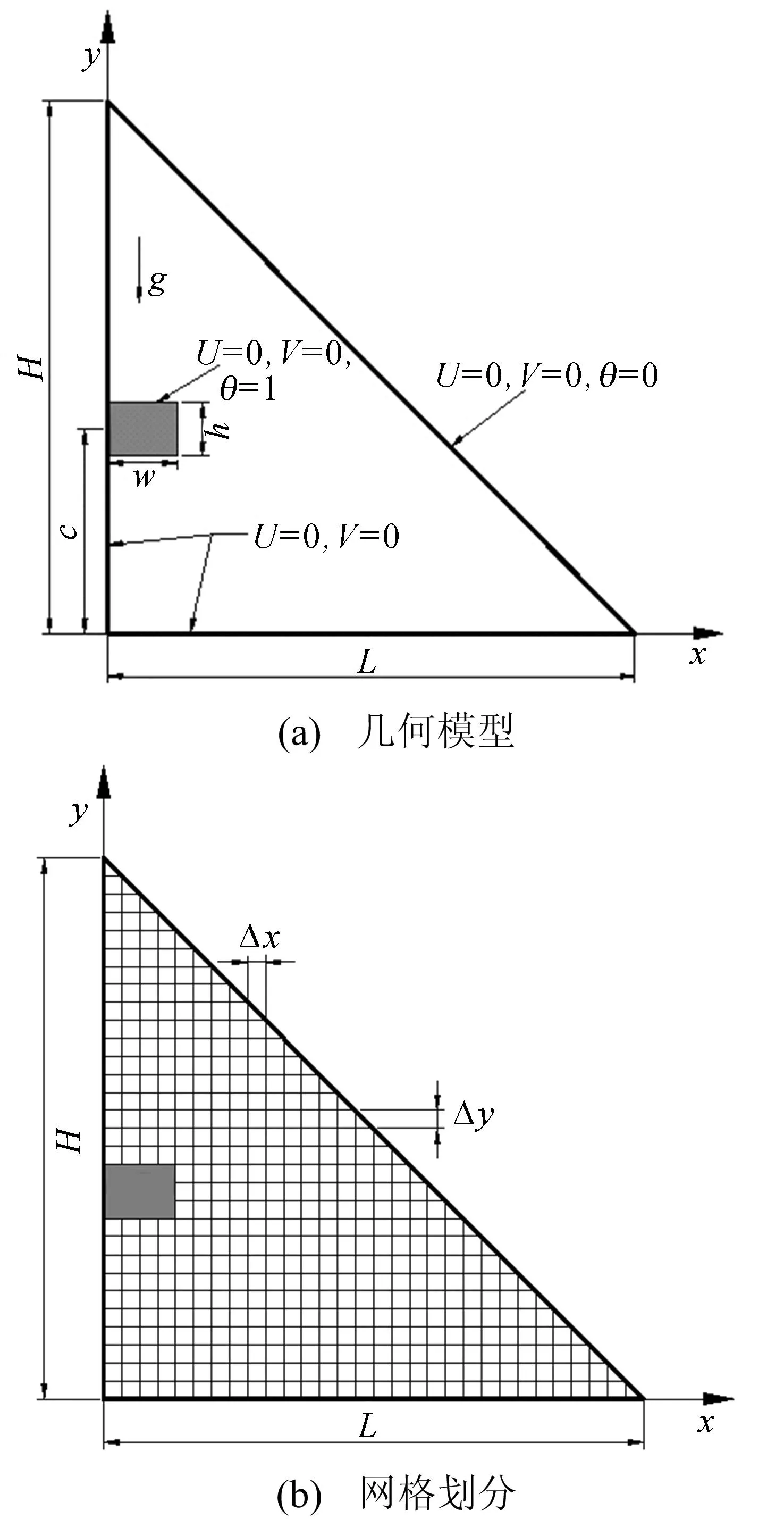
图1 直角三角形腔体几何模型和网格划分
基于上述的无量纲变量,控制方程可以写成:
(3)
(4)
(5)
物理边界条件定义如下:① 斜边上,U=0,V=0,θ=0;② 底边和垂直边上,U=0,V=0;③ 生热体边上,U=0,V=0,θ=1。
平均努塞尔数等于壁面处在壁面法线方向上的流体平均无量纲温度梯度,其大小反应平均对流换热的强弱。在生热体和斜边间传递的热量用局部努塞尔数计算,整合生热体3条边的局部努塞尔数计算出平均努塞尔数。
局部努塞尔计算公式为:
(6)
其中,n为边的方向。生热体边的平均努塞尔数和面平均努塞尔数的计算公式分别为:
(7)
(8)
1.2求解控制
采用ANSYS软件的CFD模块(Flotran)进行二维稳态数值模拟,选取141单元。经反复试验选用60等分L边和60等分H边,其求解精度满足要求且计算速度较快。
腔内流体为空气,普朗特数Pr=0.71,视为不可压缩流体,满足Boussinesq假设[11]。壁面速度满足无滑移条件,压力控制采用TDMA模式,只有介质密度允许变化,其他物性参数保持恒定。忽略辐射换热,重力加速度设定为y轴负方向。迭代收敛标准为:x轴方向速率10-2m/s,y轴方向速率10-2m/s,压力10-8Pa,温度10-8K,湍流动能10-2J,湍流耗散10-2J。
2数值模拟结果与讨论
当几何模型为AR=1.0,c=H/3,h=H/6,w=L/3时,在不同瑞利数下腔内空气流动情况和无量纲温度分布如图2所示。
由流线图可以看出,空气在靠近生热体热壁处受到加热而向上运动,在靠近斜边冷壁处被冷却而向下运动,这样腔内就产生了涡。在不同的Ra值时,腔内都存在2个涡,均为顺时针旋转,且2个涡中心的无量纲坐标几乎一样。随着瑞利数的增加,涡的转速和涡的范围随之变大,腔内空气的流态将由层流向湍流过渡。由等温线图可以看出,Ra为103~104时,腔内等温线分布较均匀,此时腔内的传热主要方式是热传导;当Ra增加到104~105时,腔体内等温线由规则分布变得复杂,说明腔内对流换热逐渐加强;当Ra为105~106时,替代热传导成为主要传热方式;在斜边和生热体的右边及下边处,等温线分布密集,表明这些地方热流密度较大,而生热体的上边则等温线稀疏。在生热体与斜边的热冷壁面附近的薄边界层内始终保持平整,这说明热斜边与生热体的冷壁面附近的传热方式还是热传导。
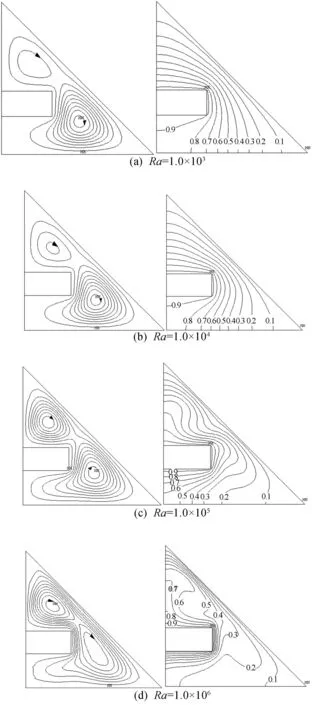
图2 不同瑞利数下的流线图(左)和等温线图(右)
根据文献[1]给出的生热体位于三角腔底边时的流函数变化情况,整理出AR=1.0时的极值,与本文计算值对比,结果见表1所列。由表1可以看出,流函数的最大值max和最小值min(绝对值)均随着瑞利数增大而增大,说明瑞利数增大,腔内空气流动变得剧烈,而本文的计算结果均小于文献[1]值,说明空气流动速度较小;文献[1]腔内的空气流动有3个明显可辨的涡,其中2个顺时针旋转,1个逆时针旋转,而文本仅有2个涡,均为顺时针。由此可以看出生热体的位置对于腔内的空气流动影响显著。
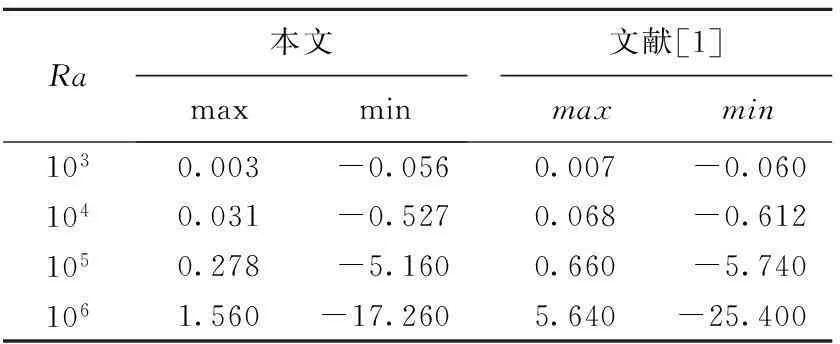
表1 流函数随瑞利数的变化(AR=1.0)
几何模型为Ra=1.0×106,c=H/3,h=H/6,w=L/3,不同高宽比时流线和无量纲温度分布的代表性图示如图3所示。

图3 2种不同宽高比时的流线和等温线
与图2流线图比较可以看出,涡的个数均有明显差异。AR=2.0时,腔内只有1个顺时针涡,且此时腔内流函数值较小(max=1.43);AR=0.5时,腔内共有3个涡,2个顺时针涡和1个逆时针涡,且腔内流函数值较大(max=11.1),空气流动更快,所以对流换热效果更好。由等温线图可以看出温度分布同样紊乱且有较大差异。由此可以看出三角形腔体的形状对腔内空气流动的显著影响。
3种AR值下,生热体各边(上、右、底)Nu值随Ra值变化情况如图4所示。
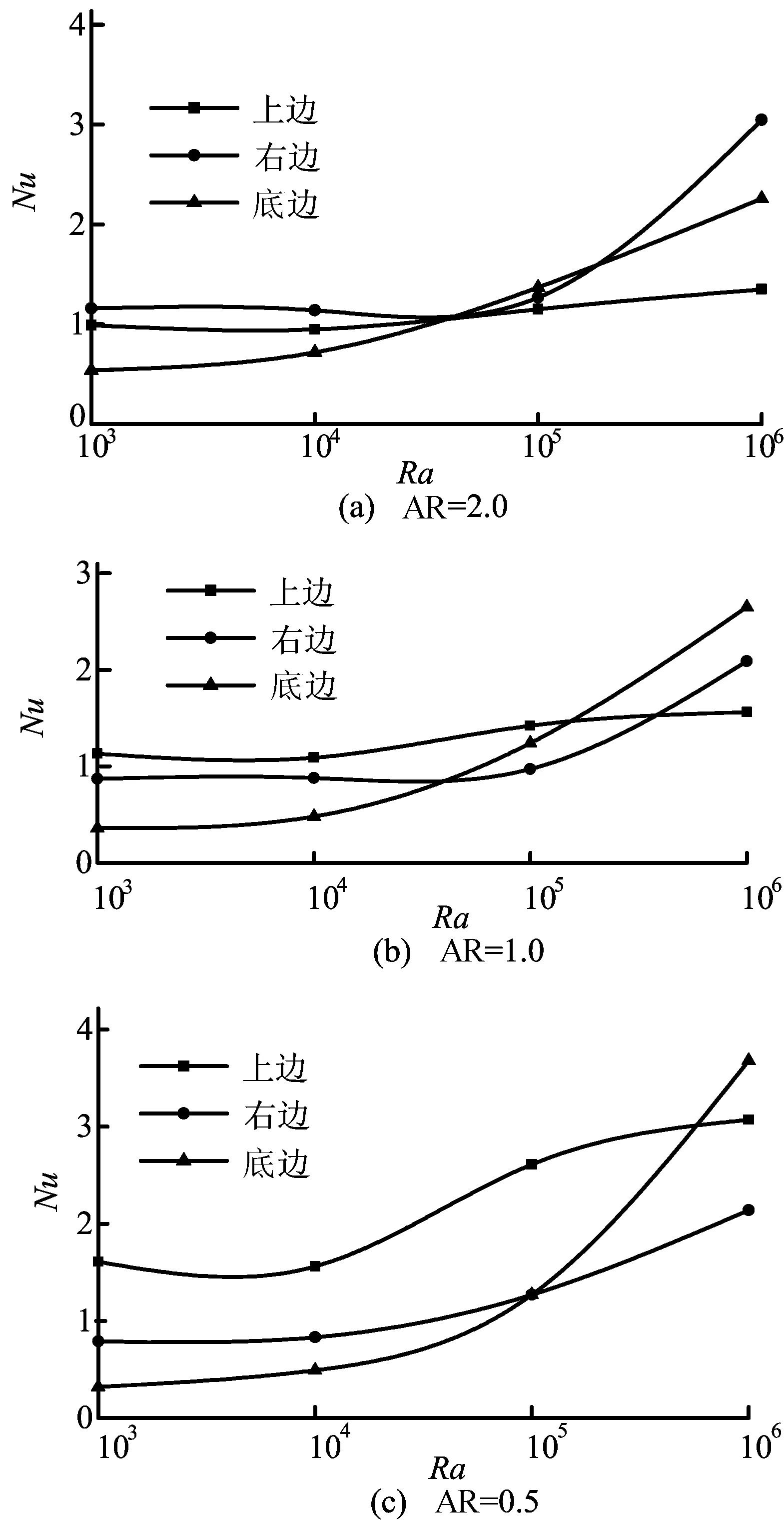
图4 不同AR值下生热体各边的Nu值
由图4可以看出,生热体各边的局部Nu值总体趋势都随着Ra值的增大而增大,但是在同一Ra值域各边增长速率不同,同一条边在不同Ra值域增长速率也不同。上边的局部Nu值在Ra值处于104~105值域时增长最迅速,右边的局部Nu值在Ra值处于105~106值域时增长最迅速,而Ra值在各值域的变化对底边的局部Nu值影响都很显著。
生热体分别置于垂直边和底边[1],不同AR值、不同Ra值时的面平均Nu值如图5所示,其中“AR′”表示文献[1]中生热体位于底边的值,用虚线表示。由图5可以看出,2种情形下各AR值在较低Ra值域时,面平均Nu值的变化缓慢;在较高Ra值域时,面平均Nu值的变化迅速。与文献[1]相比,相同AR值时本文的面平均Nu值在各Ra值域都较低,结合流函数极值的对照结果,原因可理解为突出的侧边生热体对空气流动的阻碍作用比位于底边的情形更显著。本文的3种情形相比,低AR值时Nu值与增长速率都较大,说明较低AR值的直角三角形腔体在不同Ra值域都具有更好的对流传热效果。
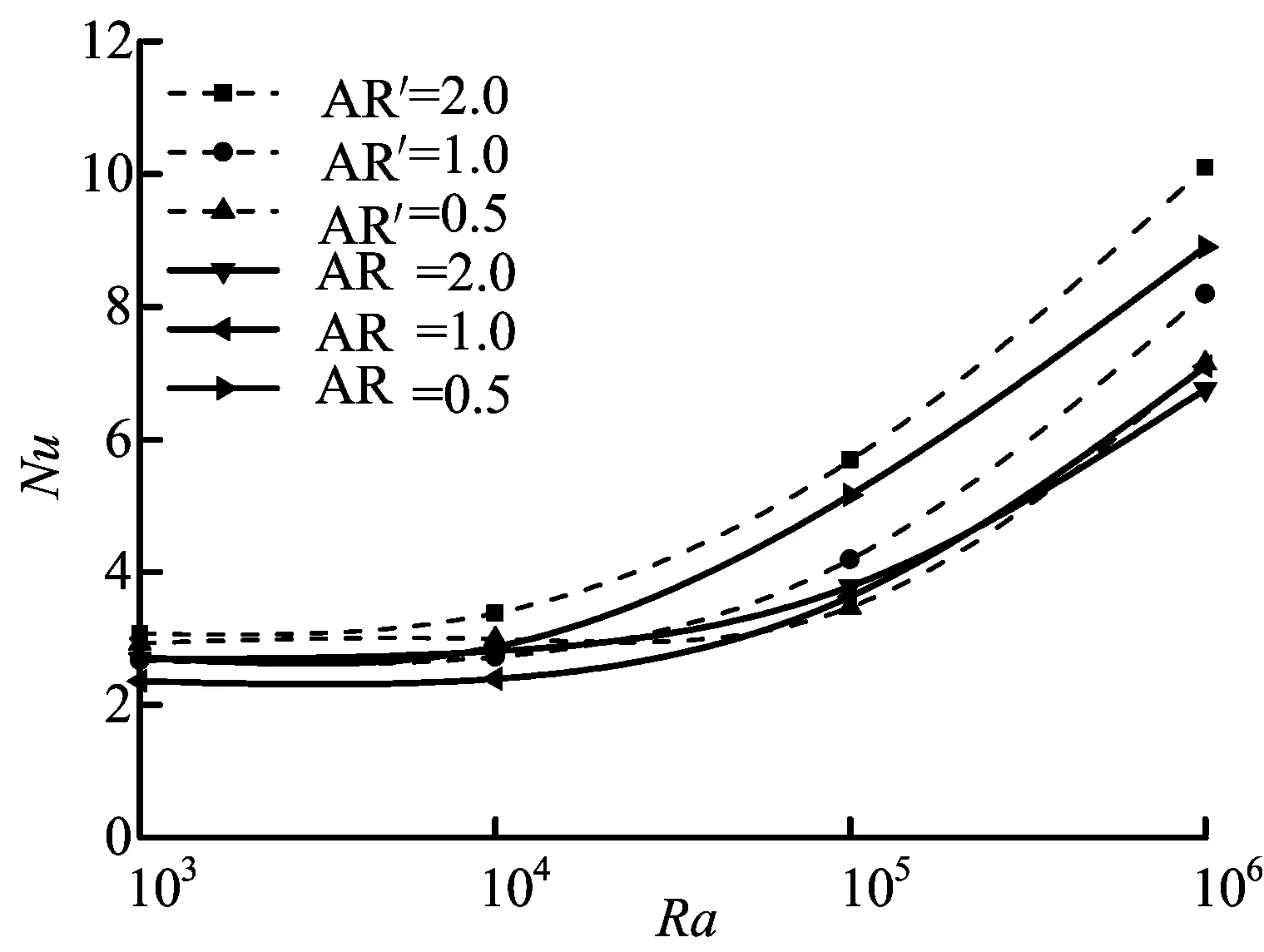
图5 本文与文献[1]各种AR值时的面平均Nu值
3结论
(1) 随着瑞利数Ra的增大,腔内空气对流强度逐渐加强,并且对流强度分布越来越不均匀,封闭腔内自然对流将在Ra处于104~105区间时由层流向湍流过渡。
(2) 生热体各边Nu值随着Ra值的增加而增加,而且Ra值对底边的传热效果影响最为显著。Ra值较小时,传热主要由空气在生热体和冷壁间进行热传导实现,随着Ra值的增大,对流换热逐渐占主导地位。
(3) 在直角三角形腔体内,2条直角边的比例对腔内的流动和温度分布有显著影响,生热体位于垂直边时,较小的高宽比更有利于空气流动,从而获得较大的Nu值及更好的传热效果。
(4) 不同高宽比时,随着Ra值的增大生热体3条边的对流换热效果都有所增强,但Ra值对生热体底边影响最大。
(5) 生热体置于垂直边上时,对空气流动的阻碍效果比置于底边上时更明显,而且相比于生热体的高度,宽度是更为重要的影响因素。
[参考文献]
[1]Varol Y,Oztop H F,Yilmaz T.Natural convection in triangular enclosures with protruding isothermal heater[J].International Journal of Heat and Mass Transfer, 2007, 50(13):2451-2462.
[2]Asan H,Namli L.Laminar natural convection in a pitched roof of triangular cross-section: summer day boundary conditions[J]. Energy and Buildings, 2000, 33(1):69-73.
[3]Asan H, Namli L. Numerical simulation of buoyant flow in a roof of triangular cross-section under winter day boundary conditions[J]. Energy and Buildings, 2001, 33(7):753-757.
[4]Dagtekin I, Oztop H F. Natural convection heat transfer by heated partitions within enclosure[J]. International Communications in Heat and Mass Transfer, 2001, 28(6):823-834.
[5]Yucel N,Ozdem A H.Natural convection in partially divided square enclosure[J].Heat and Mass Transfer,2003,40(1):167-175.
[6]朱义成,王茂盛.封闭三角形通道内热管的自然对流换热研究[J]. 制冷与空调,2009,23(3):83-85.
[7]董韶峰,李荫堂,刘艳华.涡量-流函数法模拟不同高宽比和角度的腔内自然对流[J].低温与特气,2003,21(6):16-21.
[8]秦国良,徐 忠. 谱元方法求解正方形封闭空腔内的自然对流换热[J].计算物理,2001,18(2):119-124.
[9]李光正,马洪林,张宁. 原始变量法计算封闭腔内自然对流[J].华中科技大学学报:城市科学版,2004,21(2):4-7.
[10]李光正,马洪林. 封闭腔内高瑞利数层流自然对流数值模拟[J].华中科技大学学报:城市科学版,2004,21(3):14-17.
[11]张辉,高才,刘向农,等.方腔内不同位置块状食品层流冷却数值研究[J].合肥工业大学学报:自然科学版,2010,33(4):495-497,509.
(责任编辑胡亚敏)
Numerical simulation of natural convection in triangular enclosures with heater
WANG Rui1, GAO Cai1,2
(1.School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China; 2.Meluck Group Academy of Refrigeration Technology and Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract:Natural convection of air in triangular enclosures with isothermal heater was analyzed by numerical simulation. The temperature of the rectangular heater located on the vertical side kept constant. The hypotenuse temperature also kept unchanged, which was lower than the heater, and the remaining sides of the triangle were assumed to be adiabatic. Different triangular cavity aspect ratios under different Rayleigh numbers(Ra) were analyzed by using finite element method. The streamline and isotherm distributions were obtained as well as the relationship between Nusselt number(Nu) and Rayleigh number of the air on the heater’s surface. The results showed that with the increase of Rayleigh number, the laminar natural convection turned into turbulent, and the main way of heat transfer changed from heat conduction to convective heat transfer. It was also found that smaller cavity aspect ratio contributed more effective heat transfer.
Key words:natural convection; isothermal heater; triangular enclosure; Rayleigh number; heat transfer
中图分类号:TB657.5
文献标识码:A
文章编号:1003-5060(2016)02-0161-05
Doi:10.3969/j.issn.1003-5060.2016.02.004
作者简介:王瑞(1989-),男,安徽蚌埠人,合肥工业大学硕士生;
收稿日期:2014-12-16;修回日期:2015-01-20
高才(1974-),男,安徽凤台人,博士,合肥工业大学副教授,硕士生导师.
