一类二次特征值问题的向后误差分析

袁　飞，卢琳璋，李仁仓

( 1．厦门大学数学科学学院，福建厦门361005; 2．贵州师范大学数学与计算机科学学院，贵州贵阳550001; 3．德州大学阿录顿分校数学系，德州阿录顿76019)



一类二次特征值问题的向后误差分析

袁飞1*，卢琳璋2，李仁仓3

( 1．厦门大学数学科学学院，福建厦门361005; 2．贵州师范大学数学与计算机科学学院，贵州贵阳550001; 3．德州大学阿录顿分校数学系，德州阿录顿76019)

摘要:在高速列车的振动分析中，会遇到一类二次特征值问题(λ2AT+λQ+A) z= 0，其中A和Q为n×n复矩阵，且具有如下特殊结构: A和Q都是m×m的分块矩阵，每个块有k×k个元素，即n=m×k;此外，Q是块三对角阵，A只有位于( 1，m)位置的一个块为非零块．本文主要讨论此类二次特征值问题的向后误差，并且证明了矩阵A的误差仅存在于它的非零块A(13)上．

关键词:二次特征值问题;非线性矩阵方程;向后误差;高速列车振动分析; doubling算法

本文中考虑二次特征值问题P(λ) z= 0的向后误差，其中P(λ)是一个矩阵多项式，λ为常量．

向后误差分析的重要性在于研究算法的稳定性和质量，它与向前误差、条件数之间有如下关系:

向前误差≤向后误差×条件数．

由此不等式可以看出向后误差与条件数对于数值结果的误差估计具有重大意义．

扰动理论和向后误差分析有广泛应用，如:线性系统［1］、最小二乘问题、一般特征值问题和广义特征值问题［2－3］，以及物理学中的过阻尼物理系统［4－5］．近年来有很多文献对向后误差的概念进行了阐述［2－3，6］，文献［1］给出了线性系统的向后误差分析，文献［2－3］将向后误差分析推广到了多项式特征值问题，文献［5，7］介绍了特殊矩阵的向后误差．

二次特征值问题在许多领域有丰富的应用［8－12］，如汽车制动系统中的有限元系统［10］、地震工程［8］、保守结构系统和非保守结构系统分析［11－12］，以及最小二乘问题［9］等．但是二次以上特征值问题的向后误差分析并没有很好地得到解决，很多问题难以求出向后误差的值．

本文研究的是铁轨在高速列车通过时的振动问题的有限元模型中产生的二次特征值问题［13－15］．该问题对文献［16］的对称多项式特征值问题以及后来的文献［17－21］有很大的推动作用．文献［17］为该问题建立了有限元模型，文献［22］中已经对该问题提出一种精度很高的保持特征值结构的doubling算法，文献［23－24］对该算法进行改进，减少计算量和计算时间．

本文将要讨论文献［23］中提出的此二次特征值问题的算法的向后误差．首先介绍向后误差的一些基本定义和定理，随后将会给出针对文献［23］中算法的向后误差，最后我们会简要地证明矩阵A的误差只存在于它的非零块A13上．

1相关定义定理

1. 1一些定义

本文中引用了参考文献［6］中的向后误差的定义．

考虑如下非线性特征值问题:

其中矩阵P(λ)的元素为含λ的多项式．

把P(λ)写为如下形式:

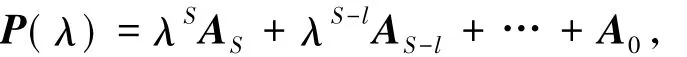
其中At∈Cn×n，l=0: s，我们称P为λ－矩阵［4］．

在本文中，矩阵El( l=0: s)为任意矩阵，用来表示At的误差ΔAl的大小．为了方便表示，令:

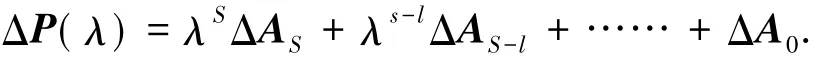
对于复数λ，令:

参考文献与［3］相同，本文中使用的2-范数定义为‖x‖2= ( x×x)(1/2)，‖A‖2= max‖Ax‖2:‖x‖2= 1}．

1. 2向后误差

对于方程( 1)的一对近似解(~x，~λ)，定义向后误差η(~x，~λ)如下:

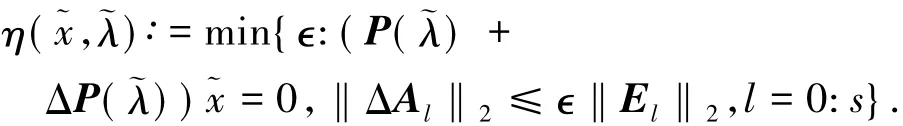
在这个定义下，η(~x，~λ)可由文献［6］中的定理求出．

定理1［6］向后误差η(~x，~λ)可由如下公式求出:

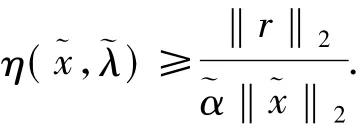
证毕．

从这个定理可以看出，求向后误差的关键在于求出每个‖ΔAl‖2对应的上界∈‖El‖2．

2高速列车振动分析问题的向后误差

2. 1高速列车振动分析问题

在高速列车的振动分析［22-24］中，P(λ) =λ2AT+λQ +A，所求方程为:

A和Q为n×n复矩阵，且具有如下特殊结构:

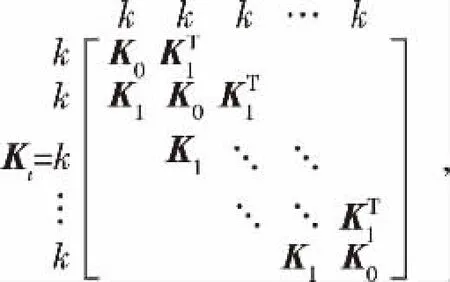
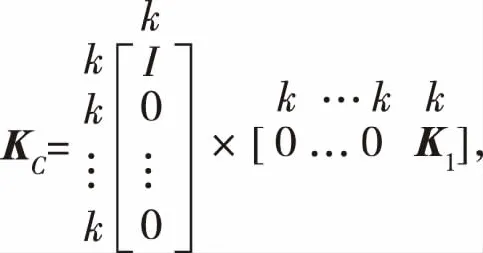
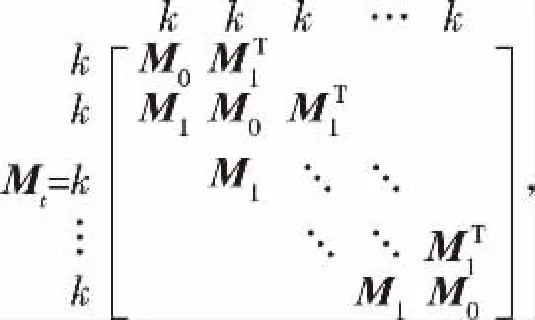
其中i为虚数单位，ω＞0为外力的频率，Kt，Dt，Mt，KC，DC，MC都是m×m的分块实矩阵，每个块有k×k个元素．A和Q都是m×m的分块矩阵，每个块有k× k个元素，即n = m×k;此外，Q是块三对角阵，A只有位于( 1，m)位置的一个块为非零块A13．

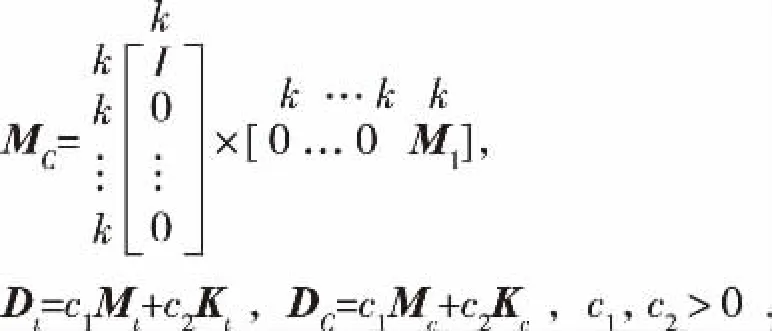
我们简单地介绍文献［23］中的求解步骤:

1)计算方程

的稳定解Φ，使得ρ(Φ－1A)＜1．

2)利用步骤1中求出的Φ对P(λ)进行分解:

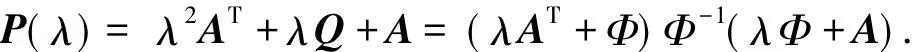
3)由于λAT+Φ和λΦ+A的特征值互为倒数，且λΦ+A对应所有模小于1的特征值，所以只需利用步骤1)中求出的Φ求出λΦ+A的特征值和特征向量，再求出这些特征值的倒数对应的特征向量即可．

在文献［23］中，我们详细介绍了高速列车振动分析问题的求解过程和数值结果，本文主要讨论该问题的向后误差．

2. 2求该问题的向后误差

本文研究的铁轨在高速列车通过时的振动问题，其有限元模型中产生的二次特征值问题(λ2AT+λQ+ A) z=0属于回文二次特征值问题，所以在这里我们采用回文特征值问题向后误差的分析方法［21］来分析该二次特征值问题的向后误差．

由于P(λ) =λ2AT+λQ+A，所以我们可以定义A0=A，A1=Q，A2=AT．假设(ξ，ν)是P(λ)的一个近似特征值对，于是这样定义高速列车震动分析问题的向后

误差ΔF:

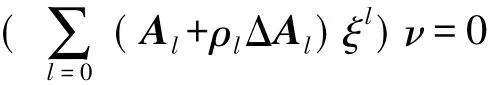
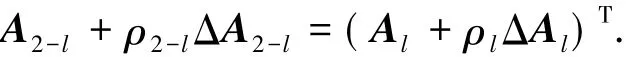
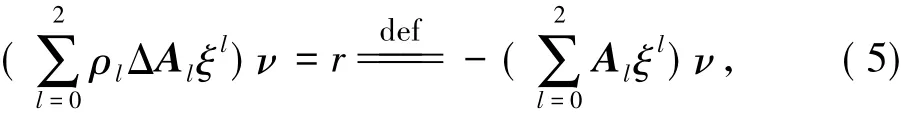
在这里定义了r．

假设Al的阶数n≥2，令Q∈C是酉矩阵，即QQH=ln，使得

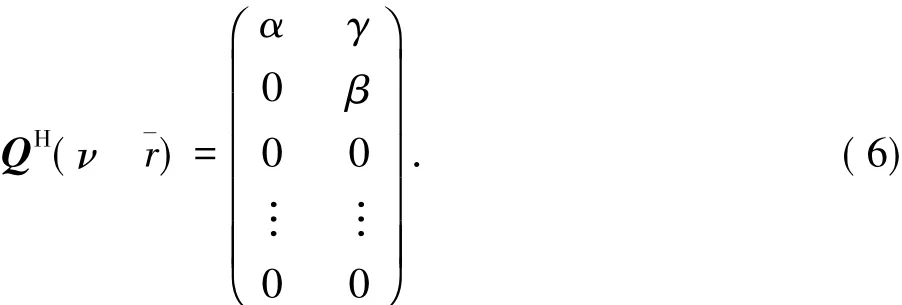
显然这个酉矩阵是存在的，由式( 6)可知

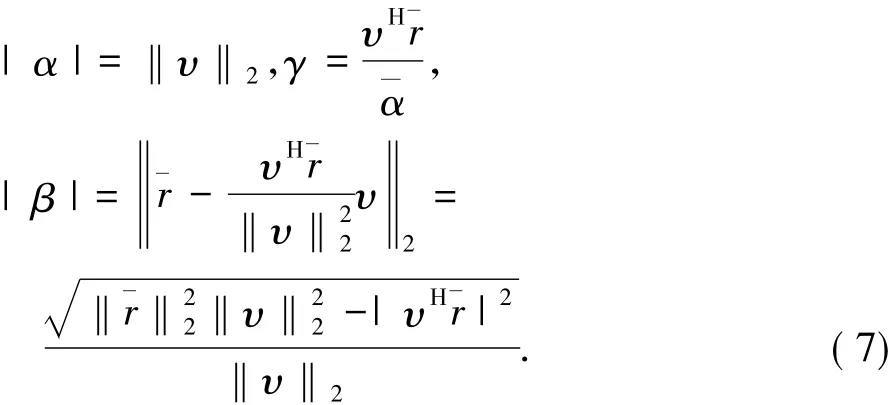
由式( 5)可以得到

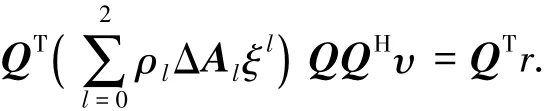
令

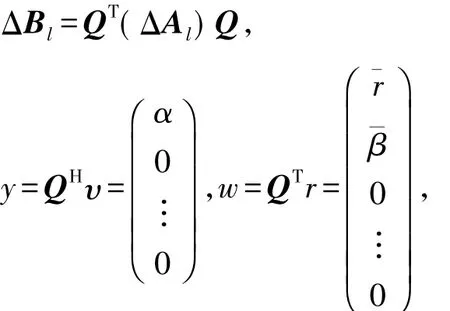
可以得到

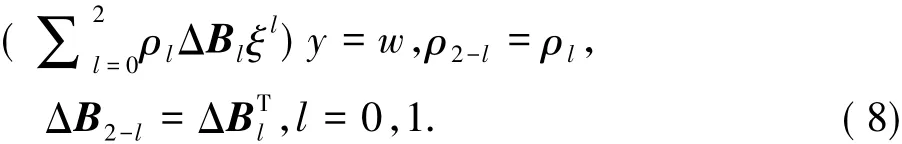
那么高速列车震动分析问题的向后误差ΔF可由如下等式表示:

其中的矩阵ΔB0，ΔB1满足式( 8)．

令

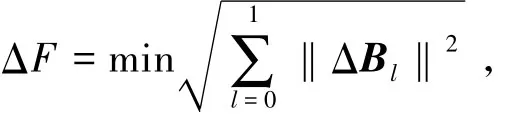
则由式( 7)可知

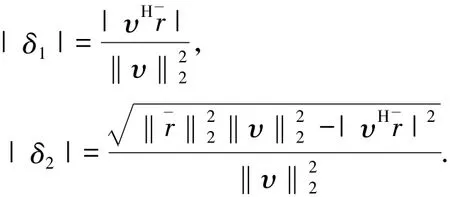
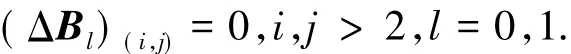
进一步分析可以得出，在ΔBl中除了

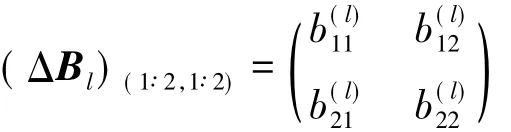
这4个未知量以外，其他元素均为零．

证明方程( 8)可以看作是以ΔBl的元素为未知量的n个方程构成的方程组．观察后发现，后n－2个方程的右边为0，而左边仅包含如下未知量:

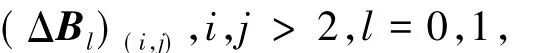
并且这些未知量并没有出现在前两个方程中．

那么对于

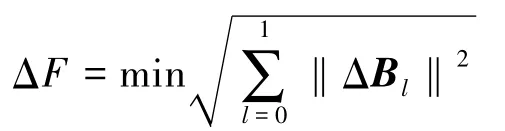
而言，要使得向后误差ΔF达到最小，必然有

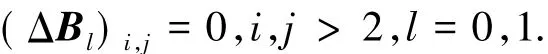
由上述推理可知，只需要考虑方程组( 8)的前两个方程，而这两个方程中仅包含4个未知量:

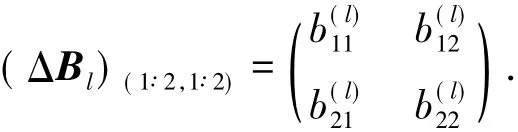
证毕．

由于方程组( 8)中有ρ2－l=ρl，且对于l = 0，1有ΔB=ΔBT，那么可以得到:

2－ll

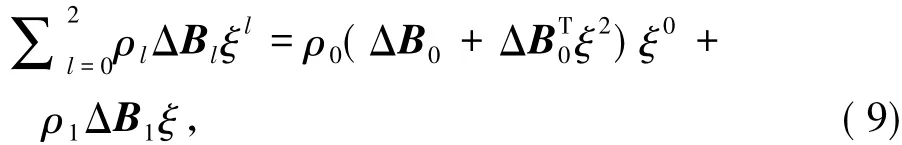
且ΔB1=ΔBT1．

继续定义如下参数:

于是可以得到高速列车震动分析问题的向后误差ΔF．

定理3假设δ1，δ2，Φ，Ψ如上文定义，则对于高速列车震动分析问题P(λ) =λ2AT+λQ+A，近似特征对(ξ，υ)的向后误差ΔF可由如下公式给出:

其中

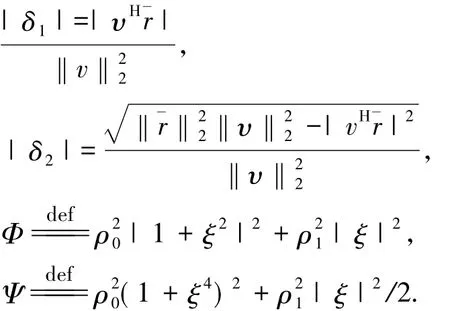
证明结合定理2与等式( 9)，方程组( 8)可以写为如下形式:

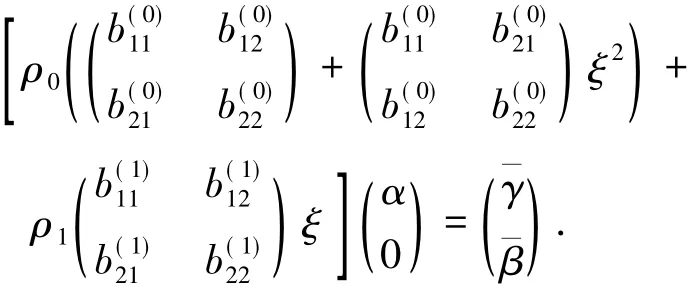
这个方程组可以写为如下两个方程:

观察上述两个方程，可以得到如下结论:

1)由于b2(

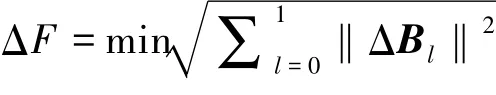
2)方程( 10)和( 11)的未知量不同，是相互独立的两个方程，所以可以分别求出方程( 10)和( 11)的最优解，使得

达到最小．由定理2可以知道这两个多项式之和等于ΔF2．接下来求这两个多项式的最小值．对于方程( 10)，令

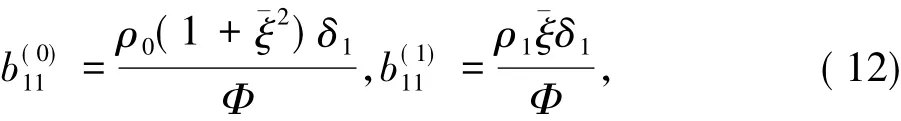
可以验证这样的b( 0)和b( 1)满足方程( 10)．由Cauchy－

1111Schwarz不等式，方程( 10)的任意解b( 0)和b( 1)满足

1111

对于方程( 11)，令

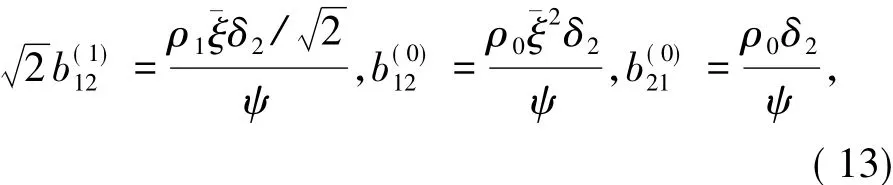
可以验证这样的b(120)，b(210)和b1(21)满足方程( 11)．由Cauchy－Schwarz不等式，方程( 11)的任意解b(120)，b(210)和b(121)满足

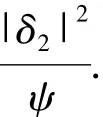
所以

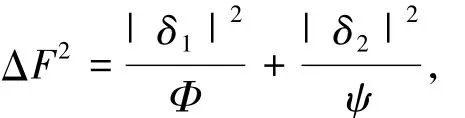
即近似特征对(ξ，ν)的向后误差ΔF可由如下公式给出:

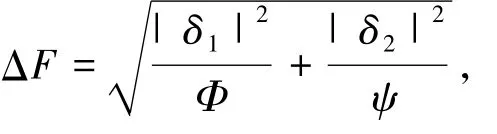
其中

证毕．

2. 3 ΔA的结构分析

由文献［22］中第5部分的等式( 5．2)和( 5．3)可知(ξ，υ)实际上是由Φ，Q和A13同时决定的，即:

由文献［23］中第5部分的等式( 3．4)，( 3．5)和( 3．6)可知Φ是由Q和A13同时决定的，即

综合式( 14)和( 15)可以得到

从式( 16)可以看出矩阵A的误差只存在于它的非零块A13上．

3数值实验

下面给出数值结果，本文使用的矩阵与参考文献［22－24］给出的模型相同．用于数值实验的3个矩阵的大小分别为( k，m) = ( 159，11)，( 303，19)，( 705，51)．系数矩阵A和Q的形式由本文引言部分给出．振动频率ω的值取为1 000．

对于每组系数矩阵A和Q对应的二次特征值问题P(λ) z = 0，我们首先使用文献［23］中的算法求出它的全部近似特征值和特征向量，然后随机从中取出一个近似特征值对(λ，z)，最后使用本文定理3中给出的方法求出了该问题的向后误差(表1) :

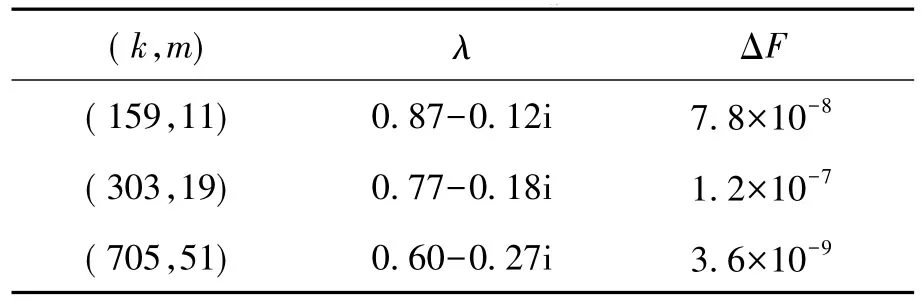
表1数值实验结果Tab．1 Result of experiment

4结论

本文介绍了向后误差相关的概念，并且求出了在高速列车的振动分析［22-24］问题中的向后误差．由于本文研究的二次特征值问题(λ2AT+λQ+A) z = 0属于回文二次特征值问题，所以在这里我们采用回文特征值问题向后误差的分析方法［21］来分析该二次特征值问题的向后误差．在本文的最后，通过对文献［22－24］中计算过程的分析，证明了使用文献［23］中的算法，矩阵A的误差ΔA只存在于它的非零块A13上．对于参考文献［22-24］给出的3个铁轨在高速列车通过时的振动问题的有限元模型，本文给出了一些数值实例，求出了随机一个近似特征值对对应的向后误差．

［1］RIGAL J L，GACHES J．On the compatibility of a given solution with the data of a linear system［J］．Journal of the ACM ( JACM)，1967，14( 3) : 543－548．

［2］FRAYSSE V，TOUMAZOU V．A note on the normwise perturbation theory for the regulargeneralized eigenproblem［J］．Numerical Linear Algebra with Applications，1998，5( 1) : 1－10．

［3］HIGHAM D J，HIGHAM N J．Structured backward error and condition of generalizedeigenvalue problems［J］．SIAM Journal on Matrix Analysis and Applications，1998，20 ( 2) : 493－512．

［4］LANCASTER P．Lambda－matrices and vibrating systems ［M］．Oxford: Pergamon Press，1966: 130－135．

［5］DUFFIN R J．A minimax theory for overdampednetworks［J］．J Rat Mech Anal，1955，4( 2) : 221－233．

［6］TISSEUR F．Backward error and condition of polynomial eigenvalue problems［J］．Linear Algebra and Its Applications，2000，309: 339－361．

［7］STEWART G W，SUN J G．Review of matrix perturbation theory［J］．Linear Algebra and Its Applications，1992，160: 255－259．

［8］GANDER W，GOLUB G H，VON MATT U．A constrained eigenvalue problem［J］．Linear Algebra and Its Applications，1989，114/115: 815－839．

［9］CLOUGH R W，MOJTAHEDI S．Earthquake response analysis considering non－proportional damping［J］．Earthquake Engineering＆Structural Dynamics，1976，4 ( 5) : 489－496．

［10］KOMZSIK L．Implicit computational solution of generalized quadratic eigenvalue problems［J］．Finite Elements in Analysis＆Design，2001，37( 1) : 799－810．

［11］SMITH H A，SINGH R K，SORENSEN D C．Formulation and solution of the non－linear，damped eigenvalue problem for skeletal systems［J］．International Journal for Numerical Methods in Engineering，1995，38( 18) : 3071－3085．

［12］ZHENG Z C，REN G X，WANG W J．A reduction method for large scale unsymmetriceigenvalue problems in structural dynamics［J］．J Sound Vibration，1997，199 ( 2) : 253－268．

［13］HILLIGES A．Numerische lösung von quadratischen eigenwertproblemen mit anwendung in der schienendynamik［D］．Diplomarbeit，TU Berlin: Inst F Mathematik，2004．

［14］HILLIGES A，MEHL C，MEHRMANN V．On the solution of palindromic eigenvalue problems［C］∥Proceedings of the 4th European Congress on Computational Methods in Applied Sciences and Engineering ( ECCOMAS)．Finland: Jyväskylä，2004: 1－10．

［15］IPSEN I C F．Accurate eigenvalues for fast trains［J］．SIAM News，2004，37( 9) : 1－2．

［16］MACKEY D S，MACKEY N，MEHL C，et al．Structured pol－ynomial eigenvalue problems: good vibrations from good linearizations［J］．SIAM Journal on Matrix Analysis and Applications，2006，28( 4) : 1029－1051．

［17］CHU E K W，HWANG T M，LIN W W，et al．Vibration of fast trains，palindromic eigenvalue problems and structurepreserving doubling algorithms［J］．Journal of Computational and Applied Mathematics，2008，219( 1) : 237－252．

［18］HUANG T M，LIN W W，QIAN J．Structure－preserving algorithms for palindromic quadratic eigenvalue problems arising from vibration of fast trains［J］．SIAM Journal on Matrix Analysis and Applications，2009，30( 4) : 1566－1592．

［19］KRESSNER D，SCHRÖDER C，WATKINS D S．Implicit QR algorithms for palindromic and even eigenvalue problems ［J］．Numerical Algorithms，2009，51( 2) : 209－238．

［20］LANCASTER P，PRELLS U，RODMAN L．Canonical structures for palindromic matrix polynomials［J］．Oper Matrices，2007，1( 4) : 469－489．

［21］LI R C，LIN W W，WANG C S．Structured backward error for palindromic polynomial eigenvalue problems［J］．NumerischeMathematik，2010，116( 1) : 95－122．

［22］GUO C H，LIN W W．Solving a structured quadratic eigenvalue problem by a structure－preserving doubling algorithm ［J］．SIAM Journal on Matrix Analysis and Applications，2010，31( 5) : 2784－2801．

［23］LU L，YUAN F，LI R C．A new look at the doubling algorithm for a structured palindromicquadratic eigenvalue problem［J］．Numerical Linear Algebra with Applications，2015，22: 393－409．

［24］LU L，YUAN F，LI R C．An improved structure－preserving doubling algorithm for a structured palindromic quadraticeigenvalue problem［R］．Arlington: University of Texas at Arlington，2014．

Backward Error Analysis for Some Quadratic Eigenvalue Problems

YUAN Fei1*，LU Linzhang2，LI Rencang3

( 1．School of Mathematical Sciences，Xiamen University，Xiamen 361005，China; 2．College of Mathematic and Computer，Guizhou Normal University，Guiyang 550001，China; 3．Department of Mathematics，University of Texas at Arlington，Arlington，TX 76019，USA)

Abstract:In studying the vibration of fast trains，we encounter a palindromic quadratic eigenvalue problem (λ2AT+λQ+A) z=0，where A，Q∈C(n×n)and QT=Q．Moreover，thematrix Q is block tridiagonal and block Toeplitz，and the matrix A possesses only one nonzero block in the upper－right corner．We then discuss the backward error for this problem in this article and prove that the error of A is only on its non－zero block A(13)．

Key words:quadratic eigenvalue problem; nonlinear matrix equation; backward error; vibration high speed train analysis; doubling algorithm

*通信作者:ranma01@ 163．com

收稿日期:2014－12－15录用日期: 2015－05－20

doi:10．6043/j．issn．0438－0479．2016．01．019

中图分类号:O 241．7

文献标志码:A

文章编号:0438－0479( 2016) 01－0097－06

引文格式:袁飞，卢琳璋，李仁仓．一类二次特征值问题的向后误差分析［J］．厦门大学学报(自然科学版)，2016，55( 1) : 97－102．

Citation: YUAN F，LU L Z，LI R C．Backward erroranalysis for some quadratic eigenvalue problems［J］．Journal of Xiamen University ( Natural Science)，2016，55( 1) : 97－102．( in Chinese)