带有分数积分的波动方程解的非存在性

许勇强

( 1．闽南师范大学数学与统计学院，福建漳州363000; 2．厦门大学物理与机电工程学院，福建厦门361005)



带有分数积分的波动方程解的非存在性

许勇强1，2

( 1．闽南师范大学数学与统计学院，福建漳州363000; 2．厦门大学物理与机电工程学院，福建厦门361005)

摘要:通过选择恰当的检验函数与平移讨论相结合，给出了一类非线性项具有非局部性质的波动方程局部解和全局解存在的必要条件．

关键词:波动方程;非线性项;分数积分;全局非存在性;弱解

本文主要研究下面的波动方程

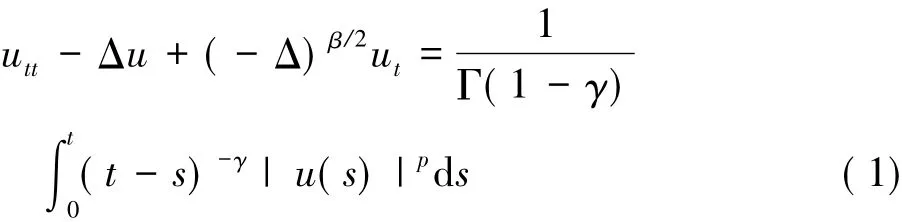
的弱解的非存在性问题．它满足如下的初值条件:

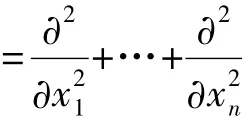
由于下面的极限

在分布意义下存在，所以方程( 1)可以认为是经典的半线性波动方程

的逼近问题，这里Γ是欧拉γ函数．

显然，方程( 1)中的非线性项包含自相似的记忆类型，且可以看作是Riemann－Liouville积分算子

对于该算子，最早于1832年，Liouville引进了α=－∞的特殊情形，然后于1876年，Riemann考虑了α= 0的形式［1］．因而，方程( 1)具有下面的形式:

其中Jα0|t表示Riemann－Liouville分数积分(见公式( 10) )．

我们来描述与方程( 1)相联系的一些方程的存在意义．最近，Chen等［2］研究了下面的方程:

该方程用于描述声音在黏性流体中的传播，其中c0表示无黏性相速度，2α0则代表热力黏性系数．因此，方程( 5)可以看作是早期Greenberg等［3］重要工作的推广．该作者考虑了下面的方程:

其中ρ0，λ表示与介质有关的常数，而g( x，t)则表示外力的一个给定函数．

因为方程( 5)可以认为是非线性方程的逼近问题，所以方程( 3)包含了一个具有应用价值的非线性项．同时，Carvalho等［4］研究了方程( 3)．假如在方程( 3)中取β=0，那么得到了带有线性阻尼项ut的波动方程．许多数学工作者对此做了广泛的研究［5－8］．实际上，文献［5］对方程( 3)作了全面研究，这对应于β= 0的情况．Fino［9］应用文献［5］研究了下面的问题

其中0＜γ＜1，p＞1，( u0，u1)∈H1( RN)∩L2( RN)，这是方程( 1)在β=0的特殊形式．

本文主要考虑0＜β≤2的情形，主要目的是研究方程( 1)在这种情形下的局部解和全局解不存在的必要条件，同时揭示了初值在无穷远处的值对局部解和全局解的存在性具有很深的影响．本文所采用的方法来源于文献［6－7，10－11］．

1预备知识

在这部分，我们将给出有关分数阶拉普拉斯算子、分数积分以及分数导数的相关结果．

首先考虑下面的特征值问题

其中Ω是有界开集．取λk( k=1，2，…，+∞)是－Δ在L2(Ω)中的特征值，φk是λk对应的特征向量，则

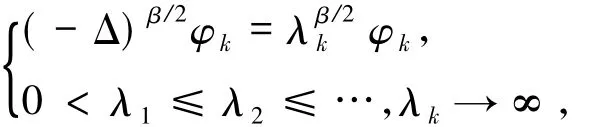
且

所以，对于任意的u，v∈D( (－Δ)β/2)，有下列的性质

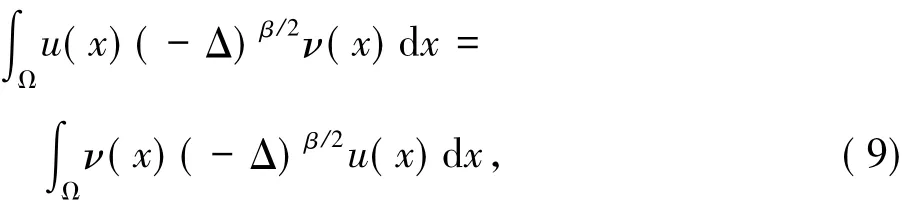
关于更多的细节，可参看文献［12］．

下面来定义Riemann－Liouville分数左右导数．设AC［0，T］表示所有在［0，T］( 0＜T＜∞)上绝对连续的函数空间．如果f∈AC［0，T］，则Riemann－Liouville分数左右导数Dα0|tf( t)和Dαt|Tf( t)可定义如下:

这里f∈Lq( 0，T) ( 1≤q≤∞)，α∈( 0，1)，

表示Riemann－Liouville分数积分［3］．而且对于任意的f，g∈C(［0，T］)，如果Dα0|tf( t)和Dαt|Tg( t) ( t∈［0，T］，0＜α＜1)存在且连续，有下面的分部积分公式［12］:

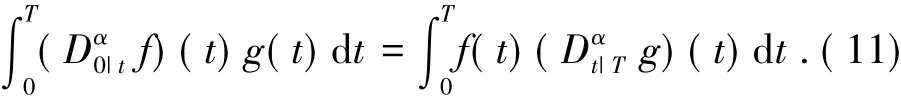
注意到当f∈ACN+1［0，T］且N≥0时，有［12］

其中

∂N表示一般意义下的N次导数．而且对于1≤q≤∞，t下面的公式［12］

在［0，T］上几乎处处成立．

本文将用到下面的结果:

所以有

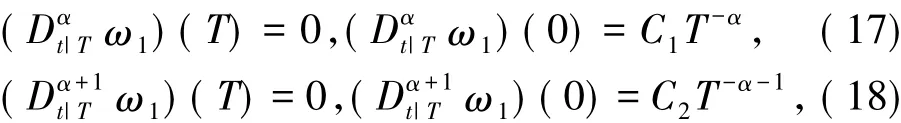
这里

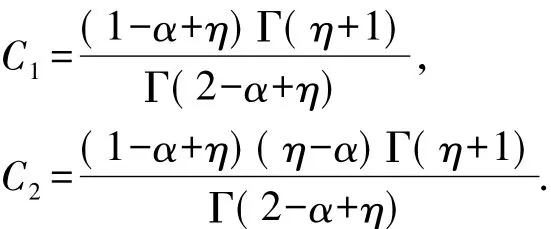
2本文的主要结果

定义1取u∈Lploc( QT)，如果对于任意的检验函

数φ∈C∞0( RN×［0，T］)都有

那么函数u( u∈L1loc( QT) )是方程( 1)的一个弱解，这里φ≥0，0＜T＜+∞，α=1－γ，φ( x，T) =φt( x，T) = 0．

本篇文章的主要结果如下:

定理1取p＞1，0＜β≤2且u0≥0，T＞0．如果

或者

那么问题( 1)没有非负的局部解．

注1根据定理1可估计局部解的存在时间如下:

定理2(全局解的必要条件)取p＞1，1≤β≤2且u0( x)≥0．如果问题( 1)有一个非平凡的全局解，那么存在常数K1，K2和K3使得

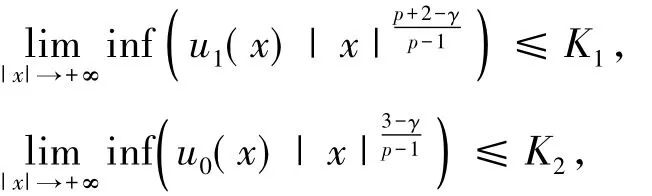
3定理1的证明

现在方程( 1)两边乘以φ，然后在QT=( 0，T)×RN上积分，根据式( 17)和( 18)，得到

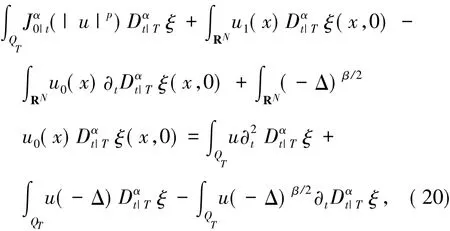
联合式( 13)，( 17)和( 18)，并且考虑到(－Δ)β/2φ1( x/ R) =λβ1/2R－βφ1( x/R)，可推出

这里

为了估计方程( 22)的右边的第一个积分，把它写为下面的形式:

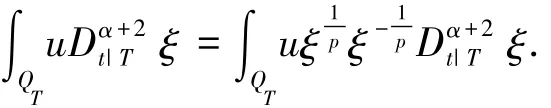
因而，

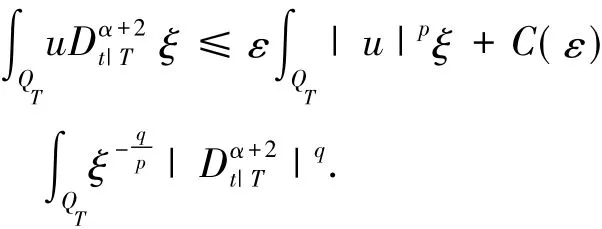
相似地，

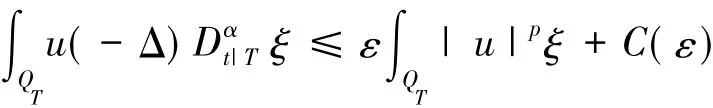
假如3ε=1，易于得到

这时引入变量替换t=τT，x=Ry，然后在式( 23)中联合( 14)，( 15)和( 16)，可推出

这里

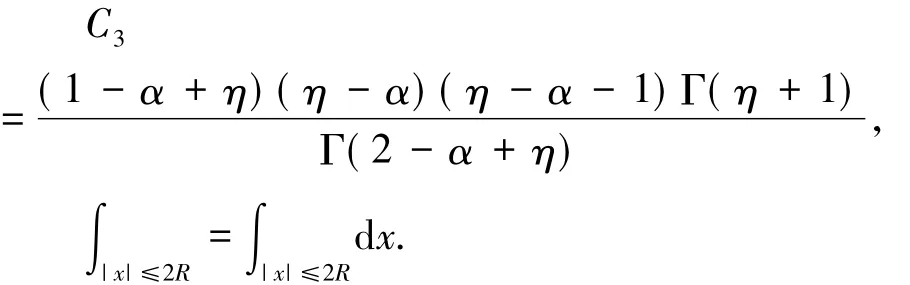
在不等式( 24)中，使用下面的估计

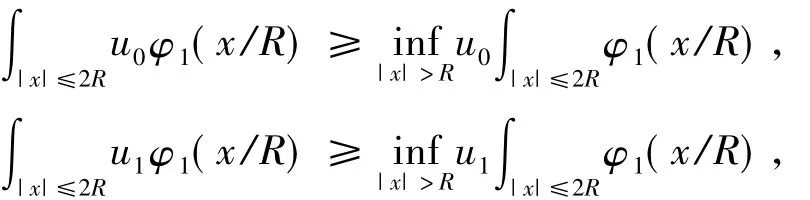
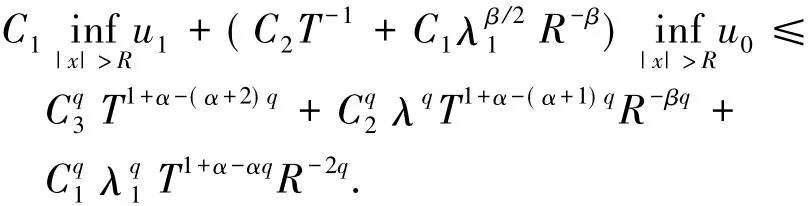
于是

让R→+∞，有极限

估计式( 25)和( 26)可推出下面的结果:

当T＜+∞时，假如lim+infu1= +∞或者lim+infu0|x|→∞|x|→∞=+∞，我们将得到矛盾．

4定理2的证明

从式( 24)得出

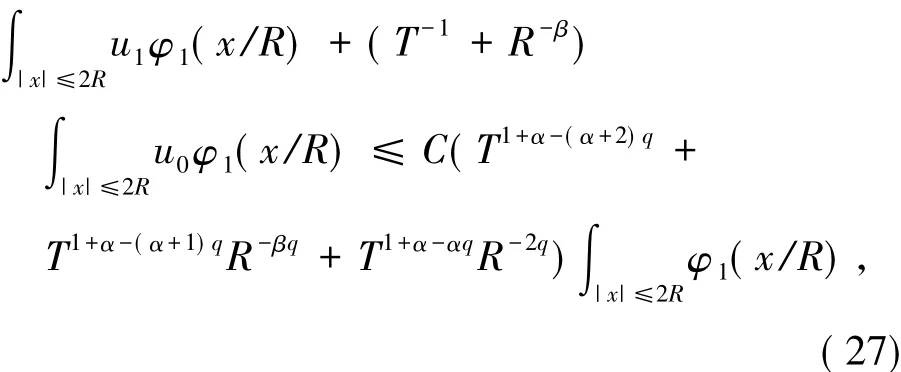
然后在式( 27)中取T=R，有

因而

因为1≤β≤2，有

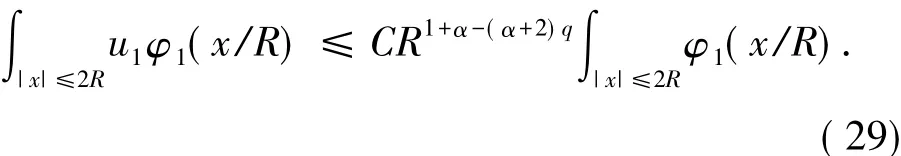
现在式( 29)的右边使用sup pφ1⊂{ x | R≤| x |≤2R}，有

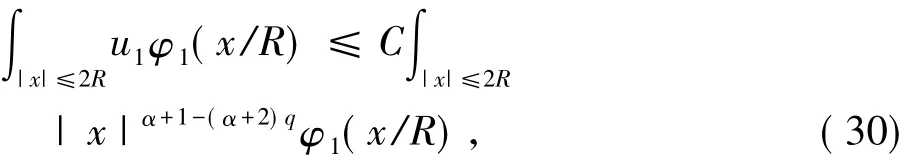
并且在式( 29)的左边再次使用sup pφ1⊂{ x| R≤| x| ≤2R}，有

联合式( 30)和( 31)可推出

最后我们在式( 32)的两边分别除以∫| x|≤2R| x |(α+2) q－(α+1)φ1( x/R)，得出

让R→+∞，有

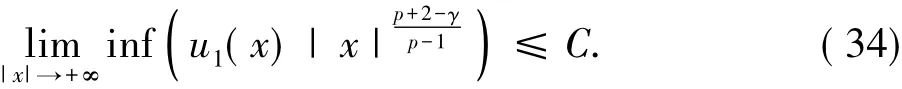
相似地，从式( 28)可得出

或者

与式( 34)的讨论相类似，有

或者

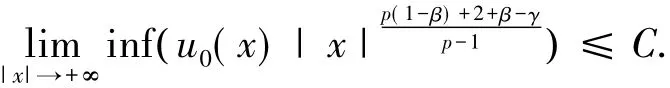
综上，完成了定理2的证明．

参考文献:

［1］DEBNATH L，BHATTA D．Integral tranforms and their applications［M］．Boca Raton，Fl: Chapman＆Hall/crc 2014: 31－37．

［2］CHEN W，HOLM S．Physical interpretation of fractional diffusion wave equation via lossy media obeying frequency power law［J］．Mathematical Physics，2003，0303040: 1－6．

［3］GREENBERG J M，MACCAMY R，MIZEL V J．On the existence，uniqueness，and stability of solutions of the equation ［J］．J Math Mech，1967/1968，17: 707－728．

［4］CARVALHO A N，CHOLEWA J W．Attractors for strongly damped wave equations with critical nonlinearities［J］．Pacific J Math，2002，207: 287－310．

［5］TODOROVA G，YORDANOV B．Critical exponent for a nonlinear wave equation with damping［J］．J Differential Equations，2001，174: 464－489．

［6］KIRANE M，LASKRI Y．Nonexistence of global solutions to a hyperbolic equation with a space－time fractional damping ［J］．Applied Mathematics and Computation，2005，167: 1304－1310．

［7］KIRANE M，QAFSAOUI M．Fujita' s exponent for a semilinear wave equation with linear damping［J］．Adv Nonlinear Stud，2002，2: 41－49．

［8］ZHANG Q S．A blow－up result for a nonlinear wave equation with damping: the critical case［J］．Acad Sci Paris，2001，333: 109－114．

［9］FINO A Z．Critical exponent for damped wave equations with nonlinear memory［J］．Nonlinear Analysis Theory Methods＆Application，2011，74( 16) : 5495－5505．

［10］BARAS P，KERSNER R．Local and global solvability of a class of semilinear parabolic equations［J］．J Differential E－quations，1987，68: 238－252．

［11］BARAS P，PIERRE M．Critère d'existence de solutions positives pours des equations semi－linéaires non monotones ［J］．Ann Inst H Poincaré－Anal Non Linéaire，1985，2: 185－212．

［12］SAMKO S G，KILBAS A A，MARICHEV O I．Fractional integrals and derivatives，theory and applications［M］．New York: Gordon and Beach Science Publishers，1987: 1－1016．

Nonexistence of Solutions to a Wave Equation with Fractional Integrals

XU Yongqiang1，2

( 1．School of Mathematics and Statistics，Minnan Normal University，Zhangzhou 363000，China; 2．School of Physics and Mechanical＆Electrical Engineering，Xiamen University，Xiamen 361005，China)

Abstract:In this paper，using a method based on a duality argument with an appropriate choice of the test function and a scaling argument，we establish some conditions that ensure the absence of global solutions to a wave equation with a nonlocal nonlinearity and obtain necessary conditions for the local and global solvability．

Key words:wave equations; nonlinearity; fractional integral; global nonexistence; weak solutions

基金项目:国家自然科学基金( 10976026)

收稿日期:2014－10－31录用日期: 2015－08－26

doi:10．6043/j．issn．0438－0479．2016．01．016

中图分类号:O 175．25

文献标志码:A

文章编号:0438－0479( 2016) 01－0086－05

Email: yqx458@ 163．com

引文格式:许勇强．带有分数积分的波动方程解的非存在性［J］．厦门大学学报(自然科学版)，2016，55( 1) : 86－90．

Citation: XU Y Q．Nonexistence of the solutions to a wave equation with fractional integral［J］．Journal of Xiamen University( Natural Science)，2016，55( 1) : 86－90．( in Chinese)