量子环面上导子李代数的一类不可约权模

徐诚慷，谭绍滨

(厦门大学数学科学学院，福建厦门361005)



量子环面上导子李代数的一类不可约权模

徐诚慷，谭绍滨*

(厦门大学数学科学学院，福建厦门361005)

摘要:量子环面是一类重要的非交换环面，它与高维仿射李代数的关系十分密切，它的导子李代数也在高维仿射李代数的表示理论里有着重要的作用．设D是一个有n+1个变量的量子环面，且其中有n个变量是相互交换的．本文对量子环面D的导子李代数给出了一类权模，证明这些模是权空间有限维的不可约模，并决定了它们的权的支集．

关键词:导子李代数;量子环面;高权型模;张量模

记A为d个变量的Laurent多项式环，Wd为A上的导子李代数．Shen［1］和Larsson［2］先后构造了一类权空间维数一致有界的Wd-模，称之为张量模．Rao［3］又证明了这些张量模囊括了所有满足一定条件的不可约WdA-模(交换李代数A自然地作用在张量模上)，并且猜测权空间有限维的不可约Wd-模只有两类:张量模和高权型模．其中高权型模在文献［4］中已有构造．值得注意的是A在高权型模上不是自然的作用，而且高权模的权空间也不一定是一致有界的［4］．最近Billig和Futorny［5］对权空间维数有限的不可约Wd-模给出了完全的分类，证实了Rao的猜想．

量子环面是Laurent多项式环的非交换推广．它和它的导子李代数在研究A型高维仿射李代数的结构理论中起着十分重要的作用．因此研究量子环面上的导子李代数的表示理论是十分有意义的．文献［6］中描述了d+1个变量的量子环面CQ上导子李代数D的结构．与李代数Wd类似，权空间有限维的不可约D-模应该至少包含张量模和高权型模这两类．在文献［7］中，作者推广Larsson的定义，得到了D的张量模，并证明了它们是完全可约的．文献［8］则详细地给出了这些张量模的不可约子模．最近在文献［9］中，作者在一定的限制条件下，分类了权空间维数有限的不可约DCQ-模，并证明了这类不可约模都是张量模．值得注意的是在张量模上有一个比较自然的CQ作用，而且权空间是一致有界的．虽然对导子李代数D的张量模已经有了丰富的结果，但是对其高权型模的研究还是空白．在本文中，我们对一类有理量子环面给定了其导子李代数D的一类高权型模;证明D的高权型模是不可约，且权空间维数是有限，但不是一致有界的;最后还计算了这类不可约模的权的支集．

我们分别用C，Z，Z+来记复数集、整数集和非负整数集，用U( g)记一个李代数g的泛包络代数．

1量子环面导子李代数及其高权型模

在这一节给出本文所研究的量子环面上的导子李代数及其高权型模的定义．取定正整数d和d个本原单位根q1，…，qd，令q=( q1，…，qd)．记J为非交换Laurent多项式环C［t0±1，t±11，…，t±d1］nc中由以下元素生成的理想，

记Cq∶= C［t0±1，t1±1，…，td±1］nc/J．它是一个有d个互相交换的变量的有理量子环面．

为叙述方便，约定以下记号:分别用m，n，r，s，…和u，v，w，…来表示Zd+1和Cd+1中的向量;而对Cd和Zd中的向量，则分别用u，v，w，…和m，n，r，s，…之类的记号表示．并对m∈Zd+1约定m= ( m0，m)，其中m0∈Z，m∈Zd．对m=( m0，m1，…，md)∈Zd+1，记tm= tm11…tmdd和tm=t0m0t1m1…tmdd= tm00tm．另外用(·|·)来表示向量空间Cd+1中通常的内积．定义

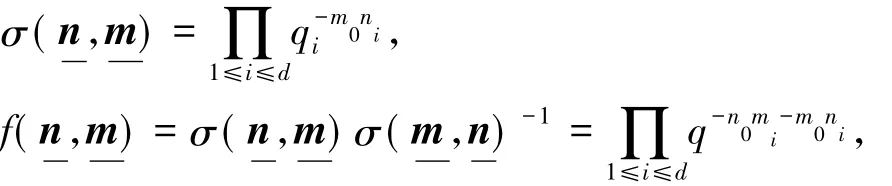
radf={n∈Zd+1|对任意的m∈Zd+1，f(n，m) = 1}．记D为Cq的导子李代数，结构［6］如下:

这里adtm是内导子，D0，D1，…，Dd为Cq的度导子，即

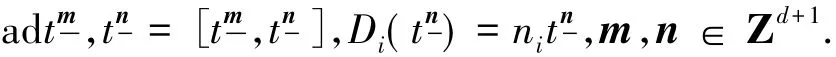
1)对m，nradf，

2)对mradf，n∈radf和u∈Cd+1，

3)对m，n∈radf，u，v∈C，

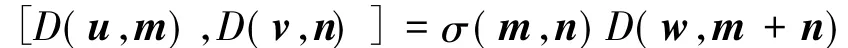
对任意的k∈Z，我们记D( k)=⊕D( k，m)，则D =m∈Zdk⊕∈ZD( k)是D的一个Z-阶化．由引理1和上述的李关系可知D0=spanC{ D0，D1，…，Dd}是D的一个极大交换子代数，而且D关于D0的根空间分解与引理1给出的D的Zd+1-阶化是一致的．对一个D(或D( 0)) -模M，如果D0在M上的作用半单，那么称M是一个权模．

记D±=⊕D( k)，那么D=D－⊕D( 0)⊕D+是D的一±k＞0个三角分解．假设V是一个D( 0)的权模，令D+在V上的作用平凡，由此将V看做一个( D( 0)⊕D+) -模．考虑诱导D-模M( V) =U( D)⊗U( D( 0)⊕D+)V．记M( V)rad为M ( V)中所有与V相交平凡的子模的和，那么在与V相交平凡的意义下，M( V)rad是M( V)唯一的极大子模．令L( V) = M( V) /M( V)rad，我们称L( V)为D的高权型模，那么显然地有如下的引理:

引理2如果D( 0)-模V是不可约的，那么D-模L ( V)也是不可约的．

下面给出一类具体的D( 0)-权模，它源于Shen与Larsson所定义的张量模．为此首先回顾张量模的定义［1－2］，然后再给出D( 0)在张量模上的作用．

令A = C［t1±1，…，td±1］⊂Cq，它是d个变量的Laurent多项式环．记Wd为A的导子李代数，那么

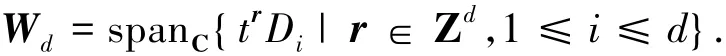
给定一个α∈Cd和一个gld-模V，在V⊗A上定义一个Wd的作用如下:对v∈V和s∈Zd，记v( s) = v⊗ts∈V⊗A．定义

其中u∈Cd，r，s∈Zd，v∈V，Eji是在( j，i)处元素为1，其他处元素为0的d×d阶矩阵．它定义了一个Wd-模Fα( V) = V⊗A，称为张量模．

记AWd=WdA，作为李代数，AWd的李乘积为

其中u，v∈Cd，r，s∈Zd，w=( u|s) v－( v|r) u．AWd有一个一维的中心Ct0和一个极大的交换子代数h=span { t0，D1，…，Dd}．对任一非零c∈C，定义［3］

这在V⊗A上定义了一个AWd的关于h的权模结构，记这个权模为Fα，c( V) = V⊗A．

接下来我们给出AWd的一个子代数，并证明它同构于李代数D( 0)．令

Wd( q) = spanC{ trDi| r∈Z( q)，1≤i≤d}．显然Z( q)是Zd的一个加法子群，且对任意r∈Zd，存在正整数p使得pr∈Z( q)．令AWd( q) = Wd( q)A．则它是AWd的一个子代数．注意到h⊂AWd( q)，因而Fα，c( V)自然是AWd( q)的关于h的权模．

命题1 D( 0)≌AWd( q)

证明直接验证可知如下定义的线性映射ρ: D( 0)→AWd( q)有:

是一个李代数同构．

由命题1，Fα，c( V)自然地成为了一个D( 0)-模．注意到上述同构将D0映到h，这就说明了Fα，c( V)是D( 0)的一个权模．由此我们得到一类D的高权型模

2主要结论及其证明

下面是本文的第一个主要结论:

定理1取定c≠0以及α∈Cd．如果V是一个不可约的有限维gld-模，那么高权型D-模Lα，c( V)是一个权空间维数有限的不可约模．

证明注意到D，D( 0)和Fα，c( V)分别是文献［10］所定义的Zd-额外阶化指数-多项式李代数，Zd-阶化指数-多项式李代数和具有有限指标集的Zd-阶化指数-多项式D( 0)-模，那么由文献［10］中的定理1．5可知Lα，c( V)是权空间有限维的．

下面证明Lα，c( V)是不可约D-模．由引理2和命题1，只需证明Fα，c( V)是不可约AWd( q) -模．

我们任取Fα，c( V)的非零AWd( q) -子模W．由于Fα，c( V)是权模，W包含非零的权向量v( m)，其中v∈V，m∈Zd．考虑环面A的作用，对任意的r∈Zd，有

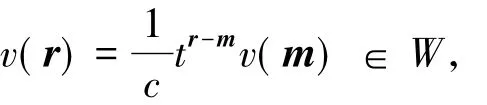
所以存在子空间V1⊆V使得W=V1⊗A．

取Cd的一组标准正交基{ e1，…，ed}．记pi为使得piei∈Z( q)的最小正整数，那么对任意的1≤i，j≤d，v ∈V1和m∈Zd有所以( Ejiv) ( m+pjej)∈W，那么Ejiv∈V1．因此V1是一个gld-模．由于V是不可约gld-模，有V1=V．所以W = Fα，c( V)．即Fα，c( V)是不可约AWd( q) -模．

对D0的权模M，称M所有的权构成的集合为M的权的支集．下面计算高权型模的权的支集．记

取定gld-模V的一组基{ va}a∈I，其中I是一个指标集．注意到作为D( 0)-模，Fα，c( V)的支集SuppFα，c( V) = ( c，α) +( { 0}×Zd)．由诱导模的构造和Poincaré－Birkhoff－Witt定理知，M( Fα，c( V) )的权的支集为

SuppM( Fα，c( V) ) = ( c，α) + Zd+1(≤)⊂Cd+1．由于Lα，c( V)是M( Fα，c( V) )的一个商模，所以它的支集SuppLα，c( V)是( c，α) +Zd+1(≤)的子集．记＞为Zd+1上的字典序，那么我们知道有自然的定义，而且M ( Fα，c( V) )有一组基

其中k，l∈Z+，m( 1)…m( k)∈Zd+1(＜) adf，n( 1)…n( l)∈Zd+1(＜)∩radf，0≤i1，…，il≤d，a∈I，s∈Zd．

定理2取定c≠0以及α∈Cd．如果V是一个不可约gld-模，那么D-模Lα，c( V)的权的支集为

证明先证包含关系⊇．由Fα，c( V)⊂Lα，c( V)，知道( c，α) +( { 0}×Zd)⊂SuppLα，c( V)．下面证明( c，α) +( { k∈Zq|k＜0}×Zd)⊂SuppLα，c( V)．

如果不然，我们知道即存在μ= ( c+m0，α+m)SuppLα，c( V)，其中m0∈Zq，m0＜0，m∈Zd．那么由权空间M( Fα，c( V) )μ中任一向量生成的D-模都是M( Fα，c( V) )的真子模．

由于V是非平凡的，则存在v∈V，1≤i，k≤d使得Ekiv≠0．那么有( tm00D0) v( m)∈M( Fα，c( V) )μ，且N= U( D) ( t0m0D0) v( m)M( Fα，c( V) )是一个真子模．由于m0∈Zq，则存在n∈Zd使得(－m0，n)∈radf．注意到对r∈radf，s∈Z( q)，我们有r+( 0，s)∈radf．通过加pkek∈Z( q)到n上，不妨假定n∈Zd满足如下条件(这个假定用到了Ekiv≠0) :

(－m0，n)∈radf，而且( ei|α+ m) v +

那么

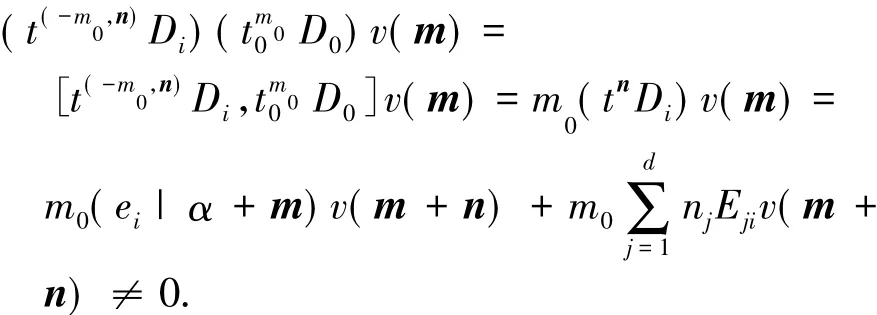
下面证明反包含关系“⊆”．记W为M( Fα，c( V) )由以下线性空间生成的D-子模:

l ∈Z，元素tm( 1)，…，tm( k)，tn( 1)，…，tn( l)，i1，…，il，a，s与式( 1)中所述一致，所以W⊆M( Fα，c( V) )rad．由D中的交换关系，可得W的另一组基

令γ=( c，α) +r，其中r∈Zd+1满足r0＜0，r0Zq．注意到对k个满足如下条件的正整数a1，…，ak:

至少存在一个aiZq．不妨假设a1，…，alZq，al+1，…，ak∈Zq，其中l≤k．由此可以看到M( Fα，c( V) )γ中的基向量

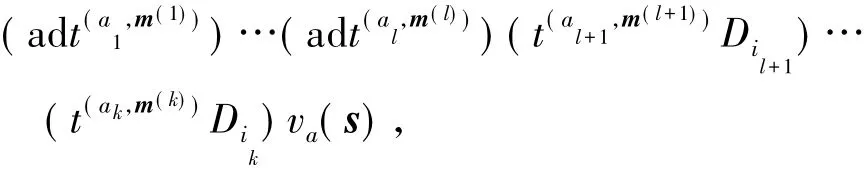
其中m( 1)，…，m( k)∈Zd，1≤il+1，…，ik≤d，a∈I，s∈Zd，与式( 2)中向量的形式一致．所以M( Fα，c( V) )γ⊂W⊆M( Fα，c( V) )rad，这就证明了γSuppLα，c( V)．因此包含关系“⊆”成立．

参考文献:

［1］SHEN G Y．Graded modules of graded Lie algebras of Cartan type I．Mixed products of modules［J］．Sci Sinica Ser A，1986，29: 570－581．

［2］LARSSON T A．Conformal fields: a class of representations of vect( N)［J］．Internat J Modern Phys A，1992，7 ( 26) : 6493－6508．

［3］ESWARA R S．Partial classification of modules for Lie－algebra of diffeomorphisms of d－dimensional torus［J］．J Math Phys，2004，45: 3322－3333．

［4］BERMAN S，BILLIG Y．Irreducible representations for toroidal Lie－algebras［J］．J Algebra，1999，221: 188－231．

［5］BILLIG Y，FUTORNY V．Classification of simple wn－modules with finite－dimensional weight space［EB/OL］．［2013－04－19］．http:∥arxiv．org/pdf/1304．5458．pdf．

［6］BERMAN S，GAO Y，KRYLYUK Y S．Quantum tori and the structure of elliptic quasi－simple Lie algebras［J］．J Funct A－nal，1996，135: 339－389．

［7］LIN W，TAN S．Representations of the Lie algebra of derivations for quantum torus［J］．J Algebra，2004，275: 250－274．

［8］LIU G，ZHAO K．Irreducible modules over the derivation algebras of rational quantum tori［J］．J Algebra，2011，340: 28－34．

［9］ESWARA RAO S，BATRA P，SHARMA S S．The irreducible modules for the derivations of the rational quantum torus［J］．J Algebra，2014，410: 333－342．

［10］BILLIG Y，ZHAO K．Weight modules over exp－polynomial Lie algebras［J］．J Pure Appl Algebra，2004，191: 23－42．

A Class of Weight Modules for the Derivation Lie Algebras of Quantum Tori

XU Chengkang，TAN Shaobin*

( School of Mathematical Sciences，Xiamen University，Xiamen 361005，China)

Abstract:Quantum torus is a very important class of non－commutative torus．Not only it has a close relation with the extended affine Lie algebra，but also its derivation Lie algebra plays a significant role in the representation theory of the extended affine Lie algebra．Let D be a quantum torus with n+1 variables with n of them commuting．In this paper，we study a class of weight modules for the derivation Lie algebra of the quantum torus D．We show that these modules are irreducible and occupy finite dimensional weight spaces．Furthermore，their supports are calculated explicitly．

Key words:derivation Lie algebra; quantum torus; module of highest weight type; tensor module

*通信作者:tans@ xmu．edu．cn

收稿日期:2014－12－29录用日期: 2015－06－25

doi:10．6043/j．issn．0438－0479．2016．01．014

中图分类号:O 152．5

文献标志码:A

文章编号:0438－0479( 2016) 01－0078－04

引文格式:徐诚慷，谭绍滨．量子环面上导子李代数的一类不可约权模［J］．厦门大学学报(自然科学版)，2016，55( 1) : 78－81．

Citation: XU C K，TAN S B．A class of weight modules for the derivation Lie algebras of quantum tori［J］．Journal of Xiamen University ( Natural Science)，2016，55( 1) : 78－81．( in Chinese)