基于EEMD的公路客流量波动性与周期性研究
2016-04-11秦喜文邢婷婷董小刚高中华刘媛媛
秦喜文,邢婷婷,董小刚,高中华,张 瑜,刘媛媛
(1.长春工业大学研究生院,吉林 长春 130012;
2.长春工业大学基础科学学院,吉林 长春 130012;
3.长春工业大学汽车工程研究院,吉林 长春 130012)
基于EEMD的公路客流量波动性与周期性研究
秦喜文1,2,3,邢婷婷2,董小刚2,高中华2,张瑜2,刘媛媛2
(1.长春工业大学研究生院,吉林 长春 130012;
2.长春工业大学基础科学学院,吉林 长春 130012;
3.长春工业大学汽车工程研究院,吉林 长春 130012)
[摘要]为实现对公路客流量进行快速且准确预测,提出了将公路客流短期预测的总体平均经验模态加以分解的EEMD方法.通过将原始时间序列分解为多个固有模态函数与趋势项之和,对多个固有模态函数进行周期性和波动性分析,揭示出各阶模态间的周期性变化规律以及不同时间段内的波动特点,进而证明了总体平均经验模态分解方法的合理性与有效性.
[关键词]总体平均经验模态分解;固有模态函数;波动性;周期性
随着我国经济的迅猛发展和城乡一体化建设的全面展开,公路客运因其安全、快捷、舒适、高效和高质量全程服务等优越性,日渐成为大众出行的一个重要选择.[1]因此,研究公路客流的客流量特点及发展趋势并讨论其周期性和波动性,对客运公司制定运营计划、提高客运服务质量、增强公路客运的市场竞争力等方面具有重要的现实指导作用.公路交通虽然具有载客量大、速度快、安全性高等优势,但同时也存在一定的不足,如运营环境的特殊、运营空间的有限和管理效能低等,这些都会导致客流量不稳定.本文根据短期公交客流量预测的非线性、非平稳性以及影响因素较多的特点,提出了一种基于EEMD的研究方法,并利用该方法对公路客流量的波动性和周期性进行分析.
1EEMD方法介绍
HHT方法是由N.E.Huang提出的一种适应性更广且能处理复杂非线性和非平稳信号的分析方法,即基于经验模态分解(EMD)的一种时频分析方法.此方法与Fourier分析相比,HHT方法可以处理非平稳和瞬态问题;与小波分析相比,吸收了小波变换多分辨的优势,却避免了基函数的选择问题.同时具备比现有所有信号处理方法更强的局部特性,因此成为一种先进有效的信号分析处理方法,其本质就是对信号进行平稳化处理.[2]然而EMD在处理信号的过程中,也存在着由于算法的局限和信号的间断等因素导致出现模态混叠现象,使得分析得到的效果并不理想,为解决这个问题,Huang等[3]提出了对EMD方法的改进,即结合噪声辅助分析方法的总体平均经验模态分解方法,简称EEMD方法.本研究主要基于EEMD方法对客流量其波动性和周期性特点进行分析.
HHT方法的核心是EMD分解,其过程是将任意复合信号分解成有限个固有模态函数(IMF)之和,关键是如何把一个非平稳序列分解为有限个IMF分量和一个趋势项,同时把本征模函数分量定义为在信号中加入了有限振幅的白噪声之后的多次集成的均值.本研究采用的是对EMD方法改进后的EEMD方法,即总体平均经验模态分解方法.总体来说就是在原信号中加入若干次均匀分布的高斯白噪声,目的是将分解的IMF丢失的尺度补全,再各自进行EMD处理,最后求平均的一种全局化方法.此方法将加入的白噪声互相抵消,使分解的结果不仅保留原序列的信号信息,而且很大程度上克服了模态混叠,使分解在物理上唯一.[3]
EEMD方法具体步骤如下:
(1)通过给待分析信号x(t)中加一组白噪声w(t),构成信噪混合体
X(t)=x(t)+w(t).
(2)对信噪混合体X(t)进行EMD分解,分解成各个IMF分量的组合

(3)给待分析信号中加入不同的白噪声wi(t),并重复以上两步:
Xi(t)=x(t)+wi(t);
分解后得到各自的IMF分量组

(4)对得到的IMF组合下相对应的IMF求均值
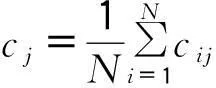
其中N表示整体的个数.从而最终的分解结果为

在待处理的信号上附加一个白噪声后将具有如下特征:
(1) 白噪声具有零均值特性,即附加噪声的次数足够多时,噪声就可以达到被消除的效果.
(2) 白噪声的加入和多次计算均值可以使得最终得到的结果与真实信号相当.
2实证分析
客流量是典型的非线性、非平稳的时间序列,针对这一情况我们处理数据的方法应与普通信号处理方法有所不同,本研究尝试将EEMD方法应用于短期客流量数据的处理和分析中.
2.1公路客流量的EEMD分解
本文的研究数据主要采用近10年的公路客流量数据,数据来源于长春市客运总站.该数据基本上反映了公路客流的变动情况.
通过对2003—2012年间的客流量数据进行EEMD分解和分析,发现第50个数据明显高于其他数据.根据长春市公路客流的原始数据和异常点的定义可知,可确定该点为异常点.一般而言,异常点的出现是由于系统受到外部或内部非正常的干扰所产生的,它会带来虚假的信息,但也提供关于系统稳定性、灵敏度等信息,因此我们不能忽视异常点.在处理数据时,应剔除高度异常的异常值,再利用现有变量的信息,对异常值(缺省值)进行填补.但当剔除异常值造成了数据的残缺时,就违背了时间序列“顺序的重要性”原则,从而导致结果的不准确.[4]为此,当序列中存在缺省值时,一般用插值法来补足缺省值,插值过程所遵循的原则是以达到最理想的插值效果为目的而进行方法的选择.本研究利用三次样条插值函数对数据进行插值,替换掉第50个异常值数据,经过预处理后的长春市公路客流量的时序图,如图1所示.
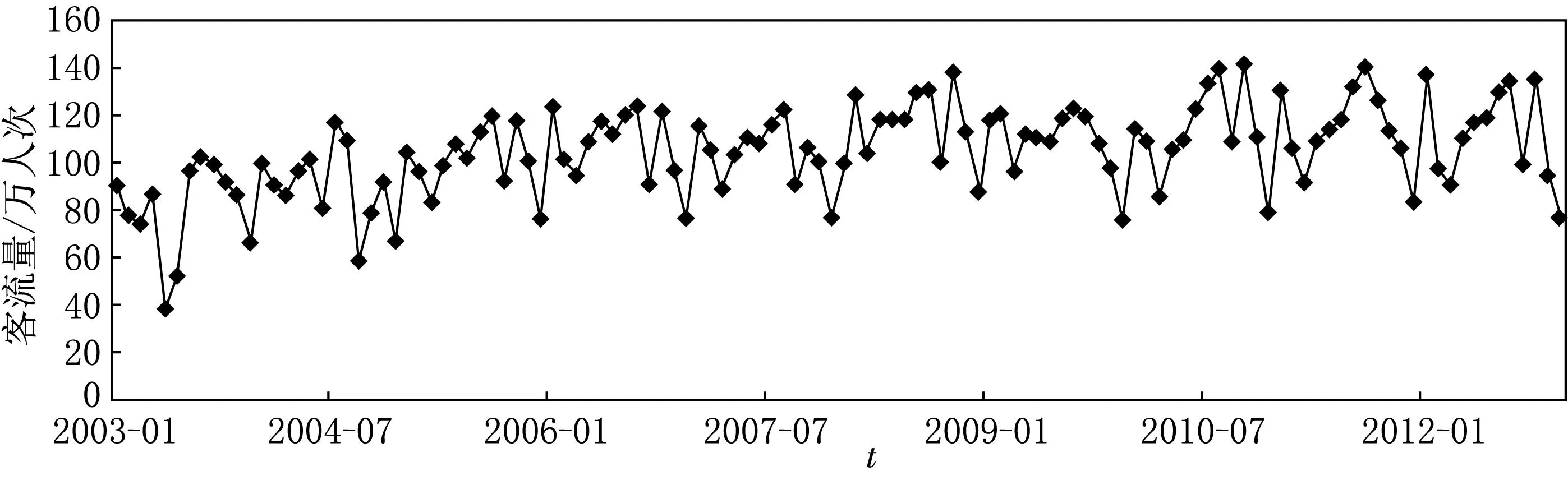
图1 长春市公路客流量时序图
对2003年1月至2012年12月公路月客流量,总计120个数据进行EEMD分解,共得到5阶固有模态函数和一个剩余的趋势项,如图2所示(图2中各图的纵坐标均表示客流量,单位为万人次).通过EEMD方法对公路客流量时间序列进行处理,将原始序列分解,得到若干个不同尺度的分量,对其进行研究可以准确地分析出公路客流量的波动性与周期性.[5]
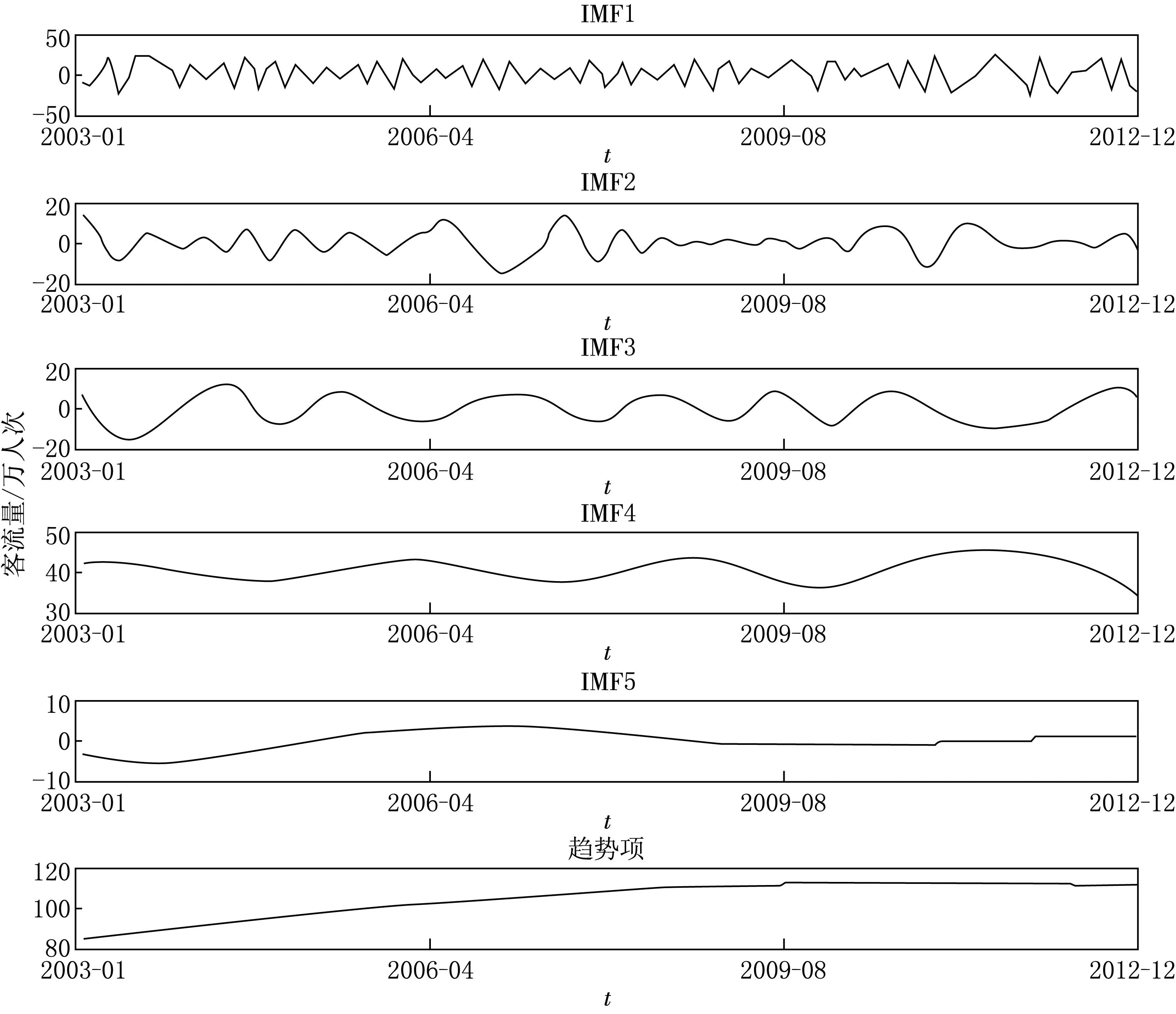
图2 固有模态函数(IMF)和趋势项(TREND)
从图2中可以看出分解后的各阶IMF频率由高到低依次排列,分解后的剩余趋势项是单调的.具体来讲:IMF1的高频振荡能够很好地刻画出客流量的波动细节,与原序列的波动趋势大体一致;IMF2和IMF3的振动频率依次降低,虽然在IMF2中反映出2006年末到2007年初有较大波动,但从IMF3中可以看出这一阶段客流量整体表现仍为上升趋势;IMF4和IMF5的振动频率显然低于图示的IMF1—IMF3,体现出波动尺度较大的特征,其在2008年末出现较大幅度波动;最后的剩余趋势项是一条基本呈上升趋势的曲线,它并不直观地反映客流量的波动情况,但它可以体现数据的整体水平.[6]
EEMD方法把公路客流量数据分解为不同尺度和频率的固有模态函数IMF,但考虑到在不同时间尺度上公路客流量的较大差异以及每个IMF在不同时期的波动对于总客流量的贡献不同,我们需要一个能够衡量各阶IMF相对于EEMD分解前总客流量所占波动比率的量,因此引进波动率的表述,本文将波动率定义为任意时刻IMF的绝对值与原始信号的比值,即


经过EEMD分解重构后的IMF1与IMF2的波动和波动率曲线如图3所示.从图3中我们可以看出,在2003年初到2012年末这10年间,有两个时间段的波动幅度比较大,分别为每年的11月到次年的2月和每年的6月到8月.引起较大波动的主要原因是我国春节假期与学生的寒暑假.这说明我们的计算结果与实际情况基本吻合.
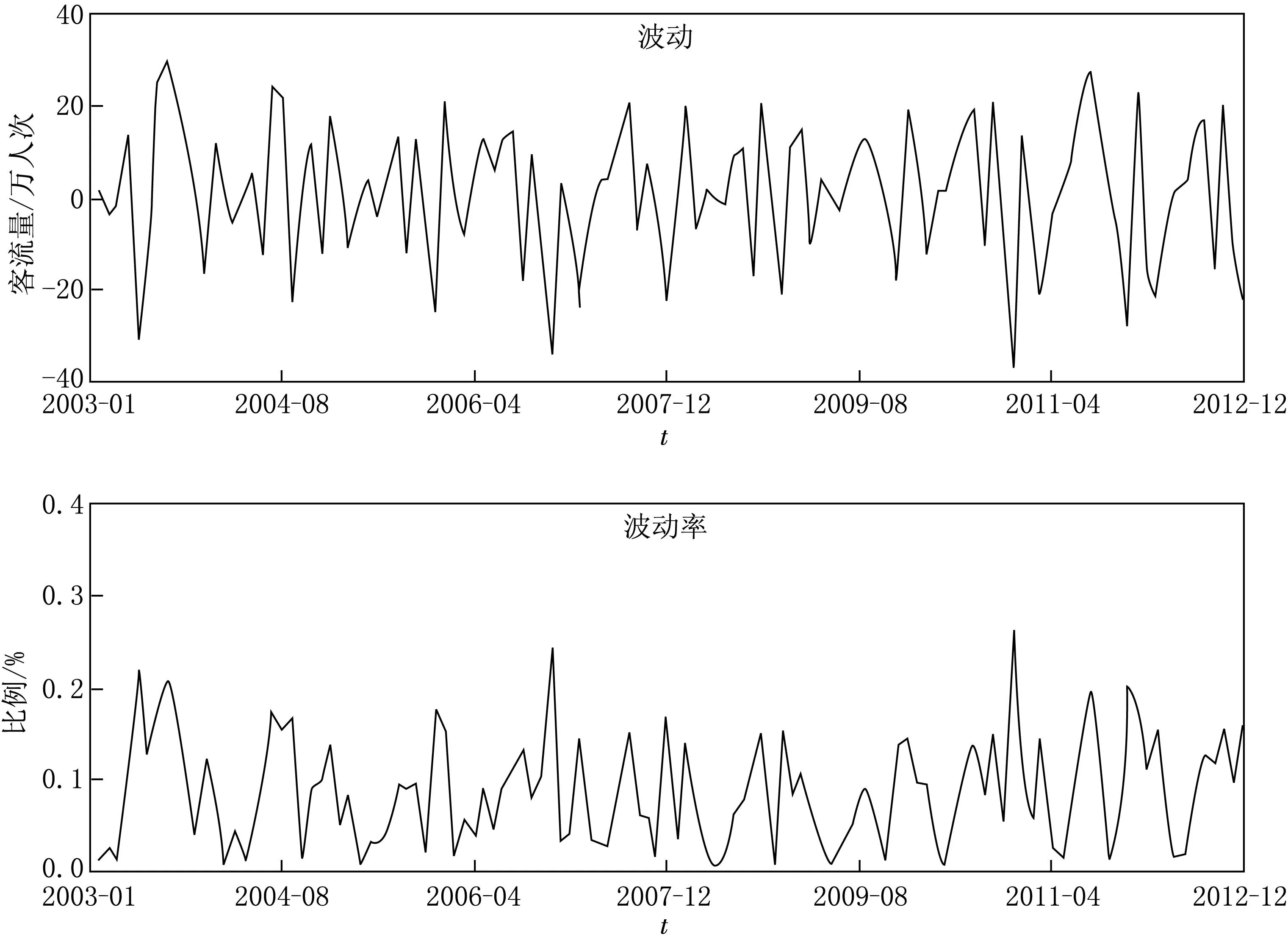
图3 IMF1和IMF2的波动和波动率曲线
2.2公路客流量的各阶IMF的周期性分析
这里采用平均周期法计算经EEMD分解后的各IMF周期,得到的各阶IMF振荡周期可以更直观地观察到客流量的周期性变化规律.平均周期法采用如下定义
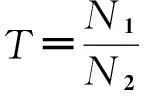
其中N1为公路客流量时间序列中的数据数目总量,N2为极小值点或极大值点的数目.即通过统计波峰和波谷的数量得到公路客流量的振荡周期,详见表1.从表1中我们不难发现各分量的平均振荡周期大致呈增长趋势,其中3.333,6.316和13.333分别为IMF1,IMF2,IMF3所得到的平均周期.由此可大致反映出在一个季度,半年和一年时间尺度上的波动趋势.[7]

表1 各阶IMF的周期
3总结
EEMD方法是基于信号局部特征,把复杂的信号函数加以分解的过程,是一种自适应的时频局部化分析方法.本文将EEMD方法应用在具有非线性、非平稳性特征的公路客流量分析中,将客流量数据分解为有限个固有模态函数和一个趋势项.通过对分解后的各阶IMF进行波动性与周期性分析,运用波动率来衡量各阶IMF不同时期的波动对于总客流量的影响,运用各阶IMF的周期计算出平均周期.这体现了EEMD方法可以有效地提取原始时间序列中不同周期的分量,揭示各模态在不同时间尺度上的周期规律.
[参考文献]
[1]杨柳靑.基于EEMD的航空客流需求预测技术及其应用研究[D].武汉:华中科技大学,2009:15-21.
[2]HUANG N E,SHEN Z,LONG S R,et al. The empirical mode decomposition method and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc R Soc Lond A,1998,454:903-995.
[3]WU Z,HUANG N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis,2009,1(1):1-41.
[4]许廷霆,李克平.应用EMD方法分析交通流量的动态特性[J].科学技术与工程,2009,9(11):25-32.
[5]HUANG N E,SHEN S P. The Hilbert-Huang transform and its applications[M]. Singapore:World Scientific Publishing Company,2005:289-302.
[6]蔡赟姝,卢志明.基于经验模态分解的上证综合指数时间序列分析[J].上海大学学报(自然科学版),2012,18(4):3-6.
[7]赵泓扬,刘立生,韩庆邦.一种基于HHT和神经网络的智能轴承状态监控系统[J]. 东北师大学报(自然科学版),2013,45(2):73-78.
(责任编辑:李亚军)
The volatility and periodicity of highway passenger volume based on ensemble empirical mode decomposition
QIN Xi-wen1,2,3,XING Ting-ting2,DONG Xiao-gang2,GAO Zhong-hua2,ZHANG Yu2,LIU Yuan-yuan2
(1.Graduate School,Changchun University of Technology,Changchun 130012,China;2.School of Basic Sciences,Changchun University of Technology,Changchun 130012,China;3.Automotive Engineering Research Institute,Changchun University of Technology,Changchun 130012,China)
Abstract:In order to achieve the forecasting of the highway passenger volume quickly and accurately, the volatility and periodicity of the highway passenger volume is studied based on ensemble empirical mode decomposition(EEMD) method, which is very important for establishing and optimizing the passenger highway operation plan. The original time series is decomposed into a series of intrinsic mode functions (IMF) and a trend item. By analyzing the volatility and periodicity of each function,the different volatility features of the highway passenger volume with different scales are shown, which implies the volatility characteristics of the passenger volume in different period and the periodic property in different IMF. Consequently,it can be proved that the rationality of the EEMD method is feasible and effective.
Keywords:ensemble empirical mode decomposition;intrinsic mode functions (IMF);volatility;periodicity
[中图分类号]O 29[学科代码]110·71
[文献标志码]A
[作者简介]秦喜文(1979—),男,博士,副教授,主要从事HHT理论与应用研究;通讯作者:董小刚(1961—),男,教授,博士生导师,主要从事应用统计研究.
[基金项目]国家自然科学基金资助项目(11301036,11226335);吉林省教育厅科研项目(2014第127号,2013第142号).
[收稿日期]2014-05-21
[文章编号]1000-1832(2016)01-0044-05
[DOI]10.16163/j.cnki.22-1123/n.2016.01.011
