基于非线性规模经济效应的轴辐式网络枢纽选址研究

胡志华，王雅琪

(1.上海海事大学物流研究中心，上海 201306；

2.同济大学经济与管理学院，上海 200331)



基于非线性规模经济效应的轴辐式网络枢纽选址研究

胡志华1，2，王雅琪1

(1.上海海事大学物流研究中心，上海 201306；

2.同济大学经济与管理学院，上海 200331)

[摘要]在轴辐式网络单分配模型的基础上，改变传统将规模经济效应处理为折扣系数常量的方法，建立了基于可变规模经济效应的非线性规划模型.将以流量为自变量的枢纽间非线性转运成本函数进行分段线性化，从而将其转化为混合整数线性规划模型，应用Gurobi进行求解.通过算例讨论了单调可变的规模经济效应对枢纽点选择的影响，研究了在p-Hub问题中p的变化对枢纽网络的影响.结果表明，建立的模型能够拓展于处理任意非线性规模效应关系.

[关键词]轴辐式网络；规模经济效应；枢纽选址问题；干线运输

0引言

轴辐式网络是指OD (Origin to Destination)流一般先从起始点汇集于一个枢纽，然后转运到另一个枢纽，再配送到终点.轴辐式网络能够充分发挥物流网络货物运输的规模经济效应，优化物流成本.对于枢纽之间的干线运输，货物集中后运量大，通过优化运输工具和运输方式以提高运输满载率，从而使得枢纽之间的干线运输具有规模经济效应，使单位运输成本降低.人们对轴辐式网络进行了大量的研究，考虑到干线运输的规模经济效应，Abdinnour-Helm引入运输折扣系数，即在枢纽点之间的干线运输上定义运输折扣系数α(0≤α≤1)，表示在枢纽间干线货流所产生的规模效益相对于辐节点与枢纽之间运输成本的折扣，以此揭示干线规模经济效应对轴辐式网络模型的影响.[1-18]

在规模经济效应可变的条件下，对以总成本最低为目标的轴幅式网络枢纽选址的问题进行了研究.将目标函数中的转运成本剥离出来，将其转换为关于可变折扣系数的非线性函数，并进一步通过分段线性化使之转化为分段线性函数进行计算.在引入折扣系数的基础上，通过考虑非线性的可变规模经济效应反映轴辐式网络干线规模运输问题，研究非线性规模效应对轴辐式网络设计的影响，为轴辐式网络设计提供参考.

1分段线性化模型

在轴辐式网络单分配模型[M1]的基础上，建立了基于可变规模经济效应的非线性规划模型[M2].在模型[M2]中，将枢纽间非线性转运成本函数进行分段线性化，从而将非线性规划模型转化为混合整数线性规划模型，再进行求解.

图1　一个单变量函数的分段线性近似

(1)

(2)

求出.采用斜率(F(Xi+1)-F(Xi))/(Xi+1-Xi)描述时，得到

(3)

(4)

αi≤hi-1+hi，∀i=1，…，n；

(5)

(6)

(7)

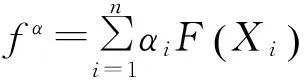
(8)

(4)—(8)式可以简化特殊有序集约束.定义一组变量成为特殊有序集k(SOSk)，有序集的元素取非零值，但必须是相邻的.大多数混合整数线性规划(MILP)求解器能够自动处理类型1和2的特殊有序集.本文将折扣系数α定义为SOS2变量，利用此方法将非线性的转运成本函数转化为线性成本函数.

2问题定义

2.1问题描述与假设

本文考虑了单分配轴辐式网络枢纽选址及非枢纽分配问题.单分配轴辐式网络要求每条OD流必须经过1个或2个枢纽点，进而使枢纽之间货物流量增加，这是规模经济效应的基础.在研究轴辐式网络时，通常会假设干线运输具有规模经济效应.能否取得规模经济效应以及能够取得多少规模经济效应是轴辐式网络设计的重点，如果建成网络后，发现规模经济效应较低，势必会造成浪费.本文考虑的规模经济效应体现在干线运输的折扣系数上，随着干线货流的变化，规模经济效应发生变化，因此折扣系数也发生变化.为了研究规模经济效应的变化对轴幅式网络枢纽选址的影响，通过设置规模效应函数的离散断点，引入SOS2变量，将由折扣系数变化造成的非线性函数转化为线性函数.在此基础上研究可变规模经济效应对轴幅式网络的影响，为了凸显运量对折扣系数的影响，不考虑运输距离对折扣系数的影响.首先，考虑固定折扣系数，建立轴辐式网络枢纽选择的基本模型.然后，将折扣系数设定为关于货流的函数，此时轴辐式网络枢纽间干线运输的规模经济效应为运量的非线性函数，对基本模型进行扩展.将基本模型与扩展模型进行对比，分析对最优枢纽个数popt等的影响.将p值由n变为n+1时枢纽点集合中新加入(相互替换)的节点定义为枢纽选入点Hp(p=n+1).通过求解p值下的模型，得到一个枢纽选入序列，通过枢纽选入序列的变化，说明某一或同一节点在不同的规模经济衡量模式下呈现的成本节约贡献程度.

2.2符号定义

相关参数和变量定义如下：

(1) 集合与索引

(b) S={1，…，LS}为间断点集合，即S索引.

(2) 参数

(a) Fk为在k点建立枢纽的固定成本；

(b) Dij为从节点i到j的距离，且认为距离满足三角不等式；

(c) χ为单位距离内单位流量的收集成本；

(d) δ为单位距离内单位流量的配送成本；

(e) Wij为从节点i到j的流量；

(h)Xs为间断点s的横坐标；

(3) 决策变量

(a)yikl为从节点i出发，经过枢纽k和l的流量；

(c)ykl为经过枢纽k和l的流量；

3模型

在以下模型中，αkls是SOS2变量，其向量分量中至多有2个分量不为零，且必须相邻.

3.1基本模型

在基本模型[M1]中，总成本分为4部分：建设成本，枢纽点的设施建设及设备购买等成本；收集成本，由非枢纽点运往枢纽点的货物流量所产生的物流成本；配送成本，由枢纽点运往非枢纽点的货物流量所产生的物流成本；枢纽点间的转运成本，在枢纽点间进行的货物运输所产生的物流成本.

[M1]Minimizef1=fsetup+fcol+fdist+fhh；

(9)

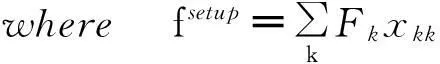
(10)

(11)

(12)

(13)

s.t.

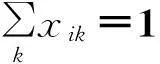
(14)

xik≤xkk，∀i，k∈N；

(15)

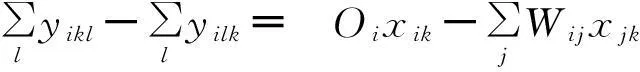
(16)

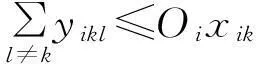
(17)

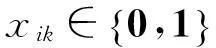
(18)

yikl≥0，∀i，k，l∈N.

(19)

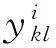
3.2扩展模型

在[M1]的基础上，考虑表示干线运输成本折扣系数的非线性函数的线性化，得到[M2].

(20)

where约束((10)—(12))

(21)

s.t.

约束((14)—(19))

(22)

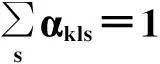
(23)

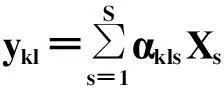
(24)

(25)

其中：目标函数(20)式包括[M1]的约束(10)—(12)，即建设成本、收集成本和配送成本，而在[M1]中的枢纽间的转运成本则修订为关于α的非线性函数；(21)式体现运输规模经济效应；新约束(22)式是干线流量约束等式；(23)式表示SOS2变量的和为1；(24)式表示干线运量可由给定间断点横坐标以SOS2的组合形式表示；(25)式表示干线单位距离运价可由给定间断点纵坐标以SOS2的组合形式表示.从而通过分段线性处理把非线性的转运成本函数转化为线性函数.

4实验部分

4.1算例

下面算例是应用p-hub问题CAB数据集[19].CAB数据集包括25个节点，记为N={1，2，…，25}.设置p的初值为3.通过改变p值，可以确定最优枢纽数popt.

已知节点之间的货流量Wij、距离Dij(i，j∈N)，假定Dij=Dji，利用Gurobi(www.gurobi.com)求解模型.设非枢纽点与枢纽间的单位距离单位运量的运输成本为1，即收集与分配成本均为1.而枢纽的固定成本采用表1设置.

表1　节点的枢纽建设成本　万元

4.2实验步骤与实验结果

具体的实验步骤和模型调整与分析见表2，相应的结果见表3—7以及图2.

表2　实验步骤

表3　规模经济效应不变时(p=3，[M1])和变化时(p=3，[M2])枢纽选址与非枢纽分配

表4　规模经济效应不变时([M1])和变化时([M2])各项成本　万元

表5　规模经济效应不同时的各项成本对比　万元

表6　枢纽点数目不同时的各项成本　万元

表7　[M1]与[M2]选取枢纽点比较

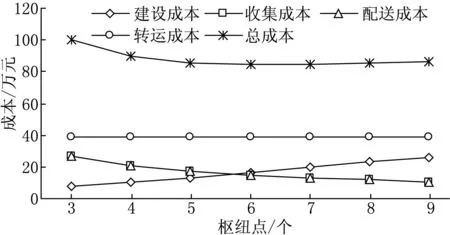
图2　不同枢纽点数目下的各项成本

从表7可以看出，采用固定的规模经济效应常数和采用非线性的规模经济效应的枢纽序列有一定差别.因此，当按照基本模型采用固定折扣系数来设计轴辐式网络是不合理的.

综合上述实验及其分析结果可知：在枢纽点数目相同时，枢纽点选择以及非枢纽点对枢纽的分配关系也存在差异；增加枢纽点数目会增加建设成本、收集成本，而配送成本会减少，转运成本无明显变化.

5结论

轴辐式网络干线运输规模经济效应的实现可以降低网络成本.本文将干线运输规模效应的折扣系数作为一个变量来考虑.随着货流量的增加，通过改变运输工具或运输方式以提高满载率，规模经济效应将发生明显变化.考虑可变的规模经济效应使得转运成本变为流量的非线性函数，从而建立轴辐式网络设计的非线性混合整数规划模型.本文通过分段线性近似法对非线性函数设置分段点，将非线性函数转化为线性函数.通过对模型求解结果比较发现，非线性规模效应会影响枢纽点的选择.在实际情况中，运价依赖于货流量，货流量越大运价越低，规模经济效应越显著.在这种情况下，采用固定折扣系数，不能反映运量对成本的动态影响.因此，基于非线性规模经济效应的轴辐式网络模型能够更好地反映货流量规模对成本的影响.

[参考文献]

[1]ABDINNOUR-HELM S. A hybrid heuristic for the uncapacitated hub location problem[J]. European Journal of Operational Research，1998，106(2/3)：489-499.

[2]O’KELLY M E. The Location of Interacting hub Facilities[J]. Transportation Science，1986，20(2)：92-106.

[3]JEONG S J，LEE C G，BOOKBINDERC J H. The European freight railway system as a hub-and-spoke network[J]. Transportation Research Part A，2007，41(6)：523-536.

[4]HORNER M W，O’KELLY M E. Embedding economies of scale concepts for hub network design[J]. Journal of Transport Geography，2001，9(4)：255-265.

[5]ABDINNOUR-HELM S，VENKATARAMANAN M A. Solution approaches to hub location problems[J]. Annals of Operations Research，1998，78(1)：31-50.

[6]ALUMUR S A，NICKEL S，SALDANHA-DA-GAMA F. Hub location under uncertainty[J]. Transportation Research Part B Methodological，2012，46(4)：529-543.

[7]O’KELLY M E，BRYAN D L. Hub location with flow economies of scale[J]. Transportation Research Part B Methodological，1998，32(8)：605-616.

[8]O’KELLY M，SKORIN-KAPOV D，SKORIN-KAPOV J. Lower bounds for the hub location problem[J]. Management Science，1995，41(4)：713-721.

[9]CAMPBELL J F，STIEHR G，ERNST A T，et al. Solving hub arc location problems on a cluster of workstations[J]. Parallel Computing，2003，29(5)：555-574.

[10]EBERY J，KRISHNAMOORTHY M，ERNST A，et al. The capacitated multiple allocation hub location problem formulations and algorithms[J]. European Journal of Operational Research，2000，120(3)：614-631.

[11]KRATICA J，STANIMIROVIC Z，TOSIC D，et al. Two genetic algorithms for solving the uncapacitated single allocationp-hub median problem[J]. European Journal of Operational Research，2007，182(1)：15-28.

[12]PAMUK F S，SEPIL C. A solution to the hub center problem via a single-relocation algorithm with tabu search[J]. IIE Transactions (Institute of Industrial Engineers)，2001，33(5)：399-411.

[13]SUNG C S，JIN H W. Dual-based approach for a hub network design problem under non-restrictive policy[J]. European Journal of Operational Research，2001，132(1)：88-105.

[14]CAMPBELL A M，LOWE T J，ZHANG L. Thep-hub center allocation problem[J]. European Journal of Operational Research，2007，176(2)：819-835.

[16]张世翔，霍佳震. 基于轴辐式网络模型的长三角地区城市群物流配送体系规划研究[J]. 管理学报，2005，2(2)：194-199.

[17]翁克瑞. 带固定轴线成本的轴辐式网络设计问题[J]. 运筹学学报，2012，16(1)：88-96.

[18]倪玲霖，史峰. 多分配快递轴辐网络的枢纽选址与分配优化方法[J]. 系统工程理论与实践，2012，32(2)：441-448.

[19]O’KELLY M E. A quadratic integer program for the location of interacting hub facilities[J]. European Journal of Operational Research，1987，32(3)：393-404.

(责任编辑：石绍庆)

Hub location problem of hub-and-spoke network with non-linear effects of economies of scale

HU Zhi-hua1，2，WANG Ya-qi1

(1.Logistics Research Center，Shanghai Maritime University，Shanghai 201306，China；2.School of Economics and Management，Tongji University，Shanghai 200331，China)

Abstract:So based on a single allocation model of hub-and-spoke network whose effects of economies of scale are treated by constant discount factors，a nonlinear programming model is devised to present the nonlinear effects of economies of scale by the transported volume. The approach based on piecewise linearization on the nonlinear cost function of transported volumes among hub-hub trunks is applied. Therefore，the nonlinear programming model is transferred into a mixed-integer linear programming model，which can be solved by Gurobi. Compared to the method that uses constant discount factors to calculate the hub-hub transportation cost，the proposed model considers variable effects of economies of scale presents practical relations between the transportation costs and transported volumes. By the linearization method，this model can be effectively solved. In the experimental study，the paper analyzed the influences made by variable monotonous effects of economies of scale on hub selection and the influence of the selection of p in p-Hub problems on the design of hub network. The established model can be expanded to deal with any nonlinear effects of economies of scale.

Keywords:hub-and-spoke network；economies of scale；hub location problem；trunk transportation

[中图分类号]U 491.1[学科代码]580·2099

[文献标志码]A

[作者简介]胡志华(1977—)，男，博士，副教授；主要从事港航与物流运作优化、社会科学计算实验、计算智能研究.

[基金项目]国家自然科学基金资助项目(71101088，71171129，71390521)；上海市曙光计划项目(13SG48)；教育部博士点基金资助项目(20113121120002，20123121110004)；上海市科委项目(11510501900，12510501600，12ZR1412800)；教育部人文社会科学研究项目(09YJA630072).

[收稿日期]2014-10-16

[文章编号]1000-1832(2016)01-0090-07

[DOI]10.16163/j.cnki.22-1123/n.2016.01.019