地铁隧道断面变形分析方法研究

刘冠兰，徐亚明，柏文峰

(1. 武汉大学测绘学院，湖北 武汉 430079； 2. 精密工程与工业测量国家测绘地理信息局

重点实验室，湖北 武汉 430079； 3. 广州地铁设计研究院有限公司，广东 广州 510010)



地铁隧道断面变形分析方法研究

刘冠兰1，2，徐亚明1，2，柏文峰3

(1. 武汉大学测绘学院，湖北 武汉 430079； 2. 精密工程与工业测量国家测绘地理信息局

重点实验室，湖北 武汉 430079； 3. 广州地铁设计研究院有限公司，广东 广州 510010)

A Method to Determine the Deformation of Tunnel Section

LIU Guanlan，XU Yaming，BAI Wenfeng

摘要：针对目前以单点描述隧道断面变形的不足，本文采用B样条曲线拟合隧道断面扫描数据，计算待分析部位两期曲线段的豪斯多夫距离，以各部位曲线段的整体变形信息来反映断面变形。同时根据地铁隧道断面扫描数据的特点，提出了B样条曲线拟合的主点选取方法以及非断面信息的剔除方法。最后以某地铁隧道断面扫描数据为例，通过加入模拟变形信息拟合分析，验证了该方法的有效性。

关键词：隧道变形监测；B样条曲线拟合；豪斯多夫距离

传统的地铁隧道结构变形监测主要是在隧道断面上布设监测点，通过单点的变形值来反映隧道断面变形[1-3]，但单点并不能准确地反映隧道断面。采用测量机器人或扫描仪采集相对密集的隧道断面数据，拟合断面曲线进行分析比较，可有效掌握断面的整体变形信息。文献[4—5]利用三维点云数据拟合椭圆形断面进行收敛变形分析，但在长期不均匀荷载影响下的隧道断面并不是标准的圆(椭圆)，采用椭圆拟合会平滑掉断面的局部变形信息。样条曲线是用来描述自由曲线的常用手段，对于局部偏转角度小于π/6的点集，可以采用三次样条曲线来拟合插值[6]。其中B样条曲线具有局部支承性质，能够描述隧道断面变形的局部特性。因此对于设计为光滑曲线(马蹄形、圆形)的隧道断面，可采用B样条曲线来拟合隧道断面并进行断面变形分析。

一、B样条曲线拟合

B样条曲线的参数方程定义为[5]

(1)

鉴于隧道断面扫描数据点是有序的，本章内容仅限于有序数据点的拟合问题。B样条曲线拟合包括3个步骤：参数化、节点矢量的确定以及最优化拟合。数据点的参数化方法很多，本文采用累积弦长参数化法[7]。

1. 确定节点矢量

Park给出了基于主点的节点矢量确定方法[8]：假设在给定点集pi(i=1,2，…,m)中确定了主点domj(j=1,2，…，n)，其中n≤m，节点矢量的计算公式为

(2)

本文根据隧道断面数据的特点，对主点选取方法进行了改进。对于较为光滑的隧道断面，曲率变化相对均匀，局部最大曲率点除包含曲线形状信息外还有部分噪声的存在。为尽量减小噪声的影响，在选取主点的时候以曲率和弧长两个指标作为依据，保证节点分布在顾及曲线形状信息的同时又相对均匀。节点矢量确定的具体过程为：

1) 计算离散点曲率值。通过连续的3个点Pi-1、Pi、Pi+1的曲线在Pi点处的离散曲率为Ki。Ki可由圆曲率来表达[9]

(3)

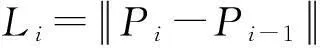
3) 计算节点矢量。采用式(2)计算节点矢量。

4) 曲线拟合，重新确定节点矢量。根据给定已知点集P的参数集T、节点矢量序列U，通过线性最小二乘求解各控制点，以得到初始曲线信息。由于离散点计算的曲率受噪声影响较大，在得到初始曲线后重新计算各点曲率信息，重复步骤2)—3)确定节点矢量。当给定曲线C(t)后，pi点曲率的计算公式为

(4)

2. 最优化曲线拟合

(5)

式中，tk为点pk到曲线上的最近点参数；d为点到曲线距离；ρ为tk处的曲率半径；Nk、Tk分别为tk处的单位法向量和单位切向量。

本文采用的最优化线性拟合的主要步骤为：

1) 确定初始B样条曲线。采用已知点集P的参数化结果以及节点矢量作为已知值，线性最小二乘求解的控制点，以此作为初始B样条曲线。

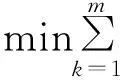
二、非断面信息的剔除和断面变形分析

1. 非断面信息的剔除

隧道断面总体为较光滑的曲线，但是由于光缆、管道等附件遮挡，扫描数据不可避免地存在非断面信息。这些错误信息的存在会影响曲线拟合的精度，同时会影响变形量的计算。本文利用曲率及点间距信息作为非断面信息的判定标准，采取迭代运算对其进行剔除。具体方法步骤如下：

1) 逐点计算离散点曲率值Ki、曲率变化值ΔKi=Ki-0.5×(Ki-1+Ki+1)以及各点与前、后扫描点的间距，将曲率值、曲率变化值的绝对值或间距值大于给定阈值的点作为初判非断面点，并予以剔除，存入非断面信息。

2) 对剩余点进行孤立点探测，剔除孤立点，并存入非断面信息。

3) 采用曲线拟合方法对剩余点进行曲线拟合。

4) 计算初判的非断面点至拟合曲线的最近距离，将小于给定阈值的点重新加入到曲线拟合点集中。

5) 重复步骤3)—4)，直至拟合点集中没有新增点。

2. 断面变形分析

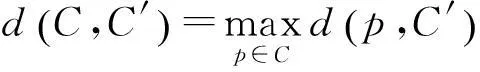
通常情况下这个距离并不是对称的，也就是说d(C,C′)≠d(C′,C)。因此两条曲线C和C′之间的豪斯多夫距离定义为

(6)

可以采用两期拟合曲线的豪斯多夫距离来进行断面曲线的变形分析。

三、应用实例

以徕卡TCRP1201自动全站仪无合作目标模式扫描采集的某地铁隧道断面数据为例，采用前述B样条曲线拟合方法进行断面曲线拟合。通过加入两组模拟变形数据的拟合结果与原始拟合结果计算豪斯多夫距离来验证本文方法的可行性及有效性。

1. 隧道断面的B样条曲线拟合

图1、图2为扫描数据以及扫描断面的实景图，可以看出原始扫描数据在断面信息中夹杂着很多其他附件的信息。

图1　某隧道断面扫描数据

图2　隧道断面实景

图3、图4分别为第一次和最终对断面扫描数据进行非断面信息分离的结果，图中实心点为断面信息，十字点为分离出来的非断面信息。试验选取的曲率绝对值阈值为2，曲率变化值阈值为4，点间距阈值取扫描间距的3倍，点至曲线的最近距离阈值取3倍的曲线拟合中误差和1 cm中较大的值。从图3中可以看到，由于离散点的局部曲率受邻近点的影响，一些非断面信息附近的断面点被误判为非断面点，图4显示这些误判点在迭代过程中被修正。考虑到扫描数据较为密集，非断面点的漏判比断面信息的误判对拟合结果的影响更大，同时断面信息的误判可在随后的迭代过程中获得修正，因此在基于曲率以及点间距信息的非断面数据判断中可设定较为严格的阈值。

图3　第一次分离结果

图4　最终分离结果

对已剔除非断面信息的断面扫描数据采用前述方法进行三次B样条曲线拟合。曲线拟合结果如图5所示，曲线上圈形点为断面拟合点，曲线外的星号点为所求的控制点。图6为拟合残差直方图，3组统计数据依次为拟合点到曲线的最近距离及其在X、Y方向上分量在指定范围内的点数，曲线拟合中误差为1.6 mm。

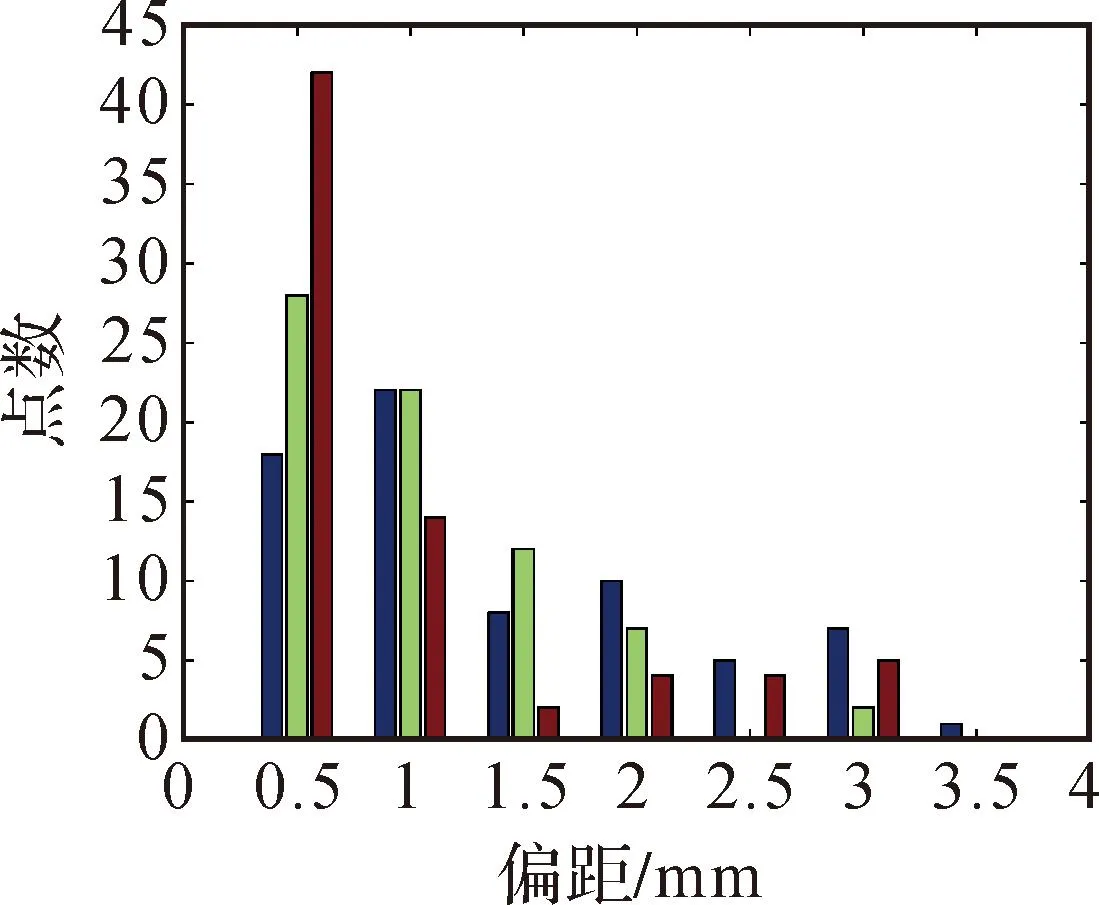
图6　曲线拟合残差直方图

2. 断面曲线的变形分析

根据全站仪的观测精度，扫描数据的点位精度为1.5 mm左右。试验1随机生成一组X、Y方向方差均为1 mm的零均值噪声加入扫描数据。加入随机噪声的扫描数据与原始数据可视为断面变形为0的两期扫描数据，分别计算其断面曲线C1、C2。选取如图7所示的断面左上和右下两个曲线段为例，计算两组数据拟合曲线的豪斯多夫距离。

图7　变形分析曲线段示意图

待分析曲线段的具体选取方式为：选定曲线C1上参数区间，计算曲线段两端点至曲线C2的最近距离点，由此得到C2上的参数区间。离散化两个曲线段以计算两个曲线点集之间的豪斯多夫距离。图8、图9分别为两段曲线d(p,C2)的统计直方图，统计量为距离落在上一横坐标与所在横坐标值之间的点数。最后得到的左上曲线段的豪斯多夫距离为1.4 mm，右下曲线段的豪斯多夫距离为1.6 mm。对于点位精度和拟合精度为1.5 mm左右的情况，该计算结果可认为断面无变形，基本与实际吻合。

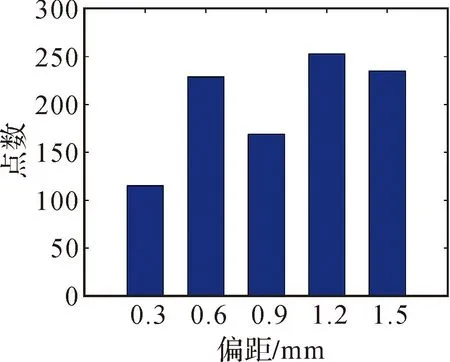
图8　试验1左上曲线段d(p,C2)统计直方图

图9　试验1右下曲段d(p,C2)统计直方图

为进一步分析B样条曲线拟合的断面变形，试验2在断面左下方扫描数据(前40个扫描点)X方向加入方差为1 mm,均值为3 mm的噪声，Y方向和其他部位扫描数据的X、Y方向加入方差为1 mm的零均值噪声进行拟合，并计算与原始数据拟合曲线的豪斯多夫距离。分析曲线段仍选取如图7所示两处。计算得到左上曲线段的豪斯多夫距离为1.5 mm，右下曲线段为3.3 mm。

分别统计右下曲线段的d(p,C2)在X、Y方向的分量，结果为X方向的豪斯多夫距离3.2 mm，Y方向-1.7 mm，计算结果与实际数据吻合。基于本试验算例可得出如下结论，对于隧道断面扫描数据可采用两期拟合曲线的豪斯多夫距离判断断面曲线的变形，变形方向由豪斯多夫距离的符号确定。

四、结束语

针对地铁隧道断面变形的需求，结合隧道断面扫描数据的特点，本文提出了：①适用于隧道断面数据的主点选取方法；②有效的非断面数据剔除方法；③基于B样条曲线拟合隧道断面数据，并利用豪斯多夫距离进行隧道断面变形分析的方法。最后以某隧道实际扫描数据为例，通过加入模拟变形数据对断面进行拟合和变形分析。试验表明，加入零均值噪声的模拟数据拟合的断面曲线与原始断面拟合曲线的豪斯多夫距离在1.5 mm左右，在数据精度为1.5 mm的情况下可认为断面未发生变形。在局部X方向加入均值为3 mm的噪声，模拟数据拟合的断面曲线与原始断面拟合曲线的豪斯多夫距离在远离变形区域为1.5 mm，局部变形区域为3.3 mm。计算结果与模拟变形吻合，由此验证了本文方法的可行性及有效性。

参考文献：

[1]卫建东.基于测量机器人的自动变形监测系统[J].测绘通报,2006(12):41-44,72.

[2]梅文胜,陈雪丰，周小波，等.盾构下穿既有隧道实时监测及其风险控制研究[J].武汉大学学报(信息科学版),2011,36(8):923-927.

[3]陈荣彬,林泽耿,李刚.测量机器人在地铁隧道监测中的研究和应用[J].测绘通报,2012(6):61-63.

[4]托雷,康志忠，等.利用三维点云数据的地铁隧道断面连续截取方法研究[J].武汉大学学报(信息科学版),2013,38(2):171-185.

[5]李珵,卢小平,朱宁宁，等.基于激光点云的隧道断面连续提取与形变分析方法[J].测绘学报,2015,44(9):1056-1062.

[6]SU B Q, LIU D Y. Computational Geometry—Curve and Surface Modeling[M]. Boston: Academic Press， 1989.

[7]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京：高等教育出版社，2001.

[8]PARK H， LEE J H. B-spline Curve Fitting Based on Adaptive Curve Refinement Using Dominant Points [J]. Computer-Aided Design, 2007, 39(6): 439-451.

[9]LIU G H, WONG Y S. Adaptive Fairing of Digitized Point Data with Discrete Curvature [J]. Computer-Aided Design, 2002(34):309-320.

[10]WANG W, POTTMANN H, LIU Y. Fitting B-spline Curves to Point Clouds by Curvature-based Squared Distance Minimization [J]. ACM Transactions on Graphics, 2006, 25(2): 214-238.

[11]LOURAKIS M I A. A Brief Description of the Levenberg-Marquardt Algorithm Implemented by Levmar[R].[S.l.]: Institute of Computer Science, Foundation for Research and Technology-Hellas, 2005.

[12]ASPERT N, SANTA-CRUZ D, EBRAHIMI T. Measuring Errors between Surfaces Using the Hausdorff Distance[C]∥Proceeding of the IEEE International Conference on Multimedia and Expo (ICME). [S.l.]: IEEE, 2002.

中图分类号：P258

文献标识码：B

文章编号：0494-0911(2016)02-0103-04

作者简介：刘冠兰(1984—)，女，博士，讲师，主要研究方向精密工程测量、工业测量。E-mail: glliu@sgg.whu.edu.cn

基金项目：湖北省自然科学基金(2015CFB501)；中央高校基本科研业务费专项资金青年教师资助项目(2042015k0058)

收稿日期：2015-03-27； 修回日期： 2015-10-31

引文格式： 刘冠兰，徐亚明，柏文峰. 地铁隧道断面变形分析方法研究[J].测绘通报，2016(2)：103-106.DOI:10.13474/j.cnki.11-2246.2016.0061.