计及转角影响的八轴独立电驱车稳定性控制*

高 玉，申焱华，刘相新，韦学中

(1.北京科技大学机械工程学院,北京 100083； 2.中国运载火箭技术研究院航天发射技术研究所,北京 100076)

2016065

计及转角影响的八轴独立电驱车稳定性控制*

高 玉1，申焱华1，刘相新2，韦学中2

(1.北京科技大学机械工程学院,北京 100083； 2.中国运载火箭技术研究院航天发射技术研究所,北京 100076)

针对后轴参与转向的多轴车辆高速行驶稳定性差的问题，本文中对某八轴电驱动车辆的稳定性控制开展研究。首先设计了基于多参数变权重和最优控制算法的横摆力矩控制器，提出了一种基于规则的横摆力矩分配策略和一种基于车辆行驶安全的驱动力调整策略，并考虑了转向时转角变化对驱动力分配的影响；接着建立八轴车2自由度控制系统模型和整车3维动力学模型，设计用于计算补偿横摆力矩的上层控制器和用于各轮驱动力分配的下层控制器；最后对驾驶员闭环系统的双移线路径跟踪进行仿真。结果表明，所建立的车辆稳定性控制器有效地提高了多轴车辆高速行驶稳定性。

多轴车；电驱动；稳定性控制；横摆力矩； 驱动力

前言

后轴参与转向的多轴车辆高速行驶稳定性差、转向时容易发生失稳现象。采用各轮独立电驱动形式，通过准确控制各轮驱动力形成附加横摆力矩来纠正车辆姿态，可改善多轴车辆高速行驶稳定性。

多电机独立驱动车辆的稳定性控制主要是横摆力矩估计和各轮驱动力分配的过程，各种文献研究的区别在于控制变量和采用控制算法的不同。控制变量主要为质心侧偏角、横摆角速度，控制算法有线性二次型最优控制算法[1-5]、滑模变结构控制理论[6]、神经网络自适应控制[7]和模糊控制[8]等。上述研究没有考虑质心侧偏角和横摆角速度两个控制变量之间的耦合关系，驱动力的分配只考虑单轨模型，没有考虑转向时转角变化对驱动力分配的影响。

本文中以某八轴电驱动车辆为模型，基于质心侧偏角和横摆角速度之间的耦合关系，设计最优直接横摆力矩(direct yaw-moment control，DYC)的上层控制器；在下层控制器的设计时，充分考虑转角变化的影响，并按照基于规则和车辆行驶安全的分配策略对横摆力矩进行分配。

1 多轴车模型

仿真模型主要包括整车动力学模型、电机模型和2自由度参考模型。

为能更准确地验证控制算法的有效性，八轴车的整车动力学模型应尽量与实际物理模型相接近。而悬架系统的非线性特性、主销侧倾和轮胎与路面间的瞬时特性很难用数学模型准确表述，为此在Adams/view环境中建立38个自由度的整车机械系统动力学模型，整车模型包括簧上质量的6个自由度，16个悬架的自由度和16个车轮的自由度，采用UA轮胎模型。

该八轴电驱动车辆配备16个轮边电机，通过轮边减速器降速增矩而驱动各车轮。图1为轮边电机的性能曲线。

图1 轮边电机模型

基于八轴车的基本结构和特性，建立八轴车的2自由度模型，如图2所示，前三轴与后两轴为转向轴，转向方式为逆相位转向。

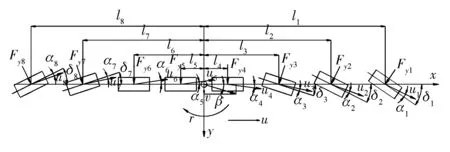
图2 八轴车2自由度模型

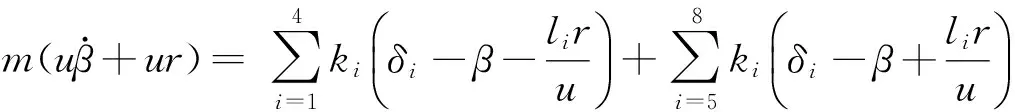
(1)

(2)式中:m为整车质量；li为第i轴到质心的距离；δi为各轴转角；ki为等效轮胎侧偏刚度，总定义为正值；i=1,2,…,8;Iz为汽车绕垂直轴的转动惯量；u为纵向速度；v为侧向速度；r为横摆角速度；β为质心侧偏角。

各轴相对一轴转角输入为

式中：i=2,3,7,8；Li5为第i轴到第5轴的距离，其中，L15，L25和L35为正，L75和L85为负。

2 控制器的设计

该多轴车的稳定性控制系统结构示意图如图3所示。整车控制器由上层横摆力矩控制器和下层驱动力分配控制器组成。

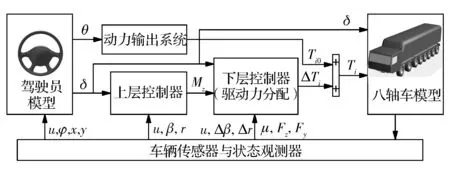
图3 八轴车稳定性控制系统结构示意图

2.1 上层控制器设计

上层控制器的结构原理图如图4所示。以驾驶员给定的转向盘转角δ、车速u、车辆的质心侧偏角β和横摆角速度r作为输入，经过相应的控制算法得到横摆力矩MZ，输出至下层控制器。上层控制器由前馈控制器、理想模型和反馈控制器组成，其中Mff为前馈补偿横摆力矩，rd和βd分别为理想横摆角速度和质心侧偏角，Mfb为反馈控制力矩。

2.1.1 控制系统模型

若给车辆一个附加的横摆力矩来控制车辆的操纵稳定性，则式(2)的右边加上横摆控制力矩MZ后与式(1)简化并写为状态方程的形式，则为

即

(3)

其中：

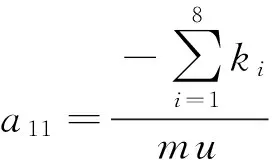
h1=0；h2=1/Iz；X=[βr]T；δf=δ1

质心侧偏角和横摆角速度的传递函数为

(4)

(5)

2.1.2 前馈控制器

前馈控制器的设计应考虑车辆的实际特性，为此研究了八轴车的转向特性。图5为八轴车辆的稳态横摆角速度和稳态质心侧偏角增益曲线，从稳态横摆角速度增益曲线来看，该八轴车辆的横摆角速度增益比中性转向时大，车辆表现为过多转向；质心侧偏角增益也随着车速的增加而加大。因此，车辆的稳态质心侧偏角和横摆角速度都须要进行控制。

图5 八轴车辆的稳态增益曲线

设计前馈补偿控制器，使车辆的稳态质心侧偏角和横摆角速度趋于理想值，补偿横摆力矩Mff与前轮转角的关系为

Mff(s)=Gffδf(s)

(6)

式中：Gff为前馈控制器的比例增益系数，由质心侧偏角和横摆角速度确定的初始系数按照变权重比例求和得到，其值的确定步骤如下。

(1) 基于质心侧偏角的前馈控制系数

令MZ(s)=Mff(s)，并结合式(4)和式(6)，可得到稳态转向时，补偿横摆力矩Mff作用下的质心侧偏角对前轮转角的响应为

(7)

理想的质心侧偏角大小可简化为

(8)

由式(7)和式(8)可得

(9)

(2) 基于横摆角速度的前馈控制系数

令MZ(s)=Mff(s)，并结合式(5)和式(6)，可得到稳态转向时，补偿横摆力矩Mff作用下的横摆角速度对前轮转角的响应为

(10)

理想的横摆角速度可简化为

(11)

将式(11)代入式(10)可得

(12)

不同车速下以质心侧偏角确定的前馈控制系数Gff1和以横摆角速度确定的前馈控制系数Gff2取值如图6所示。显然对车辆的质心侧偏角和横摆角速度进行控制所需的横摆力矩不同，当对二者进行单独控制时，必然会引起另一个参数的变化，即表现为二者之间的耦合作用，二者的误差不可能同时消除，因此必须确定合适的前馈控制系数，尽量降低二者的控制误差。

图6 不同控制变量下的前馈增益系数变化曲线

为此，设计不同权值变量的前馈控制器比例增益系数：

Gff=aGff1+(1-a)Gff2

(13)

式中a为Gff1的权重系数。

a的取值方法为：由图6可知，在车速低于33km/h之前，Gff1与Gff2对应的横摆力矩的调整方向相反，为保证车辆低速行驶时轨迹的准确跟随，应尽量使车辆接近中性转向，此时应主要以Gff2调整为主；车速大于33km/h之后，Gff1与Gff2的调整方向相同，若只通过Gff2进行调整，此时车辆的稳态横摆增益特性为中性转向，而此时车速较高，为避免车辆在高速行驶时转向盘过于灵敏，应在高速时使车辆具有适当不足转向特性，此时可适当增加Gff1的权重系数。同时考虑图5中多轴车辆的稳态质心侧偏角增益曲线接近于二次函数，因此定义a为车速的二次函数，即a=cu2，车速为100km/h时，取a=0.2，由此可求出常数c的取值。

2.1.3 车辆理想模型

将前馈控制力矩作用下的整车2自由度模型作为车辆的理想模型，则横摆角速度和质心侧偏角的理想传递函数分别为

(14)

(15)

因而理想模型的状态方程可写为

(16)

其中:

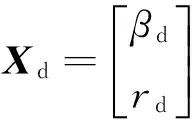
前馈控制后理想的稳态增益曲线如图7所示。对比图5可见，从稳态横摆角速度增益看，车辆的转向特性由过度转向变为不足转向，最高车速时的稳态质心侧偏角增益也由2.7降为1.5。

图7 八轴车的理想稳态增益曲线

2.1.4 反馈控制器

为使实际车辆的瞬态输出跟踪理想模型，降低外界干扰，应用线性二次型算法设计最优横摆力矩反馈控制器[3,9]。对反馈控制器中实际值与理想值的偏差求导：

(17)

将式(3)和式(16)代入式(17)，可得

(18)

令前轮转角引起的干扰项为零，则式(18)可进一步简化为

(19)

设反馈控制力矩为

Mfb=-Gfbe=-[gfb1gfb2]e

(20)

式中：gfb1和gfb2为实际车辆模型与理想模型的状态偏差反馈增益。

设最小化性能指标函数为

(21)

式中Q和R为常值矩阵，可借助Matlab求解Riccati方程得到反馈控制器增益值。

因此，总的附加横摆力矩为

MZ=Mff+Mfb

(22)

2.2 下层控制器设计

上层控制器计算得到附加横摆力矩MZ后，由下层控制器负责各轮驱动力的分配，驱动力分配原理如图8所示。根据车辆行驶状态和发生失稳的程度，分别建立基于规则的横摆力矩分配策略和基于车辆行驶安全的驱动力调整策略。

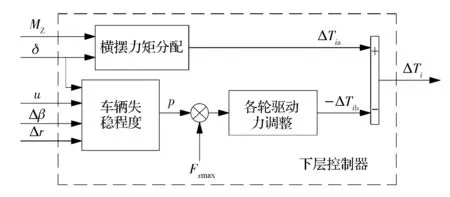
图8 下层控制器驱动力分配原理图

2.2.1 转向时的横摆力矩分配原则

车辆在小转向角度发生失稳时，横摆力矩的控制中仅对左右两侧车轮进行区分即可。但在较大转角情况下，转向轮绕质心形成横摆力矩的力臂改变，使得横摆力矩的大小和方向均可能发生改变，以整车右转为例。

图9为该车处于最大转角时的示意图。转向轮的力臂长度发生改变，且1，2和8轴内侧车轮的力臂越过质心点使该轮的横摆力矩方向改变，此时在横摆力矩的分配时，这3个车轮的驱动力调整方向应与外侧车轮一致，从而保证用最小的驱动力调整量形成最大的横摆力矩。因此，在各轮驱动力的调整时，必须考虑转向对各轮力臂大小和驱动力调整方向的影响。

2.2.2 基于规则的横摆力矩分配

定义横摆力矩MZ沿顺时针旋转方向时为正，即前轮右转为正，通过各轮驱动力调整量形成的横摆力矩为

(23)

式中：ΔFLia和ΔFRia为左右侧车轮的驱动力调整量，驱动力增加为正，驱动力降低为负；lLi和lRi为左右侧车轮驱动力在整车质心处形成的力臂，当第i轴车轮的力臂与同侧车轮力臂不相同时为负，相同时为正。

(24)

式中：mi和ni分别为左右两侧车轮的力臂系数，当第i轴车轮的力臂与同侧车轮力臂不相同时取1，相同时取2；ΔFLia0和ΔFRia0为各轮驱动力调整量的绝对值。

各轮驱动力形成横摆力矩的力臂长度lLi和lRi可以由内侧前轮转角和车辆几何尺寸参数确定。

当内侧前轮转角δ1不为0时，i轴内、外两侧轮转角为

(25)

式中i分别取1，2，3，7和8。

i轴内、外两侧车轮力臂分别为

(26)

式中B为轮距。

因此，左右两侧车轮的力臂为

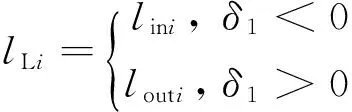
(27)

由横摆力矩确定的各轮驱动力调整量的绝对值ΔFLia0和ΔFRia0按照各轮垂向力的比值分配：

(28)

ΔFa0为横摆力矩分配时的各轮驱动力调整量的公约数值，可通过将式(24)～式(28)依次代入式(23)中求解得出。

2.2.3 基于车辆行驶安全的驱动力调整

对于后轴参与转向的多轴车辆，在高速转向失稳时，为保证车辆的行驶安全，在横摆力矩控制的同时，应减小各轮驱动力，使车速迅速降低，各轮驱动力的降低量ΔFib所形成的附加横摆力矩应始终为零：

(29)

(30)

其中：

ΔFb=pFxmax

(31)

(32)

式中：ΔFLib和ΔFRib为左右两侧车轮驱动力的降低量；ΔFb为驱动力的总降低量；Fxmax为路面所能提供的最大附着力；p为根据车辆失稳程度定义的车辆失稳系数；μs为路面附着系数；Fyi为轮胎的侧向力。

车辆失稳程度可通过质心侧偏角误差和横摆角速度误差评定，但车速越高车辆越容易发生失稳，因此文中的车辆失稳系数p由车速、质心侧偏角误差和横摆角速度误差3个参数决定。 设由3个参数确定的失稳系数分量分别为p1，p2，p3，当p2和p3为零时，无论p1多大，此时失稳系数p为零。因此可通过三者相乘得到车辆的失稳系数，即

p=p1·p2·p3

(33)

通常在车速低于40km/h时车辆发生失稳的可能较小，之后车速越高越容易失稳，因此定义p1与车速的3次方成正比：

p1=c1u3

(34)

最高车速时取p1=1，由此可求出常数c1的值。

当车辆的质心侧偏角误差和横摆角速度误差较小时，可认为没有发生失稳；误差超过一定限度后，则认为车辆发生严重失稳；在两者之间时，随着误差的增大失稳程度加重。为此将p2和p3表示为关于质心侧偏角误差和横摆角速度误差的非对称型Sigmoid函数：

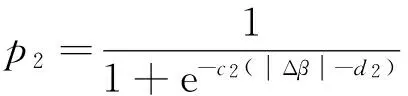
(35)

式中：|Δβ|和|Δr|为质心侧偏角误差和横摆角速度误差；c2，c3，d2和d3为相关的系数。

根据车轮转角的大小判断转向轮的力臂是否越过质心点(如2.2.1节所述)，将力臂越过质心点的j个内侧车轮按照外侧车轮处理，各轮驱动力调整量按照各轮垂向力的比值分配。则8-j个内侧车轮和其余8+j个外侧车轮中各轮驱动力调整量的表达式为

(36)

式中：FZin和FZout分别为8-j个内侧车轮和8+j个外侧车轮的垂向力之和；ΔFinb0和ΔFoutb0分别为内侧车轮和外侧车轮的需要调整的驱动力总量。

因此，根据ΔFb确定的驱动力降低量为

(37)

因此，下层横摆力矩分配后的各轮驱动力的调整量为

ΔFLi=ΔFLia-ΔFLib；ΔFRi=ΔFRia-ΔFRib

(38)

各轮要输出的总驱动力为

FLxi=FLxi0+ΔFLi；FRxi=FRxi0+ΔFRi

(39)

式中FLxi0和FRxi0为横摆稳定性调整之前的各轮初始分配驱动力。

各轮输出的驱动力还受电机输出能力的限制，因此，各轮实际输出的驱动力矩为

Txi=(min)·rr

(40)

式中：Fxi为横摆力矩分配之后各轮要输出的驱动力；Flim为电机所能输出提供给车轮的最大驱动力；rr为车轮的滚动半径。

3 控制策略验证与分析

为验证本文中所设计的横摆力矩控制器和驱动力分配算法的有效性，通过对驾驶员闭环路径跟踪控制[10]进行了基于Adams/view与Matlab/simulink软件的联合仿真。

在附着系数为0.4的水平路面上，驾驶员通过控制加速踏板开度，在最短的时间内加速至80km/h，之后保持加速踏板开度不变，在15s之后驾驶员控制转向盘使车辆跟踪设定的双移线车道行驶，仿真结果如图10～图14所示。图中对比了采用横摆力矩控制的电驱动车辆(电驱动DYC)与没有控制的机械传动方案(机械差速)的结果。

图10和图11分别为路径跟踪控制所对应的转向轮转角输入和车速。图12为闭环控制仿真的横摆角速度和质心侧偏角的误差。由图可见，与没有控制的机械差速方案相比，采用横摆力矩控制后，跟踪双移线路径时的最大横摆角速度误差和质心侧偏角误差分别降低了32%和22%以上。图13为闭环控制仿真的横摆力矩和各轮驱动力矩。由图可知，实际输出的横摆力矩并没有达到控制器给定的目标值，在最大横摆力矩处，实际的输出值只有目标值的30%左右，这是因为车轮的最大驱动力矩受电机实际输出能力的限制而使整车的驱动力降低，这也是图11中车速降低的原因。图14为闭环控制仿真的行驶轨迹。从最终控制效果看，没有控制时车辆的实际行驶路径与参考路径有很大的偏差，并且处于S型路线行驶，这对后轴参与转向的多轴车辆来说非常危险。而通过对电驱动车辆进行横摆力矩控制后，车辆能够较为准确地跟踪路径行驶，在很大程度上提高了多轴车辆的行驶安全。

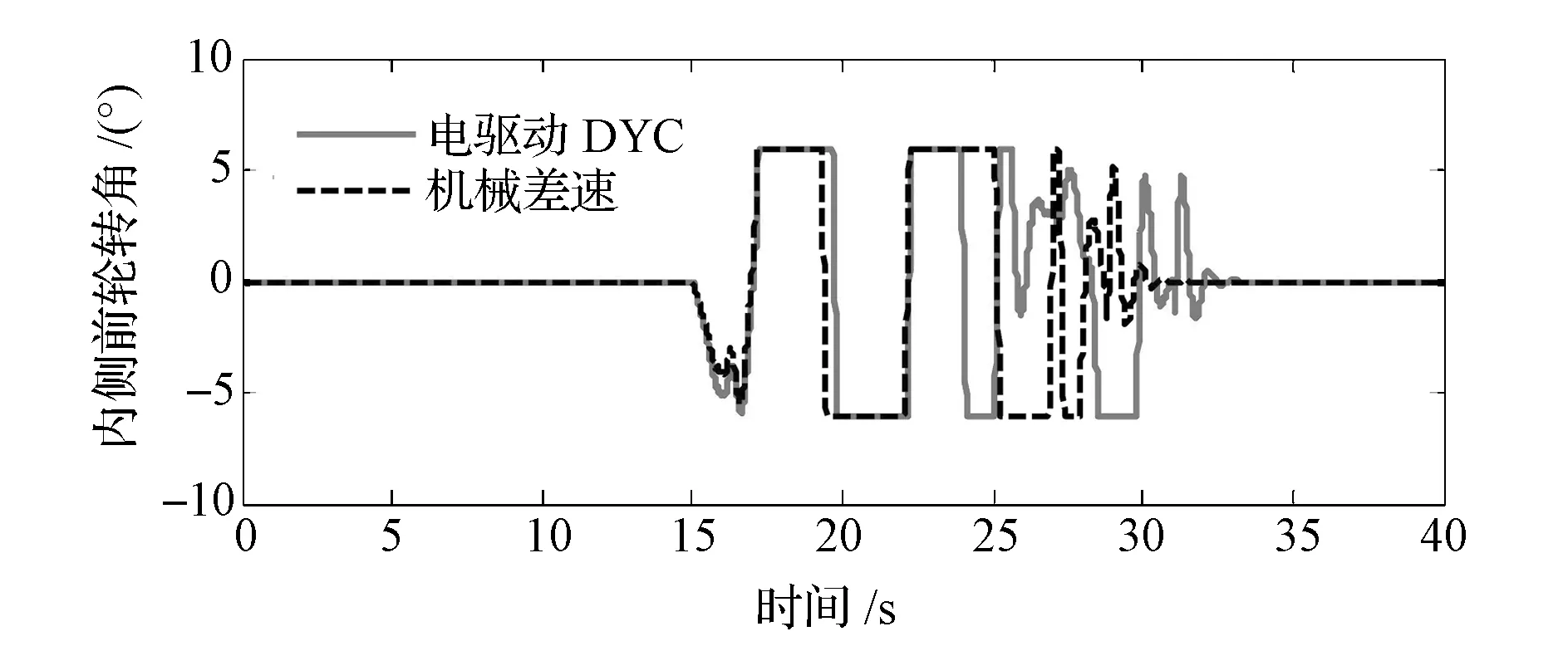
图10 闭环控制仿真的内侧前轮转角

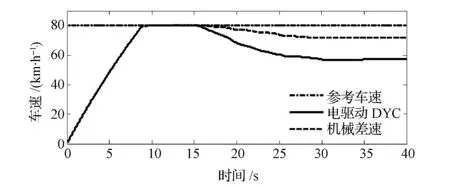
图11 闭环控制仿真的车速

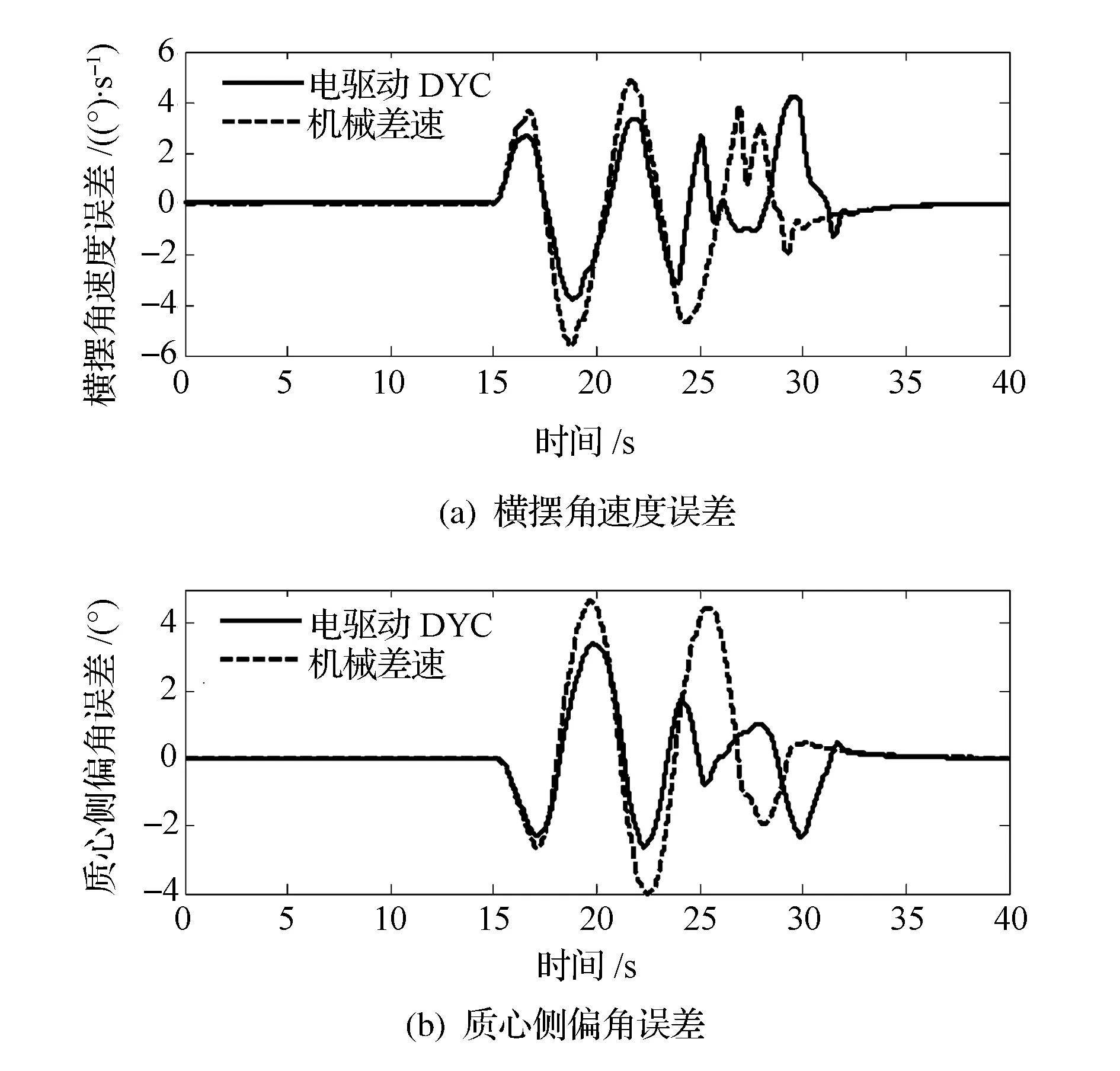
图12 闭环控制仿真的横摆角速度和质心侧偏角误差

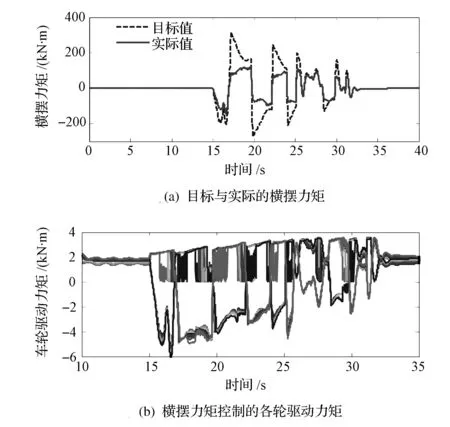
图13 闭环控制仿真的横摆力矩和各轮驱动力矩

图14 闭环控制仿真的行驶轨迹

4 结论

本文中针对多轴车辆高速行驶稳定性差的问题，充分利用电动轮各轮可独立控制的优势，建立了八轴车2自由度控制系统模型和整车三维动力学模型，设计了基于多参数变权重比例和最优控制算法的上层横摆力矩控制器，提出了一种基于规则的横摆力矩分配策略和一种基于车辆行驶安全的驱动力调整策略。

通过对驾驶员闭环系统的路径跟踪进行仿真，对横摆角速度和质心侧偏角的误差、实际输出横摆力矩，和行驶轨迹进行对比分析。结果表明，采用横摆力矩控制器降低了八轴车在高速转向行驶中的横摆角速度误差和质心侧偏角误差，二者分别降低了32%和22%以上；横摆力矩控制的效果受电机实际输出能力的限制；采用横摆力矩控制的多轴车辆能更准确地按照驾驶员给定的路径行驶，有效提高了多轴车辆高速行驶稳定性。

[1]KIMW,YIK,LEEJ.DriveControlAlgorithmforanIndependent8In-wheelMotorDriveVehicle[J].JournalofMechanicalScienceandTechnology, 2011, 25(6): 1573-1581.

[2]KIMWG,KANGJY,YIK.DriveControlSystemDesignforStabilityandManeuverabilityofa6WD/6WSVehicle[J].InternationalJournalofAutomotiveTechnology, 2011, 12(1): 67-74.

[3]SHINOM,NAGAIM.IndependentWheelTorqueControlofSmall-scaleElectricVehicleforHandlingandStabilityImprovement[J].JSAEReview, 2003, 24(4): 449-456.

[4] 王树凤, 李华师. 三轴车辆全轮转向最优控制[J]. 汽车工程, 2013, 35(8): 667-672.

[5] 申焱华, 李艳红, 金纯. 电驱动铰接式工程车辆操纵稳定性控制分析[J]. 农业工程学报, 2013, 29(12): 71-78.

[6] 张聪, 王振臣, 程菊, 等. 4WIS-4WID车辆横摆稳定性AFS+ARS+DYC滑模控制[J].汽车工程,2014,36(3):304-309.

[7] 宋宇, 陈无畏, 陈黎卿. 四轮转向车辆横摆角速度反馈与神经网络自适应混合控制的研究[J].汽车工程,2013,35(1):66-71.

[8]GENGC,MOSTEFAIL,DENAIM,etal.DirectYaw-momentControlofanIn-wheel-motoredElectricVehicleBasedonBodySlipAngleFuzzyObserver[J].IndustrialElectronics,IEEETransactionson, 2009, 56(5): 1411-1419.

[9]NAGAIM,HIRANOY,YAMANAKAS.IntegratedControlofActiveRearWheelSteeringandDirectYawMomentControl[J].VehicleSystemDynamics, 1997, 27(5-6): 357-370.

[10]KANGJY,YIK,NOHK.DevelopmentandValidationofaFinitePreviewOptimalControlBasedHumanDriverSteeringSodel[C].KSMESpringConference, 2007: 130-135.

Stability Control for Eight-axle Independent In-wheel Motor Drive Vehicle Considering the Effects of Steering Angle

Gao Yu1, Shen Yanhua1, Liu Xiangxin2& Wei Xuezhong2

1.SchoolofMechanicalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083;2.BeijingInstituteofSpaceLaunchTechnology,ChinaAcademyofLaunchVehicleTechnology,Beijing100076

In view of the poor stability of multi-axle vehicle with its rear axle involved in steering, the stability control of an eight-axle electric drive vehicle is studied in this paper. Firstly a yaw moment controller is designed based on variable weighting factors for multi-parameters and optimal control algorithm, and a rule-based yaw-moment distributing strategy and a vehicle driving safety-oriented driving force adjustment strategy are proposed with consideration on the effects of turning angle change in steering on the distribution of driving force. Then a 2 DOF control system model and a 3D vehicle dynamics model are established and an upper layer controller for calculating compensating yaw-moment and a lower layer controller for the driving force distribution between wheels are designed. Finally a simulation on the double lane change path tracking for closed-loop driver model is conducted. The results indicate that the vehicle stability controller established effectively improves the high-speed driving stability of eight-axle vehicle.

multi-axle vehicle; electric drive; stability control; yaw moment; driving force

*国家高技术研究发展计划(863计划)(2011AA060404)资助。

原稿收到日期为2014年11月19日，修改稿收到日期为2015年2月4日。