台车试验碰撞波形离散性及其对儿童约束系统响应影响的研究*

黄 毅,姬佩君,马令晨,周 青

(清华大学，汽车安全与节能国家重点实验室，北京 100084)

2016071

台车试验碰撞波形离散性及其对儿童约束系统响应影响的研究*

黄 毅,姬佩君,马令晨,周 青

(清华大学，汽车安全与节能国家重点实验室，北京 100084)

利用主成分分析法对台车试验时儿童乘员约束系统的碰撞波形进行分析，波形的离散性通过5个主成分进行量化。在MADYMO的环境中，以主成分反求的波形曲线作为约束系统的输入，研究了波形离散性对儿童假人头部和胸部响应的影响。结果表明，头部位移对波形的离散不敏感，而头部和胸部加速度的输出值受波形影响较大。本研究提供了一种试验波形离散性的量化方法，可用于儿童约束系统稳健性设计中的仿真。

汽车被动安全；儿童约束系统；台车试验；碰撞仿真；主成分分析

前言

台车碰撞试验是检验儿童乘员约束系统保护效果的主要方法之一。减速或加速台车的波形发生器对台车施加一个碰撞加速度历程，以模拟车辆在真实碰撞工况下，儿童约束系统和假人承受冲击的过程。儿童约束系统相关法规(ECE-R44，FMVSS213)均对该波形定义了一个许可区间[1-2]，来限制不同试验的冲击能量、强度的差异，使试验的结果具有一定的可比性。然而，在法规界定的区间内，波形仍会受到许多因素的影响而表现出较大的差异。由于约束系统和假人的非线性，在假人的响应上，这些差异可能会被放大。这将给儿童约束系统试验的评价和儿童约束系统的设计带来不利的影响。

随着计算机技术的发展，仿真已经成为约束系统研发的重要方法之一。在约束系统仿真中，通常将台车试验中测得的碰撞波形作为输入，研究约束系统和假人的响应。但由于计算机仿真是确定性的，不能反映真实试验中的随机现象[3]。文献[4]中研究了来自假人和约束系统参数设定等随机因素对假人损伤输出的影响。文献[5]中对约束系统台车试验波形的离散性进行量化分析，并研究波形离散性与假人损伤之间的相关性。还有不少的相关研究，皆旨在将随机现象包括在仿真系统中，使仿真可用于约束系统的稳健性分析。然而这些研究工作对波形的离散性分析，是获得多个试验波形的平均值，然后统计波形在每个时间点的方差，在平均波形的基础上形成一个离散区间。最后对平均波形进行比例缩放，得到一系列落于此区间内的新波形作为约束系统的输入。该方法存在的问题是忽略了波形在局部状态上的差异，同时也会放大波形能量产生的影响。

文献[6]中提出了使用主成分分析方法，来提取碰撞波形的特征，并研究车辆前端结构参数与波形特征之间的关系。文献[7]中则使用主成分分析方法对交通事故中碰撞事故数据记录仪(event data recorder, EDR)所采集的波形数据进行分析，并研究波形与碰撞形式之间的关系。与前述的基于均值的分析方法相比，基于主成分分析方法可在保留波形总体形状的同时，复现局部的波形振荡，更真实地反映波形的离散性及其对响应的关键影响源。

本文中采用主成分分析的方法，对某批儿童约束系统台车试验波形进行分析，并利用仿真模型，研究波形离散性对约束系统响应的影响，以期在试验波形控制和仿真设计中波形构建方面给出指导。

1 减速台车试验碰撞波形

图1 台车及减速装置

欧洲ECE-R44儿童约束系统测试法规中规定，试验台车可通过减速吸能装置来实现目标加速度波形，作为儿童约束系统的输入。法规中建议的一种减速装置如图1所示，其减速原理为台车上的橄榄头插入到固定在试验轨道末端的聚氨酯管中，通过橄榄头对聚氨酯管壁的摩擦和挤压，使台车减速[1]。

图2为某批共30次儿童座椅约束系统台车试验的碰撞波形。从图中可见，试验波形曲线基本全部落在法规界定的区间内。波形在整体形状上表现出较好的一致性，但在一些局部，仍存在不小的差异，例如波形第1峰的峰值和波形达到最大值的时间等。这些差异可能会对约束系统和假人的响应产生较大的影响。

图2 30次台车试验加速度波形以及ECE-R44法规的范围要求

2 基于主成分分析法的波形分析

本文中使用主成分分析法(principal component analysis, PCA)对波形的特征进行提取和参数化。主成分分析是一种多元数据分析方法，其主要的功能是对高维数据进行降维，同时尽可能多地保持原数据的特征。该方法常应用于图像压缩与识别，其核心的理念是分析数据方差之间的相关性[8]。具体的数据处理过程是，先对试验测得的加速度曲线进行重新采样，保证不同曲线的采样时间、间隔一致。在本文中，每条曲线经过重新采样后得到2 220个点。每条曲线的点形成一个向量xi(i=1,2,…,30)，每个向量有2 220个元素。将每条曲线减去平均曲线，形成新的向量x′i。对x′i求协方差矩阵C，并对C进行特征值分析，得到2 220个特征向量及其对应的特征值。根据特征值的大小，对特征向量进行排序，舍弃特征值较小的特征向量，剩下的特征向量组成一个新的矩阵F。可通过下式求得降维后的数据：

yi=FT×xi

(1)

本文中保留了特征值最大的5个特征向量,其对应的特征值以及标准差如表1所示。这5个特征向量可以代表原始数据90%的变差。其中P5的特征值最大，亦即曲线的离散性在P5上的表现最为明显[8]。

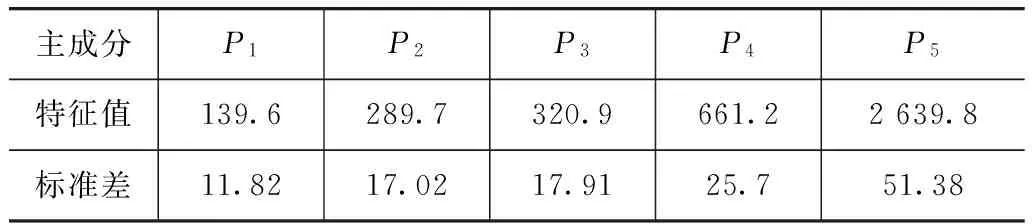
表1 波形主成分特征值及标准差

通过式(1)可以从降维后的数据“复现”原始的数据。由于矩阵F舍弃了一些特征向量，因而数据有所失真，如图3所示。

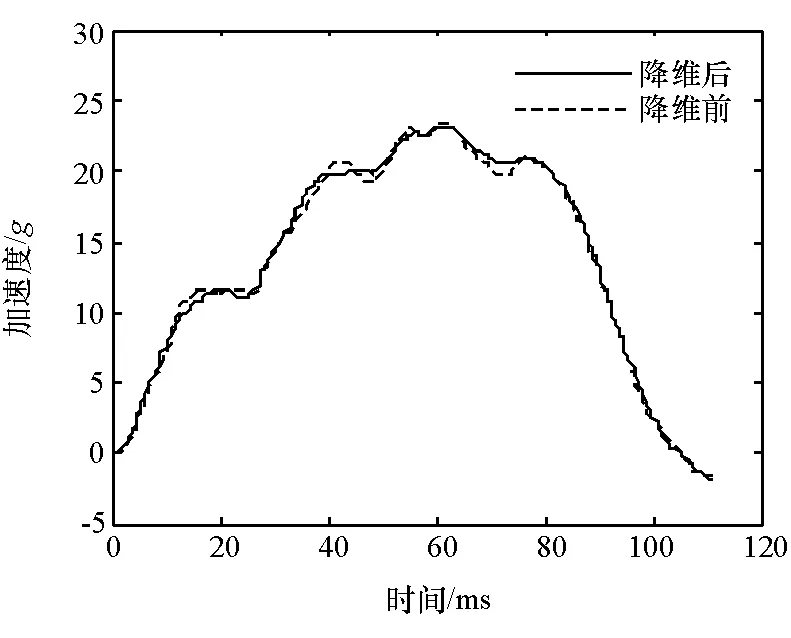
图3 某次试验加速度波形降维前后对比

图4显示了各个主成分对平均曲线的影响。由图可见，不同的主成分是对平均曲线进行不同形状的叠加，主要有以下几个特征：

P1影响第1峰附近局部的曲线；

P2影响第2峰后平台；

P3影响波形第1峰后的平台和波形达到最大值后的下降速度；

P4影响波形第1次上升斜率和第1峰值；

P5主要影响曲线2次上升斜率和总体峰值。

图4 主成分对平均曲线的影响

3 波形离散性对儿童假人损伤响应的 影响

为了研究波形差异对儿童假人损伤响应的影响，本文中使用了一个MADYMO模型作为研究对象[9](图5)。该模型针对汽车后排座椅环境建立，其中安全带、座椅、增高垫的材料参数由材料试验获得。模型中使用了MADYMO假人数据库中的Hybrid Ⅲ系列6岁多刚体假人模型。将台车加速度波形作为约束系统的输入，可获得假人及约束系统在冲击下的动态响应。

图5 儿童约束系统及Hybrid Ⅲ假人的MADYMO模型

为验证上述波形降维方法对约束系统和假人响应的影响，先以图3中所示的波形曲线分别输入到仿真模型中，对比假人头部、胸部和髋部的加速度响应(图6)。可见降维后所产生的波形失真不会对假人的损伤参数响应产生较大影响。

图6 降维前后假人头部、胸部和髋部加速度响应对比

为了研究波形差异对约束系统及假人响应的影响，本文中以表1所示的5个主成分的标准差的2倍作为相应参数取值的范围，使用Uniform Latin Hypercube方法在该范围内生成100个采样点，其波形曲线如图7所示，较好地落在法规区间内。这些曲线作为约束系统的输入，对假人的关键损伤输出和头部沿X方向相对车身的位移进行分析，结果如表2所示。由表可见：头部X方向位移的变化不大；基于加速度的输出，头部、胸部3ms加速度峰值和HIC受到的影响较大，其中HIC的变化幅度达43%。

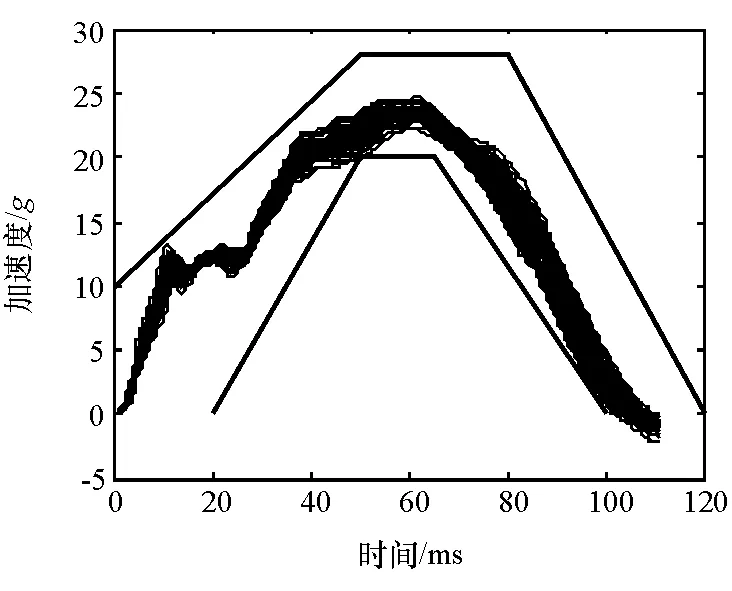
图7 由主成分生成的100个碰撞波形

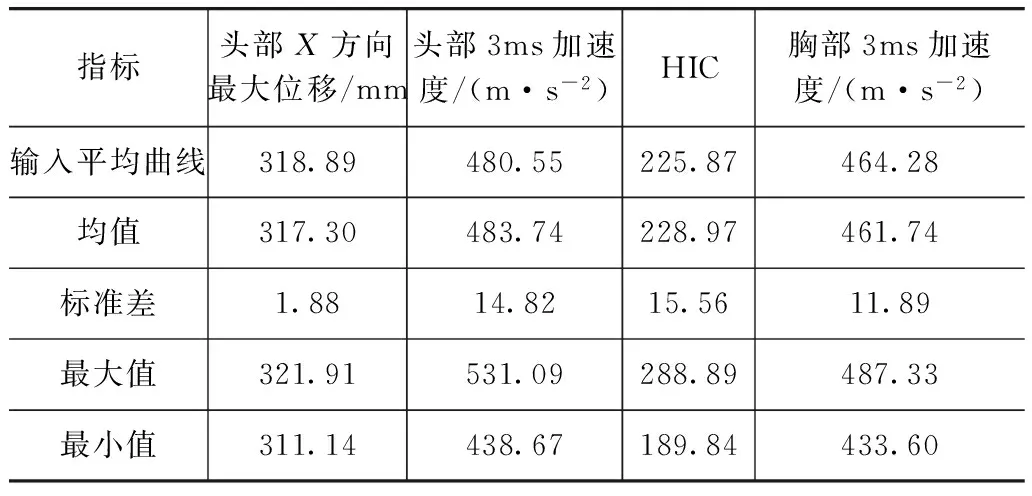
指标头部X方向最大位移/mm头部3ms加速度/(m·s-2)HIC胸部3ms加速度/(m·s-2)输入平均曲线318.89480.55225.87464.28均值317.30483.74228.97461.74标准差1.8814.8215.5611.89最大值321.91531.09288.89487.33最小值311.14438.67189.84433.60

表3为波形主成分与假人损伤参数响应的敏感性分析。其中P1与响应的相关性最不显著，这是因为P1所代表的曲线变差最小(图4(a))。值得注意的是，4个响应参数对P3均不敏感。从图4(c)上看，P3影响波形第1峰后的平台区，以及波形达到最大值后的下降速度。对响应产生较大影响的是P5,P4和P2。其中P2和P5对波形的峰值影响最明显，P4对波形的影响在于波形第1峰的上升斜率和峰值。

从100个生成的波形曲线中，挑选出对各个响应影响最大的曲线，结果如表4和图8所示。其中曲线42的胸部3ms加速度最大，曲线80的头部加速度和HIC响应最大，曲线81对应最大的头部位移。对于曲线42和80，其P2，P4和P5均取接近下限，使波形曲线在40ms后的平台值更高，且具有更大的峰值(图8)。曲线19所得的胸部加速度、头部加速度和HIC响应均为最小，其P2，P4和P5均接近其取值的上限。此时波形在40ms附近的平台值和波形峰值均比平均曲线小(图8)。由于头部最大位移对于各个主成分不敏感，此处曲线81和58并不能反映最坏情况所对应的主成分取值倾向。以上的结果与前面的主成分敏感性和效应分析的结果一致(表3)。

表3 主成分与约束系统响应的敏感性分析

表4 最差响应的波形主成分及假人输出

注：带*的数值为该响应的最差值；带**的数值为该响应的最佳值。

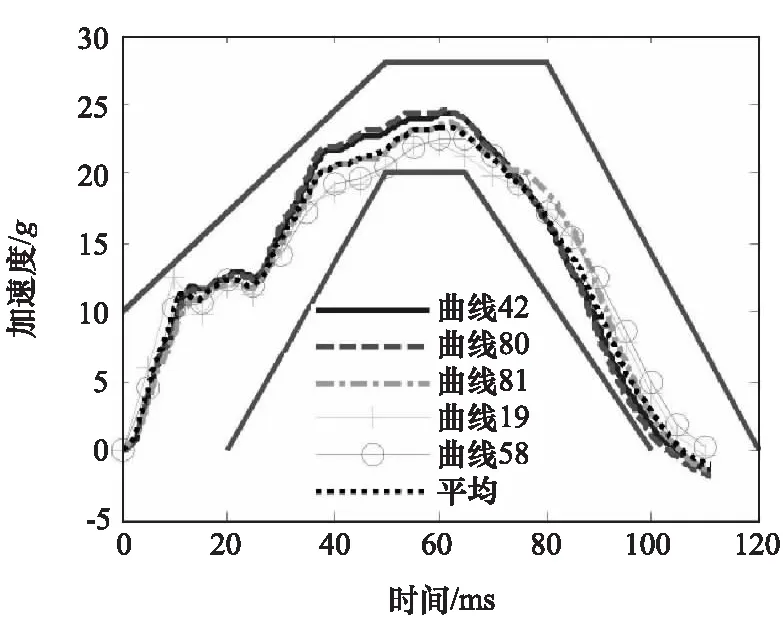
图8 影响最大波形曲线

4 讨论

传统波形曲线离散性描述的方法是将试验波形曲线的均值进行整体缩放，使之落于试验统计误差的区间之内[4,10],或者对波形曲线的特征进行简化，以简单的直线代替，并对直线的斜率进行控制[11]。前者无法反映波形局部振荡的变化；后者较注重于波形的变化机理，便于将波形的某段斜率与其背后的结构原因联系起来，但难以较全面地反映试验中波形所表现出的随机现象。本文中所采用的主成分分析法，较好地克服上面两个方法的缺点。如图4所示，波形的局部特征被很好地记录并复现，在仿真分析中，这些波形的局部特征差异因约束系统的强非线性，在某些假人响应，尤其是以加速度峰值为主的输出上得到放大，对约束系统的性能评价产生影响。

本文中的方法实际上是将台车试验波形曲线的离散性当作系统的随机误差来处理。从30条波形中提取的5个主成分值密度分布如图9所示。各个主成分的取值均集中于0附近，偏离0值情况出现的概率随着偏差增大而减小。可对数据进行正态分布的拟合，计算出分布的均值与方差。在进行儿童约束系统仿真分析时，可利用这些分布的信息，进行概率抽样，生成波形曲线，用于研究响应的分布，从而进行约束系统稳健性分析。另外，提取的波形主成分分布，可用于试验波形质量监控。例如，如果从后续试验的波形中提取的主成分明显偏离于现有的分布，则应检查台车和减速装置是否存在系统结构上的变化，从而产生系统误差。

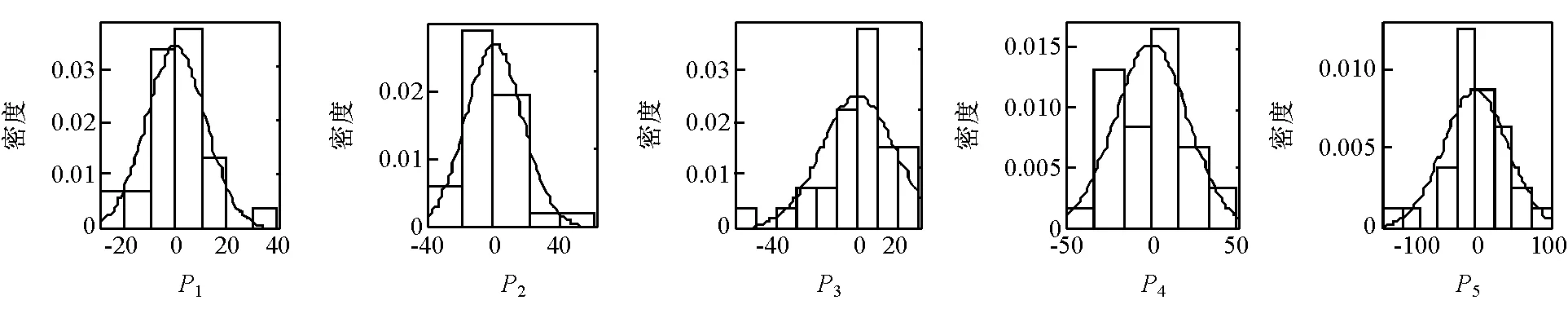
图9 30次台车试验波形提取的主成分的密度分布

在假人响应对波形离散性的敏感性分析中，头部和胸部对加速度的响应，如头部、胸部3ms加速度峰值和HIC的变化幅度较大。这些量取决于约束系统和假人系统的瞬态响应，碰撞波形在局部的差异，容易被该系统的强非线性所放大。头部最大位移响应是一个过程量，头部加速度的差异经过对时间两次积分后被缩小。因此，对于本文中所使用的儿童约束方式而言，在针对波形离散性的设计时，应优先考虑加速度响应值的优化，留出较大的余量，而对于头部位移的响应，由于受波形离散影响不大，可留出较小的余量。

5 结论

本文中利用主成分分析法对已有的儿童约束系统台车试验波形曲线进行分析。结果表明，对于本文试验所用的台车设备，只需提取5个特征量即可较好复现真实的波形。利用所提取的5个特征量，人为加入偏差，重新生成新的波形曲线，用作儿童约束系统仿真分析的输入，以研究响应变差与波形变差之间的关系。该方法与传统的基于均值和方差的波形离散性分析相比，能更真实地复现波形的主要形状特征，如波形达到峰值的时间(相差)等。分析结果显示，假人头部位移对波形的离散性不敏感。基于加速度的损伤输出，如头部、胸部3ms加速度峰值和HIC受到的影响较大。

利用本文中所介绍的方法对儿童约束系统碰撞试验的碰撞波形曲线进行分析，提取出主成分，可形成一个波形数据库。这个数据库记录了试验装置的合理误差。对于试验机构，波形主成分可作为波形离散性的量化指标，便于监测和控制试验波形的质量。对于儿童座椅厂商，通过波形主成分反求的波形曲线，可作为儿童约束系统仿真的输入，进行儿童约束系统产品的稳健性评估与设计，或者直接利用最坏情况的波形曲线，对约束系统的响应进行检验。

本文中的结论可能受限于仿真模型中所用的儿童约束的具体方式。后续可将该方法应用于其它的约束形式，研究响应与波形离散性的关系。

致谢

MADYMO软件教育版授权由TASS International公司提供，特此致谢。

[1] ECE R44 (Revision 2).[S].2008.

[2] FMVSS, Federal Motor Vehicle Safety Standard 213.[S].2009.

[3] NARAYAN Y, NAHUM A M, JOHN M. Accidental Injury-Biomechanics[M]. 3rded. Newyork: Springer Press,2015.

[4] DALENOORT A, GRIOTTO G, MOOI H, et al. A Stochastic Virtual Testing Approach in Vehicle Passive Safety Design: Effect of Scatter on Injury Response[C]. SAE Paper 2005-01-1763.

[5] MA D, ZHANG H. Evaluation of Frontal Occupant Protection System Responses to Crash Pulse Variations[J]. International Journal of Crashworthiness,2006,11:243-250.

[6] HOFFENSON S, REED M P, KAEWBAIDHOON Y, et al. On the Impact of the Regulatory Frontal Crash Test Speed on Optimal Vehicle Design and Road Traffic Injuries[J]. International Journal of Vehicle Design,2013,63:39-60.

[7] IRAEUS J, LINDQUIST M. Pulse Shape Analysis and Data Reduction of Real-Life Frontal Crashes with Modern Passenger Cars[J/OL]. International Journal of Crashworthiness,2015[2015-09-23]. http://dx.doi.org/10.1080/13588265.2015.1057005.

[8] JOLLIFFE I T. Principal Component Analysis[M]. 2nded. Newyork: Springer Press,2002.

[9] 唐亮,吴滔滔,周青,等.儿童乘员伤害指标及下潜趋势的影响因素[J].华南理工大学学报(自然科学版),2012(7):46-50.

[10] ROUX W, STANDER N, GÜNTHER F, et al. Stochastic Analysis of Highly Non-Linear Structures[J]. International Journal for Numerical Methods in Engineering,2006,65:1221-1242.

[11] CAO J Z, KOKA M R, LAW S E. Vehicle Pulse Shape Optimization to Improve Occupant Response in Frontal Impact[C]. SAE Paper 2004-01-1625.

A Study on Crash Waveform Dispersion and Its Effectson the Responses of Child Restraint System

Huang Yi, Ji Peijun, Ma Lingchen & Zhou Qing

TsinghuaUniversity,StateKeyLaboratoryofAutomotiveSafetyandEnergy,Beijing100084

Principal component analysis technique is used to analyze the crash waveforms of child restraint system in sled tests, in which the dispersion of waveform is quantified by five principal components. With the waveform curve solved out inversely by principal components as input, the effects of waveform dispersion on the head and chest responses of child dummy are studied in MADYMO environment. The results show that head displacement is not sensitive to waveform dispersion, while head and chest acceleration responses are influenced by waveform significantly. The study provides a method to quantify test waveform dispersion, which can be used for simulation in robustness design of child restraint system.

vehicle passive safety; child restraint system; sled test; crash simulation; principal component analysis

*国家自然科学基金(50975156)资助。

原稿收到日期为2015年10月13日，修改稿收到日期为2015年12月23日。