悬架运动学特性的区间可靠性控制*

麻 凯,高继东,谢书港

(1.天津大学机械工程学院，天津 300072； 2.中国汽车技术研究中心，天津 300300)

2016057

悬架运动学特性的区间可靠性控制*

麻 凯1,2,高继东2,谢书港2

(1.天津大学机械工程学院，天津 300072； 2.中国汽车技术研究中心，天津 300300)

本文中结合区间控制理论、概率论和可靠性理论，提出了计及硬点坐标不确定性的悬架运动学特性区间可靠性控制方法。该方法将与悬架运动学特性可靠性相关的硬点坐标参数区间作为控制对象，将悬架运动学特性区间可靠性作为控制目标，进行可靠性控制。最后，以前束角曲线和外倾角曲线为区间可靠性控制目标，灵敏度较高的硬点坐标区间作为区间控制参数，进行仿真。结果进一步验证了该方法的可行性。

悬架运动学特性；灵敏度分析；可靠性控制；区间控制；概率论

前言

近年来，随着产品质量标准的不断提高，对结构可靠性的控制成为研究的热点。工程中所有的机械结构都受到各种因素带来的不确定性影响，而这些不确定性可能来自于边界条件、结构尺寸和材料属性等因素，这些不确定因素会对结构的应力、应变、疲劳寿命和运动特性产生影响。这些影响对可靠性评估十分重要，不可忽略。在可靠性的控制中，结构的可靠性按照传统的定义方法规定为，在给定的可预期的使用环境下，结构完成预定工作的能力[1-2]。随着研究的深入，可靠性又被细化定义为概率可靠性和非概率可靠性，它们分别基于概率模型和非概率模型对结构可靠性进行研究。

基于概率论的可靠性研究已比较成熟。概率论即随机理论[3-5]，指在规定的使用环境下，机构完成指定工作的概率，在工程领域内它已经被广泛使用。而随着人们对不确定性认识的深入，随机方法被发现已经不能准确地描述所有的不确定性问题。因此,仅用概率方法研究可靠性问题是不够的。于是在该模型基础上，发展了不同的研究可靠性的方法，例如：灰色理论[6-7]、模糊理论[8-10]、凸模型理论[11-15]和区间理论[14-15]。并出现了使用以上两种及两种以上方法组合描述不确定性的可靠性分析方法[16-19]。这些方法弥补了用传统随机方法分析可靠性的不足。在各种描述不确定性的方法中，由于区间方法对数据样本信息量要求较低，用区间方法评价结构的可靠性得到了广泛应用。

文献[20]中提出通过控制悬架结构参数容差保证其运动学特性曲线的一致性的方法,提出利用区间方法建立悬架运动学特性曲线一致性的不确定性结构参数模型。它把悬架结构中参数容差看作不确定参数,即区间参数,通过区间控制方法控制其外特性的一致性。

本文中将区间控制方法与概率方法相结合，设计了一种新的可靠性控制方法，该方法可以控制目标的分布区间和分布规律。

本文中将所设计的方法应用在悬架运动学特性曲线可靠性控制中，提出了悬架运动学特性区间可靠性控制方法。使用该方法，设定合理的结构硬点坐标参数的中值和概率分布规律，达到控制悬架运动学特性可靠性的目的。

最后，通过某款车的双横臂悬架运动学特性曲线可靠性的控制，进一步证明了这种方法的可行性。

1 实数区间及其运算

(1)

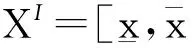
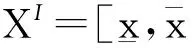
(2)

(3)

为区间XI的中值和半径，即不确定量。

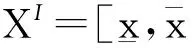
[XC,XC]+[-ΔX,ΔX]=XC+ΔXI=

XC+ΔX[-1,1]=XC+ΔXeΔ

(4)

式中：ΔXI=[-ΔX,ΔX]；eΔ=[-1,1]。这种表示方法称为区间的中心区间表示法。

2 区间控制方法

考虑3个函数f1(X),f2(X)和f3(X)，都含有4个自变量X=(x1,x2,x3,x4)，略去高阶项，1阶泰勒展开式为

(5)

可知,df1/dx1≈a1,df2/dx1≈a2,df3/dx1≈a3,当x1增量为Δx1=(df1/dx1)-1=1/a1,式(5)中的3个函数的增量Δf1,Δf2和Δf3可分别表示为

(6)

(7)

(8)

i=1,2,3,4；k=1,2,3

(9)

如果给定Δf1(X),Δf2(X),Δf3(X)，求满足条件的ΔX=(Δx1,Δx2,Δx3,Δx4)，则可利用式(10)先求出λ1,λ2,λ3。

(10)

再将求出的λ1,λ2,λ3代入式(11)，求出Δx1,Δx2,Δx3,Δx4。

(11)

通过上面提出的区间半径控制方法来实现区间控制，具体步骤如下。

步骤1：设一个极小值Δx，即初始的区间半径，差分计算函数灵敏度。

(12)

步骤2：计算

(13)

步骤3：用如下方程组求λ1,λ2,…,λm。

(14)

步骤4：计算

(15)

步骤5：计算

Δfk(X)=fk(X+ΔX)-fk(X)

(16)

如果‖Δfk(X)-Δfkmax(X)‖f≤ε，停止计算，(Δfkmax(X)为控制目标半径)，这时式(15)得到的Δx就是满足Δfkmax(X)要求的参数区间半径。否则，令xi=xi+Δxi，计算

(17)

并回到第2步继续迭代计算。这里，ε是一个给定的阈值。

3 正态分布

若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布，且其概率密度函数为

(18)

则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作X～N(μ,σ2)。

正态分布是有两个参数μ和σ2的连续型随机变量的分布，参数μ是服从正态分布的随机变量的均值，参数σ2是此随机变量的方差，所以正态分布记作N(μ,σ2)。服从正态分布的随机变量取离μ越近的值的概率越大，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。

σ描述正态分布数据分布的离散程度，σ越大，数据分布越分散；σ越小，数据分布越集中。也称为是正态分布的形状参数，σ越大，曲线越扁平；反之，σ越小，曲线越瘦高。

4 悬架运动学特性曲线区间可靠性控 制方法

在生产过程中，加工误差是不可避免的。要保证悬架运动学特性曲线的可靠性，必须合理控制加工精度，即保证一定比例的悬架运动学特性分布在给定的悬架运动学特性的不确定区间中。因为工程中硬点坐标和悬架运动学特性都满足正态分布X～N(μ,σ2)，所以σ可看作σ分布在[-σ,σ]区间，即σ也可视为区间参数。

因此，可靠性控制主要控制悬架运动学特性曲线分布范围fI=[-f,f]和分布率σI=[-σ,σ]，合并向量FI=[fI，σI]。悬架运动学特性曲线一般是一条参数随轮跳变化的曲线。控制这些曲线较理想的方法是控制曲线的两端。所以，本文中将对悬架运动学特性曲线的两个端点的分布区间和分布率控制来实现对悬架运动学特性可靠性的控制。主要步骤如下。

5 算例

以双横臂独立悬架模型为例，悬架模型和硬点名称见图1。控制前，前束角随轮跳而变化的曲线如图2所示，中间曲线为确定性参数下的悬架模型的前束角随轮跳变化曲线，另两条线为由结构参数容差引起的前束角随轮跳变化曲线的上下边界线，即曲线区间上界和下界。由于结构参数与前束角变化曲线具有单调性，且轮跳为零时，所有前束角的值相同，所以前束角边界曲线如果在轮跳正向为上边界时，在轮跳负向为下边界，另一条边界曲线相反。同理，外倾角随轮跳而变化的曲线如图3所示。

图1 双横臂独立悬架模型及控制点

图2 控制前双横臂独立悬架车轮前束角曲线区间

图3 控制前双横臂独立悬架车轮外倾角曲线区间

由结构的对称性，选取Z方向7对灵敏度最大的硬点坐标参数容差为要控制的区间参数的半径，见表1。初始参数下的前束曲线区间和尺度参数见表2，初始参数下的外倾曲线区间和尺度参数见表3。

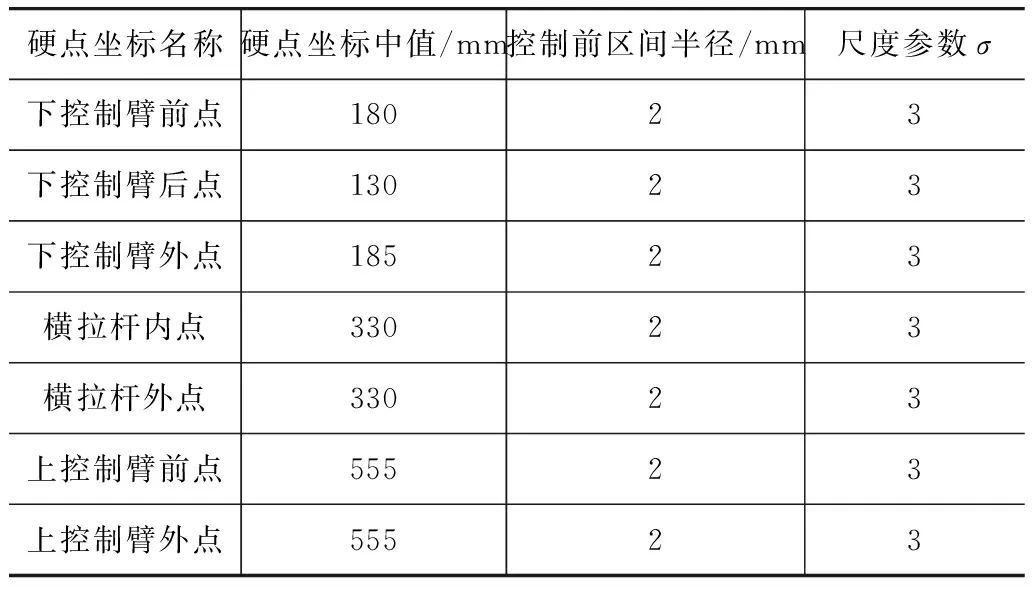
表1 控制前初始硬点坐标区间半径和尺度参数

表2 控制前的前束角区间半径和尺度参数

表3 控制前的外倾角区间半径

设计制造结构参数区间和各自尺度参数，控制悬架外特性一致性要求如下：

(1) 车轮前束角θtoe在轮跳-50mm～50mm变化区间为±0.05°，尺度参数为0.1；

(2) 车轮外倾角θcamber在轮跳-50mm～50mm变化区间为±0.05°，尺度参数为0.1。

通过对前束角和外倾角的灵敏度分析可知，同一区间参数下前束角和外倾角的区间半径都随轮跳增加而增大，所以控制前束角和外倾角曲线一致性时，可以通过控制正、负向最大轮跳点的前束角和外倾角来实现。

区间可靠性控制后结构参数区间半径和尺度参数见表4，前束角曲线区间见图4，外倾角曲线区间见图5，轮跳极值点前束角区间半径和尺度参数见表5，轮跳极值点外倾角区间半径和尺度参数见表6。

表4 控制后硬点坐标区间和尺度参数

图4 控制后双横臂独立悬架车轮前束角曲线区间

图5 控制后双横臂独立悬架车轮外倾角曲线区间

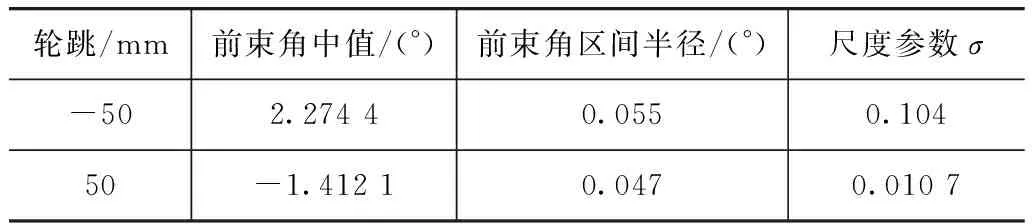
轮跳/mm前束角中值/(°)前束角区间半径/(°)尺度参数σ-502.27440.0550.10450-1.41210.0470.0107

表6 控制后的外倾角区间半径和尺度参数

从结果可以看出，控制后前束曲线和外倾曲线都在目标区间范围内，其分布规律也满足控制要求。因此，所有控制目标均满足区间可靠性控制要求。

6 结论

本文中将区间控制理论与概率论相结合，建立应用于工程的区间可靠性方法，并应用该方法合理设计汽车悬架硬点的坐标区间和均方差，从而保证了悬架运动学特性的区间和分布规律，实现了可靠性控制。算例中通过对双横臂独立前悬架前束角和外倾角的区间可靠性控制，进一步说明了这种区间可靠性控制方法是可行的。

[1] 董聪.现代结构系统可靠性理论及其应用[M].北京:科学出版社,2001.

[2] ELISHAKOFF I. Discussion on: A Non-probabilistic Concept of Reliability[J]. Structural Safety,1995,17(3):195-199.

[3] 吕震宙,冯蕴雯.结构可靠性问题研究的若干进展[J].力学进展,2000,30(1):21-28.

[4] ZHAO Y G, LU Z J. Fourth-moment Standardization for Structural Reliabilityassessment[J]. J Struct Eng,2007,133(7):916-924.

[5] ZHAO Y G, ONO T. A General Procedure for First/second-order Reliabilitymethod[J]. Structural Safety,1999,21(2):95-112.

[6] 肖芳淳.复合材料结构灰色可靠性分析与设计[J].强度与环境,2000(1):60-65.

[7] 段齐骏,张福祥.复杂系统可靠性研究中的灰色问题[J].系统工程理论与实践,1999,119(12):96-98.

[8] HELTON J C, OBERKAMPF W L. Alternative Representations of Epistemicuncertainty[J]. Reliability Engineering & System Safety,2004,85(1-3):1-10.

[9] KLIR G J, SMITH R M. On Measuring Uncertainty and Uncertainty-basedinformation: Recent Developments[J]. Annal Math Art Int,2001,32(1-4):5-33.

[10] BERND M. Discussion on: Structural Reliability Analysis Through Fuzzynumber Approach, with Application to Stability[J]. Computers & Structures,2004,82(2-3):325-327.

[11] BEN-HAIM Y. A Non-probabilistic Concept of Reliability[J]. Structural Safety,1994,14(4):227-245.

[12] BEN-HAIM Y. A Non-probabilistic Measure of Reliability of Linear Systemsbased on Expansion of Convex Models[J]. Structural Safety,1995,17(2):91-109.

[13] AU F, CHENG Y S, LG THAM E A. Robust Design of Structures Usingconvex Models[J]. Computers & Structures,2003,81(28-29):2611-2619.

[14] 郭书祥,吕震宙,冯元生.基于区间分析的结构非概率可靠性模型[J].计算力学学报,2001,18(1):56-60.

[15] 王登刚,李杰.结构可靠性分析的区间方法[C].第12届全国反应堆结构力学会议论文专辑,2002:244-247.

[16] 董玉革.随机应力模糊强度时机械零件模糊可靠性设计方法的研究[J].机械设计,1999,16(3):11-13.

[17] 黄洪钟,孙占全,郭东明,等.随机应力模糊强度时模糊可靠性的计算理论[J].机械强度,2001,23(3):305-307.

[18] 麻凯,陈塑寰.结构区间参数的二阶近似动态优化方法[J].东北大学学报(科学版),2008(S2):400-405.

[19] JIANG Chao, LIU Lixin, TANG Yifei. A Structural Reliability Analysis Method for Hybrid Model with Interval Variables[J]. Automotive Engineering,2012(34):727-732.

[20] 麻凯,管欣,逄淑一,等.悬架运动学特性一致性区间控制方法[J].吉林大学学报(工学版),2011,4(41):910-914.

Interval Reliability Control for Suspension Kinematic Characteristics

Ma Kai1,2, Gao Jidong2& Xie Shugang2

1.SchoolofMechanicalEngineering,TianjinUniversity,Tianjin300072; 2.ChinaAutomotiveTechnology&ResearchCenter,Tianjin300300

By combining the theories of interval control, probability and reliability, an interval reliability control method for suspension kinematic characteristics is proposed with consideration of the uncertainty of hard point coordinates in this paper. In the method, reliability control is performed with the interval of hard point coordinate parameters related to the reliability of suspension kinematic characteristics as control object, and the interval reliability of suspension kinematic characteristics as control objective. Finally a specific simulation is conducted with toe-in angle and camber angle curves as the objectives of interval reliability control and the interval of hard point coordinates with higher sensibility as interval control parameters. The results further verify the feasibility of the method proposed.

suspension kinematic characteristics; sensitivity analysis; reliability control; interval control; probability theory

*吉林省科技厅青年科研基金(20130522180JH)资助。

原稿收到日期为2015年7月15日。