基于区间分析的汽车盘式制动器的稳定性分析与改进*

吕 辉，于德介

(湖南大学,汽车车身先进设计制造国家重点实验室，长沙 410082)

2016051

基于区间分析的汽车盘式制动器的稳定性分析与改进*

吕 辉，于德介

(湖南大学,汽车车身先进设计制造国家重点实验室，长沙 410082)

针对汽车制动噪声的抑制问题，基于区间不确定性分析，提出了一种汽车盘式制动器的稳定性分析与改进方法。该方法将制动器系统的摩擦因数、制动压力和磨损部件的厚度视为不确定性参数，并采用区间参数进行描述。以不稳定模态的阻尼比衡量系统的稳定性，将有限元复模态分析技术与响应面法相结合，建立了分析目标与系统参数间的隐式函数关系，实现了制动器稳定性分析模型的参数化。结合区间分析方法和可靠性分析方法，研究了某型车的盘式制动器系统的稳定性，分析了不确定性条件下制动器系统稳定性变化的统计规律，并从可靠性角度提出了改善系统稳定性的措施。该分析方法可为抑制制动噪声提供参考。

制动噪声；区间分析；稳定性；不确定性；复模态

前言

汽车制动噪声已成为城市的主要噪声污染源之一。如果汽车的制动器系统在工作过程中处于不稳定状态，就可能引起强烈的振动，并产生刺耳的噪声，其中以1～16kHz的尖叫声最困扰乘客的听觉，严重影响汽车的舒适性[1]。针对汽车制动噪声问题，不少研究通过对制动器摩擦耦合系统的有限元模型求解复模态来判断系统的稳定性，从而预测制动噪声的产生趋势。有限元分析已成为研究制动器稳定性的有效方法[2]。文献[3]中建立了汽车盘式制动器的摩擦耦合有限元模型，通过求解制动器的复模态，根据复模态的阻尼比分析了各参数对系统稳定性的影响，提出了降低摩擦因数和修改制动片几何形状的改善措施，该研究在汽车盘式制动器制动噪声的预估和改善上取得了很好的效果,但没有考虑参数不确定性的影响，研究结论只有在系统参数为确定值时才具有较大的参考意义。文献[4]和文献[5]中从子结构模态的角度对制动器的稳定性进行研究，基于制动器摩擦闭环耦合有限元模型求解了系统复模态，分析了模态参数的灵敏度，提出了修改支撑支架等改进措施，该研究方法没有考虑制动器磨损部件几何参数的变化和制动压力的波动变化，在实际工程中适用范围有限。

材料特性、几何磨损和作用载荷等参数在工程实际中往往具有不确定性，将各参数的不确定性引入分析模型中，能更好地反映工程实际[6]。将不确定性参数看作区间参数，只须获得参数的上下界信息，这些信息在工程实际中也很容易获得，因此基于区间分析的相关研究在工程中得到了广泛的应用[7]。将不确定性参数引入分析模型后进行可靠性分析，能保证随机模型不因参数的波动而失效[8]。

本文中针对制动器振动噪声产生的复杂性，将参数不确定性引入到汽车盘式制动器的稳定性分析中，采用区间参数对制动器系统的摩擦因数、制动压力和磨损部件几何厚度参数的不确定性进行描述，将有限元复模态技术和响应面法相结合，解决了分析目标与分析参数间的隐式函数关系问题，实现了制动器稳定性有限元模型的参数化。结合区间分析与可靠性分析，研究了某型车的浮钳盘式制动器系统的稳定性，分析了不确定性条件下该制动器稳定性变化的统计规律，并从可靠性角度提出了改善系统稳定性的措施。

1 区间参数和非概率可靠性

1.1 区间参数

对于任意不确定参数X在某一区间内变化，其上下界分别为XU和XL，即

X∈[XL,XU]

(1)

则称X为区间参数，令

(2)

式中：XC称为区间中点或均值；XR称为区间半径或离差。

1.2 非概率可靠性

受各种客观因素的影响，结构所受的载荷和结构的几何尺寸等参数往往都具有不确定性。如果这些参数的概率分布信息难以获取，但却能确定其大致变化范围，则可用区间变量描述这些参数。由于结构参数不包含概率信息，对应的结构可靠性称为非概率可靠性[9]。

设矢量X表示结构的不确定区间参数集合，即

(3)

式中:上标L和U分别表示下界和上界；m为区间参数个数。结构失效准则确定的功能函数为

M=G(X)=G{X1,X2,…,Xm}

(4)

功能函数M也为区间变量，即

M∈[ML,MU]

(5)

式中：MU和ML分别为区间上下界，且满足：

(6)

设M的均值和离差分别为MC和MR，定义结构的非概率可靠性指标[9]为

(7)

按照结构的可靠性理论，超曲面G(X)=0为失效临界面，它将结构的基本参量空间分为失效域和安全域，G(X)>0和G(X)<0分别表示结构处于安全状态和失效状态。

由式(4)和式(7)可知：如果η>1，均有G(X)>0，结构安全可靠；如果η<-1，均有G(X)<0，结构失效；如果-1<η<1，G(X)>0和G(X)<0均有可能，结构可能安全也可能失效。因此要保证结构完全可靠，必须保证η>1，η的值越大，结构的安全程度和可靠性越高。

2 盘式制动器稳定性的有限元分析

[10]，采用复特征值分析方法对制动器系统稳定性进行研究，振动系统的动力学方程为

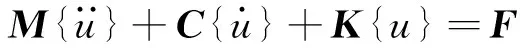
(8)

式中：M，C和K分别为振动系统的质量、阻尼和刚度矩阵；{u}为广义位移振动矢量；F为制动片和制动盘摩擦接触而产生的作用力矢量。将F简化为振动位移的线性函数[10]，并表示为

F=Kf{u}

(9)

式中：Kf为摩擦接触刚度矩阵，由摩擦接触面属性决定。将式(9)代入式(8)得自由振动方程：

(10)

由于引入了摩擦力，式(10)中的系统刚度矩阵(K-Kf)变为不对称结构，意味着系统特征根和特征向量在一定条件下是复数，对应有限元分析中系统模态频率和模态振型均为复数形式。

设振动系统的解为

{u}={φ}est

(11)

代入式(10)可转化为复特征值问题：

(s2M+sC+K-Kf){φ}=0

(12)

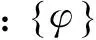
si1,2=σi±jωi

(13)

式中：σi和ωi分别为第i阶复模态对应的复特征值的实部和虚部。参考文献[3]，定义第i阶模态阻尼比的形式为

(14)

式中ζi为第i阶模态阻尼比。当阻尼比为负时，系统为负阻尼，系统特征值具有正实部，结合系统稳定性理论知此时系统是不稳定的；文献[3]表明负阻尼比ζi的数值越大，系统的稳定程度越高。因此系统的稳定性和稳定程度可通过ζi衡量。

3 汽车盘式制动器稳定性分析模型

3.1 汽车盘式制动器简化模型

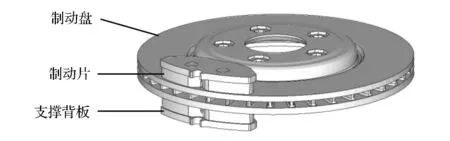
图1 盘式制动器简化模型

汽车盘式制动器一般由制动盘、制动片、支撑背板、钳体、分泵和油管等组成。为减小计算工作量，且能真实模拟制动器的振动特性，本文中建立了某国产轿车的盘式制动器简化模型，如图1所示。该简化模型与文献[3]、文献[6]、文献[10]和文献[11]的研究模型类似，已被成功应用于制动噪声领域的研究，模型的有效性已得到验证，并且取得了很好的研究成果。该简化模型主要包括制动盘、制动片和支撑背板等部件。

3.2 响应面方法

采用有限元复特征值分析方法对汽车盘式制动器系统的稳定性进行研究。以不稳定模态的负阻尼比衡量系统的稳定性，提高不稳定模态的负阻尼比，可有效改善系统的稳定性。制动器系统的各类参数(如摩擦因数和几何参数)均有可能对系统模态产生影响，因此通过某些参数的优化，往往能达到改善系统稳定性的目的。在传统的制动器系统有限元优化设计中，往往是假设某个设计参数变化，而其他设计参数保持某特定取值时，观察系统响应的变化[3]。显然，这种方法既耗时，又没有考虑参数间的交互作用，有一定的局限性。响应面方法[12]是一种构建近似模型的方法，它通过对指定设计空间进行试验设计，拟合输出变量(系统响应)与多个输入变量(系统输入)的关系。用响应面模型近似模拟设计变量和响应的映射关系，从而避免对复杂有限元模型的重复调用，减少运算次数，提高运算效率。

在制动器系统有限元分析中，系统的模态参数与系统参数的关系是一种典型的隐式函数关系。引入响应面法，可通过较少的有限元试验次数，拟合出系统不稳定模态参数与系统参数间的近似数学表达式。以系统不稳定模态为研究对象，参考文献[13]构建二阶响应面近似模型。与第k阶不稳定模态对应的复特征值实部和虚部的二阶多项式表达式为

(15)

(16)

式中:σk(x)和ωk(x)分别为复特征值的实部和虚部；a0,b0,ai,bi,aii,bii,aij和bij为未知系数，可通过试验设计和最小二乘法求解；xi(i=1,2,…,n) 为系统参数，n为系统参数个数。

得到响应面近似模型后，为了保证拟合模型的精度，须要对模型进行方差分析，进行精度检验。具体过程可参见文献[12]。

3.3 制动器的稳定性分析模型

由于制动器工作环境复杂多变，制动噪声的产生具有很大的不确定性，难以捕捉和重复，是很多不确定参数共同影响的结果，因此制动噪声的产生机理至今没有得到全面的认识。制动器系统参数的不确定性主要表现为：摩擦因数随相对滑动速度而改变；摩擦作用力和制动压力具有时变特性，表现为波动变化；制动片和制动盘在工作过程中不断磨损，几何厚度不断减小。

针对系统参数具有不确定性的问题，在参数信息比较匮乏的情况下，本文中采用区间参数对其进行描述，并用试验设计和随机模拟的统计方法进行分析。其中区间参数的取值情况见表1。

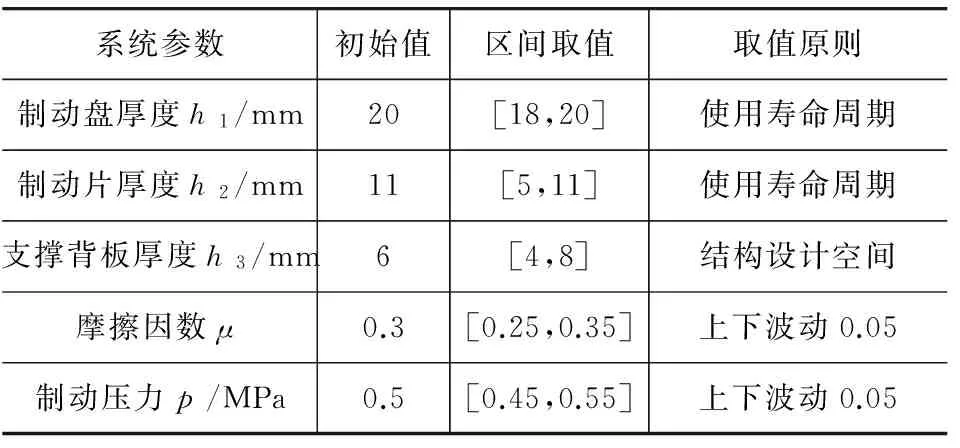
表1 制动器系统参数初始值和区间取值

采用有限元方法进行分析，首先建立制动器系统的有限元模型，如图2所示。模型共有26 125个实体单元，37 043个节点，制动片与制动盘之间为摩擦接触面，整个系统为一个摩擦耦合系统。

图2 制动器有限元模型

图3 有限元模型的边界条件

有限元模型的边界条件如图3所示。其中制动盘5个螺纹孔的中心被完全约束，但能随车轮一起绕盘中心轴线旋转；制动片与支撑背板牢固地粘在一起，制动压力均匀地加载在背板与液压缸对应的接触位置上，并假设加载在两个背板上的制动压力大小相等；支撑背板只能沿垂直于盘面的方向移动。 为便于进行试验设计和构造响应面近似模型，对表1中的区间参数进行归一化：

(17)

采用拉丁超立方试验设计方法[13]，在表1的区间参数组成的空间中获取了35组样本点，分别运用有限元方法计算制动器系统在0～16kHz范围内的复模态分布情况。结果显示，对应各组样本点系统的第7阶模态均为复模态，且其对应的复特征值实部均大于0，为不稳定模态；个别样本点还在其它阶数上出现不稳定模态，但其对应的阻尼比基本都大于第7阶。因此，第7阶复模态最不稳定，故本文中选取该阶模态为对象进行分析。

根据拉丁超立方试验设计的结果，结合最小二乘法，构造第7阶复模态的二次多项式响应面近似函数为

σ7=7.35+15.11x1+42.91x2+37.82x3+

4.81x4+0.71x5+13.68x1x2+12.13x1x3+

10.78x1x4-26.48x1x5+38.64x2x3-13.58x2x4+

21.31x2x5+19.21x3x4-6.09x3x5+9.64x4x5-

(18)

ω7=1832.19+156.54x1-11.62x2-0.051x3+

12.26x4-3.50x5-4.53x1x2-12.01x1x3-

5.43x1x4+1.62x1x5-8.15x2x3+5.38x2x4-

1.42x2x5-10.61x3x4+0.15x3x5-0.53x4x5-

(19)

式中：σ7和ω7分别为第7阶复模态对应的复特征值的实部和虚部。

按文献[10]中的方法对式(18)和式(19)的响应面模型进行显著性分析，可得响应面模型的不可靠概率小于1%，可用于后续分析研究。

4 制动器的稳定性分析与改进

4.1 汽车盘式制动器的可靠性分析模型

取不稳定模态负阻尼比大于某一常数值ζc时，系统可视为稳定状态。参考文献[15]，取ζc=-0.01，以第7阶复模态为研究对象，结合式(4)和式(14)可得系统稳定的可靠性功能函数为

(20)

引入可靠性的概念对不确定性条件下制动器系统的稳定性进行研究，结合式(6)、式(7)和式(20)，可得系统稳定的可靠指标为

(21)

制动器振动噪声发生具有强不确定性，适合采用随机模拟和统计试验方法进行分析。蒙特卡洛法是一种通过大量的随机抽样即可获取较高的求解精度的统计试验法，具有很强的适用性[6]，故本文中采用该方法进行分析。

4.2 汽车盘式制动器的稳定性分析

在表1的5个系统参数中，只有支撑背板厚度是可控制的设计参数，其它4个参数在制动器工作过程中都具有不确定性，难以控制。取背板厚度初值h3=6mm，其它参数取表1的区间值，进行摩擦因数和制动压力不确定性的研究。制动器系统的稳定性随磨损部件厚度变化的统计规律曲线如图4所示。

图4 不确定性条件下制动器稳定性的统计规律曲线

图4中各统计规律曲线并不是该制动器真实情况的模拟，而是综合考虑了所有不确定性参数共同作用下的数理统计结果，是最为保守的情况预估。例如图4(a)中功能函数随制动盘厚度的变化曲线，是该制动器的制动盘在各磨损厚度下，分别考虑摩擦因数和制动压力的不确定性、制动片厚度在整个磨损区间变化的不确定性得到的上下限值。由于分析过程中没有考虑磨损引起的系统参数间的相关性，因此分析结果是相对保守的。

从图4可以得出该制动器系统的稳定性在不确定因素影响下的统计规律：该制动器的稳定性随制动盘的磨损平稳地上下波动，没有明显的变化趋势；而随制动片的磨损，系统的稳定性有比较明显的变化。因此在工程设计中可以对制动盘厚度磨损的不确定性控制适当放宽，以降低成本；而对于制动片厚度磨损对系统稳定性的影响，在设计中要重点考虑和控制。

4.3 汽车盘式制动器的稳定性提高

对于背板厚度，除了加工时尺寸公差引起的微小不确定性外，其厚度在制动器的工作过程中是确定可控制的，适合作为设计变量。根据表1取背板厚度的设计范围为[4,8]mm，其它不确定参数取表1的区间值，在摩擦因数、制动压力和磨损部件几何厚度的不确定性共同作用下，该制动器系统的稳定性随背板厚度变化的统计规律曲线如图5所示。

图5 不确定性条件下制动器稳定性随支撑背板厚度变化的统计规律曲线

由图5(b)可知，支撑背板厚度h3<4.25mm和h3>7.3mm时，均有可靠性指标η>1，系统在不确定性因素的影响下达到稳定性要求的可靠度为100%。由于背板厚度初值h3=6mm，所以当h3<4.5mm时，结构刚度和强度不一定能得到保证，导致制动功能可能失效，因此可选择背板设计厚度h3>7.3mm作为改善该制动器振动性能的措施。

为了验证改善措施的有效性，在其它参数均取表1初始值的情况下，将h3=6mm和h3=7.3mm分别代入有限元模型，计算0～16kHz范围内系统的复特征值分布，对比结果如图6所示。从图中可以看出，当背板厚度h3=7.3mm时，系统不稳定模态对应的复特征值实部更小，模态负阻尼比更大，稳定性更高。

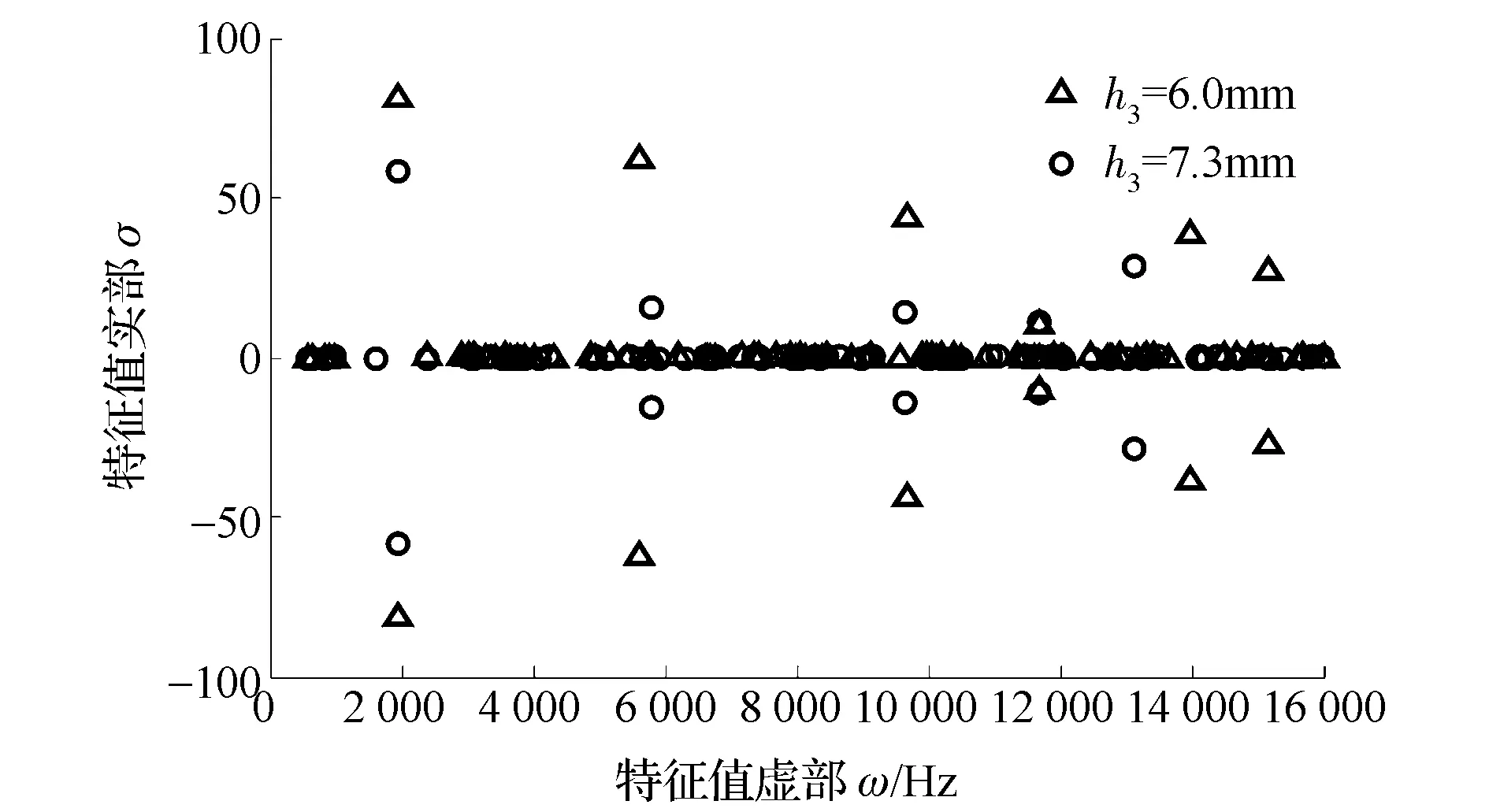
图6 不同背板厚度下系统的复特征值分布

5 结论

(1)针对制动噪声产生的复杂性，将参数不确定性引入到汽车盘式制动器的稳定性分析中，采用区间参数对制动器系统的摩擦力、制动压力和磨损部件的几何参数的不确定性进行描述，将有限元复特征技术与响应面法相结合，解决了分析目标与参数间的隐式函数关系问题，实现了制动器稳定性有限元模型的参数化。

(2)结合区间分析与可靠性分析，研究了某型车的盘式制动器系统的稳定性。分析了不确定性条件下，系统稳定性变化的统计规律，并从可靠性角度提出了改善系统稳定性的工程措施，对抑制制动噪声具有一定的工程指导意义。

参考文献

[1]PAPINNIEMIA，LAIJCS，ZHAOJ，etal.BrakeSqueal：aLiteratureReview[J].AppliedAcoustics， 2002，63(4) : 391-400.

[2]FRITZG，SINOUJJ，DUFFALJ，etal.EffectsofDampingonBrakeSquealCoalescencePatternsApplicationonaFiniteElementModel[J].MechanicsResearchCommunication，2007，34(2).

[3]LIUP，ZHENGH，CAIC.AnalysisofDiscBrakeSquealUsingtheComplexEigenvalueMethod[J].AppliedAcoustics，2007，68(6).

[4]GUANDihua，SUXindong，ZHANGFang.SensitivityAnalysisofBrakeSquealTendencytoSubstructuresModalParameters[J].JournalofSoundandVibration，2006，291(1)：72-80.

[5] 宿新东，管迪华. 利用子结构动态特性优化设计抑制制动器尖叫[J]. 汽车工程，2003，25(2)：167-170.

[6]SARROUYE，DESSOMBZO，SINOUJJ.PiecewisePolynomialChaosExpansionwithanApplicationtoBrakeSquealofaLinearBrakeSystem[J].JournalofSoundandVibration，2013，332(3-4)：577-594.

[7]MOORER，LODWICKW.IntervalAnalysisandFuzzySetTheory[J].FuzzySetsandSystems，2003， 135 (1)：5-9.

[8]RACKWITZR.ReliabilityAnalysis-aReviewandSomePerspectives[J].StructuralSafety，2001，23(4)： 365-395.

[9]HAIMYB.ANon-probabilisticConceptofReliability[J].StructuralSafety，1994，14 (4)：227-245.

[10]JUNIORMT，GERGESSN，JORDANR.AnalysisofBrakeSquealNoiseUsingtheFiniteElementMethod[J].AppliedAcoustics，2008，69(2)：147-162.

[11]ABUBAKARAR,OUYANGHJ.ComplexEigenvalueAnalysisandDynamicTransientAnalysisinPredictingDiscBrakeSqueal[J].InternationalJournalofVehicleNoiseandVibration， 2006， 2 (2)：143-155.

[12]MYERSRH,MONTGMERYDC,ANDERSONCM.ResponseSurfaceMethodologyProcessandProductOptimizationUsingDesignedExperiment[M].NewYork：WileyPublishers, 2009.

[13]NOUBYM,MATHIVANAND,SRINIVASANK.ACombinedApproachofComplexEigenvalueAnalysisandDesignofExperiments(DOE)toStudyDiscBrakeSqueal[J].InternationalJournalofEngineering,ScienceandTechnology, 2009, 1(1)：254-271.

[14]PAPILLAM.AccuracyofResponseSurfaceApproximationsforWeightEquationsBasedonStructuralOptimization[D].Gainesville：UniversityofFlorida，2001.

[15]HOUJun，GUOXuexun，TANGangfeng.ComplexModeAnalysisonDiscBrakeSquealandDesignImprovement[C].SAEPaper2009-01-2101.

[16]MELCHERSRE，AHAMMEDM.AFastApproximateMethodforParameterSensitivityEstimationinMonteCarloStructuralReliability[J].ComputersandStructures，2004，82(1)：55-61.

Stability Analysis and Improvement of Automotive Disc BrakeBased on Interval Analysis

Lü Hui & Yu Dejie

HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082

To suppress brake squeal, a stability analysis and improvement method of automotive disc brake system is presented based on interval uncertainty analysis. In the method proposed, friction coefficient, braking pressure and the thicknesses of wearing components are treated as uncertain parameters and described by interval variables. With the damping ratio of unstable modes as the indicator of system stability, and combining complex modal analysis with response surface method, the implicit function relationship between analysis objective and system parameters is established, achieving model parameterization for brake stability analysis. Furthermore, by combining interval analysis with reliability analysis, the disc brake stability of a vehicle is investigated, the statistical regularities of brake stability variation in uncertainty condition is analyzed, with the measures for improving brake system stability put forward from a perspective of reliability. The method proposed provides a reference for brake squeal suppression.

brake squeal; interval analysis; stability; uncertainty; complex mode

*湖南省研究生科研创新项目(CX2013B143)、湖南大学汽车车身先进设计制造国家重点实验室自主课题(71375004)和长沙市科技计划重大专项(K1306007-11-1)资助。

原稿收到日期为2014年10月8日，修改稿收到日期为2014年12月24日。