汽车盘式制动器蠕动颤振试验与理论分析*

张立军，张频捷，孟德建

(同济大学汽车学院，上海 201804)

2016177

汽车盘式制动器蠕动颤振试验与理论分析*

张立军，张频捷，孟德建

(同济大学汽车学院，上海 201804)

进行了盘式制动器蠕动颤振的实车道路试验，理清该现象的发生工况与客观特征。在此基础上，以改进的Karnopp摩擦力模型为基础，建立了1/4车起步颤振机理模型和1/2车“弓状变形效应”影响机理模型，进行蠕动颤振再现与关键因素影响分析。结果表明，除摩擦副动静摩擦因数差之外，悬架系统的变形特性、驱动转矩、制动压力变化和前后轴间制动压力分配等都对制动器蠕动颤振有重要影响。

盘式制动器；蠕动颤振；自激振动；粘滑运动

前言

汽车制动器会产生多种振动和噪声问题，严重损害汽车性能和质量。按频率分，1 000Hz以下主要是制动抖动(brake judder)和制动颤振(brake groan)以及伴生的异常噪声；而在1 000Hz以上则主要是低频和高频制动尖叫(brake squeal)[1]。以往，工业界和学术界重点研究制动抖动和制动尖叫[2-4]，而对制动颤振的关注相对不足。

近年来，随着自动挡汽车的日益普及，汽车制动器的颤振及伴生异响问题日益为广大汽车用户所诟病。根据国际权威第三方评测机构J. D. Power发布的中国汽车市场新车质量报告[5]，2009-2013年制动器振动和噪声问题一直排在前3位。其中，对制动颤振的抱怨和投诉占据主导地位。其原因在于，随着我国汽车保有量的迅猛增长和大中城市交通拥堵的不断加剧，汽车“走走停停”，低速反复起步和制动频发，大大增加了制动器蠕动颤振的发生机率。

长期以来，研究者将蠕动颤振发生机理归结于制动器的粘滑振动激励机制[6-9]和悬架系统的传递方法作用[7，10-12]，因此重点致力于开发具有小动静摩擦因数差的摩擦材料配方[13-15]，和优化具有低振动传递率的悬架系统[10-12]。但迄今为止尚未完全解决问题，也未取得令人完全满意的控制效果。

本文中在试验研究中发现悬架系统存在显著的变形，这在很多前期的研究成果中也有描述[6,7,11,16-17]。但前期研究几乎都忽略了这一极其重要的现象，未将悬架系统的变形纳入制动颤振发生机理的研究中，这必然会导致有关制动颤振发生机理的研究缺乏系统性和全面性。有针对性地开展研究，既有利于深化制动颤振的机理理论，也能够为寻求更广泛和更有效的制动颤振控制措施提供指导。

在此背景下，本文中将针对某自动变速汽车起步时发生的盘式制动器蠕动颤振，通过道路试验详细考察蠕动颤振发生时的振动和悬架变形特征。在此基础上，基于一种新建的、能够再现摩擦力在极低速情况下自平衡特点的改进Karnopp摩擦力模型，分别建立1/4车蠕动颤振机理模型和考虑悬架系统变形的1/2车“弓形效应”机理模型，深入探讨蠕动颤振的发生机理，分析摩擦副特性、动力驱动和悬架系统参数的影响。

1 制动器蠕动颤振的道路试验与分析

1.1 试验工况设置

为深入了解制动器蠕动颤振现象的基本特征，开展表1所示工况下的蠕动颤振道路试验并进行主观评价与客观分析。表中，工况I为参考工况，工况II用以考察制动过程对蠕动颤振的影响，工况III通过增加发动机转速提高了车辆起步时的驱动力矩，用以考察驱动力矩对蠕动颤振的影响，工况IV断开了动力总成，用以考察去除了驱动力矩波动因素以后，蠕动颤振是否依然产生。

表1 试验工况

1.2 主观感受和客观测量结果

(1)工况I 当驾驶员缓慢释放制动踏板即将起步时，制动器发生明显的蠕动颤振和异响，噪声从尖锐的、长间隔的脉冲状异响，逐渐转变为柔和的、短间隔的异响。图1为蠕动颤振发生过程中制动钳的实测垂向加速度，图2为一次冲击的时间展开图。由图1和图2可知，蠕动颤振具有明显的瞬态冲击特征与试验中的主观噪声感受相一致。另外，由于左右制动钳的振动加速度冲击并不完全同步，这说明蠕动颤振与动力系统转矩波动关系不大。

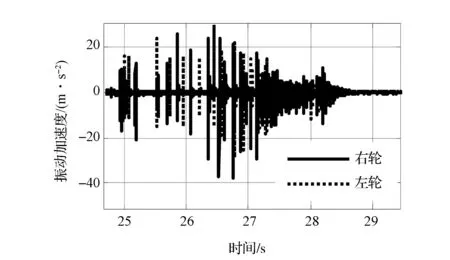
图1 制动钳垂向振动加速度

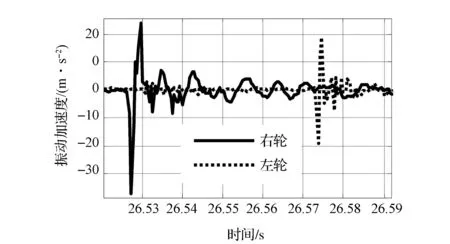
图2 蠕动颤振的一个脉冲

(2)工况II 当驾驶员挂上N挡并释放制动踏板以后，悬架姿态出现明显的变化，前后车轮都会向后滚动一个很小的距离，前后车轮之间的距离比制动释放前增加0.5cm(如图3所示，前轮向后滚动1.8cm，后轮向后滚动2.3cm)。当驾驶员第2次释放制动踏板起步时，出现与工况I中类似的颤振异响，但剧烈程度小于工况I。

图3 释放制动踏板前后轮之间距离的变化

(3)工况III和工况IV 出现与工况I中类似的颤振异响。工况III中，由于提高了发动机转速，车辆起步时的制动力与驱动力都更大，起步蠕动颤振显著加强。个别客户抱怨车辆冷态起步时蠕动颤振现象有所加强，可能就是由于发动机冷起动喷油加浓使发动机怠速转速升高导致的。在工况IV中，虽然坡道产生的驱动力不会产生波动，但蠕动颤振依然存在，并且坡道变陡，蠕动颤振也会显著增强。

1.3 蠕动颤振的主要特征综合分析

综上，汽车起步时的制动器蠕动颤振异响具有如下基本特点：

(1)制动蠕动颤振会在存在驱动力和制动力冲突的情况下发生，与驱动力的来源无关(D挡/R挡发动机驱动，或N挡坡道上重力驱动)；

(2)车辆起步过程中的蠕动颤振异响逐渐由尖锐大周期脉冲演变为柔和小周期脉冲；

(3)起步时的驱动力变大(发动机转矩增大或坡道变陡)，颤振异响会趋于恶化；

(4)车辆在一定的车速制动后，前后轴轴距会微小缩短。通过复原轴距，有助于缓解再次起步时的蠕动颤振异响烈度。

2 制动器蠕动颤振的机理分析

2.1 分析思路

通常认为制动器蠕动颤振主要发生在车辆临界起步阶段，其产生原因为动静摩擦因数之差。因此，首先建立改进的Karnopp摩擦力模型，从而改善模型在极低速情况下对摩擦力的模拟。

然后，针对蠕动颤振的特点(2)和(3)，建立面向1/4车的蠕动颤振机理模型，再现汽车起步时的蠕动颤振振动特征，解释汽车蠕动颤振的发生机理，并着重分析悬架扭曲变形的影响。

最后，考虑制动作用引起的轴距缩短效应，提出所谓“弓形变形效应”概念，建立面向1/2车的蠕动颤振激励机理模型，解释悬架姿态对起步蠕动颤振的影响机制。

2.2 自激振动机理模型

通常，经典的库仑摩擦力模型具有以下特点：(1)当摩擦副存在相对速度Δv时，摩擦因数等于动摩擦因数μd；(2)当摩擦的相对速度为0时，摩擦力自动平衡外力，使得摩擦副相对速度保持为0，但摩擦力不得大于最大静摩擦因数μs与正压力N的乘积。

在实际的数值计算中，不存在相对速度为0的情况。因此，假设当相对速度绝对值小于小量ε时，即认为摩擦副进入锁止状态。为了增强算法的稳定性，当摩擦副进入锁止状态后，增加一个收敛数k，使得进入锁止状态后相对速度能够缓慢回复到0。

如果摩擦副的主动侧与被动侧皆为弹簧质量系统，则摩擦力模型可表示为

(1)

(2)

(3)

2.3 汽车起步的蠕动颤振机理模型

2.3.1 起步颤振机理模型建立

图4为研究自激振动常用的机理模型，该图表明，传送带、质量块和弹簧阻尼系统是自激振动不可或缺的3个要素。在汽车前悬总成上，同样具有这3个要素。

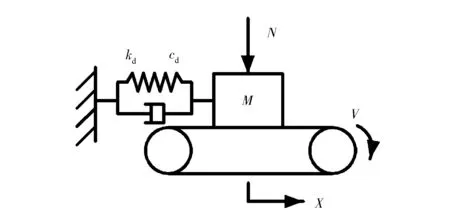
图4 摩擦引起的自激振动机理模型

图5为起步时制动器蠕动颤振的模型示意图。图中，可将制动盘面视为传送带，对于自动变速汽车而言，在起步时制动盘始终会作用有来自于发动机的驱动力矩，制动器可视为质量块，而悬架系统则可视为制动器的弹性支撑系统。当存在制动摩擦力作用时，悬架系统发生如图中虚线所示的弯曲变形，由此会使制动块沿制动盘的周向上产生一个位移，这为制动器的自激振动提供了可能性。

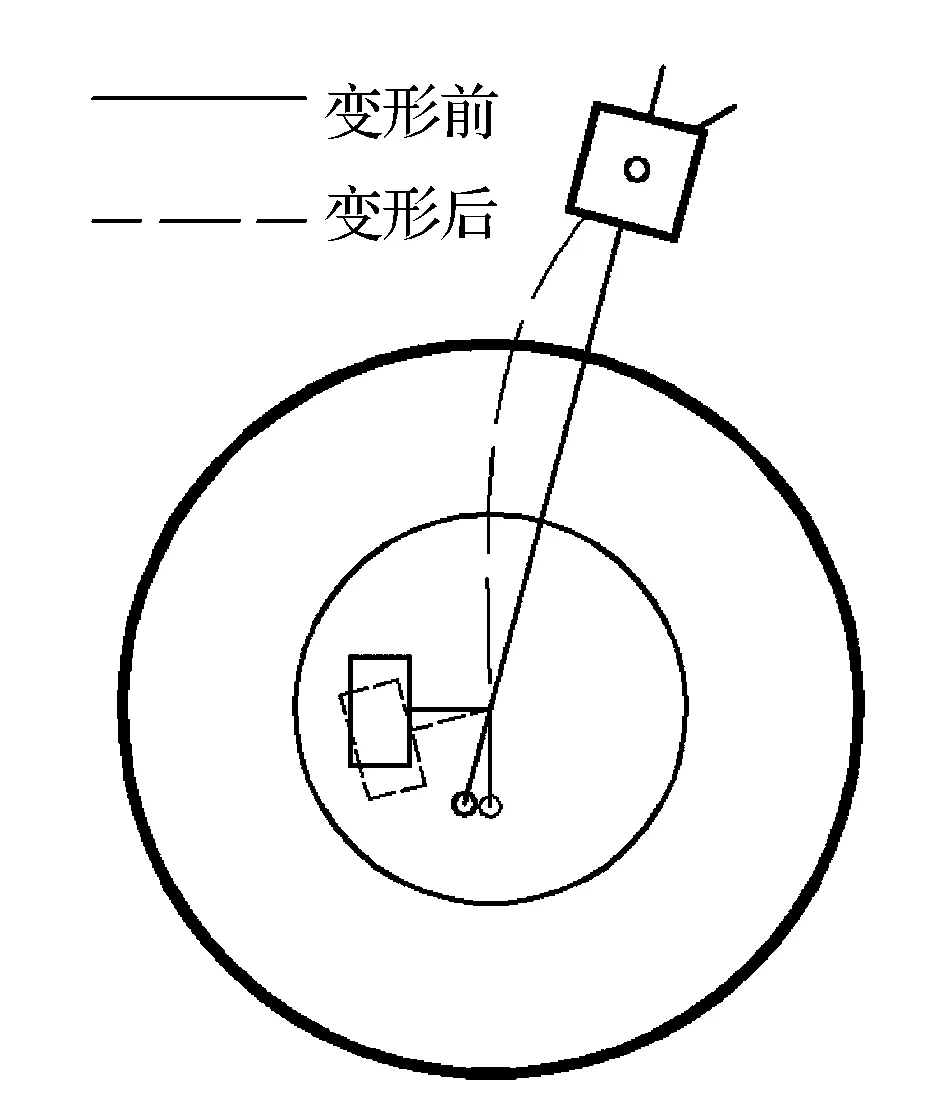
图5 起步蠕动颤振原理

基于以上认识，假设车轮与地面纯滚动并忽略轮胎刚度，建立起步蠕动颤振机理模型，如图6所示。其中，Mb为制动器的质量；Kb和Cb分别为前悬架系统的纵向弯曲刚度与阻尼系数；Md为动力传动系统和制动盘总等效质量；Mv为1/4车辆的等效质量；Kkc和Ckc为悬架纵向的C特性；Fd为作用在制动盘上的驱动力；Nf为制动压力作用；xb，xd和xv分别为制动器、制动盘和车辆的位移。

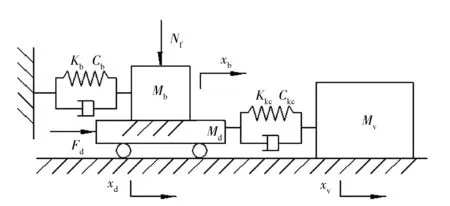
图6 起步颤振机理模型

建立系统的运动学方程为

(4)

式中：fresist为车辆受到的滚动阻力；f为Mb与Md之间的摩擦力，由式(1)～式(3)计算获得。

式(1)中：

(5)

式(3)中：N=Nf

(6)

2.3.2 起步颤振机理与影响因素分析

对模型施加制动压力，如图7所示。先让车辆紧急制动，待车速达到一定数值后，逐渐减小制动压力，使车速慢慢上升，由此再现工况I下的蠕动颤振现象。

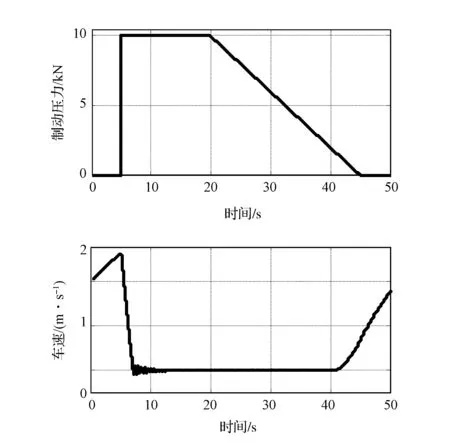
图7 起步蠕动颤振仿真工况

提取汽车起步阶段Mb的振动加速度，如图8所示。显然系统发生了明显的自激振动现象，而且具有先是尖锐大周期脉冲，然后逐渐变化为柔和小周期脉冲的特点，这与试验中观察到的蠕动颤振特征完全一致。同时，每次瞬态波动的信号特征又与图2所测得的制动钳振动加速度信号非常相似。这说明所建立的模型可有效地反映蠕动颤振的根本特征。

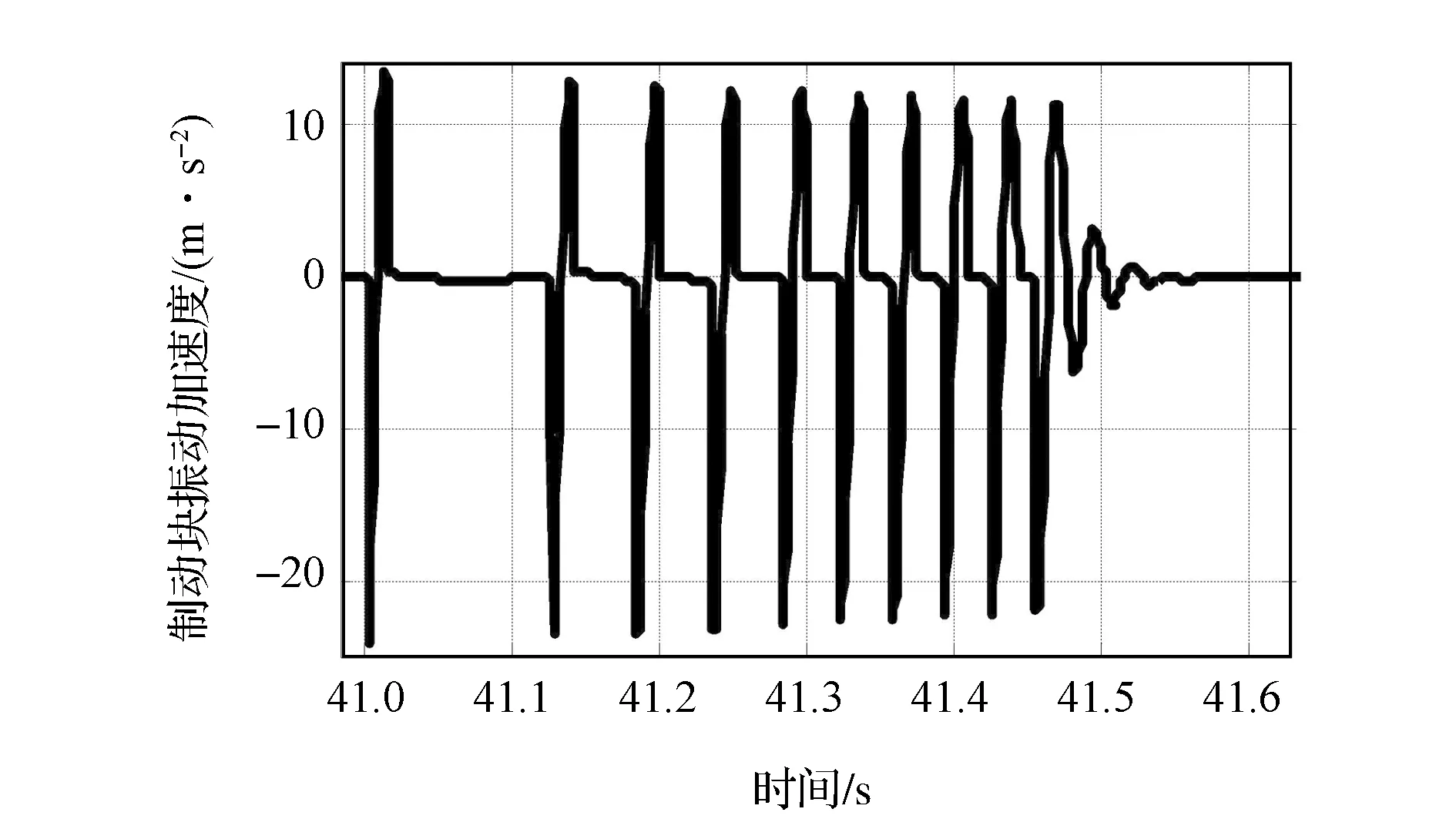
图8 制动块振动加速度

下面通过仿真计算，考察发动机驱动力、悬架系统参数和制动器参数的影响。

(1)发动机驱动力大小的影响

将发动机驱动力Fd放大1.5倍(从720变为1 080N)，仿真结果如图9所示。由于驱动力的增大改变了与制动力平衡的临界点，颤振现象被提早触发，并且颤振的振动强度有所加大。这与试验工况III中观察到的试验结果一致。

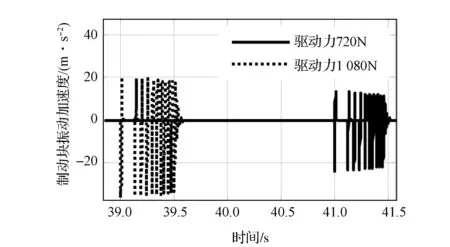
图9 驱动力对起步蠕动颤振的影响

(2)悬架和制动器系统参数的影响

分别将悬架弯曲刚度Kb、制动器质量Mb和悬架C特性Kkc加倍，分析其对制动块振动加速度的影响，仿真结果如图10～图12所示。

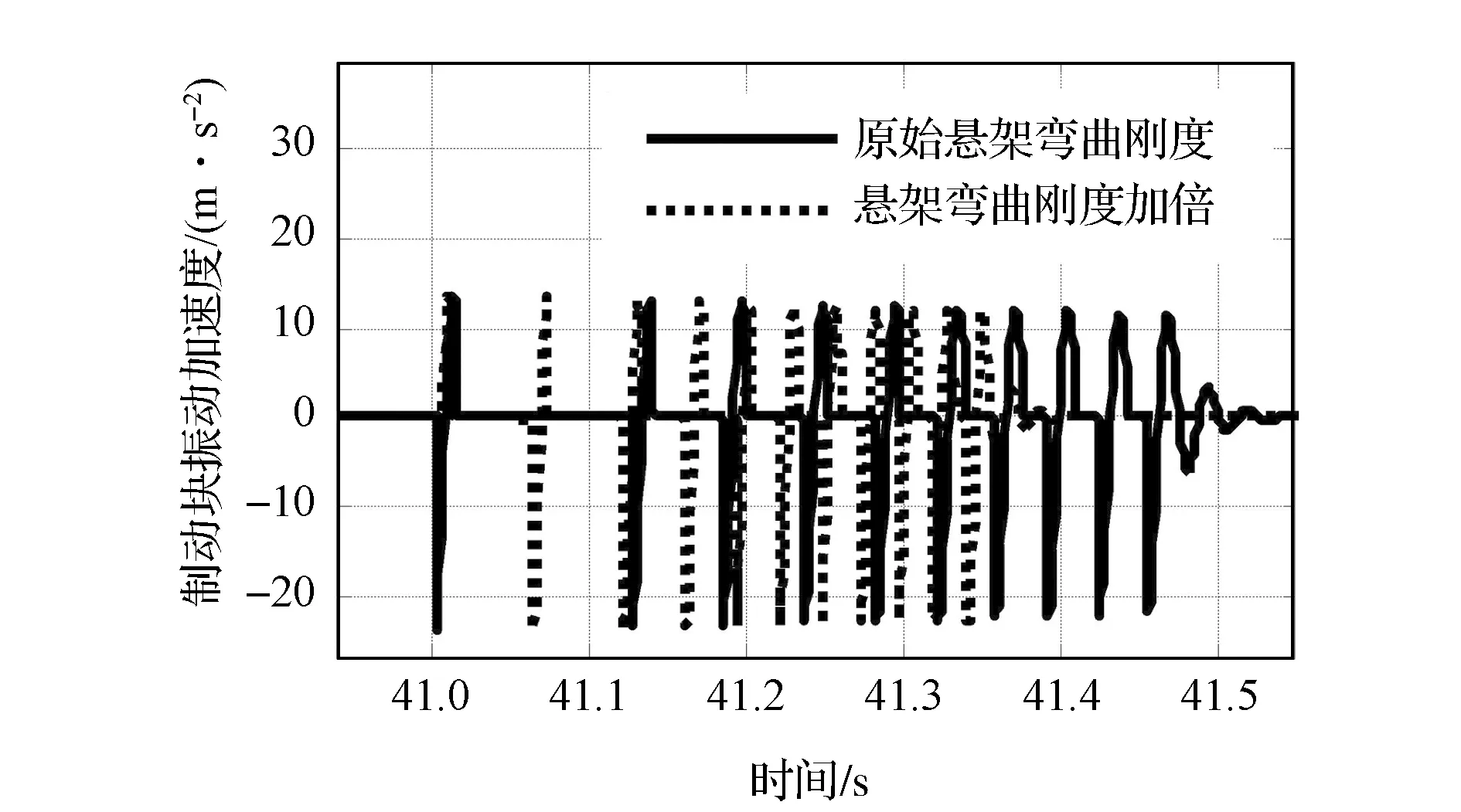
图10 悬架弯曲刚度对起步蠕动颤振的影响

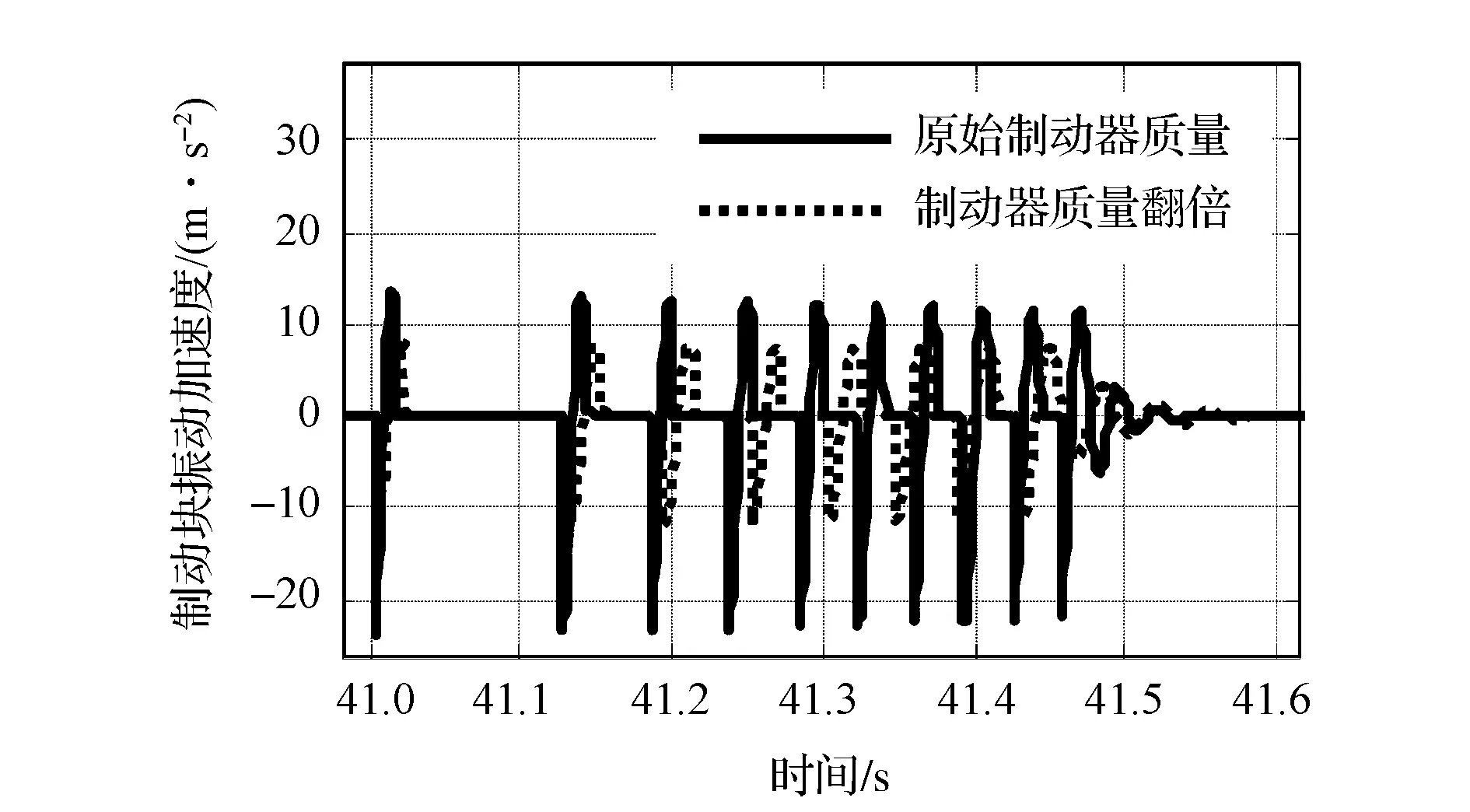
图11 制动器质量对起步蠕动颤振的影响

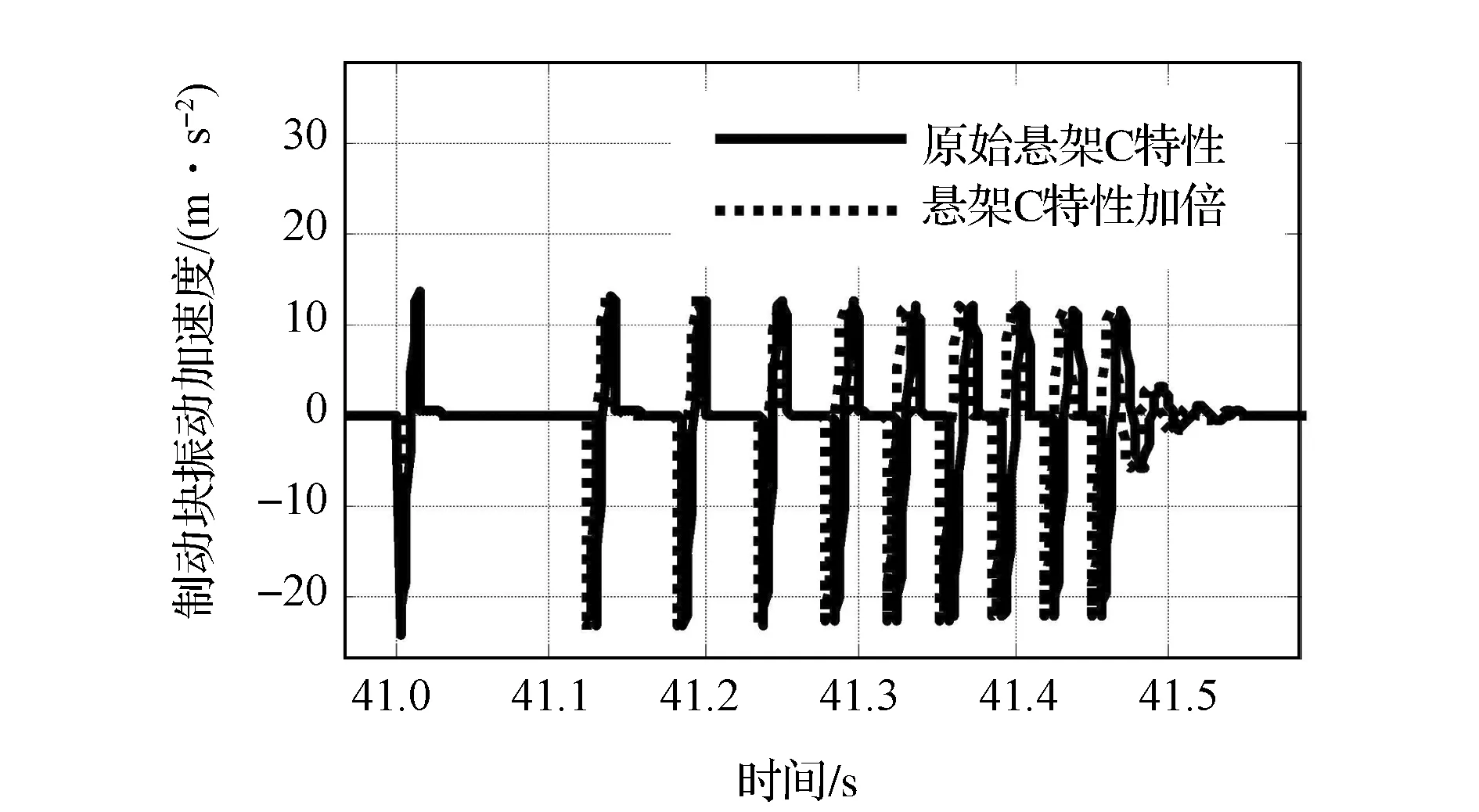
图12 悬架C特性对起步蠕动颤振的影响

仿真结果表明，增加悬架系统的弯曲刚度不会减小颤振的振动强度，但可以缩短颤振的持续时间；制动器质量的变化对颤振强度的影响很显著，增大制动器质量可有效减小颤振强度；悬架纵向弹性运动学特性的影响在该模型中无法反映出来。

2.4 汽车起步的弓形效应蠕动颤振机理模型

2.4.1 弓形效应机理模型建立

2.3节中的模型仍然存在明显的局限性。当车辆处于静止状态时，车轮不受路面切向力与滚动阻力作用，因此车轮仅受到制动块摩擦力与传动系统的驱动力作用，模型的边界条件仅与发动机的驱动力矩有关，这就无法解释1.2节中起步蠕动颤振的特点(4)。

实际车辆在制动过程中，前后车轮受到的法向力与纵向力会发生变化，由于悬架的K&C特性影响，轴距会缩短，如图13中虚线所示。由于车辆存在一个类似绷紧弓的变形，本文中将其命名为“弓形效应”。

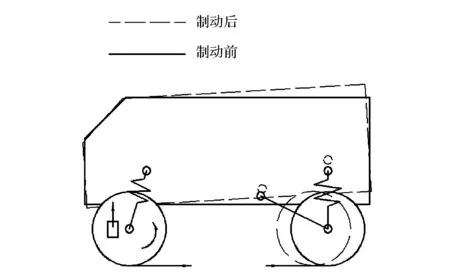
图13 弓形效应原理

如果车辆制动停车后释放制动，前后车轮受到的法向力与纵向力会恢复到原始状态，轴距也会恢复，弓形变形消失。但是，如果制动停车后驾驶员没有松开制动踏板，制动器的制动作用会阻止车轮的滚动恢复，弓形效应保持，轴距不能恢复。此时，前后车轮之间就会产生一对大小相等，方向相反的作用力。

这对力会引起制动力边界条件的改变。如图13中所示的前轮的受力分析，前轮上的制动器制动力矩、驱动力矩与路面纵向力平衡。而且，路面纵向力越大，制动力也越大，相当于增加了图6所示模型的驱动力Fd，所以颤振异响将会加剧。

在城市行驶工况中，由于需要频繁起停车辆，所以经常出现挂在D挡不松制动踏板的停车工况，因此由于弓形效应引起的起步蠕动颤振加剧的情况也必将经常出现。

根据上述分析，建立弓形效应机理模型，如图14所示。左半部分表示车辆前轴，右半部分表示车辆后轴。驱动力Fd只单独作用于前轴上，制动力通过制动力分配系数β分配在前后轴制动器上，产生Nf和Nr两个制动压力，并且有

(7)

式中Nsum为前后总制动压力。

运动学方程为

(8)

式中：ff和fr都可由式(1)～式(3)计算获得，具体计算方法与式(5)和式(6)相似。

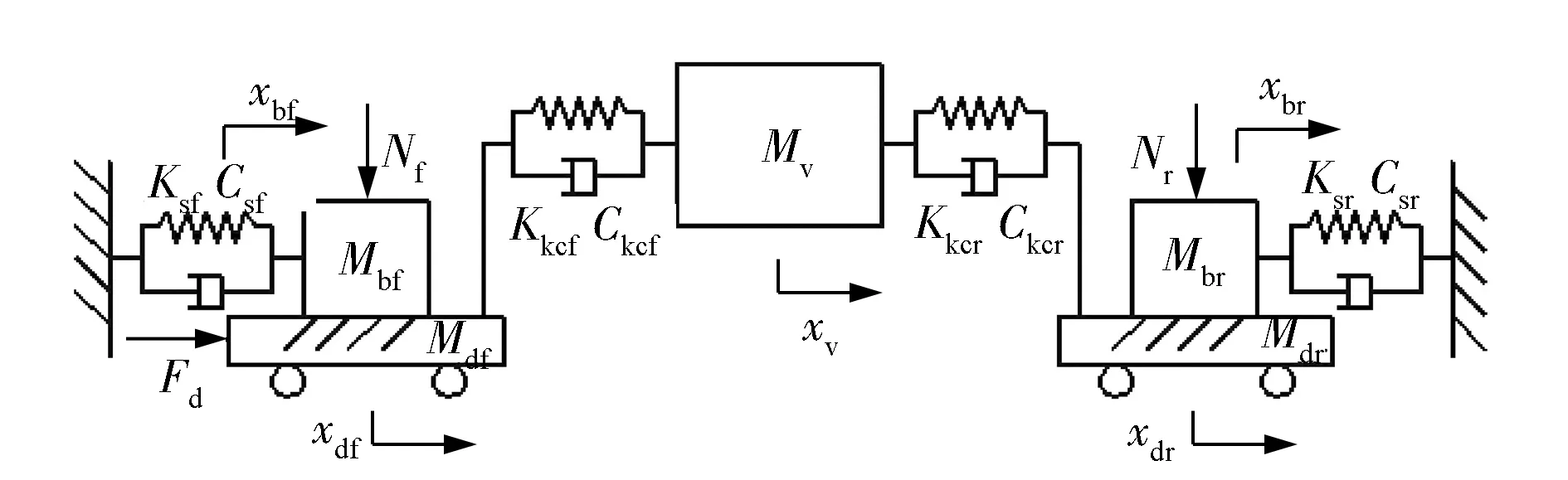
图14 弓形效应机理模型

2.4.2 关键影响因素分析

为了能够再现表1中工况II对应的现象，定义模型的输入信号不仅包括前后轴总制动压力Nsum，还包括驱动力挡位P，并有

Fd=P·Fe

(9)

式中Fe为发动机实际输出的驱动力。显然，当P=1时，传动系统处于D挡，当P=0时，传动系统处于N挡。

根据表1中工况I和工况II，对仿真模型输入如图15所示的输入量，图15(a)对应工况I，为一般制动工况，图15(b)对应工况II，为释放弓形效应的工况。

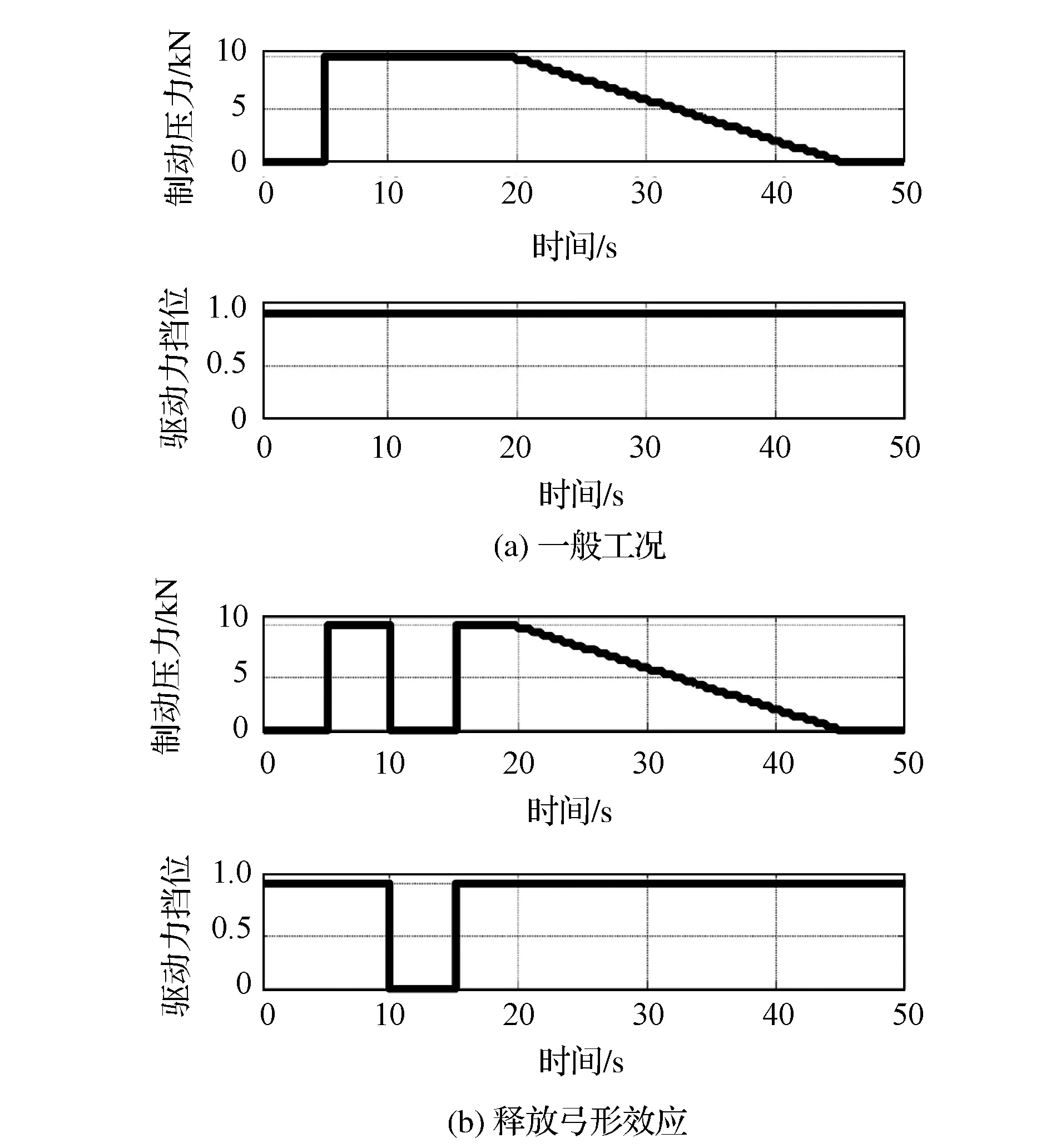
图15 弓形效应仿真工况

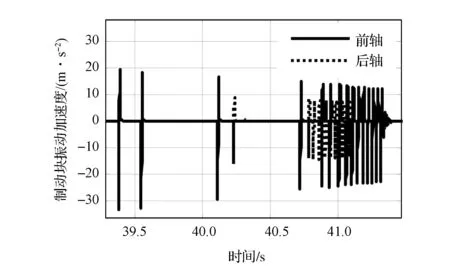
图16 前后制动块的振动加速度

图16为图15(a)输入量对应的仿真结果。对比图8可以发现，引入了1/2车模型及悬架弓形效应以后，起步蠕动颤振现象，尤其是前轴的起步蠕动颤振振动发生了巨大改变，在连续的起步蠕动颤振发生前，会出现几次间断的，更加剧烈的颤振脉冲。很明显，这些脉冲会大大降低制动系统NVH性能，同时驾驶员的主观感受势必也会大幅降低。

图17为一般工况与释放弓形效应工况之间的仿真对比结果。由图可见，释放弓形效应以后，前后车轴起步蠕动颤振异响都得到了明显的改善。这与1.2节中起步蠕动颤振的特点(4)一致，也很好地说明了悬架的弓形效应对汽车起步蠕动颤振有重要的影响。

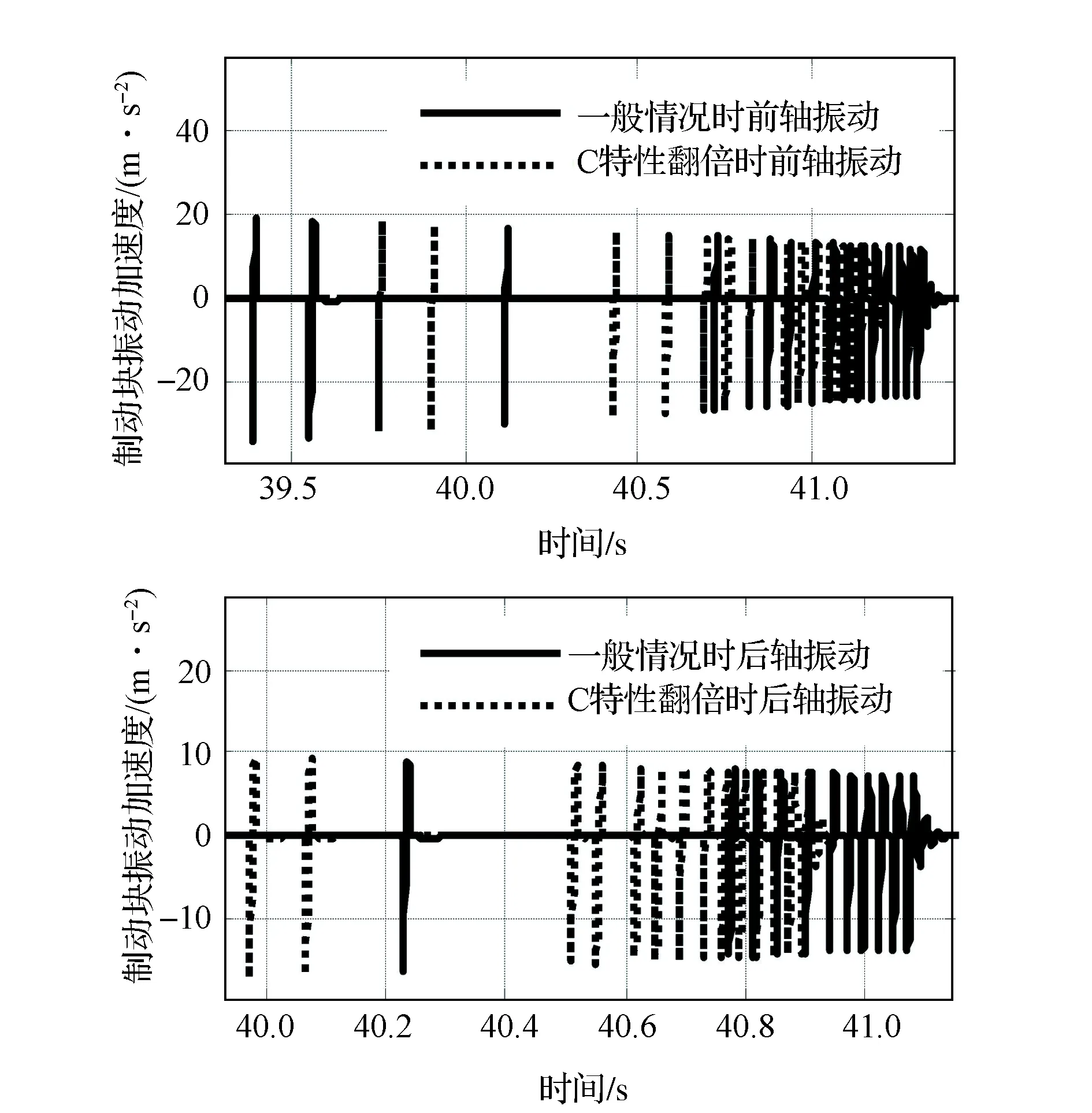
图18 悬架C特性对起步蠕动颤振的影响

图18为不同悬架C特性对起步蠕动颤振的影响。虽然悬架C特性引起的弓形效应对起步蠕动颤振影响显著，但是其C特性的大小本身对起步蠕动颤振影响不大。悬架C特性的大小会影响到弓形效应引起的轴距缩短量，但是前后轮之间力的大小却主要是由制动减速度大小决定的。

制动力分配系数也是制动系统的重要参数，如果路面纵向力引起的前后悬架纵向变形完全相同，则弓形效应也会消失。图19为制动力分配系数β等于0.75，0.5和0.25 3种情况下的起步蠕动颤振现象。图19(a)采用的仍是一般工况，可以明显发现，随着β的变小，前轴颤振异响逐渐削弱，后轴颤振异响逐渐加强，其中，当β=0.5时，前轴颤振异响持续的时间最短，说明改变制动力分配系数的确起到了减小弓形效应的作用。为了消除弓形效应的影响，单纯从制动力大小的角度分析其对颤振异响的影响，图19(b)对比了3种制动力分配系数下释放弓形效应工况时的颤振异响，发现无论是前轴还是后轴，颤振异响的剧烈程度会随制动力的降低而降低。然而，由于后轴颤振异响本身不太明显，且后轴振动到车内噪声的传递函数较小，以牺牲后轴颤振异响为代价，减小前轴颤振异响的大小，对于降低车内异响的主观感受有一定帮助作用。

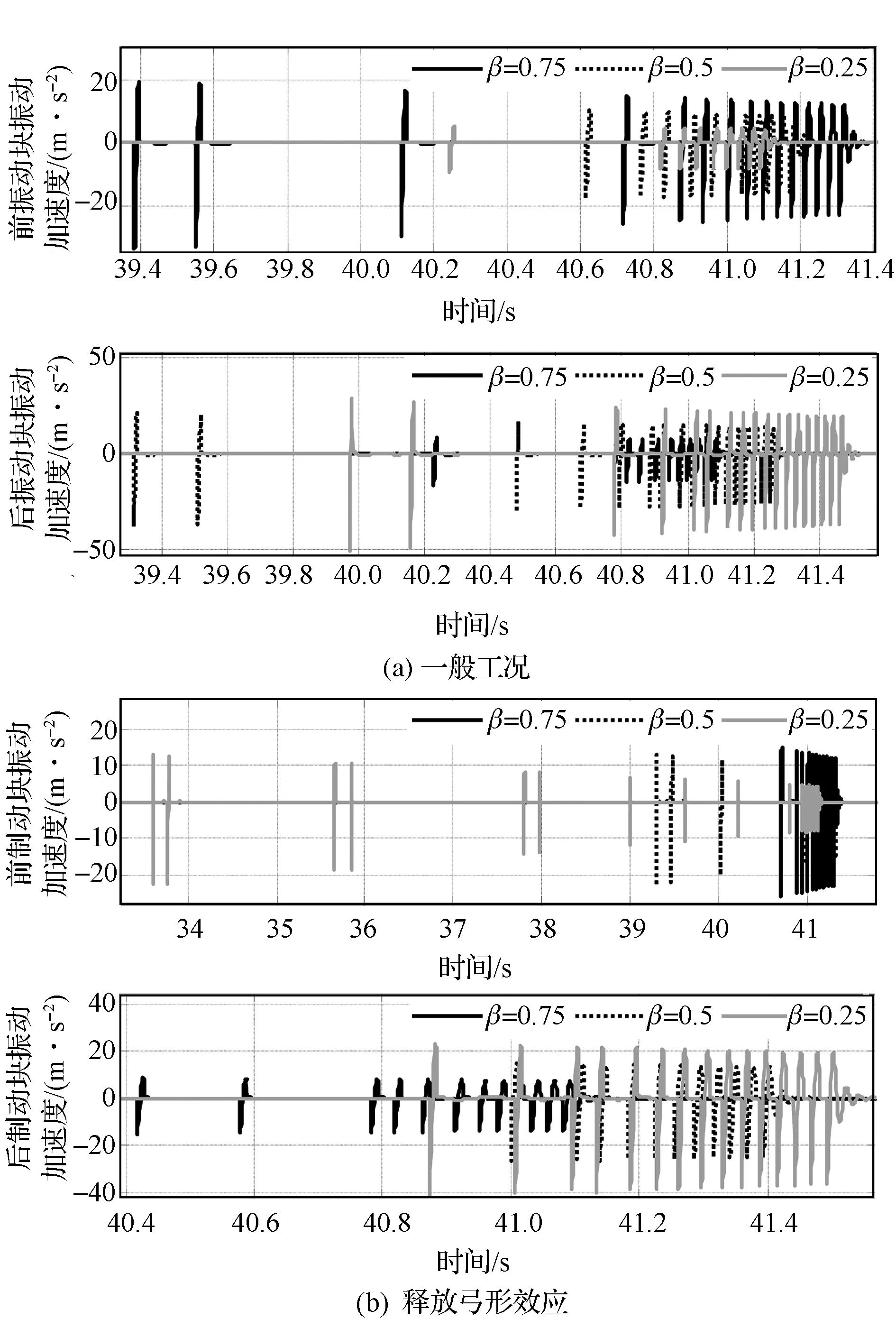
图19 制动力分配对起步蠕动颤振的影响

3 结论

(1)进行了汽车起步蠕动颤振主观评价试验，获得了汽车起步蠕动颤振的几个主要特征，并建立相关理论模型解释了其特征产生的原因。

(2)建立了改进的Karnopp摩擦力仿真模型，从而实现了对汽车极低速临界起步阶段颤振异响问题的仿真。

(3)建立了起步蠕动颤振机理模型，证明了驱动力大小与悬架振动特性对于起步蠕动颤振具有一定的影响。

(4)提出弓形效应理论，建立了弓形效应机理模型，证明了弓形效应对于起步蠕动颤振具有一定的影响，并发现制动力分配系数对于起步蠕动颤振现象具有显著的影响。

[1]LIUWeiming,PFEIFERJeromeL.Introductiontobrakenoise&vibration[EB/OL].www.sae.org/events/bce/honeywell-liu.pdf, 2010.

[2]JACOBSSONH.Aspectsofdiscbrakejudder[J].ProceedingsoftheInstitutionofMechanicalEngineers,PartD:JournalofAutomobileEngineering, 2003, 217(6): 419-430.

[3]KINKAIDNM,O’REILLYOM,PAPADOPOULOSP.Automotivediscbrakesqueal[J].JournalofSoundandVibration, 2003, 267 (1): 105-166.

[4] 张立军，刁坤. 摩擦引起的振动噪声文献综述与研究展望[J].同济大学学报，2013,41(5):765-772.

[5]J.D.Power亚太公司. 中国新车质量研究[EB/OL]，www.jdpowerchina.com.cn, 2013-10-31.

[6]ABDELHAMIDMohamedKhalid.Creepgroanofdiscbrakes[C].SAEPaper951282.

[7]BRECHTJörg,HOFFRICHTERWolfgang,DOHLEAchim.Mechanismsofbrakecreepgroan[C].SAEPaper973026.

[8]CROWTHERAshleyR，YOONJ,SINGHR.Anexplanationforbrakegroanbasedoncoupledbrake-drivelinesystemanalysis[C].SAEPaper2007-01-2260.

[9]WUGuangqiang,JINShuyi.Combinationoftestwithsimulationanalysisofbrakegroanphenomenon[C].SAEPaper2014-01-0869.

[10]YOONKyuWon,LEEJaeCheol,CHOSungSun.Thestudyofvehiclestructuralcharacteristicsforcreepgroannoise[C].SAEPaper2011-01-2363.

[11]JUNGTaeho，CHUNGSeung.Researchforbrakecreepgroannoisewithdynamometer[C].SAEPaper2012-01-1824.

[12]JOOKyungHoon,JEONHyunCheol,SUNGWeonchan,etal.Transferpathanalysisofbrakecreepnoise[C].SAEPaper2013-01-2036.

[13]FUADIZahrul,ADACHIKoshi,IKEDAHideaki,etal.Effectofcontactstiffnessoncreep-groanoccurrenceonasimplecaliper-sliderexperimentalmodel[J].TribologyLetters,2009, 33(3):169-178.

[14]OKAYAMAK,FUJIKAWAH,KUBOTAT,etal.AStudyonreardiscbrakegroannoiseimmediatelyafterstopping[J].SAEPaper2005-01-3917.

[15]JANGH,LEEJS,FASHJW.Compositionaleffectsofthebrakefrictionmaterialoncreepgroanphenomena[J].Wear, 2001, 251(1): 1477-1483.

[16]DUNLAPKBrent,RIEHLEMichaelA,LONGHOUSERichardE.Aninvestigativeoverviewofautomotivediscbrakenoise[C].SAEPaper1999-01-0142.

[17]VADARIVish,JACKSONMark.Anexperimentalinvestigationofdiskbrakecreep-groaninvehiclesandbrakedynamometercorrelation[C].SAEPaper1999-01-3408.

Tests and Theoretical Analysis of Creep Groan in Vehicle Disc Brake

Zhang Lijun，Zhang Pinjie & Meng Dejian

CollegeofAutomotiveStudies，TongjiUniversity，Shanghai201804

A real vehicle test is conducted on the creep groan of disk brake to clarify the occurring conditions and objective features of that phenomenon. On this basis, a 1/4 vehicle model for creep groan mechanism in vehicle start up and a 1/2 vehicle model for the affecting mechanism of ‘bow-shaped deformation effects’ are created, based on the improved Karnopp friction model, to reproduce creep groan and analyze the effects of key factors. The results show that the deformation characteristics of suspension, driving torque, braking pressure and the braking force distribution between axles also have important effects on the creep groan of disk brake, besides the difference between static and kinetic friction factors.

disk brake; creep groan; self-excited vibration; stick-slip motion

*国家自然科学基金(51575395)资助。

原稿收到日期为2015年6月18日，修改稿收到日期为2015年9月1日。