基于组合代理模型的车身多学科设计优化*

黄焕军,张博文，吴光强,2,李 凡

(1.同济大学汽车学院,上海 201804； 2.东京大学生产技术研究所,东京 153-8505)

2016173

基于组合代理模型的车身多学科设计优化*

黄焕军1,张博文1，吴光强1,2,李 凡1

(1.同济大学汽车学院,上海 201804； 2.东京大学生产技术研究所,东京 153-8505)

本文对比分析了4种单一代理模型和两种组合代理模型的预测能力，并基于各代理模型进行正面碰撞安全性多目标优化，结果发现，组合代理模型不仅具有较好的预测精度和稳健性，还能促进最优解的搜索。基于上述分析，采用组合代理模型拟合正面碰撞、侧面碰撞和白车身模态分析的各种响应，建立针对安全性的车身结构多学科优化模型，并用协同优化方法求解。结果表明：组合代理模型在多目标优化中有利于得到更满意的最优解；基于组合代理模型的车身结构多学科设计优化有效改善了汽车的碰撞安全性，并兼顾了轻量化和NVH性能。

车身；组合代理模型；碰撞安全性；多学科优化；协同优化

前言

伴随着汽车的发展，道路交通事故日趋频繁，碰撞安全作为汽车安全性的重要环节受到广泛关注。而车身是碰撞中最主要的吸能元件，因此研究车身结构具有重要的意义。汽车车身结构是一个复杂的系统，除碰撞安全性外，还要满足NVH性能、结构强度、刚度和轻量化等要求，涉及多种学科。同时，各学科高度关联、相互耦合[1]，使得传统的串行设计方法很难得到全局最优解[2]。采用多学科设计优化(multidisciplinary design optimization, MDO)理论可以综合考虑多个学科对汽车整体性能的影响。近10年来MDO的应用已不再局限于航空航天领域，许多学者开始进行MDO在汽车领域中应用的研究[1-4]。

车身结构优化通常基于有限元方法，这需要耗费巨大的计算资源。解决上述问题的一个有效方法就是采用代理模型，最优解很大程度上取决于代理模型的精度和特性[5]。目前，车身结构MDO中使用的代理模型包括多项式响应面[1](polynomial response surface, PRS)、径向基函数神经网络[6](radial basis function, RBF)、克里金[7](Kriging, KRG)和支持向量回归[8](support vector regression, SVR)模型等。针对不同的优化问题，上述单一代理模型表现各异，采用组合代理模型[9-10]可综合各个单一代理模型的优势，适应不同类型的问题，但将组合代理模型用于车身结构多学科优化的研究很少。

本文中首先对比分析了组合代理模型与各单一代理模型的预测能力，以及在汽车正面100%刚性壁碰撞(简称“正面碰撞”)优化中的应用效果，验证了组合代理模型的优越性。然后，针对正面碰撞、侧面碰撞和白车身模态子系统，采用协同优化方法进行车身结构碰撞安全性多学科设计优化。

1 代理模型的相关理论

1.1 多项式响应面

多项式响应面是一种数理统计技术，最常用的是二次多项式响应面模型，其表达式为

(1)

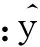
1.2 径向基函数神经网络

径向基函数神经网络是一种利用离散数据拟合多元函数的方法。它以径向函数为基函数，通过线性叠加构造而成，其基本形式为

(2)

式中：ri=‖x-xi‖为欧几里德距离，即x与第i个样本点xi在设计空间上的距离；λi为基函数的加权系数；n为基函数的个数；φ为基函数，常见类型包括高斯函数、多二次函数、逆多二次函数和薄板样条函数等。

1.3 克里金

克里金是一种估计方差最小的无偏估计模型。它具有局部估计的特点，包含了回归部分和非参数部分，具有如下形式：

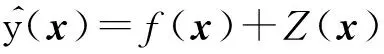
(3)

式中：f(x)为x的已知函数，可以是常数、一次或二次多项式；Z(x)为均值为0、方差为σ2的随机误差。Z(x)的协方差为

(4)

式中：dk=|xik-xjk|为训练样本点xi和xj第k个分量的距离；n为设计变量个数；Rk(dk)为相关函数，常用的有线性函数、三次函数、样条函数、球函数、指数函数、幂函数和高斯函数等。

1.4 支持向量回归

支持向量回归是一种基于支持向量机的响应面模型，其一般表达式为

(5)

式中：αi和αi*为拉格朗日乘子；n为支持向量个数；b为常数项；K(xi,x)为核函数，常见的核函数有线性核函数、多项式核函数、高斯径向基核函数和指数径向基核函数等。

1.5 代理模型内在参数设置

代理模型的内在参数会对其预测精度产生影响，为消除此影响，各代理模型的内在参数统一按表1进行选择。

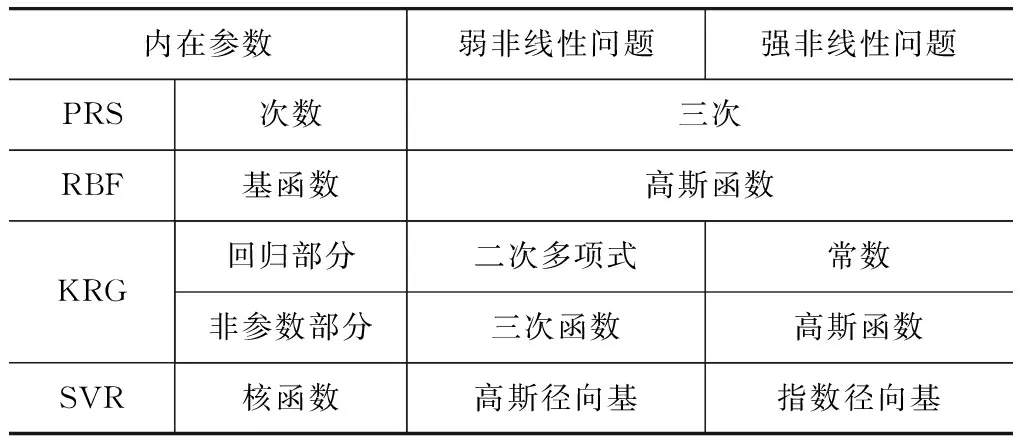
表1 代理模型的内在参数

1.6 误差分析指标

最常用的代理模型误差分析指标是决定系数(coefficient of determination)R2，表达式为

(6)

2 组合代理模型

组合代理模型(ensembleofsurrogates)，又称加权平均代理模型(weightedaveragesurrogates)，其一般形式为

(7)

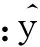
2.1 权系数计算

为使组合代理模型有尽可能高的预测精度，需要确定各权系数。通常，精度高的代理模型选择大的权系数，反之亦然。考虑到实际复杂工程问题的计算时间成本，本文中基于广义均方误差(generalized mean square error, GMSE)开展权系数的研究，可避免使用额外的测试样本。采用留一法(leave-one-out, LOO)得到的交叉验证广义均方误差为

(8)

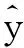
目前，基于GMSE的权系数计算方法有如下两种。

(1)启发式计算方法[9]

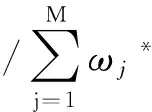
(9)

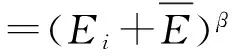
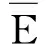
(2)GMSE最小化方法[10]

此方法将权系数的计算过程转化为优化过程，对应的优化问题可表述为

(10)

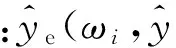
上述两种方法得到的组合近似模型分别表示为EG和EA。

2.2 预测能力分析

为考虑不同的函数维数和响应非线性程度，本文中选取4个典型测试函数来对比组合代理模型与单一代理模型的预测能力。测试函数特征和试验设计(designofexperiment,DOE)设置如表2所示，训练样本和测试样本均采用拉丁超立方方法抽取。

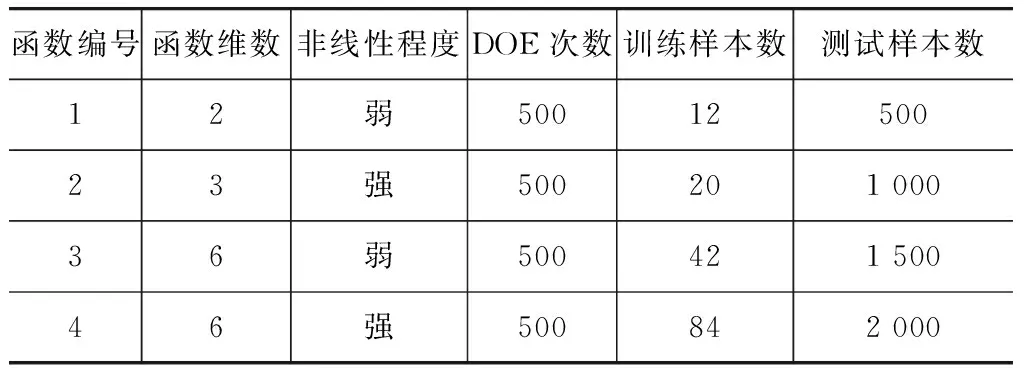
表2 测试函数特征及试验设计设置

(1) 测试函数1(Branin-Hoo)

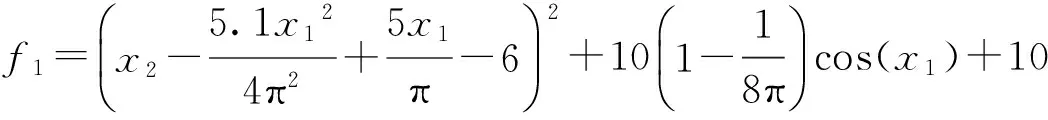
-5≤x1≤10,0≤x2≤15

(11)

(2) 测试函数2(Hartman-3)

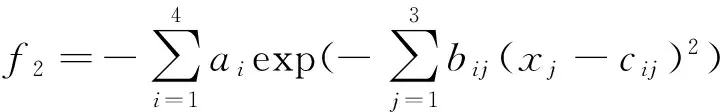
0≤xj≤1

(12)

(3) 测试函数3(ExtendedRosenbrock)

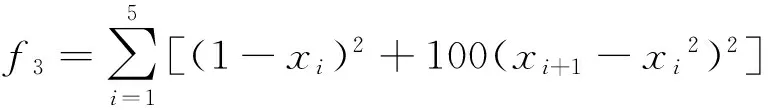
-5≤xi≤10

(13)

(4) 测试函数4(Hartman-6)

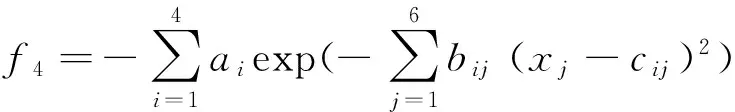
0≤xj≤1

(14)

针对误差分析指标R2，对500次DOE对应的代理模型预测精度进行分析。R2的箱线图如图1所示，图中矩形盒越短，表明预测精度对试验设计的依赖性越小，中位线高度可以大致反映平均预测精度；R2的均值和标准差如表3所示。

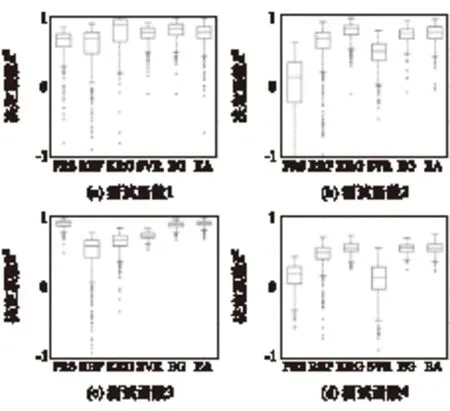
图1 各代理模型R2的箱线图

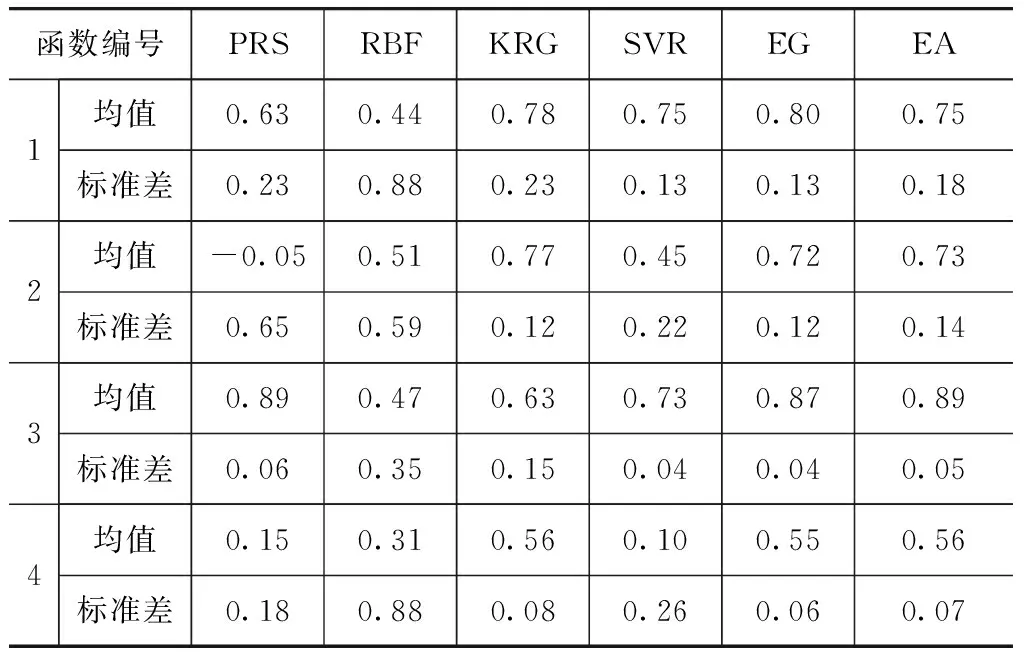
函数编号PRSRBFKRGSVREGEA1均值0.630.440.780.750.800.75标准差0.230.880.230.130.130.182均值-0.050.510.770.450.720.73标准差0.650.590.120.220.120.143均值0.890.470.630.730.870.89标准差0.060.350.150.040.040.054均值0.150.310.560.100.550.56标准差0.180.880.080.260.060.07

由图1可见：PRS在非线性较弱的函数中具有较好的预测能力，在测试函数3中最好，箱线图中表现为矩形盒长度较短且中位线较高，但是非线性程度强时，其预测能力明显下降；RBF对函数非线性的依赖程度要低于PRS，但是其异常值尾线长度最长，稳健性差；KRG的预测精度在大多情况下都优于其他单一代理模型，特别在两个非线性较强的函数中，其中位线最高，矩形盒最短；SVR在测试函数1中预测精度和稳健性最好，在测试函数2中最差。

总体而言，单一代理模型对不同测试函数的预测精度有较大差异，并且依赖于试验设计，表3的数据进一步证实了上述结论。组合代理模型很好地避免了上述两个缺点，EG和EA对各函数都有最好或接近最好的预测精度，且数据分布密集，异常值尾线短，稳健性好。结合表3可知，与EG相比，EA的R2均值大，标准差也大，表明其平均预测精度较高，而稳健性略差一些。

3 汽车正面碰撞多目标优化

3.1 整车正面碰撞仿真分析

按照US-NCAP法规的要求，使汽车以56km/h的速度撞击刚性墙，仿真模型如图2所示，该模型已经由试验验证[11]。利用LS-DYNA进行碰撞仿真，仿真时间为100ms。

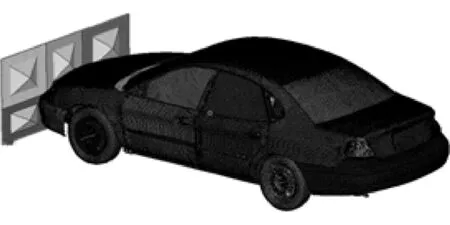
图2 整车正面碰撞有限元模型

B柱加速度峰值aB和踏板位置前围板最大侵入量(简称“前围板最大侵入量”)In可认为是正面碰撞的主要性能指标，其大小直接影响碰撞中乘员的安全。该车的B柱加速度峰值aB=37.7g，前围板最大侵入量In=205.1mm。

3.2 确定优化问题

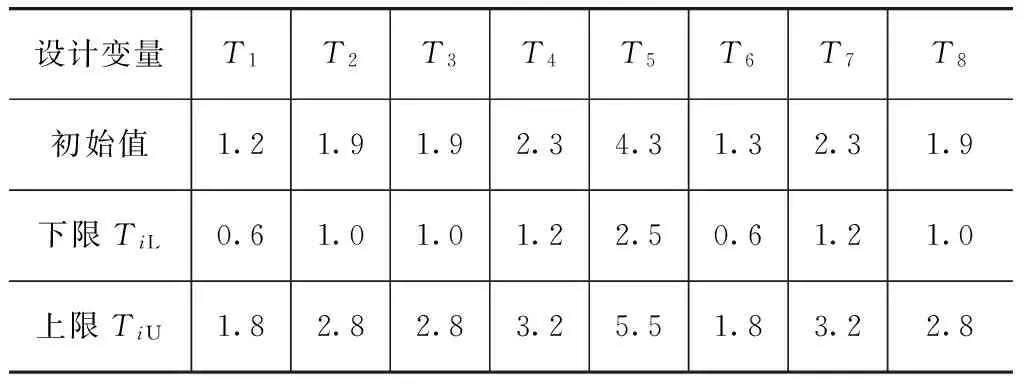
图3 设计变量示意图

本文中依据正面碰撞过程中变形与吸能最大的原则，结合各个部件的质量，最终选取车身前部的12个部件的8组板料厚度作为设计变量[12]，如图3所示。各设计变量的初始值和上下限值如表4所示。选取部件总质量m，B柱加速度峰值aB和前围板最大侵入量In作为响应量。为提高正面碰撞性能并兼顾轻量化，以aB和In最小化为优化目标，以零件质量m不超过56kg为约束，确定正面碰撞多目标优化设计的数学模型为

(15)

3.3 优化问题求解

本文中选用运算速度快、收敛性好的非劣排序遗传算法(NSGA-II)来求解正面碰撞多目标优化问题。优化流程为：采用最优拉丁超立方试验设计方法产生80个训练样本，通过仿真得到对应的响应值；依次构建各种单一和组合代理模型来拟合aB和In，运用1阶多项式准确拟合m；基于代理模型进行优化，得到Pareto前沿。

3.4 优化结果对比分析

为评价各代理模型在正面碰撞多目标优化中的效果好坏，选取Pareto前沿中几个最优解为代表进行对比。显然，选取不同最优解进行对比可能会得到不同的结果。为避免上述情况，对于各代理模型得到的Pareto前沿，本文中均按照权重和妥协方法[13]挑选代表性最优解，分别记作最优解1和最优解2。目标aB和In的加权系数分别取6和1。

最优解1和最优解2处的各代理模型预测值和实际仿真值如表5所示。

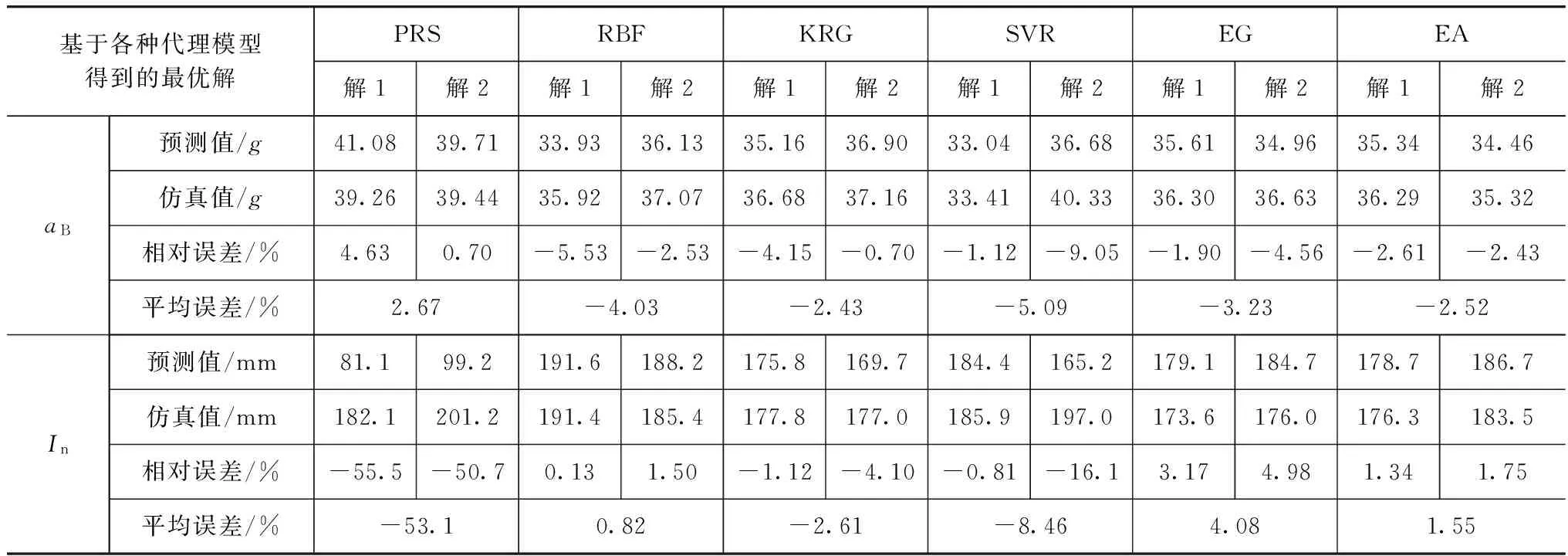
表5 代理模型效果对比

由表可见：RBF和KRG在最优解处精度较高；PRS对In的预测精度非常低，相对误差达到50%以上，这是因为In的非线性程度很高；SVR在最优解1和2处的误差相差较大；基于组合代理模型得到的最优解处误差比较小，尤其是EA，对aB和In都能很准确地预测，平均误差分别为-2.52%和1.55%，且在两个最优点处的表现比较接近，综合性能最好。对比2.2节的结论表明，基于代理模型得到的Pareto前沿和实际点的误差，与代理模型本身的精度有一定的相关性。

从优化效果角度分析，各最优解2对应的妥协方法评价指标(距离d)如表6所示。如果以此作为评价标准，则基于EA得到的最优解2是最满意的，其对应的距离d小于其他方法，基于EG，KRG和RBF的优化效果略差一些。该最满意解对应的B柱加速度峰值为35.32g，前围板最大侵入量为183.5mm，比初始值分别减小了6.31%和10.53%。

表6 妥协方法评价指标

因此，EA不仅具有较好的预测精度和稳健性，而且基于EA进行多目标优化能得到更满意的最优解。

4 车身结构多学科优化

4.1 多学科优化模型

根据多学科设计优化要求，为寻找车身的整体最优性能，需要对影响车身性能的多个子系统进行研究。安全性方面，除正面碰撞外，侧面碰撞也是交通事故的常见形式，且容易造成死亡和重伤。随着人们生活水平的提高，汽车乘坐舒适性亦日渐重要。白车身模态分析作为整车NVH分析中非常重要的一部分，可以反映车身结构的固有频率及振型，以便尽早改进结构，避免共振。因此，本文中建立一个针对安全性的，包含正面碰撞、侧面碰撞和白车身模态等3个子系统的车身结构多学科优化模型。模型框架、各学科设计变量个数及学科间变量耦合关系如图4所示。侧面碰撞子系统选择部件总质量m′和B柱最大侵入量In′作为响应量；白车身模态子系统则选择部件总质量m″和1阶模态频率f为响应量。

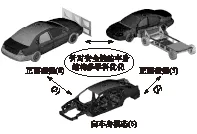
图4 设计变量个数及其耦合关系

4.2 近似模型

侧面碰撞和白车身模态子系统采用最优拉丁超立方方法分别产生50和30个样本点，质量响应均用1阶多项式拟合，其余响应量用EA拟合，表达式为

(16)

4.3 协同优化方法

协同优化是一种两级优化算法，将原有的设计优化问题分为一个系统级优化和多个学科级优化，从而实现学科间的并行计算，可有效解决大规模复杂工程多学科优化问题。

本文中采取协同优化方法求解多学科优化模型，框架如图5所示。

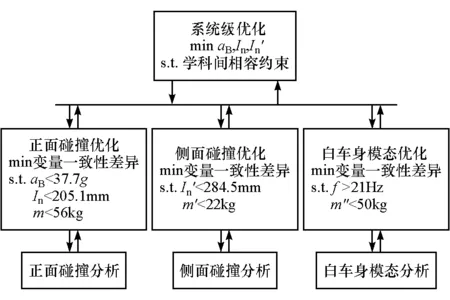
图5 协同优化方法框架

以碰撞安全性的指标aB，In和In′为系统级目标，各设计响应量范围通过学科级约束进行限制。

4.4 优化结果分析

三目标MDO问题的Pareto前沿如图6所示。

图6 三目标Pareto前沿

由图可见，3个目标互相冲突，不可能同时达到最优，且各个最优解之间无法比较。因此，本文中根据设计需要，从Pareto前沿中选择Q点为最满意的最优解。将其对应的设计变量代入各子系统仿真模型，得到各响应量的仿真值。图7和图8分别为优化前后的B柱加速度和侵入量曲线的对比图。

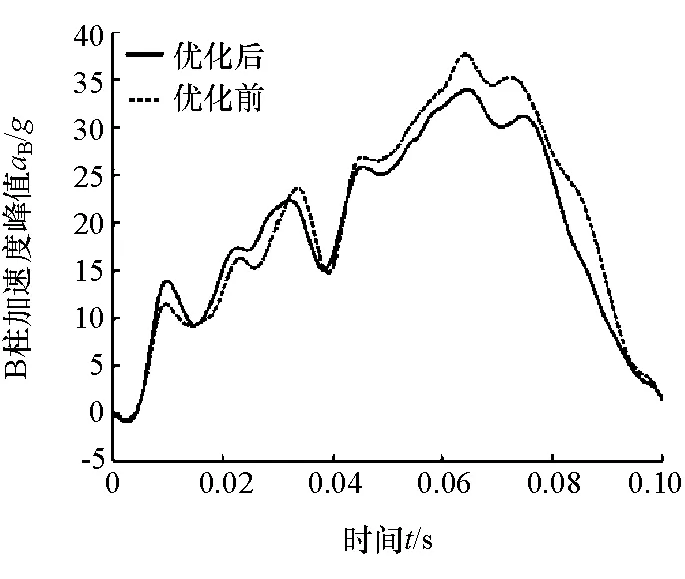
图7 优化前后B柱加速度曲线对比

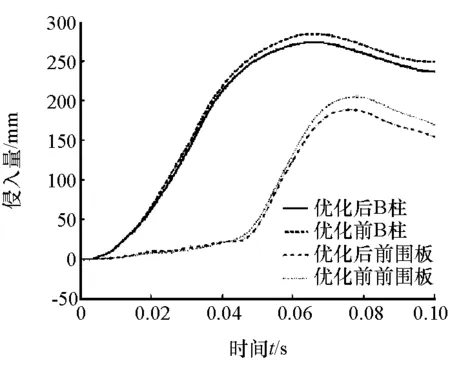
图8 优化前后侵入量曲线对比

由图7可见：优化后的B柱加速度峰值为34.03g，比初始设计的37.7g降低了9.73%；并且在碰撞40～80ms阶段，优化后的B柱加速度均小于优化前，加速度积分值从1.241g变为1.152g，减小了7.17%。由图8可见，经过多学科优化，前围板和B柱最大侵入量分别减小了3.55%和8.01%。

优化方案使碰撞安全性的3项指标均有不同程度的改善，减小了巨大冲击力和车内生存空间压缩对乘客造成的伤害，对提高乘员的安全性具有重要意义。另外，NVH和轻量化性能也通过约束设置得到了保证，多学科优化方案提高了汽车的综合性能。

5 结论

(1) 通过对比各种代理模型在测试函数和正面碰撞优化中的应用，发现组合代理模型的预测能力通常高于单一代理模型，且在多目标优化中有助于得到更满意的最优解。

(2) 将组合代理模型与协同优化方法相结合，求解车身多学科优化问题，得到Pareto前沿，可缩短新产品的开发周期，对车辆的研发有较好的指导作用。

(3) 本文中的多学科优化方案减小了B柱加速度峰值和前围板与B柱的最大侵入量等安全性指 标，提高了碰撞安全性，同时兼顾了NVH和轻量化性能。

[1] 王平,郑松林,吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报,2011,47(2):103-108.

[2] 张勇,李光耀,孙光永,等.多学科设计优化在整车轻量化设计中的应用研究[J].中国机械工程,2008,19(7):877-881.

[3] 苏瑞意,桂良进,吴章斌,等.大客车车身骨架多学科协同优化设计[J].机械工程学报,2010,46(18):128-133.

[4] 张勇,李光耀,孙光永.汽车车身耐撞性与NVH多学科设计优化研究[J].中国机械工程,2008,19(14):1760-1763.

[5] SIMPSON T W, BOOKER A J, GHOSH D, et al. Approximation methods in multidisciplinary analysis and optimization: a panel discussion[J]. Structural and Multidisciplinary Optimization,2004,27(5):302-313.

[6] 周云郊.钢铝混合材料车身结构轻量化设计关键问题与应用研究[D].广州:华南理工大学,2011.

[7] 史国宏,陈勇,杨雨泽,等.白车身多学科轻量化优化设计应用[J].机械工程学报,2012,48(8):110-114.

[8] PAN F, ZHU P, ZHANG Y. Metamodel-based lightweight design of B-pillar with TWB structure via support vector regression[J]. Computers and Structures,2010,88(1-2):36-44.

[9] GOEL T, HAFTKA R T, SHYY W, et al. Ensemble of surrogates[J]. Structural and Multidisciplinary Optimization,2007,33(3):199-216.

[10] ACAR E, RAIS-ROHANI M. Ensemble of metamodels with optimized weight factors[J]. Structural and Multidisciplinary Optimization,2009,37(3):279-294.

[11] National Crash Analysis Center. Ford taurus model 2001[EB/OL]. http:www.ncac.gwu.edu/vml/models.html.,2010.

[12] 李凡,吴光强,郭建波.基于耐撞性的多学科近似模型预测精度研究[J].汽车科技,2014(2):6-12.

[13] 玄光男,程润伟.遗传算法与工程优化[M].北京:清华大学出版社,2004.

Multidisciplinary Design Optimization of Vehicle Body Based on Ensemble Surrogates

Huang Huanjun1, Zhang Bowen1, Wu Guangqiang1,2& Li Fan1

1.SchoolofAutomotiveStudies,TongjiUniversity,Shanghai201804; 2.InstituteofIndustrialScience,UniversityofTokyo,Tokyo153-8505

The prediction abilities of four individual surrogates and two ensembles of surrogates are comparatively analyzed, and multi-objective optimizations on the safety of vehicle frontal crash are conducted based on different surrogate models with a result revealing that ensemble of surrogates not only have better prediction accuracy and robustness, but also can promote the search of optimal solutions. On the basis of above analyses, ensembles of surrogates are adopted to fit various responses to frontal crash, side impact and body-in-white modal analyses, and a model for multidisciplinary design optimization (MDO) of vehicle body structure safety is established and solved by collaborative optimization method. The results show that ensemble surrogates are conducive to getting more satisfactory optimal solutions in multi-objective optimizations and the ensemble surrogates-based MDO for vehicle-body structure effectively improves the crash safety of vehicles with good lightweight and NVH performances.

vehicle body; ensemble of surrogates; crash safety; multidisciplinary design optimization; collaborative optimization

*国家863计划项目(2012AA111802)资助。

原稿收到日期为2014年6月20日，修改稿收到日期为2015年12月23日。