基于整体驱动桥模型的准双曲面齿轮啮合分析*

刘 程，史文库，何 伟，郭年程

(吉林大学，汽车仿真与控制国家重点实验室，长春 130022)

2016180

基于整体驱动桥模型的准双曲面齿轮啮合分析*

刘 程，史文库，何 伟，郭年程

(吉林大学，汽车仿真与控制国家重点实验室，长春 130022)

针对驱动桥准双面齿轮的传统啮合分析过程中，齿轮边界条件设置与实际工作状态存在较大差异问题，建立驱动桥整体有限元模型，真实模拟准双曲面齿轮实际工况，并通过模态试验和齿根弯曲应力台架试验验证有限元模型正确性。采用软件ABAQUS/Explict对准双曲面齿轮进行准静态啮合分析，研究轮齿啮合过程中大小齿轮齿根应力和齿面接触应力的变化规律。结果表明，在轮齿啮合过程中，大齿轮齿根弯曲应力比小齿轮大，大齿轮轮齿在啮入啮出时出现边缘接触，此时大齿轮齿根部位出现较大弯曲应力；小齿轮齿面接触应力比大齿轮大，其最大值出现在齿轮完全接触时刻。

驱动桥；准双曲面齿轮；准静态啮合；弯曲应力；接触应力

前言

准双曲面齿轮是汽车驱动桥中的关键零件，为保证齿轮啮合过程中接触疲劳寿命和弯曲疲劳寿命，在设计阶段需要对齿轮进行啮合分析，以校核准双曲面齿轮疲劳寿命。准双曲面齿轮是有偏置距的螺旋锥齿轮的一种，其啮合分析可以借鉴有关螺旋锥齿轮的啮合分析方法。螺旋齿轮啮合分析主要包括接触分析和弯曲应力分析，其中接触分析主要分为无载荷接触分析(tooth contact analysis, TCA)和载荷接触分析(loaded tooth contact analysis, LTCA)。在螺旋锥齿轮载荷啮合分析方面国内外许多学者进行了大量研究。在国内，文献[1]中利用有限元方法对微型汽车主减速器准双曲面齿轮进行静力学分析，得到齿轮加载状态下的接触应力和弯曲应力；文献[2]中利用有限元方法对螺旋锥齿轮的动态啮合特性进行研究，获得不同动态参数对齿轮啮合特性的影响；文献[3]中利用有限元方法对锥齿轮加载状态下的啮合特性进行研究；文献[4]中提出了一种基于高精度数字化真实齿面的螺旋锥齿轮齿面接触分析方法，实现了含有齿形误差和安装误差螺旋锥齿轮的数字化真实齿面的构建；文献[5]中利用几何学方法对考虑边缘接触的弧齿锥齿轮承载接触进行分析研究，并利用数值规划的方法计算出齿轮的边缘接触。在国外，文献[6]中提出了一种减小螺旋锥齿轮啮合噪声的设计方法，并建立部分啮合轮齿有限元模型，在有限元分析中假定大齿轮为完全固定状态，在主动齿轮施加转矩；文献[7]中在加载状态下研究螺旋锥齿轮各种安装误差的影响，并优化机床设计参数，通过有限元计算结果表明该方法减小了齿轮接触压力；文献[8]中为螺旋锥齿轮载荷分布提出了一种新的数值计算方法，可直接由刀盘和机床参数获得锥齿轮啮合时的载荷分布。

由于真实工作中准双曲面齿轮啮合状态下的边界条件很难确定，而从国内外螺旋锥齿轮接触分析的研究中可以看出，基于有限元齿轮接触分析中，只考虑单个轮齿或整个准双曲面齿轮对，并人为加上边界条件。这些模型中存在两个主要的缺点：第一需要定义边界条件去模拟真实齿轮；第二需要对齿轮施加载荷。实际齿轮啮合过程中载荷分布在齿轮啮合区域上，而这些啮合区域事先并不知道，简单地把力矩施加在节点上并不能真实反映齿轮的载荷状况。而基于整体驱动桥对准双曲面齿轮啮合接触分析，是在驱动桥的输入端和轮毂上直接加载转速和力矩，可以模拟驱动桥齿轮的真实工作状态下的载荷和边界条件，为驱动桥齿轮的设计和优化提供指导意见，因此建立基于整体驱动桥的对准双曲面齿轮啮合接触分析具有重要意义。

本文中采用基于有限元的数值分析方法，首先建立某轻型货车后驱动桥整体有限元模型，并通过整体模态和准双曲面齿轮齿轮弯曲应力台架试验验证模型的正确性，在此基础上按照驱动桥真实工作状况施加边界条件，并对汽车匀速行驶工况下准双曲面锥齿轮进行准静态载荷啮合分析。

1 驱动桥整体有限元模型的建立

汽车后驱动桥主要由主减速器、差速器、半轴、轮毂和桥壳等部件组成，大部分部件可根据零件的图纸建立三维模型，但建立主减速器中的准双曲面齿轮齿面模型与一般渐开线直齿齿轮有较大不同，国内有很多学者对螺旋锥齿轮齿面模型的建立进行研究[9-10]，但是建立的齿面模型与实际锥齿轮的工作齿面存在差异。为准确模拟齿轮的实际齿面，本文中采用逆向工程的方法建立螺旋锥齿轮的三维模型，并按照图纸进行装配调整。在Hypermesh中对后桥部件进行网格划分，得到后桥总成有限元模型，如图1所示，图2为隐藏主减速器壳后的主减速器局部放大图。

图1 驱动桥整体有限元模型

图2 准双曲面齿轮局部放大

2 有限元模型验证

在对螺旋锥齿轮准静态啮合分析之前先通过整个后桥总成模态试验和理论计算来验证整体有限元模型的准确性，为后续动态啮合分析奠定基础。

首先把划分好的有限元网格导入到Abaqus中，并进行材料属性、相互作用关系和边界条件等参数设置。为简化模型，在建模过程中对轴承与轴，以及花键之间配合的部位简化为绑定约束。建立摄动分析步，利用lanczos求解器计算驱动桥前20阶模态频率和振型。

模态试验使用LMS模态测试系统，将后桥总成用软弹簧悬挂起来，模拟自由边界条件，试验中激励方式选择电磁激振器激励，驱动桥的悬挂方式和激振器激励位置的布置如图3所示，由模态试验测得驱动桥前20阶模态振型和频率，限于篇幅本文只取前4阶理论模态与试验模态进行对比，对比结果如表1所示。

图3 悬吊方式及激振位置

编号振型理论模态频率/Hz试验模态频率/Hz误差/%1整体前后方向1阶弯曲80.476.94.352整体上下方向1阶弯曲81.979.82.563整体前后方向2阶弯曲262.8254.23.274整体上下方向2阶弯曲285.2268.85.751阶理论计算试验测量

从表中可以看出，试验值比理论计算值稍低，这是因为在有限元相互作用关系设置中，将部件之间的有些接触约束设置为绑定约束，这样提高了驱动桥总成刚度，从而提高了理论计算模态频率。前两阶模态频率理论计算值与试验值误差在6%之内。由于试验值与理论值基本吻合，并且理论计算模态振型与试验模态振型都能相互对应，说明建立的有限元模型是正确的，可用于后续的锥齿轮动态啮合分析。

3 后驱动桥准双曲面齿轮应力分析

基于建立的有限元模型，应用Abaqus/Explicit进行准双曲面齿轮准静态啮合过程分析，限于篇幅本文只对一典型运行工况进行分析，为真实模拟汽车在100km/h匀速行驶时驱动桥工作状况，设置驱动桥的输入端的输入角速度为322rad/s,轮毂受到的道路阻力矩为656N·m。设定模拟时长为大齿轮旋转一周所需要时间，得到各齿轮任意运行时刻的接触应力。图4和图5为主减速器小、大齿轮的某一瞬时齿面接触应力图。

图4 主减速器小齿轮齿面接触应力

图5 主减速器大齿轮齿面接触应力

由图可以看出，主减速齿轮对有3对齿同时参与啮合，且轮齿不在齿面全长同时参与啮合。在此工况下轮齿啮合的过程中，大、小齿轮均是从大端啮入之后逐渐从小端啮出，逐渐地由齿面一端连续平稳地移至另一端。这也是准双曲面齿轮平稳传递动力的特点。理论上，空载时准双曲面齿轮瞬时啮合位置为一接触点[11]，受载工况下由于准双曲面齿轮啮合区域变形，瞬时接触区为一椭圆面，但由于建模精度，以及桥壳、轴承和桥壳存在的振动变形，使接触面并非标准的椭圆面。

齿轮在接触传动的过程中，齿面接触位置的拉压状态也很复杂，轮齿齿根部位一侧受压另一侧受拉，通过最大主应力云图可以直观地分析齿轮应力状态。图6和图7为小、大齿轮任意时刻的最大主应力云图。

图6 小齿轮最大主应力云图

图7 大齿轮最大主应力云图

从图中可以看出：由于齿轮啮合时相互挤压，齿面瞬时接触区位置压应力最大，其周围区域受较大的拉应力；齿面受压导致同侧齿根处弯矩较大，即存在较大的拉应力，另一侧则受压应力；在齿根处出现应力集中。

以上接触应力和弯曲应力分析结果与文献[12]一致。齿轮产生疲劳破坏的部位一般发生在最大应力处。在啮合过程中为寻找齿轮最大应力啮合位置，须对整个啮合过程中应力变化过程进行分析。为验证本文中建立模型所预测齿轮应力的准确性，首先须对齿轮啮合应力进行测试。

4 准双曲面齿轮齿根弯曲应力测试

在驱动桥总成状态下，齿轮啮合过程中齿轮接触和弯曲同时产生，二者相互联系，而由于轮齿的相对滑动，齿面接触应力不易测量，因此可以通过测量齿根弯曲应力间接验证接触应力模型的正确性，本文中通过对选定轮齿的齿根部位布置电阻应变片法进行动态应力测量，然后应用胡克定律得到齿根部位应力值，以验证动态应力结果的正确性，为后续分析提供依据。

图8 齿轮上应变片粘贴位置

驱动桥台架试验在Burkee公司生产的汽车电控动力传动系试验台上进行，采用BX120-1AA型电阻应变片、SR20M型集流环和LMS数据采集器。由于准双曲面齿轮啮合时，齿根间隙很小，为了避免测试时应变片和连线机械损失，并测量齿轮从啮入到啮出齿根弯曲应力变化，在大齿轮的啮入、完全啮合和啮出齿根各布置对应位置测点，最终确定的测点位置如图8所示。应变片引线通过集流环从桥壳引出，最后用连接线联通到数据采集器。试验工况与第2节中齿轮的模拟工况相同。

测试数据与模拟结果对比如图9所示。从图中可以看出，仿真结果与测试结果在A，B和C 3点变化趋势基本一致，最小相对误差在9%以内，最大相对误差在16%以内，仿真结果较好，说明有限元仿真结果可信，可进一步用于齿轮接触应力和弯曲应力分析。

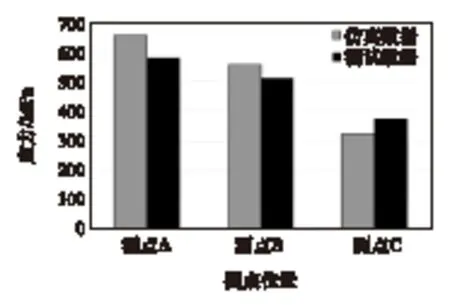
图9 齿根弯曲应力仿真与测试结果对比图

5 齿轮接触应力和弯曲应力分布分析

5.1 齿根弯曲应力分布分析

图10 齿轮齿根受拉侧等效应力分布图

由于准双曲面齿轮中每个轮齿啮合过程基本相同，因此只需对一个轮齿的啮合过程进行分析。选取大齿轮任意一个轮齿两侧齿根部位的节点和与其相对应啮合小齿轮轮齿两侧齿根部位节点进行弯曲应力分析。在齿轮从啮入到啮出过程中，齿根部位等效弯曲应力如图10和图11所示。

图11 齿轮齿根受压侧等效应力分布图

由图可见：大小齿轮上齿根部位应力变化基本相同；齿轮在啮入和啮出过程中，存在齿端接触现象，小齿轮的齿顶与大齿轮齿面发生接触，导致大小齿轮啮入阶段靠近齿轮大端侧应力较大，啮出阶段靠近齿轮小端应力较大，从而引起齿根受拉侧弯曲应力集中；在啮合开始阶段，齿根受拉侧的应力较大，随着齿轮转动，齿根所受应力逐渐减小，当轮齿退出啮合时，齿端的应力又增大。由于大齿轮受到的力矩要大于小齿轮，大齿轮比小齿轮对应时刻齿根受拉侧等效应力大。大齿轮的齿端效应要比小齿轮显著，主要由于小齿轮的齿面宽度大于大齿轮，小齿轮啮入和啮齿出位置不在轮齿边缘。

齿轮受压侧等效应力与受拉侧变化规律基本相同，齿轮在啮合过程中，齿轮的一端受到拉应力另一侧必然会受到压应力，由于齿轮材料抗压强度要比抗拉强度大，因此齿轮啮合过程中受压侧不易产生疲劳破坏。对比齿轮受拉侧弯曲应力与受压侧弯曲应力可知，准双曲面齿轮啮合过程中，齿根弯曲应力出现在大齿轮进入啮合位置的受拉侧齿根位置。

5.2 齿面接触应力分布分析

接触应力是导致接触疲劳破坏主要原因，为保证齿轮接触疲劳可靠性须对齿轮接触应力进行分析。本文中取轮齿相互接触面上分度圆上节点作为研究对象，节点移动方向为从大端指向小端。大小齿轮节点位置的接触应力对比如图12所示。

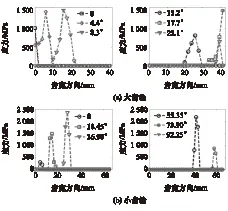
图12 齿轮轮齿接触面接触应力分布图

由图可见：在齿轮啮合过程中齿面接触应力先增大后减小，大小齿轮都是在同一时刻接触应力出现最大值，在齿轮完全啮合时接触应力值达到最大。这是由于处于完全啮合状态的齿轮啮合力较大，处于啮入和啮出的齿轮所受啮合力较小。由于小齿轮比大齿轮转速高，动载荷的影响导致小齿轮的接触应力要比大齿轮大。从接触应力分布可以看出小齿轮接触应力要比大齿轮接触应力要大，小齿轮在完全接触时应力最大值出现在齿轮完全啮合时刻。

5 结论

(1) 建立包含轮毂在内驱动桥整体有限元模型，并通过整体模态试验和齿根弯曲应力试验验证了模型的正确性。

(2) 对准双曲面齿轮啮合时接触应力和最大主应力分析，结果表明，准双曲面齿轮在啮合过程中，齿面接触由轮齿大端逐渐过渡到小端，接触印迹接近椭圆，由于轮齿的啮合接触导致接触面齿根受拉，非接触面齿根部位受压。

(3) 对齿轮啮合过程中接触应力和弯曲应力分布进行分析，结果表明，齿根部位受拉侧等效弯曲应力比受压侧大，大齿轮齿根弯曲应力比小齿轮大，大齿轮容易出现齿端边缘接触，导致齿轮在啮入啮出时弯曲应力较大。小齿轮齿面接触应力比大齿轮大，最大接触应力出现在齿轮完全啮合时刻。

[1] 万尚国.微车主减速器准双曲面齿轮静力学有限元分析[D].武汉:武汉理工大学,2010.

[2] 唐进元,彭方进.准双曲面齿轮动态啮合性能的有限元分析研究[J].振动与冲击,2011(7):101-106.

[3] 蒲太平.螺旋锥齿轮加载接触分析及啮合刚度的有限元计算方法研究[D].长沙:中南大学,2010.

[4] 汪中厚,李刚,久保爱三.基于数字化真实齿面的螺旋锥齿轮齿面接触分析[J].机械工程学报,2014,50(15):1-11.

[5] 方宗德,邓效忠,任东锋.考虑边缘接触的弧齿锥齿轮承载接触分析[J].机械工程学报,2002,38(9):69-72.

[6] LITVIN F L, VECCHIATO D, YUKISHIMA K, et al . Reduction of noise of loaded and unloaded misaligned gear drives[J]. Computer Methods in Applied Mechanics and Engineering,2006,195(41):5523-5536.

[7] SIMON V. Machine-tool settings to reduce the sensitivity of spiral bevel gears to tooth errors and misalignments[J]. Journal of Mechanical Design,2008,130(8):082603-1-082603-10.

[8] KOLIVAND M, KAHRAMAN A. A load distribution model for hypoid gears using ease-off topography and shell theory[J]. Mechanism and Machine Theory,2009,44(10):1848-1865.

[9] 彭方进.基于接触动力学的螺旋锥齿轮动态啮合性能有限元分析研究[D].长沙:中南大学,2010.

[10] 祝政委.弧齿锥齿轮参数化设计及有限元分析[D].合肥:合肥工业大学,2012.

[11] LITVIN F L, FUENTES A, HAYASAKA K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears[J]. Mechanism and Machine Theory,2006,41.

[12] LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. Cambridge University Press, Cambridge,2004.

Meshing Analysis of Hypoid Gears Based on Complete Drive Axle Model

Liu Cheng, Shi Wenku, He Wei & Guo Niancheng

JilinUniversity,StateKeyLaboratoryofAutomotiveSimulationandControl,Changchun130022

In view of the big difference between the boundary conditions set and actual working states of gears during the process of traditional hypoid gear meshing analysis in drive axle, a finite element model for the complete driving axle is built to truly simulate the actual working conditions of hypoid gears, with the model verified by a modal test and a bench test of the bending stress of tooth root. Then a quasi-static meshing analysis of hypoid gears is conducted with software ABAQUS/Explicit to study the changing law of tooth root bending stress and tooth face contact stress of both pinion and crown gears in gear meshing process. The results show that during gear meshing process, the tooth root bending stress of crown gear is higher than that of pinion gear, the edge contact occurs when the tooth of crown gear is getting into and out of engagement, causing a higher bending stress in the tooth root of crown gear, and the tooth face contact stress of pinion gear is higher than that of crown gear, with its peak appears at the moment of full contact of gears.

drive axle; hypoid gears; quasi-static meshing; bending stress; contact stress

*国家自然科学基金(51205158)、中国博士后科学基金面上项目(2013M541294)和吉林省重大科技专项(212E362415)资助。

原稿收到日期为2015年7月10日，修改稿收到日期为2015年11月23日。