车辆变速器齿轮轴系和箱体动力学耦合研究*

符升平，李胜波，罗 宁，钟铭恩

(厦门理工学院机械与汽车工程学院，厦门 361024)

2016170

车辆变速器齿轮轴系和箱体动力学耦合研究*

符升平，李胜波，罗 宁，钟铭恩

(厦门理工学院机械与汽车工程学院，厦门 361024)

为定量分析变速器齿轮轴系动态特性和箱体弹性变形的相互影响，本文中建立了车辆变速器齿轮轴系和箱体动力学耦合模型并进行求解。首先，以某履带式车辆变速器为对象，采用有限元分析和试验方法探明箱体的弹性特征，提出变速器动力学耦合的方法，建立包含弹性箱体的变速器动力学耦合模型；接着对稳态工况下变速器箱体的变形和箱体变形状态下齿轮轴系动态特性的变化进行仿真；最后通过实车道路试验，测试了箱体危险区域的振动加速度，验证了所建变速器动力学耦合模型的正确性，完善了变速器动力学耦合性能的预测方法。

车辆变速器；箱体弹性变形；齿轮轴系特性；动力学耦合模型；仿真；实车试验

前言

变速器是车辆关键的动力传动部件，包括齿轮轴系和箱体，是一个复杂的弹性机械系统，影响车辆行驶的安全性和舒适性。变速器齿轮轴系受到发动机波动转矩、路面负载、齿轮动态啮合力等多源动态激励的作用，产生弯扭耦合振动，通过滚动轴承的支反力，加剧箱体的变形，改变箱体表面的应力状态；箱体变形和应力分布状态的变化改变齿轮轴系支承刚度和支承阻尼等参数，影响齿轮轴系的动力学特性。因此变速器工作时，箱体和齿轮轴系产生动力学耦合效应，表征复杂的动力学行为，影响箱体动态强度和齿轮轴系的动态响应。以某车辆变速器为对象，建立箱体结构系统和齿轮轴系的动力学耦合模型，分析其动力学耦合特征，是对齿轮系统动力学研究的重要补充。

目前，齿轮系统耦合动力学的研究在内容上局限于分析船用齿轮箱、风电齿轮箱、汽车轮边减速器等的耦合动态特性，针对多个挡位的车辆变速器等更复杂的齿轮系统研究甚少；在研究方法上通常采用集中参数法和有限元法，存在集中参数法不能全面预测系统在空间域内的动态特性和有限元法不能求解结构大位移变形的局限性[1-14]。

现有车辆变速器耦合动态特性的研究如下：文献[15]中基于齿轮轴系的扭转振动模型，优化变速器几何设计参数，降低变速器的振动噪声；文献[16]中探明了车辆换挡过程中换挡瞬态特性对箱体振动有重大影响；文献[17]中分析了变速器箱体的变形对齿轮轴系动态性能的影响；文献[18]～文献[21]中在时域和频域上分析了多源动态激励下变速器箱体的动态响应。上述研究独立分析了齿轮轴系的动态性能对箱体振动的影响和箱体弹性效应下的齿轮轴系动态特性，动力学耦合程度较弱。

综上所述，建立多源动态激励作用下车辆变速器齿轮轴系和箱体动力学耦合的模型，深入研究变速器齿轮轴系和箱体的动力学耦合行为，有一定的理论和工程价值。本文中以某履带车辆变速器为例，仿真和试验研究箱体弹性特征，提出齿轮轴系和箱体动力学耦合的方法，建立和求解变速器动力学耦合模型，仿真分析动态耦合特性，最后采用实车道路试验对仿真结果进行验证。

1 研究对象简介

图1 变速器传动简图

某履带车辆3自由度多级定轴齿轮变速器传动简图如图1所示。通过操纵齿轮轴系中的换挡离合器(C1，C2，C3，CL，CH和CR)，实现不同挡位之间的切换，挡位的操纵元件如表1所示。

表1 挡位的操纵件列表

注：“●”表示离合器接合。

本文中研究稳态工况下齿轮系统的耦合动态特性，因此不考虑湿式换挡离合器的分离和接合过程。由于变速器在高速条件下产生振动剧烈、噪声过大等现象，因此第6挡被选为研究工况，其功率流如图1中箭头所示。

2 箱体的弹性化

箱体弹性化是分析变速器耦合动力学特性的前提，本文中将采用仿真与试验相结合的方法分析箱体弹性特征。

2.1 箱体有限元模型的建立

变速器箱体是一个复杂的薄壁空间构件。以保证最大程度上接近箱体实际结构和能反映箱体实际物理特性为原则，通过几何清理、网格划分(15和10mm的1阶四面体实体单元)、定义材料属性(箱体材料为铸铝合金ZL101A)和边界条件等，建立箱体的有限元模型，共计440 506个实体单元，如图2所示。

图2 箱体有限元模型

2.2 箱体自由模态的仿真分析

采用Lanczos法计算箱体的自由模态，得到箱体前20阶模态的固有频率和对应振型：第19阶和第20阶是箱体的整体模态，多处有较大变形；其余各低阶模态(<20)的最大振型均出现在箱体局部。以第9阶、第19阶和第20阶模态为例进行分析，其振型如图3所示。

图3 箱体振型图

由图3可知，振幅较大的位置(方框标识处)主要集中在上下箱体中间与右侧肋板和轴承座孔周围等处，这些部位在外部激励条件下更容易产生变形。

2.3 试验模态的分析和验证

本试验采用锤击法对箱体整体进行模态试验，试验设备包括丹麦B&K公司8206型激振锤、4326型3向加速度传感器、LMS公司SC10DC-UTP型数据采集设备和LMS Test.Lab数据分析软件等。根据测点布置遵循避开节点位置等原则，共得到整箱170个测点，如图4所示。

为避免环境振动和支承刚度对测试的影响，采用自由悬挂法模拟箱体的自由状态：利用软绳在适当位置将箱体悬挂在液压小车支架上，并进行适当调整，使悬挂后的箱体保持水平，如图5所示。

图4 整箱测点布置图

图5 整箱自由状态模拟

在LMS.Test.Lab环境下建立箱体的试验模型，使测点坐标和试验模型中的节点位置相对应。基于自由模态试验结果，采用PolyMAX方法，即在极大似然估计原理基础上，对试验测得的频响函数进行处理，识别出箱体的模态参数。箱体前20阶有限元模态和试验模态固有频率的对比如表2所示。

表2 试验结果与数值计算结果的对比

由于试验中箱体分解不彻底，保留了液压阀、螺栓轴承等零部件，固有频率的仿真值与试验值存在一定的误差。但由表2可知，最大相对误差在6%以内，证明了箱体有限元模型的准确性。

3 齿轮系统耦合方法

在变速器工作过程中，齿轮啮合力、发动机激励和路面载荷通过轴承的支承效应使箱体产生振动，同时箱体弹性变形通过轴承支承影响齿轮轴系的动态特性，因此变速器耦合动力学模型建立的关键是抽象箱体、轴承和传动轴之间的数学关系。

轴承的支承效应用刚度阻尼矩阵表示。箱体和传动轴经过弹性化处理离散成n个质量单元，通过单元外节点之间的位移约束条件，生成具有综合变形能力的弹性体。每个节点的广义坐标用模态参数描述，位移约束条件抽象为弹簧阻尼力，则某方向上的箱体-轴承-传动轴动力学模型如图6所示。

图6 箱体-轴承-传动轴动力学模型

对应的数学模型为

式中：下标n表示箱体质量单元数目；下标m表示传动轴质量单元数目；下标x表示箱体；下标b表示轴承；下标z表示传动轴；xxi为传动轴或箱体质量单元的综合广义位移；kxi和cxi分别为箱体离散单元之间等效刚度和阻尼系数；kzi和czi为传动轴离散单元之间等效刚度和阻尼系数，与本身结构参数有关。

此数学模型把轴承的支承效应等效为刚度阻尼元素，能描述箱体在各轴承处外节点位移与传动轴在各轴承处外节点位移间的耦合效应，实现动态激励的传递、箱体变形和齿轮轴系动力学行为之间的耦合。

4 变速器耦合动力学模型的建立

齿轮轴系主要包括齿轮副、滚动轴承、湿式换挡离合器、传动轴等零部件。仿真条件为发动机额定转速2 000r/min下的第6挡稳态工况，发动机额定功率为588kW；变速器功率传递路径为Z26-Z33-Z21-Z37，几何参数如表3所示；滚动轴承结构参数如表4所示。

表3 啮合齿轮副的几何参数

在第6挡工况下，齿轮轴系中不工作的齿轮副等效为集中惯量，工作的齿轮副在ADAMS中建立对应的动力学模型：在传统齿轮副扭转动力学模型基础上，在主动齿轮和被动齿轮中间添加一无质量刚性中介齿轮。主动齿轮通过齿轮副与中介齿轮保 证运动学关系；中介齿轮与被动齿轮通过扭簧传递动力，设置扭簧的性能参数可以模拟动态激励，对应的动力学模型如图7所示。

表4 各滚动轴承的几何参数

图7 齿轮副动力学模型

与图7对应的数学模型为

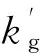
[22]中滚动轴承支承刚度和阻尼的计算方法，结合表4中各轴承的几何参数，得到在上述仿真条件下各轴承的支承刚度和阻尼，如图8所示(以轴承4为例，坐标轴方向参考图1)。

图8 轴承4刚度和阻尼时变曲线

未参与动力传递的湿式换挡离合器等效为集中惯量，接合状态下传递转矩MCC为

MCC=μdReqzFnon

式中：Req为摩擦片有效半径；z为摩擦副数；Fnon为接触压力；μd为动摩擦因数。

对传动轴通过弹性化处理，以能被ADAMS识别的模态中性文件建立传动轴的动力学模型(如图9所示)。

图9 第1轴动力学模型

图10 齿轮变速器动力学耦合模型

忽略路面不平度在垂直方向上对齿轮箱体的动态载荷，考虑齿轮副、轴承等多源动态激励，基于动态子结构理论和多体动力学，参考文献[21]中齿轮轴系动力学建模方法，综合上述建立的箱体有限元模型和提出的齿轮系统动力学耦合方法，在ADAMS环境中建立多源激励下变速器动力学耦合模型，如图10所示。

5 仿真结果分析

采用ADAMS中GSTIFF积分器进行求解，时间步长取0.01，可视化仿真变速器第6挡稳态工况的动态特性：以运动学参数、载荷特性和动态响应为例，探讨箱体弹性效应对齿轮轴系动态特性的影响。

5.1 运动学参数

变速器输出转速是重要的运动学参数，分析箱体变形对其产生的影响，结果如图11所示。

图11 输出转速

由图11可知，两条曲线完全重合，表明箱体弹性对变速器输出转速没有影响，运动学参数只与系统动力输入输出条件和齿轮参数等传动特征参数相关。当系统工作在第6挡稳态工况时，由于发动机转矩波动和传动轴弹性效应等因素，输出转速在平均转速4 850r/min附近波动。

5.2 载荷特性

动态载荷是反映系统动态特性的重要参数，对比分析箱体弹性特征对齿轮啮合力和轴承支反力的影响，结果如图12和图13所示。

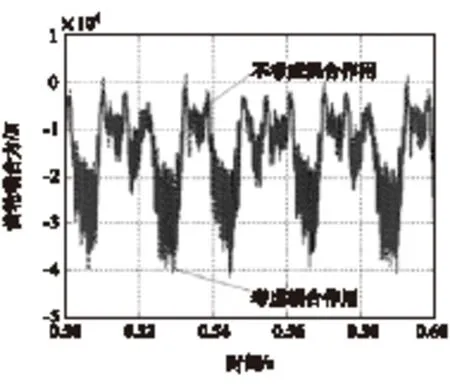
图12 第1对啮合齿轮y向啮合力

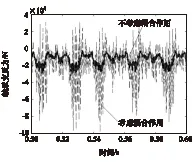
图13 轴承6 y向支反力

由图12可知，箱体弹性对齿轮啮合力的影响很小，两种情况下变化趋势一致，且都与齿轮运动状态相符。不考虑耦合作用，其平均值为-17 757.90N，峰值为-40 461.36N；考虑耦合作用，其平均值为-17 907.41N，峰值为-41 629.57N。两者相对误差分别为0.84%和2.89%，表明齿轮副参数和动力边界条件是决定齿轮啮合力的主要因素。

图13为6号轴承y向支反力的时间历程。由图可见，两种条件下的支反力按同一周期变化，但是幅值差异较大。弹性箱体下，支反力波动剧烈，平均值为-18 497.607 7N；不考虑耦合作用，支反力变化均匀，幅值波动平缓，平均值为-12 951.937 8N。数据表明箱体弹性效应对轴承支反力影响较大。根据位移协调条件，箱体表面变形会加剧轴承相应界面节点的变形，而轴承简化为刚度阻尼，界面节点的变形将提高轴承的等效变形，使支反力增加。

5.3 动态响应

齿轮轴系在多源激励作用下的动态响应是齿轮变速器动力学研究的重要内容。对比研究第2轴上与齿轮b接触区域表面节点的位移和加速度响应，结果如图14所示。

图14 第2轴上与齿轮b接触区域表 面节点的振动位移和加速度

由图14可知，箱体弹性对齿轮轴系的动态响应有很大的影响，考虑耦合作用时，动态响应波动范围明显扩大，变化剧烈，说明箱体变形与齿轮轴系的动态响应是相互耦合的，箱体受到动态支反力的作用产生相应的动力学行为，使局部结构的变形增大，轴承传递箱体变形产生的动态附加载荷，加剧传动轴的振动，改变齿轮传动系统动态特性。

6 试验验证

为验证上述变速器动力学耦合模型的正确性，通过实车道路试验，对比分析实车行驶和仿真条件下箱体表面的动态响应。

试验选用丹麦B&K公司4326型三向加速度传感器获得振动信号，通过电荷转换，采用LMS公司SC10DC-UTP型数据采集设备进行采集，最后在LMS Test. Lab中完成数据分析，获得箱体表面加速度响应。

实车试验路面为水泥路面，对每个挡位多个稳定车速下的加速度响应进行测试。由于篇幅限制，只对比验证6挡下车速为70km/h(发动机转速为2 000r/min)的工况。

选取箱体表面振动响应较大的点作为测点，如图15所示。其中表面8个测点安装了三向加速度传感器，箱体左右支承和前盖箱体左右支架和前盖处3个传感器为单向传感器。

图15 测点布置

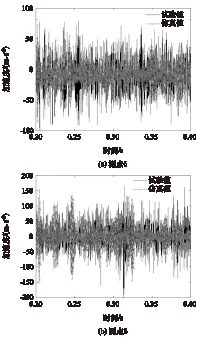
图16 滤波后时域对比结果

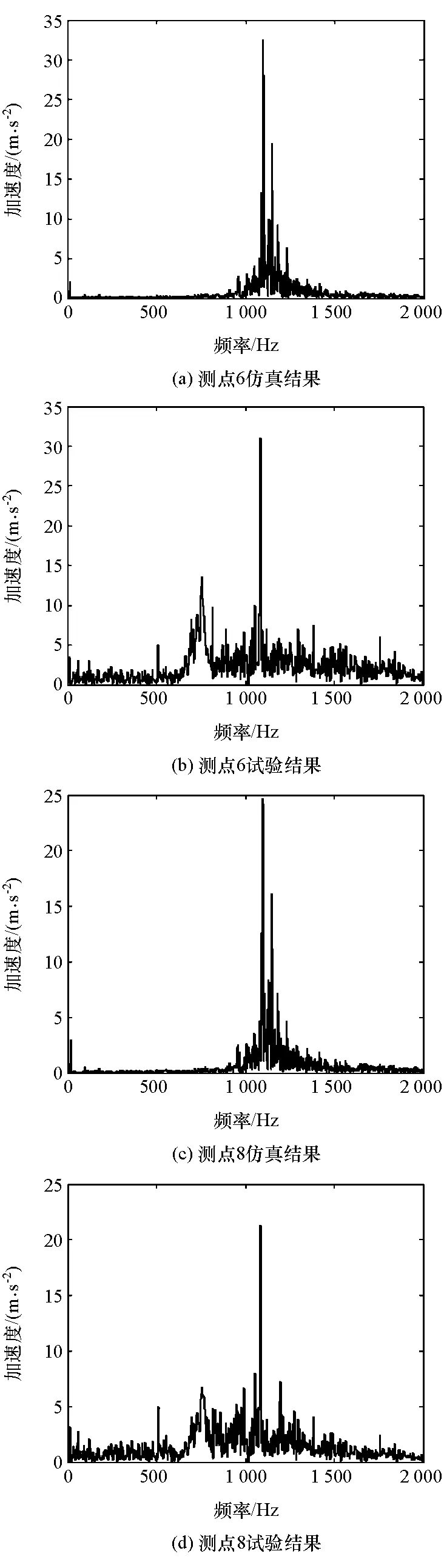
图17 滤波后频域对比结果

选用路面情况良好的A级水泥路作为仿真路面。由于试验结果主峰值出现在2 000Hz以下，高频峰值是噪声引起的低峰值，因此低通滤波试验加速度响应，截止频率为2 000Hz。由于仿真结果不存在前后传动啮合齿轮激励，其基频为760，1 056和1 200Hz，因此采用带阻滤波器，阻带范围为基频±10Hz。图16和图17分别为滤波后测点的法向振动加速度在时域和频域中的对比结果。表5为滤波后仿真和试验下各测点法向振动加速度均方根值和误差。

表5 法向振动加速度均方根值 m·s-2

由图16、图17和表5可知，通过滤波处理后，时域中两者变化趋势比较接近，频域中两者的主频和幅值相吻合。各测点的试验和仿真均方根值最大误差为32.6%，且试验值比仿真值大，主要原因：(1)实车试验中，由于噪声的影响，在整个频段内出现低峰值，导致试验结果均方根值偏大；(2)实车试验中，路面不平度会引起变速器箱体的垂直振动，但是仿真模型没有考虑路面垂直激励的影响，故仿真结果均方根值偏小；(3)建模过程中没有考虑各零部件之间的摩擦与冲击和各部件的弹性与阻尼特征，因此简化因素和假设条件使仿真结果均方根值偏小。

7 结论

(1) 建立了箱体-轴承-传动轴动力学模型，它以数学式描述了箱体、轴承和传动轴之间的动力学关系，实现了齿轮轴系和箱体的动态耦合，为建立变速器动力学耦合模型提供理论基础。

(2) 建立了变速器的动力学耦合模型，仿真分析了箱体弹性对齿轮轴系动态特性的影响，结果表明：系统运动学参数只与动力条件和齿轮副参数等相关；齿轮动态啮合力主要取决于其结构参数和动力边界条件；箱体弹性对轴承支反力和传动轴动态响应有较大影响，加剧了轴承支反力和动态响应幅值的波动。

(3) 采用路面实车试验测试了箱体表面的振动加速度，对比分析了滤波后的试验数据和仿真结果，结果表明：时域中两者变化趋势一致，箱体的振动加速度主要由齿轮啮合激励引起；仿真建模中没有考虑路面垂直激励、试验噪声和仿真假设条件等的影响，造成测点均方根值的仿真结果小于试验结果，最大误差为32.6%。

(4) 该研究为车辆变速器的耦合振动特性的深入分析提供了新的方法，可指导齿轮箱动态优化设计和振动控制的研究。

参考文献

[1] 杨成云.齿轮传动系统耦合振动响应及抗冲击性能研究[D].重庆:重庆大学,2006.

[2] 朱才朝,陆波,宋朝省,等.大功率船用齿轮箱系统耦合非线性动态特性研究[J].机械工程学报,2009,45(9):31-35.

[3] 陆波,朱才朝,宋朝省,等.大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J].振动与冲击,2009,28(4):76-80.

[4] 朱才朝,陆波,徐向阳,等.大功率船用齿轮箱系统热弹耦合分析[J].船舶力学,2011,15(8):898-905.

[5] 朱才朝,陆波,徐向阳,等.大功率船用齿轮箱传动系统和机构系统耦合特性分析[J].船舶力学,2011,15(11):1315-1321.

[6] 魏超.大型船用齿轮箱系统动态性能分析方法研究[D].杭州:浙江大学,2013.

[7] 王海霞.小倾角船用齿轮箱接触分析及动态特性研究[D].重庆:重庆大学,2010.

[8] 许洪斌,吴灿元,杨长辉.大型风电齿轮箱耦合固有特性仿真分析[J].机械设计与制造,2014,5(5):192-194.

[9] 王庆,张以都.二级圆柱斜齿轮系统耦合动态响应分析[J].振动与冲击,2012,31(10):87-91.

[10] 郑站强.风电齿轮箱动态特性研究与工作模态测量分析[D].重庆:重庆大学,2011.

[11] 吕世志.专用打印机齿轮系统耦合振动分析[D].哈尔滨:哈尔滨工业大学,2012.

[12] 刘建培.汽车轮边减速器系统耦合动态特性分析及动态响应优化[D].重庆:重庆大学,2014.

[13] 肖正明,秦大同,尹志宏.多级行星齿轮系统耦合动力学分析与试验研究[J].机械工程学报,2012,48(23):51-58.

[14] 薛强,李顺德,冯广斌.试验台齿轮箱系统耦合振动有限元模态分析[J].机械传动,2010,34(9):65-68.

[15] Mehmet Bozca. Torsional vibration model based on optimization of gearbox geometric design parameters to reduce rattle noise in an automotive transmission[J]. Mechanism and Machine Theory,2010,45:1583-1598.

[16] Taehyun Shim, ZHANG Yi. Effects of transient power train shift dynamics on vehicle handling[J]. International Journal of Vehicle Design,2006,40(1-3):159-174.

[17] 贺敬良,何畅然,吴序堂,等.变速器结构柔性对动态特性的影响分析[J].中国机械工程,2015,26(15):2010-2015.

[18] 刘辉,张喜清,项昌乐.多源动态激励下变速器箱体结构的动态响应分析[J].兵工学报,2011,32(2):129-134.

[19] ZEN G W, ZHU X Z, WEI Z J. Study on nonlinear dynamic response of the gear-shaft-housing coupling system[C]. 2010 International Conference on Advanced Mechanical Engineering, September4-4,2010, Luoyang, China,2010:805-808.

[20] ABBES M S, TRIGUI M, CHAARI F, et al. Dynamic behavior modeling of a flexible gear system by the elastic foundation theory in presence of defects[J]. European Journal of Mechanics-A/Solids,2010,29(5):887-896.

[21] Mohamed Slim Abbes, Thar Fakhfakh, Mohamed Haddar, et al. Effects of transmission error on the dynamic behavior of gearbox housing[J]. International Journal of Advanced Manufacture Technology,2007,34:211-218.

[22] FU Shengping, XIANG Changle. Numerical calculation of ball bearing excitation and application in multi-body dynamics simulation[C]. IEEE 10th International Conference on Computer-Aided Industrial Design and Conceptual Design, Wenzhou, China,2009:596-600.

[23] LIU Hui, FU Shengping, XIANG Changle. Multi-body dynamics simulation of a tracked vehicle power train in consideration of multi-source excitations[J]. International Journal of Computational Intelligence System,2011,4(3):314-320.

A Research on Dynamics Coupling Between Gear Shaftsand Housing in a Vehicle Transmission

Fu Shengping, Li Shengbo, Luo Ning & Zhong Ming’en

SchoolofMechanicalandAutomotiveEngineering,XiamenUniversityofTechnology,Xiamen361024

To quantitatively analyze the interaction between the dynamics characteristics of gear shafts and the elastic deformation of housing of transmission, a dynamics model for the coupling between gear shafts and housing of vehicle transmission is set up and resolved in this paper. Firstly, with the transmission of a tracked vehicle as object, the elastic features of its housing is investigated by both finite element analysis and test, a method of dynamic coupling of transmission is proposed, and a dynamically coupled model for the transmission with elastic housing is built. Then a simulation is conducted on the deformation of housing under steady condition and the changes in dynamic characteristics of gear shafts under the deformed state of housing of transmission. Finally a real vehicle road test is performed to measure the vibration accelerations at the dangerous areas of housing, verifying the correctness of the dynamically coupled model for transmission built and perfecting the prediction method of coupled dynamic performance of transmission.

vehicle transmission; housing elastic deformation; gear shafts characteristics; dynamically coupled model; simulation; real vehicle test

*国家自然科学基金(51505402和51405410)和福建省中青年教师教育科研项目A类(JA14245)资助。

原稿收到日期为2015年4月15日，修改稿收到日期为2015年11月22日。