寒区隧道温度场的时空演化规律及温控措施研究
2016-04-10周小涵曾艳华周晓军
周小涵,曾艳华,范 磊,周晓军
(1.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031;2.中铁大桥勘测设计院集团有限公司,湖北 武汉 430050;3.中铁二院工程集团有限责任公司 土建一院隧道所,四川 成都 610031)
寒区隧道温度场的准确预测有助于设计者选择合适的防寒抗冻措施。国内学者对多条寒区隧道进行了温度场的现场监测及研究[1-5]。张耀等[6-7]通过对隧道现场实测气温资料的整理,建立了圆形隧道传热方程,得到了寒区有隔热层的圆形隧道温度场解析解和简化计算方法。肖琳等[8]利用模型试验,探讨了地铁隧道围岩内部温度场的分布规律。M.Krarti等[9]根据能量守恒原理获得了地下风洞内气体温度场的解析解。YM Lai等[10]采用摄动技术,通过无量纲法推导出圆形隧道冻结过程温度场的解析解。Prashant K J等[11],Suneet S[12]等利用叠加原理和分离变量方法得到了圆形断面隧道在考虑温度随坐标变化的对流边界条件下瞬态温度场的解析解。夏才初等[13]计算了考虑衬砌和隔热层的寒区隧道温度场解析解。陈功胜[14]研究了巷道围岩调热圈半径及温度场分布规律。江亦元[15]和王引生[16]分别对寒区昆仑山隧道的排水系统进行了保暖的探讨和试验研究。这些研究得到了关于寒区隧道温度场的解析计算公式及隔热层简化计算方法,而以隧道洞口风温及洞内风速为边界条件,同时考虑空气、衬砌、保温隔热层和围岩的对流换热和热传导耦合作用的研究还未见报道。
本文推导寒区隧道围岩—衬砌—气流的非稳态热传导的有限差分方程,以在建的牡绥铁路绥阳隧道为例,计算分析寒区隧道温度场随通风时间的变化规律以及隔热层对寒区隧道温度场的影响规律等;并与现场的实测温度场对比,验证有限差分方程的准确度。
1 理论推导
在寒区隧道围岩—衬砌—气流传热系统中,冷空气与隧道衬砌和围岩进行热交换,引起隧道围岩温度的降低。能量交换存在热传导、对流换热和热辐射3种方式:围岩与隧道衬砌之间的能量交换属于热传导;衬砌与隧道内气流之间的传热则既含有对流换热,又有热辐射,相对于对流换热而言,热辐射引起的热量传递很小,在此忽略不计;同时隧道内的气流自身也存在热交换,这种热交换使得隧道内的气流温度趋于平均分布。故隧道围岩—衬砌—气流系统的传热过程主要是指围岩与隧道衬砌的热传导和隧道衬砌与气流之间的对流换热。
1.1 隧道温度场的控制方程
隧道温度场计算模型如图1所示,图中R为隧道洞室当量半径。
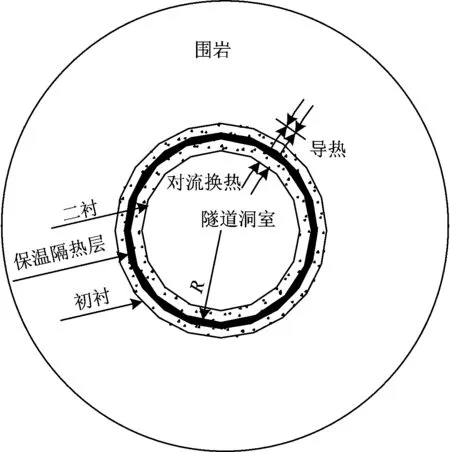
图1 隧道温度场计算模型
隧道温度场的形成及重新调整属于热传导过程,笛卡尔坐标系中三维非稳态热传导微分方程的一般形式[17]为

(1)
式中:ρ为衬砌或围岩的密度,kg·m-3;cp为衬砌或围岩的恒压比热容,J·(kg·℃)-1;λ为衬砌或围岩的导热系数, W·(m·℃)-1;t为衬砌或围岩内部任一点的温度,℃;τ为通风时间,s;φ为单位时间内通过某一给定面积的热量,W。
隧道围岩的径向传热量远大于其轴向[13],隧道断面面积相对于研究区域很小,洞内气温只沿隧道轴线方向变化;假定围岩的导热系数λ为常数,温度场是无内热源的稳态分布;则微分方程(1)可转化为如下柱坐标系下的计算方程。
(2)
式中:r为衬砌或围岩中任一点到隧道中心的距离,m。
1.2 隧道温度场计算模型的离散化
隧道贯通后,受到气流温度影响的围岩厚度(调热圈)增大,并最终到达极限值。隧道断面内非稳态传热分析基于如下假定:隧道横断面为圆形,其直径采用当量直径;对于围岩和每一种衬砌而言,都为独立的、各向同性的、均匀的连续介质;在计算零时刻,衬砌温度等于围岩原始温度,围岩原始温度沿径向不变;隧道内气流与壁面发生对流换热。
沿径向,将二衬、初支和隔热层按等厚划分网格。为计算精确且节省时间,将隧道外围岩区域划分为2部分,如图2所示。第1部分为D1(r≤10R),步长为Δr1;第2部分为D2(r>10R),步长为Δr2,Δr1<Δr2。图2中:节点1为对流边界,节点6,8,13为复合材料传热边界,节点14为围岩内部的点。
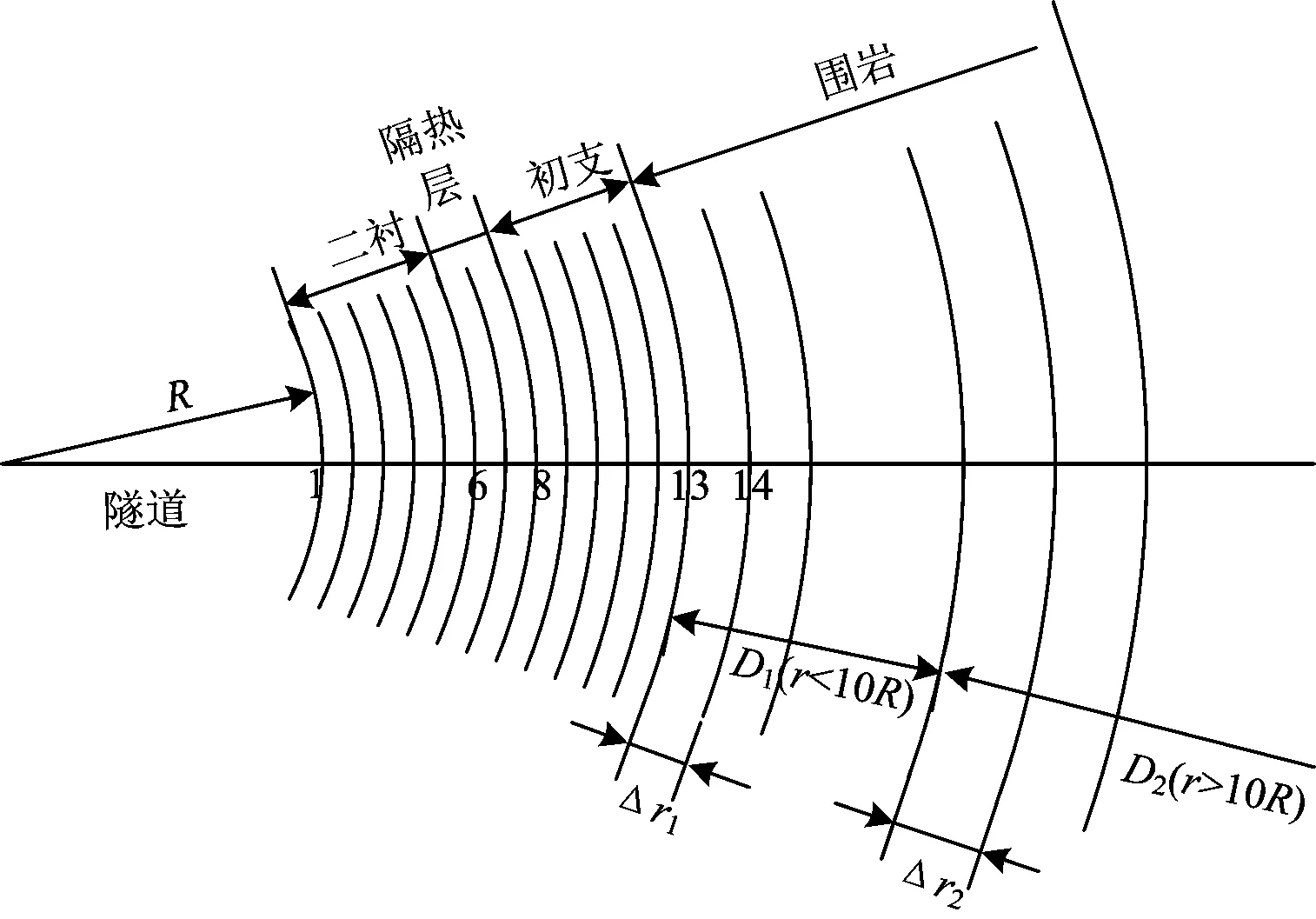
图2 断面内差分节点划分示意图
1.3 有限差分方程
1.3.1围岩温度的近似表达式
用偏微分方程的替代法建立中心有限差分方程,求出其一阶、二阶偏导数并代入式(2)中,可得围岩内部节点j(j≥14)的温度tj, n+1的近似计算式为
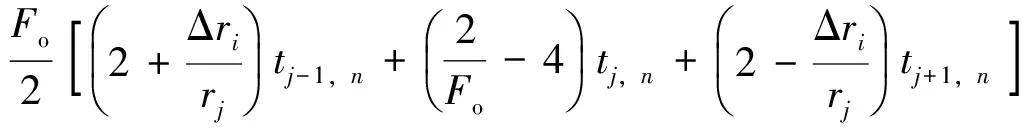
(3)
其中,
式中:tj,n+1为节点j在n+1时刻的温度,℃;Fo为傅里叶准数;Δri为距离步长,m;Δτ为时间步长,s。
1.3.2对流边界节点温度的近似表达式
节点1为对流边界条件,其传热模型如图3所示,θ为所取区域范围的夹角,弧度。
根据能量守恒定律,节点1单元控制体积吸收的热量等于其增加的内能,则有
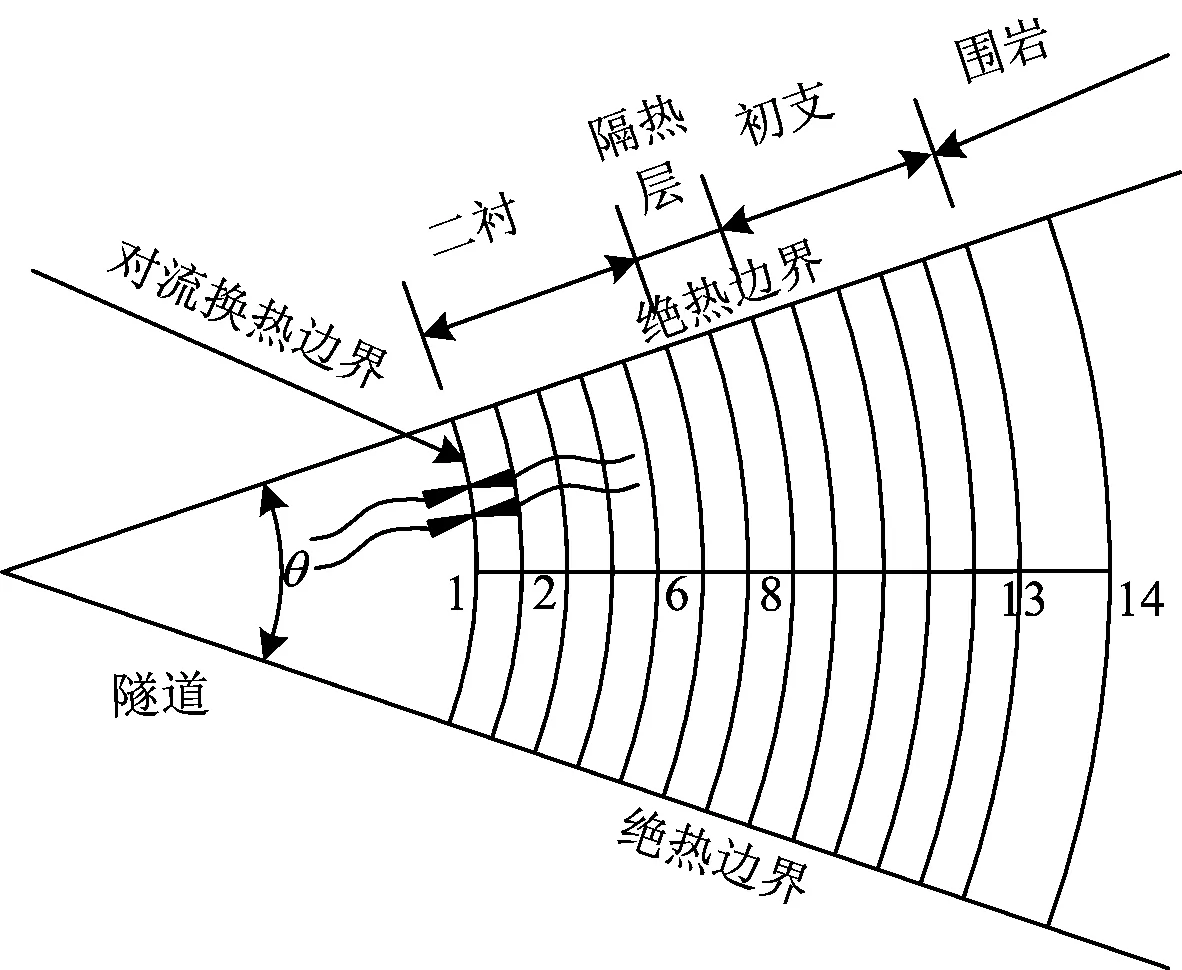
图3 对流换热模型
(4)
其中,
Qf-1=h(tf-t1,n)Rθ
式中:Qf-1为风流向对流边界的导热量;Q2-1为衬砌向对流边界的导热量;t1,n+1为节点1在n+1时刻的温度,℃;t1,n为节点1在n时刻的温度,℃;t2,n为节点2在n时刻的温度,℃。tf为风流温度,℃;h为对流换热系数,W·(m2·℃)-1。
整理式(4)可得对流边界节点1的温度t1,n+1近似计算式

(5)
其中,
式中:Bi为毕奥数。
1.3.3复合材料交界点处节点温度的近似表达式
节点两侧的距离步长、传热介质的热物性参数均不相同,其节点温度按能量守恒法推导。其传热模型如图4所示。
复合材料交界节点j所在的单元控制体积内包含了2种材料,对于非稳态问题,须求出ρcp项的当量值,其值可由下式给出。
(6)
其中,

图4 复合材料交界处传热模型
式中:u和v分别为单元控制体中介质1和2的体积;Δra为a种介质步长;Δrb为b种介质步长;rj为节点j距隧道中心的距离。
根据能量守恒定律可得

(7)
式中:Qa-j为介质a向节点j的导热量;Qb-j为介质b向节点j的导热量。
整理可得复合材料交界点处节点j(节点6、节点8、节点13)的温度tj,n+1的近似计算式为
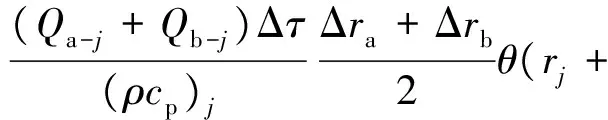
(8)
2 实例分析
2.1 温度实测断面和测点的选取
以牡绥线铁路改造工程中在建的绥阳隧道为例展开研究。绥阳隧道于2013年9月贯通,长度为6 170 m(DK491+549—DK497+719)。2015年1月对隧道内的风速、风向和温度场进行了实测。测试断面沿隧道纵向分布,自DK491+770起每隔250 m左右设置1个测试断面,每个测试断面内布置5个测点,其位置如图5所示。使用机械风表对隧道内的风速和风向进行了实测。测试结果为:绥阳隧道内的平均自然风速约为3.8 m·s-1,其值为隧道正中测点和隧道排水沟上部测点的平均值;风向都是自小里程端吹向大里程端。使用红外线测温仪GM1150对隧道断面二衬4个测点的温度进行实测,使用温度记录仪Testo174T对隧道保温侧沟的温度进行实测。

图5 隧道断面内测点分布图
2.2 计算参数的选取及温度场的计算
应用式(3)、式(5)和式(8)计算隧道贯通后的温度场。选择洞内距离小里程端洞口2 211 m(DK493+760)断面(简称为计算断面)上的温度进行分析。
根据当地的地层温度梯度3 ℃·(100 m)-1和隧道断面埋深得出计算断面上原始岩温tw=9.35 ℃。隧道断面的等效水力半径R′=2.5 m,即当量半径R=5 m。参考关于对流换热系数的实验研究[18],取对流换热系数h=15.9 W·(m2·℃)-1。断面各介质材料参数见表1。
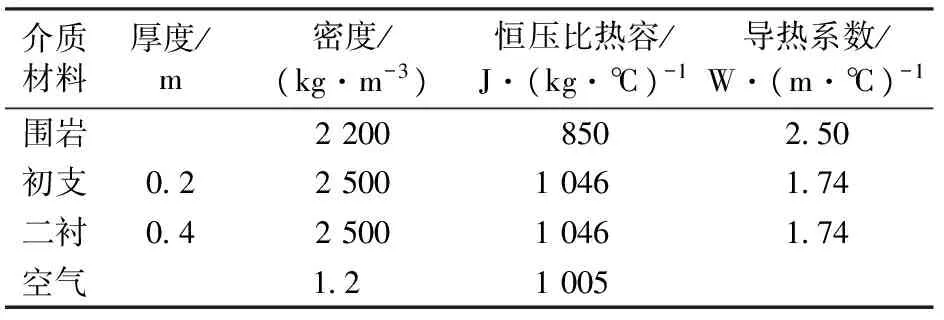
表1 介质材料参数
对绥阳隧道所在绥芬河地区自该隧道贯通时起至温度实测时止的气流温度进行统计分析,得出风流温度tf(℃)随时间i(自隧道贯通之日开始统计的天数)变化的关系,并根据实测隧道内气温对洞口风流温度随时间的变化函数进行修正,修正后的计算断面处风流温度的计算公式见式(9),可见风流温度变化曲线为正弦曲线。
(9)
在隔热层厚度为0(即无隔热层)的条件下,径向距离分别取5.0,5.6,12.6,22.6,32.6,42.6,52.6 m(其中,径向距离5.0 m对应于对流换热节点1,径向距离5.6 m对应于初支与围岩交界的节点,径向距离12.6~52.6 m分别对应于围岩内部的5个节点),计算自隧道贯通时起共24个月的隧道计算断面沿径向各点的各月平均温度随贯通时间的变化,如图6所示。
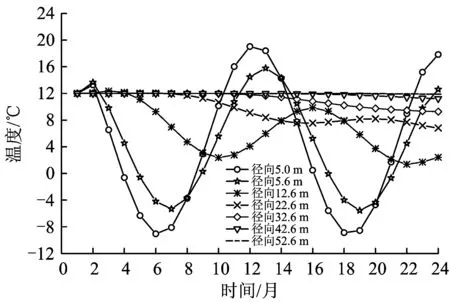
图6 隧道计算断面径向各点温度随贯通时间的变化曲线
由图6可知:隧道贯通后,随着时间的推移,距离衬砌表面一定范围内衬砌和围岩温度的变化曲线也为正弦曲线,与风流温度的相同;越往断面径向深处,温度的变化越小且相位滞后越大;随着径向深度的增加,围岩温度振幅(最高温与最低温之差)剧烈衰减,在r≈10R时,振幅衰减为0,深度继续增加,围岩温度不再随气流温度作周期性变化。
2.3 温度场的实测值与计算值的对比
在隧道贯通后第455天,计算断面上测点1到测点4的温度实测值分别为-8.300,-8.600,-8.675,-9.125 ℃,这4个测点的实测平均值为-8.675 ℃;保温侧沟测点的温度实测值为-5.080 ℃。此时计算断面的计算值(图2中的节点1)为-9.050 ℃,计算断面衬砌背后围岩(图2中的节点13)的温度计算值为-5.555 ℃。
对比计算断面的实测温度与计算温度可知:测点1(拱顶)的温度最高,测点4(轨面)的温度最低;从拱顶到轨面(测点1到测点4)的温度逐渐降低,且这4个测点的温度平均值与测点3(拱腰)的温度接近;温度的计算值低于4个测点的实测平均值约0.375 ℃,但满足工程使用精度要求;保温侧沟测点的温度高于4个测点的实测平均值约3.595 ℃,经查,与计算断面衬砌背后围岩温度接近,保温侧沟测点的温度高出计算断面衬砌背后围岩温度约0.475 ℃。
3 加设隔热层对温度场的影响
选用硬泡聚氨酯保温材料作为隔热材料,该材料的密度为ρ=370 kg·cm-3,恒压比热容为cp=1 500 J·(kg·℃)-1,导热系数为λ=0.021 5 W·(m·℃)-1。围岩初始温度取tw=12℃,参考隧道内最冷月平均温度选取恒定风温tf=-11.8 ℃。隔热材料分为2种铺设方式:中隔式(在初支和二衬之间),外贴式 (在二衬表面)。隔热层厚度分别取0(无隔热层),0.03, 0.05, 0.07, 0.09, 0.10 m。取连续30 d的计算断面温度进行分析,不同工况下隔热层对隧道二衬背后节点(图2中的节点6)温度场的影响如图7和图8所示。选取2种铺设方式中分别设置0.03和0.05 m厚隔热层后隧道二衬背后节点(图2中的节点6)的温度进行对比,如图9所示。

图7不同厚度的中隔式隔热层对隧道二衬背后节点温度的影响
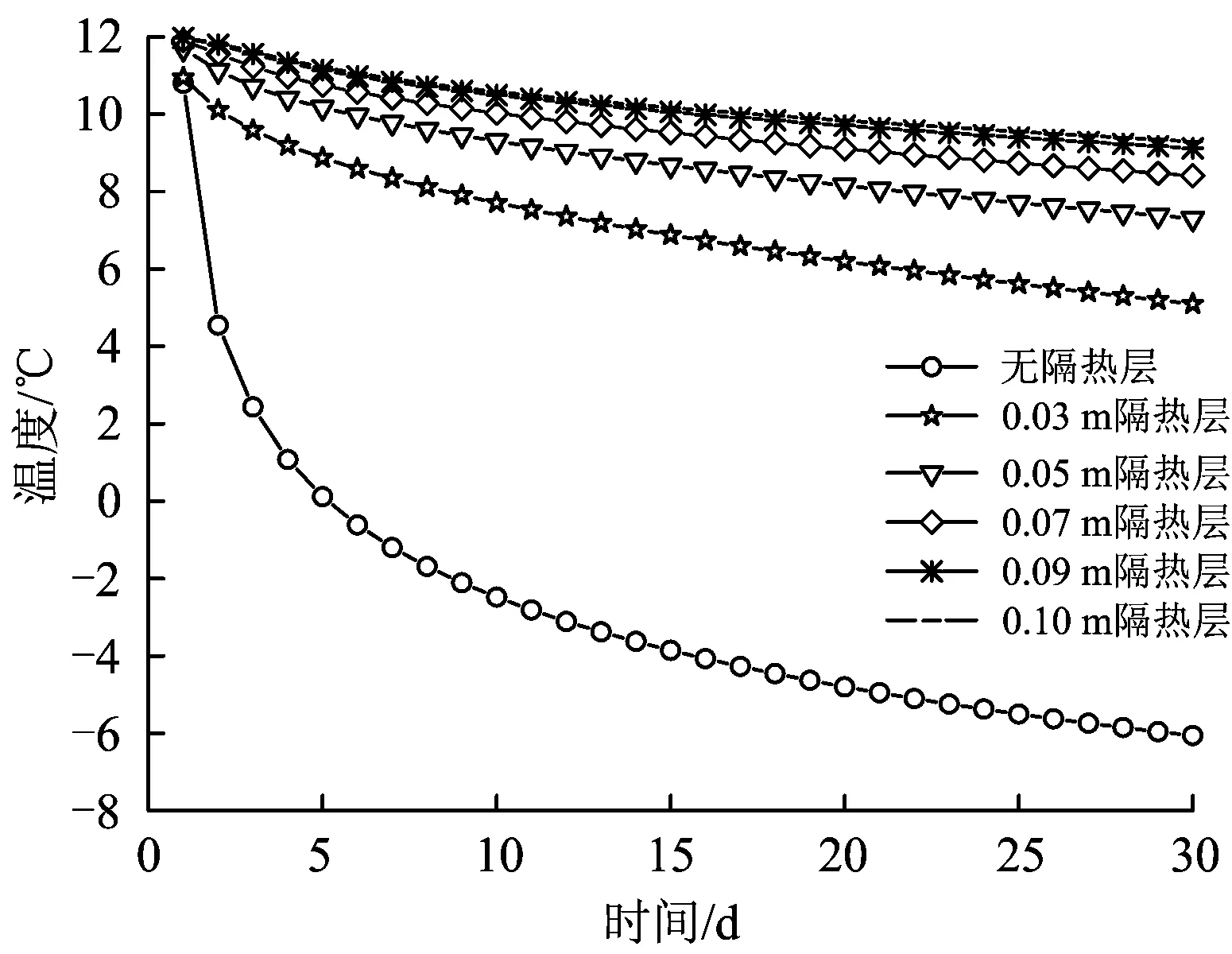
图8不同厚度的外贴式隔热层对隧道二衬背后节点温度的影响
由图7和图8可知:采用硬泡聚氨酯保温材料作为隔热层,可以有效提高寒区隧道衬砌和围岩温度;隔热层厚度越大,二衬背后初衬以及围岩的降温越慢;隔热层厚度为0.05 m左右时,工作效率最高;厚度大于0.07 m后,继续增加厚度所提升的保温效果不再显著,通过增加隔热层厚度来提高隧道衬砌和围岩温度的效果也是有限的。
如图9可知:外贴式和中隔式隔热层均能起到较好的保温效果;相比较而言,对于二衬背后节点温度,铺设0.03 m厚的隔热层时,外贴式比中隔式高0.36 ℃左右,铺设0.05 m厚的隔热层时,外贴式比中隔式高0.45 ℃左右,可见外贴式的保温效果更好。考虑到外贴式隔热层便于维护和更换,而中隔式隔热层遇水及受挤压均易变形,因此,在施工工艺允许的前提下,建议采用外贴式隔热层。
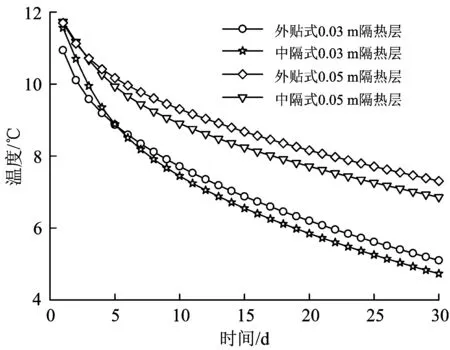
图9不同隔热层铺设方式及厚度对隧道二衬背后节点温度的影响
4 结 论
通过推导寒区隧道断面内非稳态热传导的有限差分方程,得到了隧道衬砌及围岩的温度场数值解,通过对寒区隧道温度场的计算和现场温度实测及保温隔热材料的分析,得到以下结论。
(1)隧道贯通后,随着时间的推移,距离衬砌表面一定范围内衬砌和围岩温度的变化曲线与风流温度的相同;往断面径向越深处,温度的变化越小且相位滞后越大;随着径向深度的增加,围岩温度振幅剧烈衰减,在r≈10R时,振幅衰减为0,深度继续增加,围岩温度不再随气温做周期性变化。
(2)隧道二衬拱顶处的温度最高,轨面处的温度最低,从拱顶到轨面的温度逐渐降低,各测点温度的平均值与拱腰处的温度接近;二衬温度的计算值稍低于实测平均值,但满足工程使用精度要求。保温侧沟处的温度与计算衬砌背后围岩温度接近。
(3)采用硬泡聚氨酯保温材料作为隔热层,可以有效提高寒区隧道衬砌和围岩温度。隔热层厚度为0.05 m左右时,工作效率最高;厚度大于0.07 m时,继续增加厚度所提升的保温效果不再显著。
(4)计算表明,外贴式和中隔式隔热层均能起到良好的保温效果,而外贴式的保温效果更优;同时,考虑到外贴式隔热层便于维护和更换,而中隔式隔热层遇水及受挤压均易变形,因此在材料及施工工艺允许的前提下,建议采用外贴式隔热层。
[1]乜风鸣. 寒冷地区铁路隧道气温状态[J]. 冰川冻土,1988,10(4):450-453.
(NIE Fengming. Dynamic State of Air Temperature in Railway Tunnel in Cold Regions[J]. Journal of Glaciology and Geocryology,1988,10(4):450-453. in Chinese)
[2]张先军. 青藏铁路昆仑山隧道洞内气温及地温分布特征现场试验研究[J]. 岩石力学与工程学报,2005,24(6):1086-1089.
(ZHANG Xianjun. Field Experiment on Distribution Characters of Air Temperature and Ground Temperature in Kunlunshan Tunnel of Qinghai—Tibet Railway[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(6):1086-1089. in Chinese)
[3]孙文昊. 寒区特长公路隧道抗防冻对策研究[D]. 成都:西南交通大学,2005.
(SUN Wenhao. Study on Frost-Resisting and Anti-Freezing Strategies of Extra-Long Highway Tunnel in Cold Area[D]. Chengdu:Southwest Jiaotong University,2005. in Chinese)
[4]陈建勋,罗彦斌. 寒冷地区隧道温度场的变化规律[J]. 交通运输工程学报,2008,8(2):44-48.
(CHEN Jianxun,LUO Yanbin. Changing Rules Temperature Field for Tunnel in Cold Area[J]. Journal of Traffic and Transportation Engineering,2008,8(2):44-48. in Chinese)
[5]赖金星,谢永利,李群善. 青沙山隧道地温场测试与分析[J]. 中国铁道科学. 2007,28(5): 78-82.
(LAI Jinxing, XIE Yongli, LI Qunshan. In-Situ Test and Analysis of the Ground Temperature Field in Qingshashan Highway Tunnel[J]. China Railway Science, 2007,28(5):78-82. in Chinese)
[6]张耀,何树生,李靖波. 寒区有隔热层的圆形隧道温度场解析解[J]. 冰川冻土,2009,31(1):113-118.
(ZHANG Yao,HE Shusheng,LI Jingbo. Analytic Solutions for Temperature Fields of a Circular Tunnel with Insulation Layer in Cold Region[J]. Journal of Glaciology and Geocryology,2009,31(1):113-118. in Chinese)
[7]张耀,赖远明,张学富. 寒区隧道隔热层设计参数的实用计算方法[J]. 中国铁道科学, 2009, 30(2): 66-70.
(ZHANG Yao, LAI Yuanming, ZHANG Xuefu. A Practical Method for Calculating the Design Parameters of the Heat Insulation Layer in Cold Region Tunnel[J]. China Railway Science, 2009, 30(2): 66-70. in Chinese)
[8]肖琳,杨成奎,胡增辉,等. 地铁隧道围岩内温度分布规律的模型试验及其热导率反算研究[J]. 岩土力学,2010,31(增刊2):86-91.
(XIAO Lin,YANG Chengkui,HU Zenghui,et al. Model Test on Temperature Distribution in Metro Tunnel Surrounding Rock and Inverse Calculation of Its Thermal Conductivity[J]. Rock and Soil Mechanics,2010,31(Supplement 2):86-91. in Chinese)
[9]KRARTI M,KREIDER J F.Analytical Model for Heat Transfer in an Underground Air Tunnel[J]. Energy Conversion and Management,1995,37(10):1561-1574.
[10]LAI Y M, LIU S Y, WU Z W,et al. Approximate Analytical Solution for Temperature Fields in Cold Regions Circular Tunnels[J]. Cold Regions Science and Technology,2002,34:43-49.
[11]PRASHANT K J,SUNEET S,RIZWAN-UDDIN. Analytical Solution to Transient Asymmetric Heat Conduction in a Multilayer Annulus[J]. Journal of Heat Transfer,2009,131(1):1-7.
[12]SUNEET S,PRASHANT K J,RIZWAN-UDDIN. Analytical Solution to Transient Heat Conduction in Polar Coordinates with Multiple Layers in Radial Direction[J]. International Journal of Thermal Sciences,2008,47:261-273.
[13]夏才初,张国柱,肖素光.考虑衬砌和隔热层的寒区隧道温度场解析解[J].岩石力学与工程学报,2010,29(9):1767-1773.
(XIA Caichu,ZHANG Guozhu,XIAO Suguang. Analytical Solution to Temperature Fields of Tunnel in Cold Region Considering Lining and Insulation Layer[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(9):1767-1773. in Chinese)
[14]陈功胜. 巷道围岩调热圈半径及温度场分布规律研究[J]. 煤炭技术,2014,33(4):113-115.
(CHEN Gongsheng. Study on Cooled Zone Radius and Temperature Distribution Law of Surrounding Rock[J]. Coal Technology,2014,33(4):113-115. in Chinese)
[15]江亦元,王星华. 昆仑山隧道渗漏水原因探讨及治理[J]. 中国铁道科学, 2005, 26(4): 52-56.
(JIANG Yiyuan, WANG Xinghua. Study on Waterproof Treatment and Causes for Leakage Water of Kunlun Mountain Tunnel[J]. China Railway Science, 2005, 26(4): 52-56. in Chinese)
[16]王引生,贾海锋. 青藏铁路昆仑山隧道排水侧沟模型试验研究[J]. 中国铁道科学, 2006,27(1): 28-31.
(WANG Yinsheng, JIA Haifeng. Model Test and Study on the Drainage Side Ditch of Kunlunshan Tunnel on Qinghai—Tibet Railway[J]. China Railway Science, 2006, 27(1): 28-31. in Chinese)
[17]俞佐平. 传热学[M]. 第2版. 北京:高等教育出版社,1985.
(YU Zuoping. Heat Trasfer[M]. 2nd ed. Beijing:Higher Education Press, 1985. in Chinese)
[18]张建荣,刘照球. 混凝土对流换热系数的风洞实验研究[J]. 土木工程学报, 2006,39(9): 39-42.
(ZHANG Jianrong, LIU Zhaoqiu. A Study on the Convective Heat Transfer Coefficient of Concrete in Wind Tunnel Experiment[J]. China Civil Engineering Journal,2006,39(9): 39-42. in Chinese)
