考虑车底接续延误概率的普速旅客列车车底套用方案鲁棒优化

朱昌锋，李引珍

(兰州交通大学 交通运输学院，甘肃 兰州　730070)

旅客列车车底是完成客运生产任务的重要移动装备，在铁路装备投资中占有较大的比重。合理的车底运用方案可减少车底投入数量，降低运营成本，因此，优化车底运用对于提高铁路运输生产效益具有重要意义。

车底套用是提高车底运用效率的有效途径之一，为此，相关学者就该问题开展了大量的研究，并取得了一定的研究成果。聂磊等[1]、赵鹏等[2]、史峰等[3]、张才春等[4]从不同角度研究了动车组运用计划的优化模型，对普速旅客列车车底运用具有一定的参考价值，但由于普速旅客列车车底类型及其编组结构的多样性，对其运用优化具有一定的挑战。Cordeau等[5]运用Benders分解法研究了机车和车底调用；刘钢等[6]建立了普速旅客列车车底周转接续的双层指派优化模型，但仅考虑了同等级列车之间车底的接续以及始发列车的车底属于同一路局的情况；谢金贵等[7]利用多商品网络流理论，建立了普速旅客列车车底运用优化的整数规划模型，但由于该问题属于NP问题，需寻找更加有效的求解算法；肖益帆等[8]通过考虑不同等级列车间的车底套用，建立了以所需车底数量最少为目标的普速旅客列车车底运用优化模型，设计了基于模拟退火算法的求解策略；Zeyi BING[9]通过引入“列车串”，建立了以车底在始发站和终到站停留时间最少为目标的普速旅客列车车底运用优化模型；朱昌锋等[10-11]以始发和终到旅客列车的车底不必要在站停留时间最少为目标函数，建立基于既定运行详图的普速旅客列车车底套用优化模型，分析了车底套用对铁路大型客运站到发线分配的影响。上述研究从不同的视角对该问题进行了研究，但仅研究了任一普速旅客列车车底最多可套跑1个区段的套用模式，且未能考虑列车晚点对车底套用的扰动影响以及车底运用的均衡性，使得所建优化模型具有一定的局限性，限制了优化模型的实际应用效果。

基于此，本文在不改变普速旅客列车车底配属制的前提下，通过考虑列车晚点对车底套用的扰动影响以及车底运用的均衡性，提出考虑车底接续延误概率的普速旅客列车车底套用方案鲁棒优化模型，设计基于Pareto排序的多目标粒子群优化算法(Multi-objective particle swarm optimizer，MOPSO)，进一步提高普速旅客列车车底套用的效率和鲁棒性。

1　问题描述及分析

根据铁路路网布局及列车运行图，设Z={ze|e=1,2,…,E}为铁路列车运行图中有普速旅客列车始发和终到的客运站集合；S={sf|f=1,2,…,F}为普速旅客列车车底集合；L={li|i=1,2,…,I}为路网上所有普速旅客列车的运行线集合，La={lai|i=1,2,…,Ia}为终到任一客运站ze的普速旅客列车运行线集合，Ld={ldj|j=1,2,…,Jd}为由任一客运站ze始发的普速旅客列车运行线集合，一般情况下，La=Ld；tai为任一普速旅客列车运行线lai的图定终到时刻，tdj为任一普速旅客列车运行线ldj的图定始发时刻。

“长途套跑短途”的普速旅客列车车底套用模式[8-10]如图1所示，即通过利用任一长途普速旅客列车lai的车底在客运站ze的非生产停留时间，使该车底套跑短途列车对ldj和lai′(lai′∈La)。

图1　“长途套跑短途”的普速旅客列车车底套用模式

由图1可见，该类普速旅客列车车底套用模式其实就是通过优化普速旅客列车车底的周转接续，使终到配属站(折返站)的车底，在满足车底整备作业时间等约束的前提下，能够担当另一普速旅客列车对的运行任务，并尽可能地减小车底在配属站(折返站)的停留时间。但是该类车底套用模式受到以下两方面硬约束的限制。

(1)车底仅可在1个主跑区段(z1-ze)和1个套跑区段(ze-z2)间运行，长途普速旅客列车在主跑区段(z1-ze)间运行，短途普速旅客列车在套跑区段(ze-z2)间运行。

(2)短途普速旅客列车lai′的车底必须于长途普速旅客列车ldj′在ze站的图定发车时刻之前返回ze站。

由于上述两方面的硬约束，使得1个车底最多只能套跑1个区段，限制了满足套用条件的普速旅客列车数量，难以有效提高车底套用的效率。

为了进一步提高普速旅客列车车底套用的效率，在满足车底必要接续时间的基础上，取消上述两方面的限制，使任一车底连续承担多条普速旅客列车运行线的运行任务后再返回配属站，此时，这些普速旅客列车运行线便构成1个车底套用的大循环，可进一步节省车底数和客技站的投资规模。但由于不同旅客列车运行线之间具有一定的关联性，任一车底接续的延误将影响整个车底的周转秩序和相关列车的运行秩序，也直接影响着车底套用方案的兑现，因此，鲁棒性是车底套用优化中必须考虑的一个关键问题。

由此可见，该问题可转化为：在满足普速旅客列车车底必要接续时间等相关约束的基础上，通过考虑车底接续的延误概率，优化得到能满足一定条件的若干个车底接续关系的集合。

2　列车晚点时间和车底接续时间对车底接续延误概率的影响

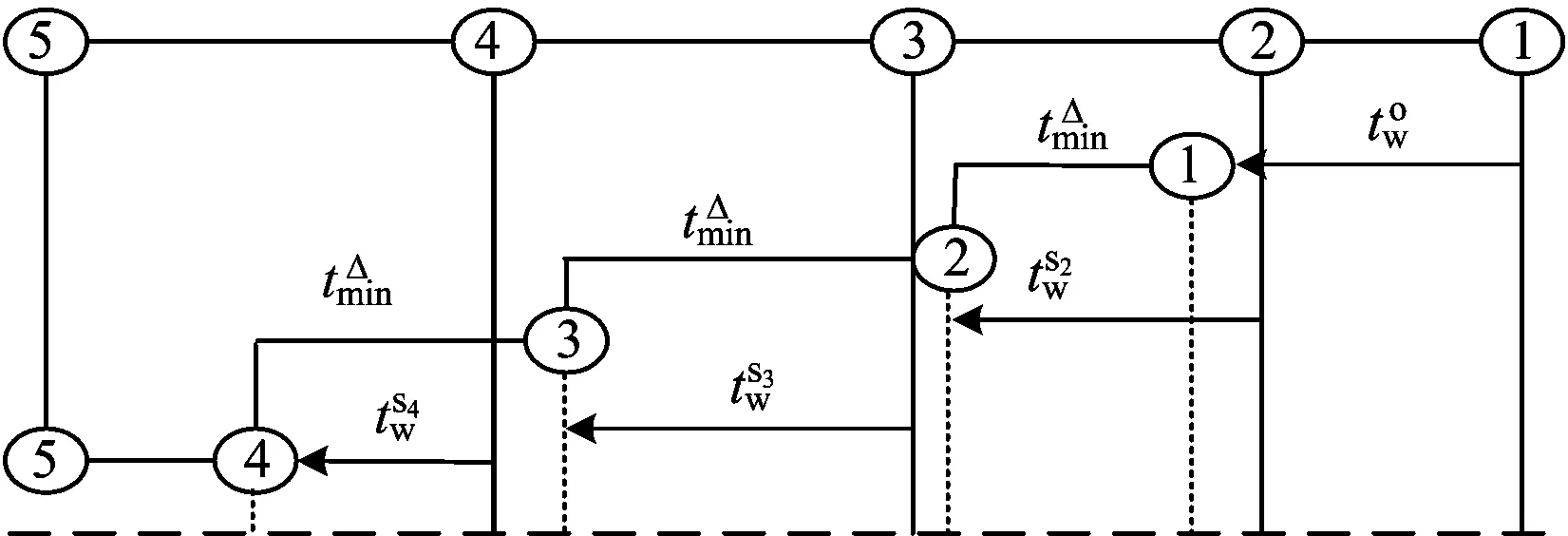
图2　列车终到晚点传播

图3　列车始发晚点传播

设tw为旅客列车晚点时间；toper为旅客列车在客运站的技术作业时间；tr为运行图区间容差；thc为车站预留的缓冲时间，tcon为车底接续时间。列车晚点对车底接续延误的影响分析如图4所示。

当列车晚点时间tw小于车站预留的缓冲时间thc或车底接续时间tcon较大时(见图4(a))，列车晚点不影响车底接续；当列车晚点时间tw大于车站预留的缓冲时间thc或车底接续时间tcon较小时(见图4(b))，列车晚点将影响车底接续，但由于存在车站预留的缓冲时间thc和运行图区间容差tr，可采取“赶点”等间隔动态小幅度调整措施，因此仅会影响部分车底的接续；当列车晚点时间tw继续增大或车底接续时间tcon较小时，如果综合利用车站预留的缓冲时间thc和运行图区间容差tr，列车晚点仍不能得到缓解(见图4(c))，使得套用模式下的车底接续难以满足要求，就需大幅度调整予以解决。由此可见，列车晚点时间越小或车底接续时间越大，车底接续延误概率越小；反之，列车晚点时间越大或车底接续时间越小，车底接续延误概率越大。

图4　列车晚点对车底接续延误的影响分析

(1)

(2)

式中：λtw为继发晚点平均时间的倒数。

(3)

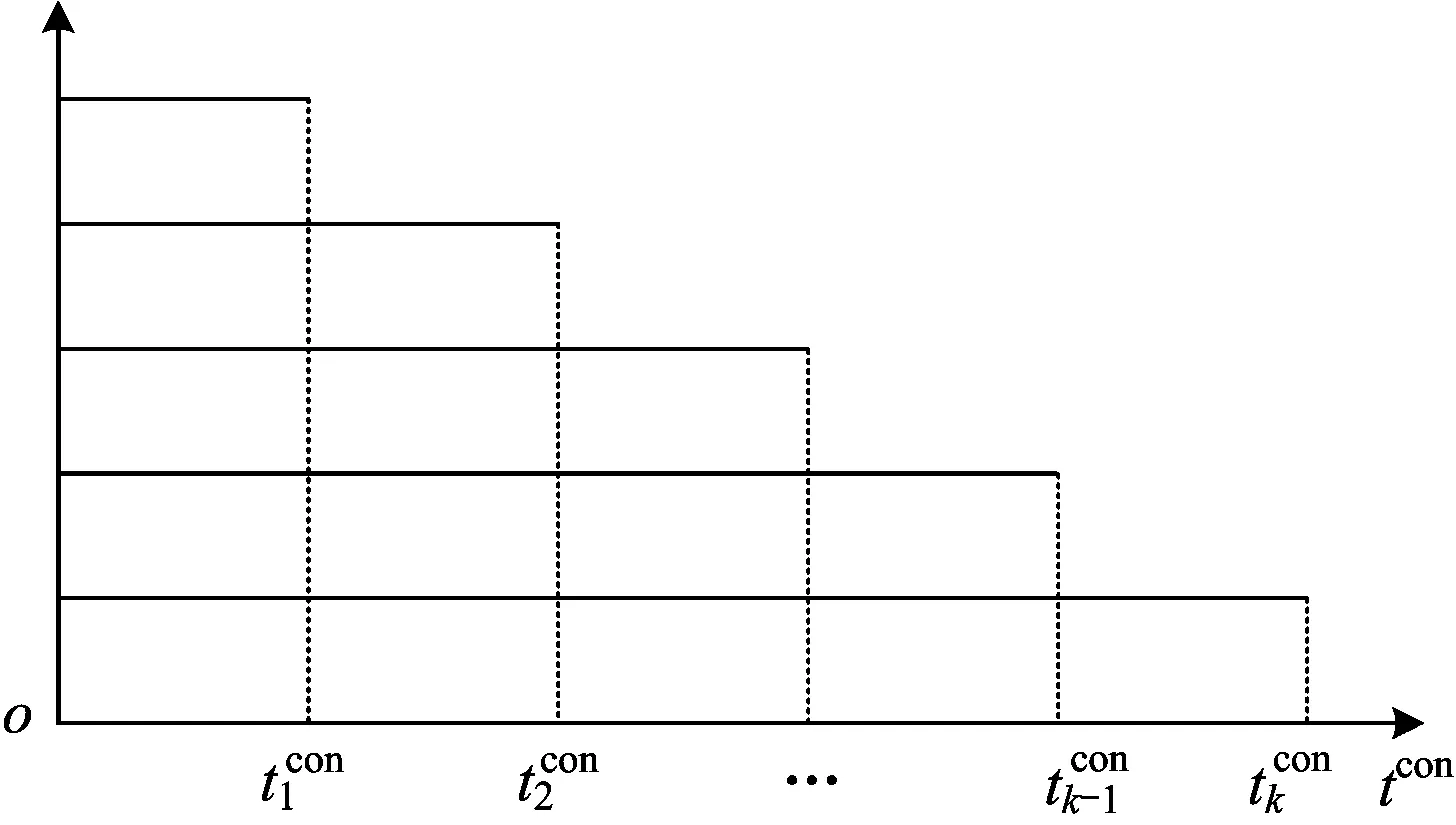
图5　车底接续时间与车底接续延误概率间的关系

3　优化模型

3.1　约束条件

(1)车底接续的唯一性约束。根据既定铁路列车运行图，在任一运行周期内，任一普速旅客列车lai的车底到达终到站后，最多只能接续1个在该客运站始发的后续车次ldj的运行任务，如果在该周期内无法接续套用，只能转入下一运行周期。同理，在任一运行周期内，任一始发普速旅客列车ldj的车底只能由任一终到的普速旅客列车lai提供。车底终到与始发接续在同一运行周期内如图6所示，车底终到与始发接续不在同一运行周期内如图7所示。

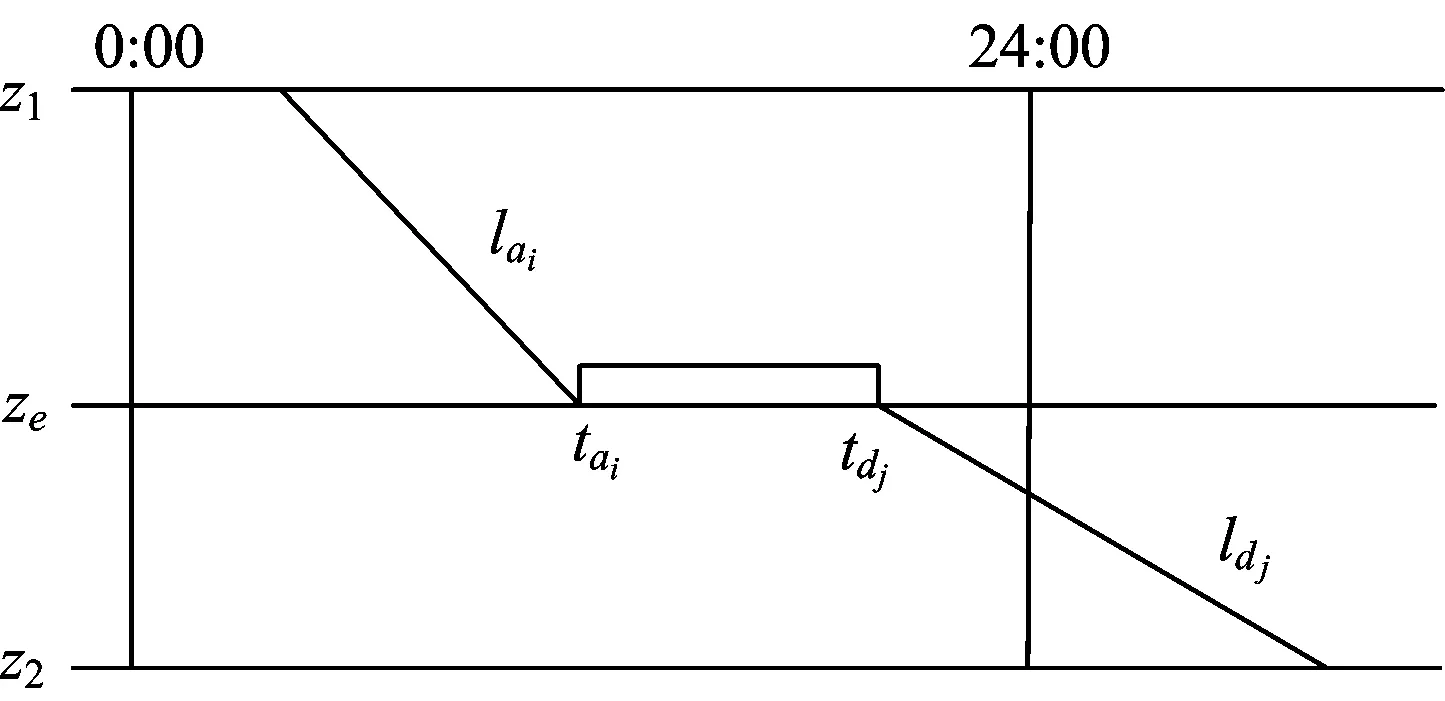
图6　车底终到与始发接续在同一运行周期内

图7　车底终到与始发接续不在同一运行周期

定义Xij为0-1变量，表示若普速旅客列车lai的车底接续ldj的运行任务，则Xij=1，否则Xij=0。由此得到车底接续的唯一性约束可表示为

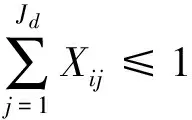
(4)

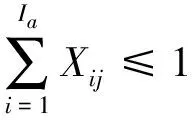
(5)

(2)车底接续地点约束。只有当任一普速旅客列车ldj的始发站zdj与任一普速旅客列车lai的终到站zai为同一客运站时，普速旅客列车lai的车底才有可能承担普速旅客列车ldj的运行任务，即

zai=zdj

(6)

(3)车底接续时刻约束。在任一运行周期内，普速旅客列车ldj的始发时刻必须晚于普速旅客列车lai的终到时刻，同时，还应保证必要的列车到发、车底整备等作业时间。

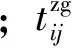
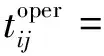
(7)

其中，

式中：ζij为0-1变量，当普速旅客列车lai的车底在接续普速旅客列车ldj前需进整备所整备时，则ζij=1，否则ζij=0；ϑij为0-1变量，当普速旅客列车lai的车底需转股道接续普速旅客列车ldj时，则ϑij=1，否则ϑij=0。

因此普速旅客列车lai的车底接续普速旅客列车ldj的时刻应满足

(8)

此时，车底在始发站(终到站)的非生产停留时间tij为

(9)

其中，

(4)车底的匹配度约束。被套用车底与套用列车之间在到发接续时间间隔、车底要求(设计速度、编组结构等)方面应有尽可能高的匹配度。

设wij为普速旅客列车lai的车底接续ldj的时间匹配度，其值越小则接续套跑的可能性越大，反之则越小。则不考虑车底接续延误概率的接续时间匹配度为

(10)

而考虑车底接续延误概率的接续时间匹配度为

(11)

设φij为普速旅客列车lai和ldj的车底在设计速度、编组结构等方面的匹配度，其值越小则接续套跑的可能性越大，反之则越小，即

(12)

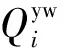
(13)

(14)

(5)车底日常检修约束。任一普速旅客列车车底sf在接续套跑的过程中，应满足检修的时间间隔、走行公里的约束，二者只要有1个条件满足，即应安排该车底进行检修。

(15)

(6)车底运用的唯一性约束。在任一运行周期内，铁路列车运行图规定的任一普速旅客列车运行线li有且仅有1个车底来承担其运行任务，即

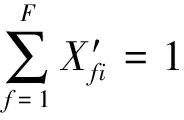
(16)

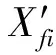
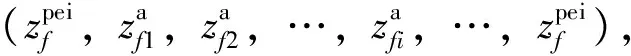
(17)

(8)车底接续时间的控制约束。在提高车底套用方案鲁棒性(抗干扰能力)的过程中，不能以无限延长车底接续的非生产停留时间为代价，需将车底接续的非生产停留时间控制在一定的范围之内，即

(18)

式中：r为鲁棒性因子，0≤r≤1；Copt为不考虑车底接续延误概率时，所有车底接续的非生产停留时间总和的最小值。

3.2　目标函数

为了提高车底套用方案的鲁棒性(抗干扰能力)，以车底接续延误概率最小为目标函数1，即

(19)

为了尽可能达到普速旅客列车车底运用的均衡性，以车底运用效率的标准差最小为目标函数2，即

(20)

其中，

4　算法设计

普速旅客列车车底套用方案鲁棒性优化模型的约束条件众多，且同时存在等式和不等式约束，2个目标函数间还存在很强的相关性，因此，必须采用高效的多目标算法进行求解。粒子群算法(Particle Swarm Optimization algorithm，PSO)是一种随机搜索、并行的优化算法，可将非劣最优解集Pareto 排序机制和传统的PSO算法结合，求解多目标优化问题。

传统的PSO算法中，粒子在搜索过程中按如下公式进行更新[16]

(21)

(22)

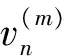
但传统的PSO算法在求解多目标问题时，存在惯性权重θ的取值缺乏依据以及非劣最优解集Pareto的多样性、分布性较差等问题。为此，本文基于非劣最优解集Pareto排序的多目标粒子群算法(Multi-objective particle swarm optimizer，MOPSO)，对惯性权重θ的取值和非劣解集Pareto更新策略进行如下改进。

1)自适应惯性权重的取值依据

本文根据粒子与种群最优粒子的差距程度，非线性地调整惯性权重的大小，即[17]

(23)

(24)

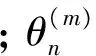
自适应惯性权重曲线如图8所示。

图8　自适应惯性权重曲线

2)基于动态密集距离的非劣解集更新策略

任一粒子与其周围粒子间的动态密集距离表述为

(25)

为保证 Pareto 解集中解的多样性和均匀性，从动态密集距离Y(xn)较大的前20%个Pareto解中随机选出种群全局最优解[18]，用于指导种群的更新。算法流程如图9所示。

5　实例分析

以旅客列车到发较为密集的北京西、郑州、西安、兰州4个铁路大型客运站为例，随机选取不同等级的20个车次，并对其信息进行格式化，结果见表1。

非套用模式下，车底在配属站或折返站停留时间大于10 h的有16个，大于20 h的有3个，最大停留时间为1 417 min，需要22个车底。

取旅客乘降的期望时间为5 min；清扫检查的期望时间为15 min；进出整备所及在整备所非整备维修的期望时间为20 min；转股道所需的期望时间为10 min；车底检修作业时间标准、维修时间间隔、走行公里依据《铁路客车运用维修规程》取值。

结合文献[12,14]的研究，以30 min为1个时间段，列车晚点时间在[0,30]，(30,60]，(60,90]，(90,120]，(120,150]各时间段内的概率分别取0.25，0.15，0.10，0.05，0.05，晚点150 min以上的概率取0.05。采用本文提出的模型和优化算法，计算得到的考虑车底接续延误概率的普速旅客列车车底套用方案见表2。

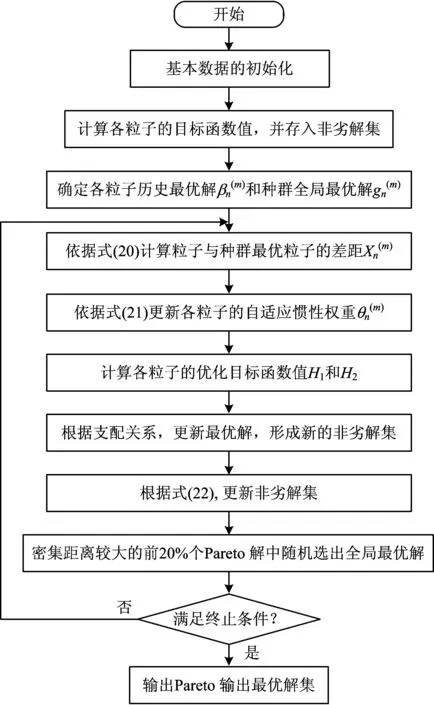
图9　算法流程

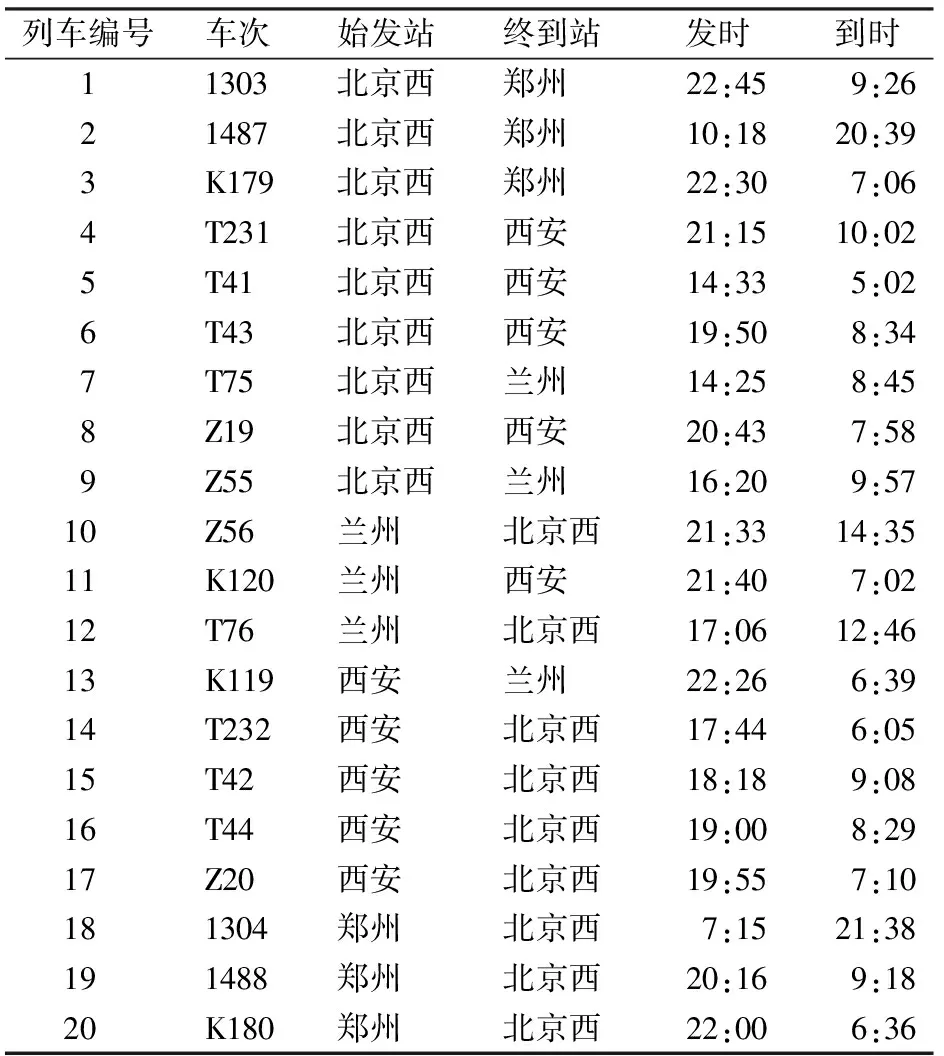
列车编号车次始发站终到站发时到时11303北京西郑州　22：459：2621487北京西郑州　10：1820：393K179北京西郑州　22：307：064T231北京西西安　21：1510：025T41北京西西安　14：335：026T43北京西西安　19：508：347T75北京西兰州　14：258：458Z19北京西西安　20：437：589Z55北京西兰州　16：209：5710Z56兰州　北京西21：3314：3511K120兰州　西安　21：407：0212T76兰州　北京西17：0612：4613K119西安　兰州　22：266：3914T232西安　北京西17：446：0515T42西安　北京西18：189：0816T44西安　北京西19：008：2917Z20西安　北京西19：557：10181304郑州　北京西7：1521：38191488郑州　北京西20：169：1820K180郑州　北京西22：006：36

由表2可见：考虑车底接续延误概率的4个套用方案中，每个套用方案均只用5个车底接续循环就覆盖了所有车次；车底在配属站和折返站的最小、最大总停留时间分别为8 917和9 293 min，每个套用方案所需的车底数均为19个；与现行非套用模式下的车底运用相比较，考虑车底接续延误概率的套用方案可节省的最小、最大停留时间分别为3 964和4 340 min，每个套用方案均可节省3个车底。

为了进一步分析本文所建模型的合理性，对考虑车底接续延误概率和不考虑车底接续延误概率两种情况下的套用方案进行对比分析。参照不考虑车底接续延误概率条件下的套用模型[10]，计算得到不考虑车底接续延误概率的套用方案见表3。

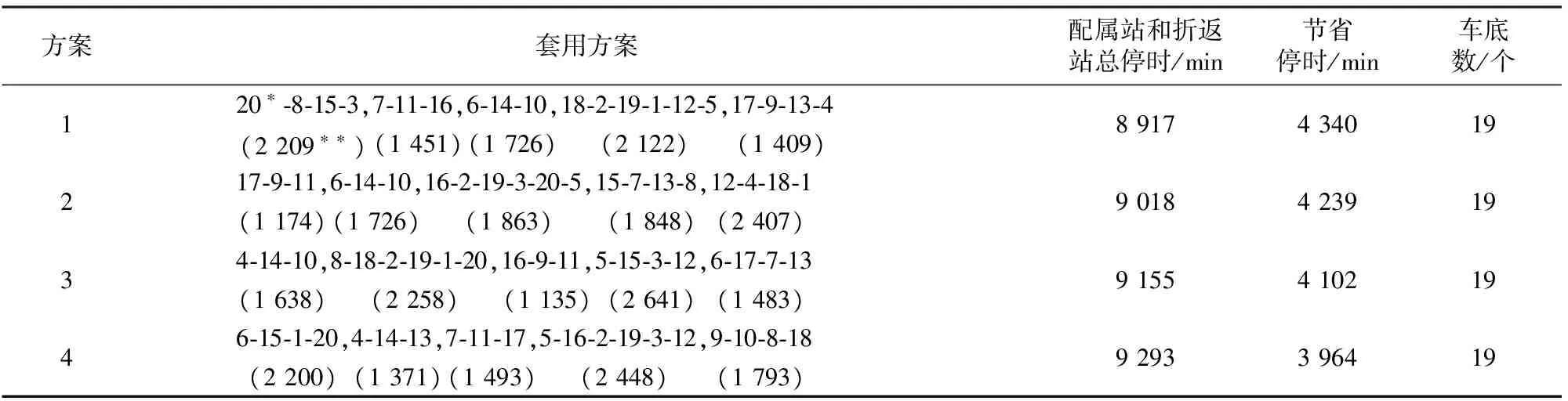
表2　考虑车底接续延误概率的套用方案

注：*为列车编号；**为该接续循环内车底在配属站和折返站的总停留时间， min。

表3　不考虑车底接续延误概率的套用方案

对比表2和表3可见：考虑车底接续延误概率和不考虑车底接续延误概率2种情况下，套用方案所需的车底数均为19个，但不考虑车底接续延误概率条件下，车底在配属站和折返站的最小总停时为8 307 min，而考虑车底接续延误概率条件下的最小总停时为8 917 min。这2种情况下车底总停时最小的套用方案分别如图10、图11所示。

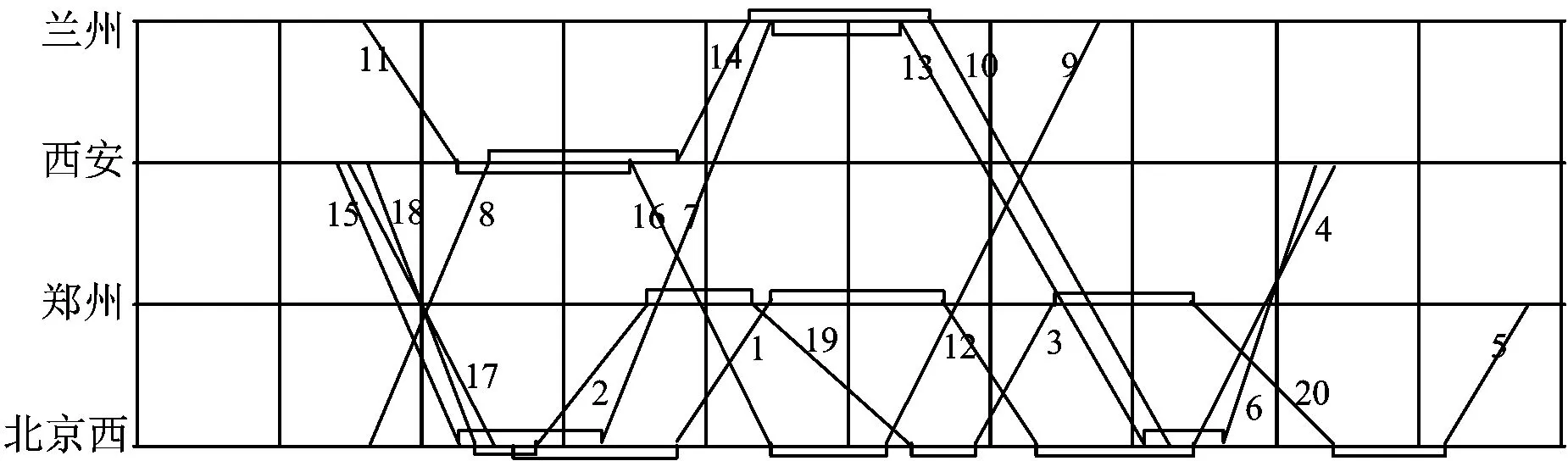
图10不考虑车底接续延误概率条件下总停时最小的套用方案1′

由图10可见：在不考虑车底接续延误概率条件下总停时最小的套用方案1′中，最小车底接续时间仅为42 min(编号19的列车车底接续编号3的列车)，极易产生车底接续延误，方案的鲁棒性较差。

图11考虑车底接续延误概率条件下总停时最小的套用方案1

由图11可见：在考虑车底接续延误概率条件下总停时最小的套用方案1中，最小车底接续时间为67 min(编号19的列车车底接续编号1的列车)，方案的鲁棒性较好。

6　模型讨论与分析

(1)在处理列车晚点时间概率时，本文对时间段的划分及其晚点时间概率的取值相对粗略。在实际铁路运输组织中，可根据不同时期列车晚点的差异性，采取更合理的动态划分方法及其取值标准。

(2)铁路客运枢纽是旅客列车密集始发、终到的场所，也是解决普速旅客列车车底套用的关键环节。对于有多个客运站的铁路客运枢纽，可采取以下策略进一步提高套用效率。

①可通过调整旅客列车在客运枢纽内的始发站、终到站，进一步提高普速旅客列车车底套用的效率。但该策略需调整列车运行图，应在调图前予以研究。

②可将有多个客运站的铁路大型客运枢纽看作为1个点(1个客运站)，终到该枢纽内所有客运站的车底可统一重新分配利用。该策略无需调整列车运行图，但需将部分车底进行枢纽内站间调整。此时，本文所建模型中的zai(zdj)可能是某客运站，也可能是有多个客运站的客运枢纽。客运枢纽内站间车底调整如图12所示。

7　结　语

普速旅客列车车底运用方式的优化对提高铁路客运生产效益和效率具有重要的意义。本文在不改变车底配属制的前提下，提出1个车底可套跑多个区段的普速旅客列车车底运用模式；分析了车底接续时间与车底接续延误概率间的关系，提出了考虑车底接续延误概率的普速旅客列车车底套用方案鲁棒优化模型及其优化算法。通过实例，对非套用模式、不考虑车底接续延误概率的套用模式和考虑车底接续延误概率的套用模式3种情况下的普速旅客列车车底套用方案进行了比较分析。研究结果表明：考虑车底接续延误概率的普速旅客列车车底套用方案鲁棒优化模型，不但可提高车底的运用效率，也具有一定的鲁棒性。但为了进一步挖掘普速旅客列车车底运用的潜能，应研究编图前的普速旅客列车车底经济合理运用问题，以及套用条件下的乘务组合理调配问题，以期为铁路普速旅客列车车底运用优化提供决策依据，这将是后续研究的重点问题。

图12　客运枢纽内站间车底调整

[1]聂磊，赵鹏，杨浩，等.高速铁路动车组运用的研究[J].铁道学报，2001，23(3)：1-7.

(NIE Lei，ZHAO Peng，YANG Hao，et al. Study on Motor Trainset Operation in High Speed Railway[J]. Journal of the China Railway Society，2001，23(3)：1-7.in Chinese)

[2]赵鹏，富井规雄. 基于概率局域搜索的动车组平日运用计划编制算法[J].系统工程理论与实践，2004(2)：123-129，144.

(ZHAO Peng，NORIO Tomii. An Algorithm for Train-Set Scheduling on Weekday Based on Probabilistic Local Search[J]. Systems Engineering—Theory & Practice，2004(2)：123-129，144. in Chinese)

[3]史峰，周文梁，郁宇卫，等.客运专线动车组运用计划优化模型与算法[J].铁道学报，2011，33(1)：1-13.

(SHI Feng，ZHOU Wenliang，YU Yuwei，et al.Optimized Model and Algorithm of Motor Train-Sets Scheduling for Dedicated Passenger Lines[J]. Journal of the China Railway Society，2011，33(1)：1-13. in Chinese)

[4]张才春，花伟，陈建华. 双修制下的动车组运用计划编制研究[J].铁道学报，2010，32(3)：16-19.

(ZHANG Caichun，HUA Wei，CHEN Jianhua. Research on EMU Scheduling under Constraint of Kilometrage and Time for Scheduled Inspection and Maintenance[J]. Journal of the China Railway Society，2010，32(3)：16-19. in Chinese)

[5]CORDEAU J F，SOUMIS F，DESROSIERS J. Simultaneous Assignment of Locomotives and Cars to Passenger Trains[J].Operations Research, 2001，49 (4)：531-548.

[6]刘钢，孙晚华，韩学雷.旅客列车车底运用优化模型及算法[J].铁道运输与经济，2004，26(2)：62-64.

(LIU Gang，SUN Wanhua，HAN Xuelei. An Optimized Model and Algorithm for the Utilization of Passenger Carriage [J].Railway Transport and Economy，2004，26(2)：62-64. in Chinese)

[7]谢金贵，曾亮，徐昕恺.铁路旅客列车车底套用优化模型的研究[J].铁道运输与经济，2006，28(12)：75-77.

(XIE Jingui，ZENG Liang，XU Xinkai. Study on Optimization Model of Railway Passenger Train Set Assignment [J]. Railway Transport and Economy，2006，28(12)：75-77. in Chinese)

[8]肖益帆，朱昌锋.基于模拟退火算法的铁路旅客列车车底套用优化研究[J]. 铁道科学与工程学报，2012，9(5)：108-113.

(XIAO Yifan，ZHU Changfeng.Railway Train Set Assignment Based on Simulated Annealing Algorithm[J].Journal of Railway Science and Engineering，2012，9(5)：108-113. in Chinese)

[9]BING Zeyi， LI Wentian， ZHU Changfeng，et al. Research on Assignment Optimization of Railway Train Stock Based on Simulated Annealing Algorithm [J]. Journal of Information and Computational Science，2014，11(14)：4911-4919.

[10]朱昌锋，李引珍.基于既定列车运行图的铁路旅客列车车底套用协同优化研究[J]. 中国铁道科学，2014，35(3)：120-128.

(ZHU Changfeng，LI Yinzhen. Collaborative Optimization on Assignment of Passenger Train Stock Based on Given Train Diagram [J]. China Railway Science，2014，35(3)：120-128.in Chinese)

[11]朱昌锋. 铁路大型客运站到发线分配耦合优化及时域调整研究[D].兰州：兰州交通大学，2014.

(ZHU Changfeng. Research on Coupling Optimization of Arrival and Departure Track Scheduling for Railway Large-Scale Passenger Station and Its Receding Horizon Adjustment[D].Lanzhou：Lanzhou Jiaotong University，2014.in Chinese)

[12]宗俊雅，李宗平. 列车运行图缓冲时间合理取值究[J]. 交通运输工程与信息学报，2010，8(3)：56-61.

(ZONG Junya，LI Zongping. Study on Reasonable Value of the Buffer Time in Train Diagram [J]. Journal of Transportation Engineering and Information，2010，8(3)：56-61.in Chinese)

[13]胡思继，孙全欣，胡锦云，等. 区段内列车晚点传播理论的研究[J]. 中国铁道科学，1994，15(2)：41-53.

(HU Siji，SUN Quanxin，HU Jinyun，et al. Research on Theories of Train Delay Propagation in a Railway District [J]. China Railway Science，1994，15(2)：41-53. in Chinese)

[14]孙焰，刘胤宏，李致中，等.列车运行图的晚点概率分析[J].长沙铁道学院学报，1998，16(4)：83-89.

(SUN Yan，LIU Yinhong，LI Zhizhong，et al.The Analysis of Delaying Time Probability for the Travelling Graph of Trains[J]. Journal of Changsha Railway University，1998，16(4)：83-89. in Chinese)

[15]彭其渊，朱松年，阎海峰. 列车运行图可调整度评价系统研究[J].西南交通大学学报，1998，33(4)：367-371.

(PENG Qiyuan，ZHU Songnian，YAN Haifeng.A System for Evaluation of Train Diagram Elasticity [J].Journal of Southwest Jiaotong University，1998，33(4)：367-371.in Chinese)

[16]贾兆红，陈华平，唐俊，等. 面向多目标的自适应动态概率粒子群优化算法[J]. 系统仿真学报，2008，20(18)：4959-4963.

(JIA Zhaohong，CHEN Huaping，TANG Jun，et al. Self-Adaptive Dynamic Probabilistic Particle Swarm Optimization Algorithm for Multiple Objectives[J].Journal of System Simulation，2008，20(18)：4959-4963.in Chinese)

[17]HO S L，YANG Shiyou，NI Guangzheng，et al. A Particle Swarm Optimization-Based Method for Multi-Objective Design Optimizations[J]. IEEE Transactions on Magnetics, 2005, 41(5): 1756-1759.

[18]吴小刚，刘宗歧，田立亭，等. 基于改进多目标粒子群算法的配电网储能选址定容[J]. 电网技术, 2014, 38(12): 3405-3411.

(WU Xiaogang，LIU Zongqi，TIAN Liting，et al. Energy Storage Device Locating and Sizing for Distribution Network Based on Improved Multi-Objective Particle Swarm Optimizer[J]. Power System Technology, 2014, 38(12): 3405-3411. in Chinese)