液体火箭贮箱增压过程数值模拟研究

牛振祺，陈海鹏，褚洪杰，沈涌滨，汤 波

（1. 北京宇航系统工程研究所，北京，100076；2. 中国航天科技集团公司，北京，100048）

液体火箭贮箱增压过程数值模拟研究

牛振祺1，陈海鹏1，褚洪杰2，沈涌滨1，汤 波1

（1. 北京宇航系统工程研究所，北京，100076；2. 中国航天科技集团公司，北京，100048）

基于流体体积函数方法建立了N2O4贮箱的二维轴对称非稳态模型，对贮箱增压过程进行了数值模拟。通过模拟结果与火箭遥测数据的对比分析证明了模型建立的合理性。模拟结果显示，贮箱内外壁面温度接近，气枕顶部温度较高。将增压消能器等效处理为I、II两种结构。对于结构I，在飞行末期整个气枕存在明显的轴向温度分层，而结构II与I相比，贮箱顶部壁面附近的温度明显低于结构I的温度，且增压气体对液面没有明显冲击作用，在设计增压消能器时宜选结构II。

贮箱增压；温度场；数值模拟

0 引 言

液体运载火箭在火箭升空过程中需要一套增压输送系统来保证在泵入口要求的压力下将推进剂输入发动机。贮箱作为推进剂的存储装置，设计中对气枕压力与温度均有要求[1]。中国现役火箭中，常规推进剂氧箱经蒸发器加热后的高温、高压气体自贮箱顶部进入气枕，液体推进剂自贮箱底部排出。对于N2O4贮箱的增压排液过程，高温N2O4气体进入贮箱的自生增压方式是贮箱增压气体输送的一种重要形式，在这一过程中，由于气枕温升以及气体流动，增压气体与气枕原有气体、贮箱壁、液面等发生热交换，造成气枕及贮箱壁的温度分布发生变化，而温度分布又会对贮箱材料性能、气枕压力及保险阀的正常工作产生影响。因此，分析贮箱增压排液过程中气枕与壁面的温度分布对于贮箱的设计具有重要意义。

研究人员主要采用零维整体模型与一维分层模型分析增压过程中气枕温度、与气枕接触壁面温度、气枕压力等随时间的变化规律。零维整体模型假设气枕温度、气枕压力、与气枕接触壁面温度不存在空间分布，仅随时间改变，而一维分层模型不但考虑了各参量随时间的变化关系，也考虑了其沿轴向的分布规律。针对贮箱增压排液过程，研究人员所建立的零维及一维数学模型在预测气枕压力、气枕温度分布等方面具有一定的适用性，但仍存在不能展示箱内物理量的径向及局部分布等缺点[2～5]。近年来，随着计算流体力学技术（Computational Fluid Dynamics，CFD）的快速发展，将CFD方法应用于贮箱增压排液过程的数值模拟成为可能，它不仅能得到气枕温度、压力等参量的空间分布，还能获得各参量随时间的变化关系，弥补了零维模型和一维模型的不足。本文旨在应用CFD方法对贮箱增压过程进行数值模拟。

本文以火箭二级N2O4贮箱为研究对象，采用二维轴对称非稳态模型，应用VOF方法捕捉气液界面，忽略气液相之间的质量交换，着重分析壁面和气枕空间在增压气体输送过程中温度的变化，为液体燃料贮箱结构的优化设计提供初步理论依据。

1 贮箱壁面温度影响因素

贮箱增压过程实际上是箱内能量的一个分配问题，其基本过程如图1所示。

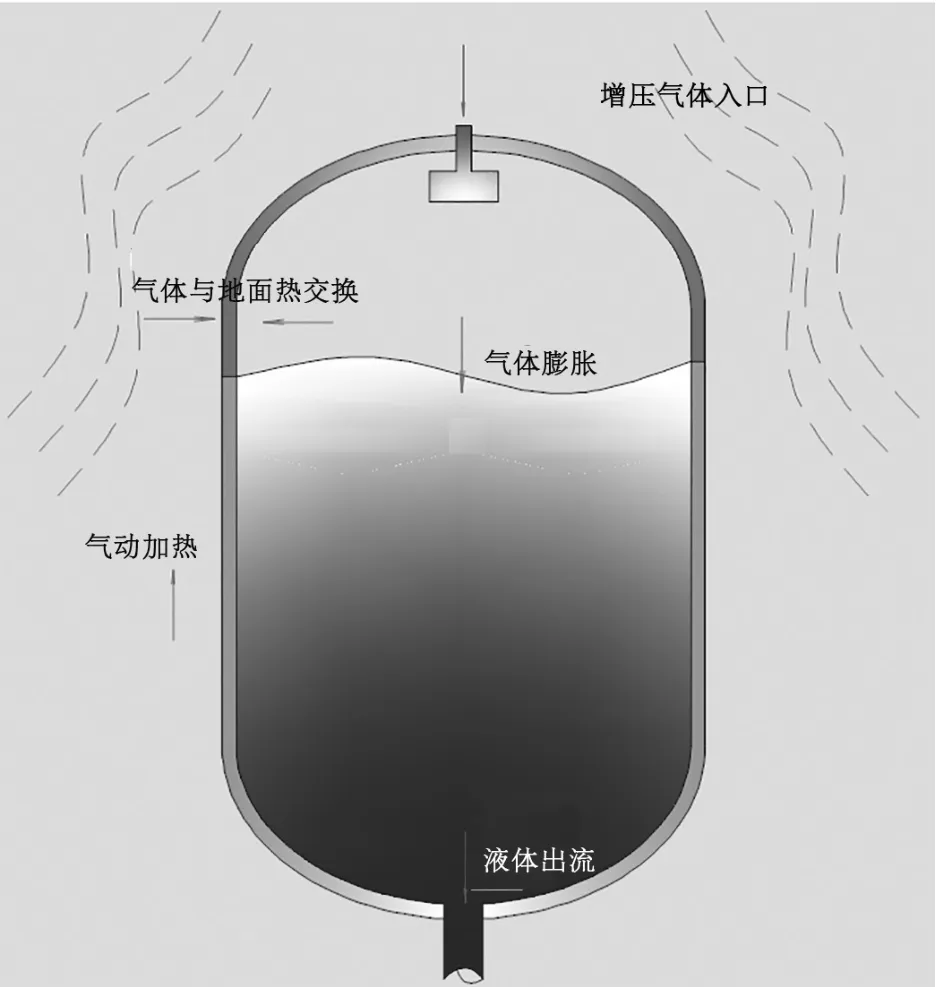
图1 贮箱增压过程原理示意

在一定输入能量流率的情况下，能量的主要分配项包括：a）增压气体和箱壁换热；b）气动加热输入热量；c）气体和液体换热；d）克服体积功；e）气体内能增加。壁面温度的变化是此过程中的一个重要环节。

从整个增压过程来看，对于壁面温度的影响因素主要包括：

a）贮箱外壁散热和气动加热；

b）进入贮箱增压气体介质种类、温度、流量；

c）贮箱增压压力；

d）推进剂种类、物性、表面行为特性及其温度；

e）贮箱结构型式、材料、壁厚；

f）箱内消能器布局型式；

g）工作时间。

对于二级N2O4贮箱的自生增压过程，根据以上对于壁面影响因素的分析及贮箱的工作条件，可作如下假设：

a）增压气体及推进剂的流量、温度为定值；

b）贮箱外界环境为真空，只存在辐射散热；

c）贮箱壁面厚度恒定；

d）由于N2O4气体在高温下基本上分解为NO2，增压气体成分假设只有NO2；

e）采用二维轴对称模型；

f）根据测量数据，二级氧箱安溢阀门打开时机较少，因此此计算中，不考虑安溢阀门打开因素。

2 物理模型

二级氧化剂贮箱由圆柱形的箱筒段和上下椭球形前后底组成，气枕位于贮箱前底，增压气体由增压消能器进入气枕，推进剂自出流口排出。增压管是一段弯曲的直径为50 mm的管道，在管路尾端的下表面开有34个直径为10 mm的出气孔，增压气体由出气孔排出。为了简化结构，便于建模，氧箱壁面厚度设为4 mm，二级氧箱的简化物理模型如图2所示。由于增压管是弯曲结构，且安装位置偏离贮箱对称轴，所以增压消能器只能应用三维模型计算，但三维模型计算量巨大，应用二维轴对称模型是一种有效手段。

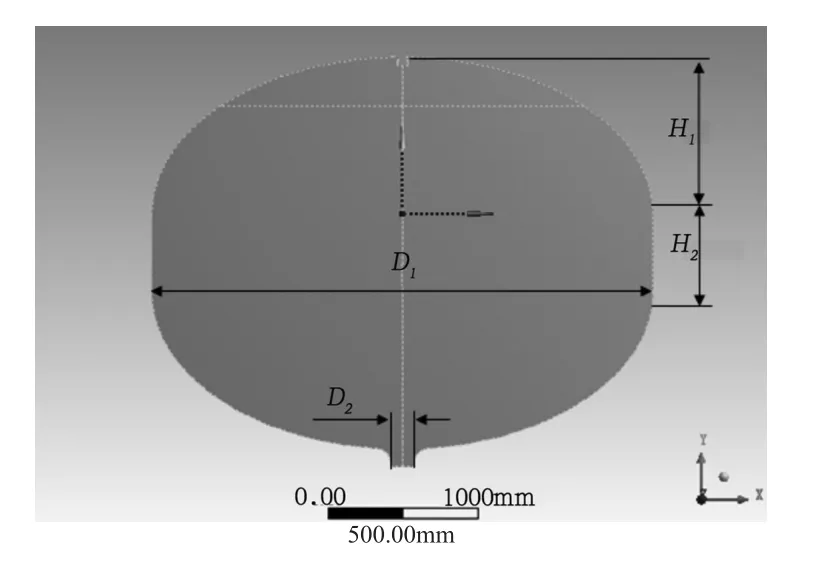
图2 简化贮箱结构物理模型

为比较不同增压消能器结构型式对流场和温度场的影响，特设置了两种结构型式。增压消能器结构根据出气孔面积进行二维等效处理，增压消能器的等效结构Ⅰ、Ⅱ示意如图3所示。等效结构Ⅰ的增压气体水平进入贮箱顶部，等效结构Ⅱ的增压气体沿半球形区域进入贮箱顶部。增压气体出流口单个小孔长度为3 mm（出流口作近似轴对称处理），结构Ⅰ有4个环形出口，结构Ⅱ有5个环形出口。

图3 增压消能器等效结构示意

在增压排液的初始时刻，贮箱内装有一定量的液态N2O4，温度为15 ℃，贮箱顶部为气枕区，NO2为增压介质，在一定的初始气枕温度和初始气枕容积下进行增压计算。由于二级氧箱外界环境为真空，贮箱外壁与环境的热交换方式只有辐射，贮箱外壁设置为辐射边界条件。

3 数学模型

针对二级贮箱物理模型，本文基于Ansys Fluent 13.0建立了二维轴对称非稳态模型，着重分析贮箱增压过程中气枕区各参数的变化规律。对于贮箱内的增压过程，气液相界面之间没有相互穿插和渗透，比较适合采用流体体积函数（Volume of Fluid，VOF）多相流模型捕捉两相之间的界面。

VOF方法由Hirt[6]提出，用于追踪两种或多种互不渗透流体相的相界面。在VOF方法中，对引入模型里的每一流体相，引入一相体积分数的变量。在每个控制容积内所有相的体积分数之和为1。VOF求解整个计算域内单一的动量守恒方程，如式（1）所示，计算得到的速度场由各流体相所共享。

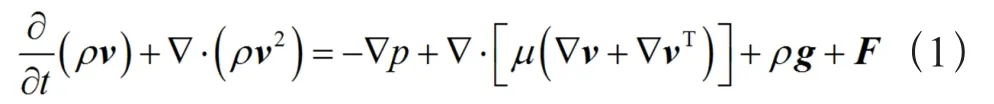
式中 v为速度向量；g为重力加速度向量；F为源项;ρ为密度；μ为粘度；动量方程取决于各相的平均物性ρ和μ，而平均物性由所有相的体积分数计算，对于气液两相流动，由下式表示：

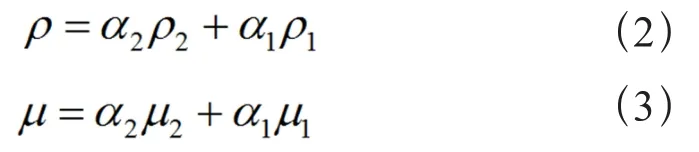
式中 α1，α2分别为气相和液相的体积分数。

在VOF方法中，跟踪不同相之间的界面是由求解单相或多相的体积分率的连续性方程得到的。在本文中，液相（液相为分散相）体积分率的连续性方程为

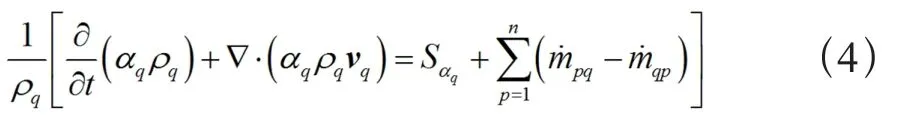
式中 αq为第q相流体的体积分率，0＜αq＜1表示计算单元中包含第q相流体与其它相流体的界面，αq=0表示在计算单元中没有第q相流体，αq=1表示计算单元中充满第q相流体，在本文的气液两相模拟中，第q相流体指的是液相，而主体相是气相，气相体积分数通过α1+α2=1来计算；为相q到相p的传质量；为相p到相q的传质量; sαq为源项，默认为0，也可将其定义为常数或自定义源项。本文的模拟中不考虑两相之间的传质。

对于具有低雷诺数的层流流动，N-S方程可以进行数值求解，且对物理模型没有任何要求。而对于高雷诺数的流动，则需要考虑湍流的影响，需引入湍流模型来封闭方程。为了考虑湍流的作用，本文采用RNG k-ε模型封闭方程。VOF模型中，与湍流有关的标量（如k、ε）输运方程在整个流场内也是由各流体相共用的。动量方程中的源项包括表面张力动量源项和气液相间作用力动量源项，本文只考虑表面张力作用。

VOF方法所用的表面张力模型是CSF（Continuum Surface Force）模型，由Brackbill等提出，本文只考虑表面张力为常数的情况，且只考虑界面法向的作用力。界面两侧的压力差为（p2-p1）：

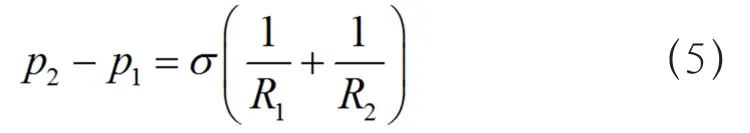
式中 σ为表面张力系数；R1和R2分别为相界面的双向曲率半径。

对于气液两相流动，由于表面张力而增加的动量源项表示为

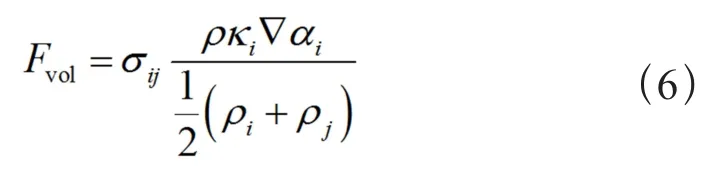
式中 ρ由式（2）计算得到；κ为相界面的曲率。本文在Fluent中设定NO2和液态N2O4之间的表面张力系数为0.025 61 N/m。

在Fluent的VOF模型中，壁面粘附模型可以和表面张力模型结合使用。对液相与壁面间粘附力的处理不是以边界条件的形式给出，而是将其计入表面张力动量源项。通常，流体与壁面形成的接触角的变化反映了固壁附近液相表面法向量的变化。固、液表面处相界面法向量可表示为

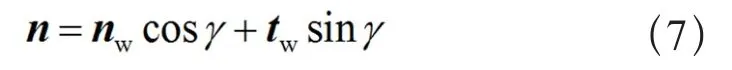
式中 nw和tw分别为壁面法向和切向的单位矢量；为固体表面的固液接触角。此接触角与离开壁面的单元远处的相界面法向共同确定了相界面的局部曲率，该曲率被用于调整表面张力计算中的体积力源项。本文设定固液接触角为90°。

采用氦增压的液氢贮箱增压过程研究表明，增压气体带入贮箱的能量当中，约有50%～60%通过气体与壁面换热传递给贮箱壁，同时有20%～25%的能量留在气枕区，其他热量则通过气液相间热质转移作用传递给液相[7]。因此气体与固壁换热、气液相间热质转移作用直接影响到数值模拟的正确与否。在本文的计算中，自生增压气体的主要能量通过与壁面换热传递给贮箱壁面，忽略气液相之间的传质，着重考虑流体与固壁的耦合换热作用，因此将包括金属壁在内的整个区域划分网格，壁面厚度划分为4层网格，在流体相近壁面区域和增压气体入口区域进行网格加密处理，总网格数为84 301。近壁区的流固耦合换热采用Fluent中的增强壁面函数方法求解，设定壁面厚度为4 mm，软件将自动激活相应的导热模型。贮箱内壁面设置为无滑移静止边界条件，外壁面设置为辐射边界条件。贮箱二维轴对称模型的网格划分和边界条件设置如图4所示。图4中液态N2O4出口设为质量流量出口边界条件。

图4 二维轴对称模型的网格划分和边界条件设置

计算中假定重力场恒定（9.8 m/s2），对称轴为X轴，重力方向为X轴正方向，非稳态计算的时间步长取为0.01 s，计算总时间为125 s。NO2气体密度采用理想气体模型计算，NO2气体的其他物性参数采用Fluent自带数据库数据；液态N2O4的密度计算采用Boussinesq模型，密度参考值设为1455.75 kg/m3，比热设为1515.6 J/(kg·K)，粘度（20 ℃时）为0.418 9×10-3Pa·s，热导率（20 ℃时）为0.153 516 w/(m·K)，液态N2O4的热膨胀系数设定为0.001 06 K-1。计算初场静止。对于参量的离散格式，压力项采用PRESTO!格式，体积分数项采用Geo-Reconsturc格式，其他参量均采用二阶迎风格式。压力速度耦合项选用基于压力隐式算子分裂（Pressure Implicit with Splitting of Operators，PISO）算法修正压力值。

4 计算结果与遥测数据的对比

根据上面的物理和数学模型，结合相应的边界条件，基于Ansys Fluent13.0求解得到计算结果。为了验证计算结果的有效性，本文将模拟结果与火箭遥测数据进行了对比分析。

首先对二级氧箱前底壁温的结果进行了对比。图5为二级氧箱前底壁面温度点标识。氧箱前底测温点位于图5中的1007点，其余温度点依次向后推移。图6为不同的温度标识点的模拟结果和遥测结果。由图6可以看出，随着飞行时间的推移，温度均呈增大的趋势。离前底增压消能器越远，温度上升越慢。遥测结果与916点的模拟结果吻合良好，但与测温点1007的模拟结果相差较大，1007点温度高于遥测结果。

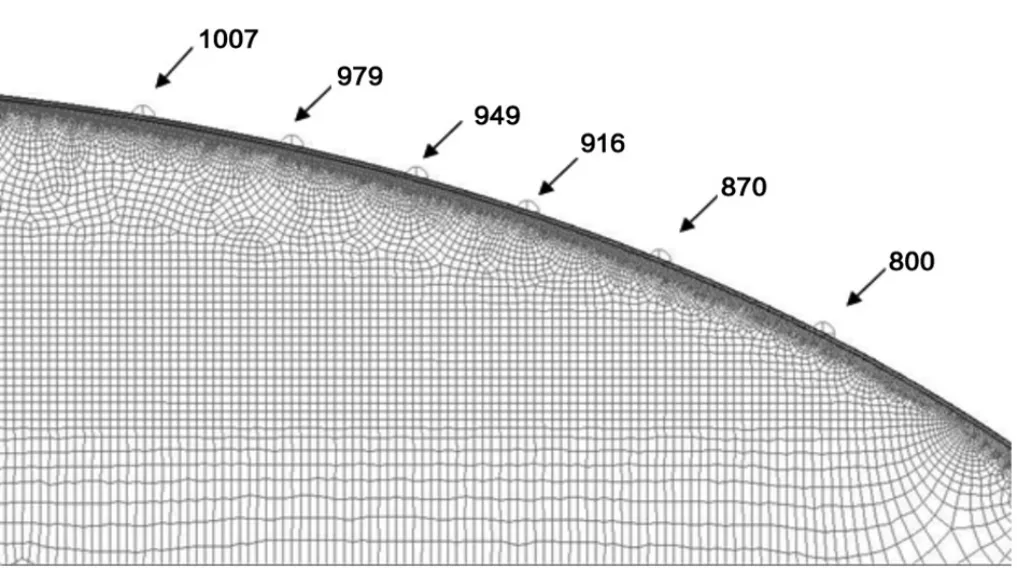
图5 二级氧箱前底壁面温度点标识

图6 二级氧箱前底壁温结果对比

图7为二级氧箱气枕内温度传感器测点的计算结果与测量结果。由图7可以看出，计算结果高于遥测结果。这是由于在建立物理模型时对增压消能器进行等效处理，贮箱内部流场与真实结果存在偏差，由此得到的计算结果也存在偏差。增压消能器的气体出口的流动方向为沿水平和轴向的半球型区域，而本文所用的二维轴对称模型将其等效为气流沿水平方向吹扫，高温气流势必会对贮箱壁产生额外的加热作用，因此计算结果要高于遥测结果。这样的结果可以用于贮箱的结构设计，因为贮箱壁温的计算只需得到其最大理论值，以此用于贮箱结构的校核计算。此外，图7中的气体温度计算值出现上下振荡的现象，这是因为增压气体沿水平方向流出，气流速度较大，气流的湍流脉动强度也较大，导致温度出现振荡。

二级氧箱的气枕压力的计算结果和遥测结果如图8所示。

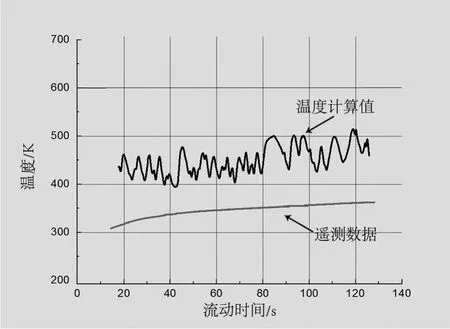
图7 二级氧箱气体温度结果对比

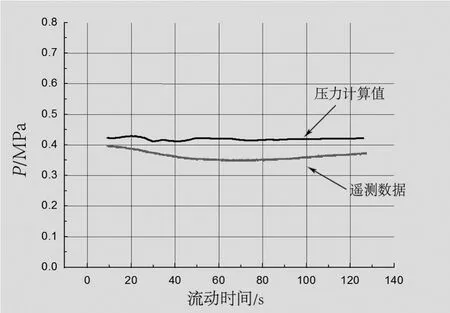
图8 二级氧箱气枕压力结果对比

从图8可以看出，计算值与遥测测量值基本吻合。造成结果偏差的主要原因是在对气体相进行物性计算时，假设只有N2O4的分解产物NO2，而实际增压气体是N2O4和NO2的混合物。因为1 mol的N2O4对应2 mol的NO2，因此数值模拟结果预测的贮箱压力比实际值偏大。

通过以上对贮箱壁面温度、气体温度和压力的结果对比，可以得出，本文建立的模型合理，可以用于贮箱壁面和气枕温度的分析。

5 壁面和气体温度分析

图5中的800点附近内外壁面的温度如图9所示。从图9可以看出，内外壁面温度非常接近，这是由于壁面材料为铝合金，热传导性能良好。此外，由于外壁面向真空进行辐射散热，因此，外壁温度稍低于内壁温度。

图9 内外壁面温度比较（800点）

图10为增压消能器为等效结构Ⅰ时22.75 s、58.75 s、94.75 s、124.75 s 4个时刻的气枕温度场等值线。火箭飞行过程中，高温气体自贮箱顶部进入气枕，造成气枕顶部温度较高，而底部由于液面的冷却作用温度较低，在飞行末期整个气枕存在明显的轴向温度分层。图10的模拟结果也验证了这一点，并且径向在靠近壁面处的温度高于气枕中心温度，气枕区域的上部较为明显。高温增压气体自增压消能器进入气枕，由于来流速度较大，高温气流直接冲刷贮箱壁面，同时由于浮力的作用，气流在流向壁面的过程中向上倾斜，造成增压口正对偏上位置的壁面直接面对气流冲刷，温度最高。在增压消能器气流出口附近的气枕顶端区域，气体扰动最大，径向存在明显的温度局部分布，这是贮箱零维或一维模型所不能得到的。增压气流碰到壁面后又开始沿壁面向下流动，并在流动过程中动量逐渐降低，造成靠近壁面的气枕温度高于中心温度。

图10 不同时刻气枕温度场等值线（等效结构Ⅰ）

增压消能器为等效结构Ⅱ时在17.19 s、53.19 s、89.19 s和125.19 s 4个时刻的气枕温度场等值线如图11所示。由图11可以看出，结构Ⅱ与Ⅰ相比，温度场差异很大，且贮箱顶部壁面附近的温度明显低于结构Ⅰ的温度，这对贮箱壁面有利，此外，增压气体对液面的冲击作用不明显，因此，在设计增压消能器时宜选结构Ⅱ。造成气枕内部温度场分布的主要原因是增压气体流场的分布，在增压初期，气体由增压消能器出流口呈半球放射状喷出，由于来流的惯性作用，靠近贮箱轴线的出流口的气体射流速度较大。之后放射状气流动量逐渐降低，当气流到达贮箱液面时，靠近贮箱轴线的液面被速度较高的中心气流冲出小的凹坑。然后气流被液面分成对称的两股气流，分别沿液面向壁面方向流动，同时由于液面、壁面的阻挡，以及气流的浮升力作用，对称的两股气流在抵达壁面后转而向上流动。

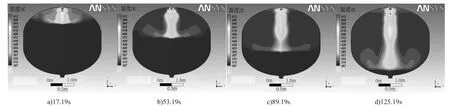
图11 不同时刻气枕温度场等值线图（等效结构Ⅱ）

图12为等效结构Ⅰ、Ⅱ增压过程末期壁面温度沿轴向的分布。对于等效结构Ⅰ，温度分布云图展示了贮箱壁面温度沿轴线向下逐渐递减的过程，随着增压过程的进行，气枕区域逐渐扩展，气枕内的气体量逐渐增大，气枕下部温度逐渐升高，与气枕接触的壁面区域也逐渐被加热，此外，贮箱壁面内部沿轴向的导热对壁面也有加热作用。而对于等效结构Ⅱ，没有明显的轴向温度分布，只有在紧靠增压消能器处的壁面温度较高，因此，图12的温度云图进一步证明在设计增压消能器时宜选结构Ⅱ。

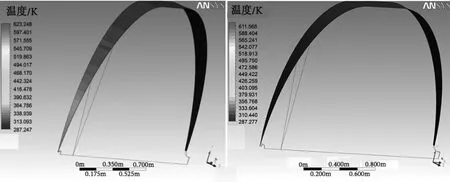
图12 增压过程末期壁温沿轴向分布

6 结束语

本文针对N2O4贮箱的自生增压过程，根据壁面影响因素的分析及贮箱的工作条件，对物理模型进行了简化处理，并基于VOF方法建立了二维轴对称非稳态模型，对贮箱增压过程进行了数值模拟。通过将壁温、气体温度、压力的模拟结果与火箭遥测数据的对比分析，可以证明本文建立的模型是合理的，可以用于贮箱壁面和气枕温度的分析。为比较不同增压消能器结构形式对流场和温度场的影响，本文将增压消能器等效处理为Ⅰ、Ⅱ两种结构。数值模拟结果得到了气体温度和贮箱壁面温度的变化规律，模型可以预测气枕区域轴向和径向的温度分布。结果显示，贮箱内外壁面温度非常接近，火箭飞行过程中，高温气体自贮箱顶部进入气枕，造成气枕顶部温度较高，而底部由于液面的冷却作用温度较低。对于等效结构Ⅰ，在飞行末期整个气枕存在明显的轴向温度分层，而等效结构Ⅱ与Ⅰ相比，由于气枕内部流场分布的变化，造成温度场差异较大，且贮箱顶部壁面附近的温度明显低于结构Ⅰ的温度，在设计增压消能器时宜选结构Ⅱ。

[1] 张超, 鲁雪生, 田丽亭. 火箭低温推进剂增压系统数学模型[J].低温与超导, 2005, 33(2): 35-38.

[2] Zilliac G, Karabeyoglu M A. Modeling of propellant tank pressurization [R]. AIAA 2005-3549, 2005.

[3] Roudebusb W H. An analysis of the problem of tank pressurization during outflow[R]. NASA TND-2585, 1965.

[4] 张勇, 李正宇, 李强, 等．低温液体储箱加压排液过程计算模型比较[J]. 低温工程, 2007(2): 25-27.

[5] Roudebusb W H. An analysis of the problem of tank pressurization during outflow[R]. NASA TND-2585, 1965.

[6] Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. J Comput Phys, 1981, 39(1): 201-225.

[7] Stochl R J, Maloy J E, Masters P A, et al. Gaseous-helium requirements for the discharge of liquid hydrogen from a 3.96-meter- (13-ft-) diameter spherical tank[R]. NASA TN D-7019, 1970.

Numerical Study on Tank Pressurization Process of Liquid Rocket

Niu Zhen-qi1, Chen Hai-peng1, Chu Hong-jie2, Shen Yong-bin1, Tang Bo1
(1. Beijing Institute of Astronautical Systems Engineering, Beijing, 100076; 2. China Aerospace Science And Technology Corporation, Beijing, 100048)

A two-dimensional axisymmetrical model based on volume of fluid (VOF) method is set up to solve the unsteady process of nitrogen tetroxide(N2O4)tank. The model is used to simulate the tank pressurization process. The validity of model is tested through the comparison with the experimental data of flight. The simulated results provided the distributions of ullage temperature and wall temperature of tank. The inner and outer wall temperature of tank is almost equal. The maximum temperature is located at the top of tank ullage. In this paper, the pressurized gas injector is equivalent to two structures of I or Ⅱ. For the structure of Ⅰ, thermal stratification of tank ullage is obvious during the flight, and the temperature at the top of tank ullage is higher than the result of structure of Ⅱ. The impact of pressurized gas to propellant liquid is negligible for the structure of Ⅱ. Therefore, the structure of Ⅱ is superior to the structure of I.

Tank pressurization; Temperature field; Numerical simulation

V41

A

1004-7182(2016)05-0016-07

10.7654/j.issn.1004-7182.20160504

2015-07-09；

2016-04-20

牛振祺（1985-），男，博士，高级工程师，研究方向为火箭流体系统