功能梯度压电材料的参数处理与自由振动特性分析

卿光辉，吴宏伟

（中国民航大学航空工程学院，天津　300300）



功能梯度压电材料的参数处理与自由振动特性分析

卿光辉，吴宏伟

（中国民航大学航空工程学院，天津300300）

摘要：随着压电材料的应用越来越广泛，对压电材料的性能分析也越来越受到重视。针对功能梯度材料固有频率的分析，采用ANSYS 12.0中的Solid98单元进行分析，在此基础上采用ANSYS中的APDL语言进行编程，为实现参数的变化，假定材料的所有性能参数是变化且按同一方向进行变化，变化的方向为板厚方向，从而实现了压电材料性能的梯度化变化，并对其固有频率做了计算与探讨。

关键词：功能梯度；压电；ANSYS；固有频率

功能梯度材料（functionallygradedmaterials，FGM），即材料本身的构成与布局连续变化，材料的宏观特性，诸如弹性模量、压电系数不会发生跳跃性的变化，而在空间上呈现梯度变化，此种材料性能可以减轻或者解决应力集中的问题。当结构的不同位置有着不同的参数要求时，可以提供相应的功能，改善结构的整体性能。而功能梯度压电材料（FGPM）的出现，则更进一步解决了压电材料物理性质与结构材料不匹配造成的应力集中现象，使得智能结构与传感器的机电耦合性能得到更大程度的发挥。

压电材料可以用于很多方面，压电驱动器和传感器就是典型的例子。合理运用压电驱动器和传感器，首先需要计算力与电场对压电板的具体影响。大量文献研究了如何对均匀压电板进行三维控制，也给出了相应的精确解。HUANG等[1]建议沿着厚度方向对位移和电势进行坐标展开，运用傅立叶级数来描述动态响应。但有时傅立叶级数并不能很方便地解出，因此在对未知傅立叶级数进行求解时，需要有特殊的边界条件和外部输入。GAO和SHEN等[2]对自由振动问题的精确解进行了研究，分析的模型为压电层合板，求解方法为幂级数展开法。但考虑到压电功能梯度板的材料性能会沿着板厚的方向进行变化，因此想要求解三维压电方程是相当困难的。LIU等[3]研究了波在FGPM板中的传播特性，采用的方法为混合数值法。CHEN 和DING[4]对弯曲问题做了一些探讨，其模型基于压电功能梯度板，而分析方法则是基于状态方程。同时CHEN和DING[5]还针对自由振动问题进行了分析，所用模型也为压电功能梯度板，形状为矩形。

考虑到一般的有限元软件只能分析参数均匀的压电结构，而本文需要对材料参数呈梯度变化的压电结构进行分析，故采用ANSYS 12.0中的APDL语言进行编程，实现材料的梯度变化，从而实现对功能梯度材料的振动频率进行模拟。

1　基本理论与公式

对于一块压电梯度板，沿着z轴进行了极化，在弹性体内沿x，y，z方向的运动平衡方程为

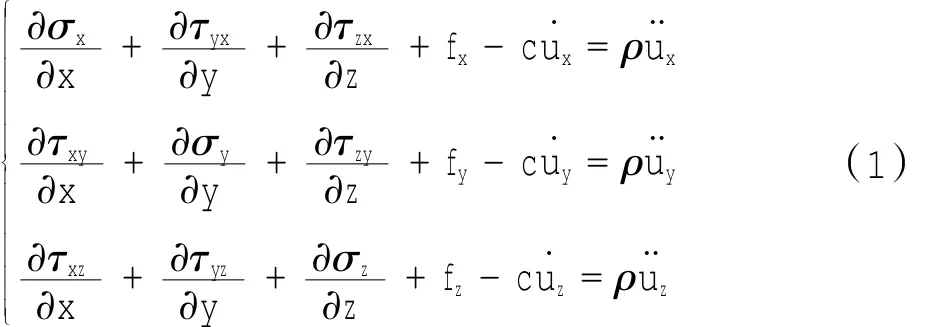
其中：fx，fy，fz分别为沿着x，y，z方向的单位体积的体积力；c为材料阻尼系数，u为位移。

压电材料的电学平衡方程为

其中：Dx，Dy，Dz分别是x，y，z方向的电位移

线性压电梯度材料的本构方程为

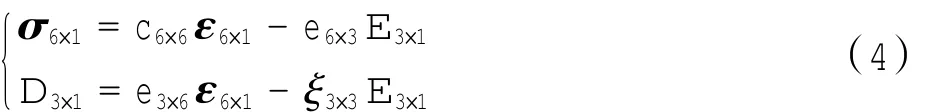
其中：σij为应力张量，Di为电位移向量，εkl为应变张量，Ek为电场强度向量，cijkl为弹性常数，eikl为压电应力系数，ξik为介电常数。

在这里，材料力学和电学常数不是固定的，它们都沿着板厚的方向进行变化。变化规律则可用同一函数

矩阵形式为来表示，其中K可以代表弹性刚度系数、压电常数或应变介电系数，K0是相应的材料常数在处的值[6]。

根据有限元的基本理论，材料的有限元单元耦合方程为

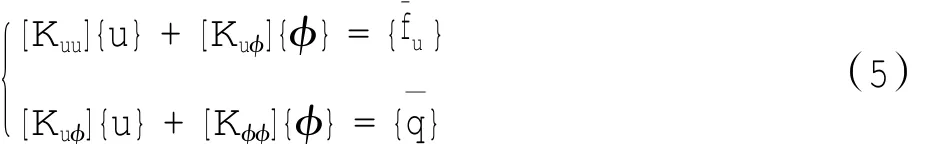
其中：[Kuu]是结构刚度矩阵，[Kφφ]是介电常数矩阵，[Kuφ]是压电耦合矩阵，是作用的边界条件。

2　参数分析与APDL语言程序

运用ANSYS进行有限元分析主要包括如下步骤：建立模型、定义参数、划分网格、问题求解。而APDL语言的作用在于可将输入灵活化，使用者可根据自身需要输入自己设定的函数或者分析标准，可以说这是一种比较智能的技术措施。这种分析手段充分给予使用者自主能力，可以让使用者自由修改设计或分析属性。在传统有限元分析的基础上，该语言扩充了额外的分析能力，对于更高级的灵敏度研究、参数化建模也有着很好的分析能力[7]。

不同于一般的建模方式，功能梯度材料的性能是沿厚度方向变化的，因此需要对其进行分层建模，但是这种建模也难以脱离基本的层合板理论，可以视为基本层合板理论的一种延伸。建模时可根据计算的精度和计算机的运算能力确定所需要的层数。在进行模型网格划分时，需要给每一层模型赋予材料属性[8]。由此可知，当需要按照要求变化数据时，就需要采用APDL语言来进行编程计算。

利用ANSYS分析时，采用Solid98单元，这是一种10节点的Tetrahedral，该单元在分析体模型或划分不规则形状时特别有优势[9-10]，如图1所示。

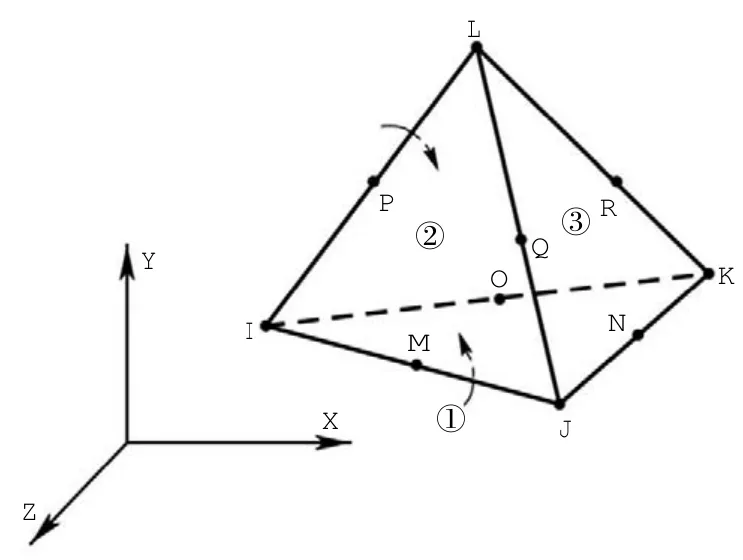
图1　Solid 98单元Fig.1 Solid 98 elem ent

Solid98单元共有10个节点，分别为图中的I、J、K、L、M、N、0、P、Q、R[11]。在单元中，可以根据需要控制其自由度，而自由度是由KEYOPT（1）这一选项的值来确定的[12-14]。在对压电材料进行分析时，通常把KEYOPT（1）的值设置为3，相应的自由度分别为UX、UY、UZ和VOLT。

采用APDL语言编写的计算程序为

3　算例分析

考虑一个四边简支的功能梯度压电板，板的长度和宽度分别为a= 1 m和b = 1 m，板厚为h并且满足关系式：2h/a = 0.1，0.2，0.3，假设压电材料PZT-4材料为功能梯度板的底面材料，其弹性系数、密度的材料常数如表1所示[10]。功能梯度材料的性能参数变化规律为，材料属性梯度变化系数k = 0，0.1，1.0，2.0，3.0。以下计算功能梯度压电板在四边简支情况下的自振频率。

表2给出了不同梯度变化情况下功能梯度压电材料板的固有频率，并与文献[15]的有限元计算结果作了比较。

由数据分析可知，对与梯度分布情况相同的压电板，随着板厚的增加，板厚的固有频率也随之增加。随着压电板属性梯度幅度的增大，压电板固有频率则随之减小。很明显，材料属性梯度变化系数k的改变，压电材料的性能参数在厚度方向上也随之发生改变。从数据可看出：对于k = 2.0，3.0，当系数变化时，频率的下降幅度很小，但随着板厚的增加，频率的下降幅度越来越大。由误差数据可以看出，随着板厚的增加，误差总体上呈现出下降趋势，这是由于随着板厚的增加，有限元划分的网格越来越规则，因而计算精度也随之提高。

应当指出，相比于六面体单元，文中采用的Solid 98单元适合分析形状不规则的物体与单元，因而适用性更广，在实际中应用更多。当然，对于实际中的有些问题，将六面体单元与四面体单元结合起来分析，可能会得到更好的效果，这也是需要进一步研究的内容。

表1　PZT-4的材料常数Tab.1 M aterial constant of PZT-4

表2　功能梯度板的固有频率Tab.2 Natural frequency of functionally graded plate

4　结语

本文利用ANSYS的压电分析模块对功能梯度压电层合板进行了分析，利用APDL参数程序化设计程序实现了性能参数的梯度化，对其振动频率进行了计算，同时，文中采用了Solid 98单元，该单元对于构造体模型和不规则形状的网格划分有着独特的优势。通过计算结果的分析可知：固有频率与文献中的精确解基本一致，因此利用APDL语言对材料功能梯度化处理方法是可行的。

参考文献：

[1] HUANG JH，YU H I.Dynamic electromechnical response of piezoelectric platesassensorsoractuators[J].Materials Letters，2000，46（2-3）：70-80.

[2] GAO JX，SHEN Y P，W ANG J.Three dimensional analysis for freevibration of rectangular composite laminateswith piezoelectric layers[J]. Journalof Sound and Vibration，1998，213（2）：383-390.

[3]曹宗杰，闻邦椿.含压电材料智能结构动态特性的研究[J].计算力学学报，2001，18（3）：267-272.

[4] CHEN W Q，DING H J.Bending of functionally graded piezoelectric rectangular plates[J].ActaMechanica Solida Sinica，2000，13（4）：312-319.

[5] CHEN W Q，DING H J.On free vibration of a functionally graded piezoelectric rectangular Plate[J].Acta Mechanics，2002，153（3-4）：207-216.

[6]刘玮，丁丽霞.基于不同梯度模式压电功能梯度板的挠度和应力场分析[J].吉林大学学报，2005，43（5）：36-37.

[7] LIU G R，TANIJ.Surface wave in functionally gradient piezoelectric plates[J].JournalofVibration&Acoustias，1994，116（4）：440-448.

[8]高坚新，沈亚鹏，王子昆.有限长压电层合简支板自由振动的三维精确解[J].力学学报，1998，30（2）：168-177.

[9]仲政，尚尔涛.功能梯度热释电材料矩形板的三维精确分析[J].力学学报，2003，35（5）：542-552.

[10]陈伟球，叶贵如，蔡金标，等.横观各向同性功能梯度材料矩形板的自由振动[J].振动工程学报，2001，14（3）：263-267.

[11]黄小林，沈惠申.带压电层功能梯度复合材料混合层合板的自由振动和动力响应[J].强度与环境，2004，31（2）：13-19.

[12]尹林，王晓明，沈亚鹏.用压电元件实现复合材料层合板振动控制的数值分析[J].振动工程学报，1996，9（2）：107-115.

[13]黄小林，沈惠申.热环境下贴压电层的功能梯度材料板的自由振动和动力响应[J].应用力学学报，2005，22（3）：456-459.

[14]王国强.实用工程数值模拟技术及其在ANSYS上的实践[M].西安：西北工业大学出版社，2000.

[15]TSAIY H，W U C P.Dynamic responsesof functionallygraded magnetoelectro-elasticshellswithopen-circuitsurfaceconditions[J].International Journalof Engineering Science，2008，46（9）：843-857.

（责任编辑：刘智勇）

Param eter processing and free vibration characteristic analysis of functionally graded piezoelectricm aterials

QING Guanghui，W U Hongwei
（College of Aeronautical Engineering，CAUC，Tianjin 300300，China）

Abstract：W ith the growing application of piezoelectricmaterials，the characteristic analysis of piezoelectricmaterials is takenmore andmore seriously.For the natural frequency analysis of functionally gradedmaterials，the Solid 98 element in the ANSYS 12.0 and the parameter designing of APDL language are adopted，supposing that the characteristic parametersof thematerial change alongwith the thicknessof the plate.The gradientchange about characteristic parameters of piezoelectricmaterial is realized，and natural frequency of the functionally graded piezoelectric laminate isanalyzed.

Key words：functionally gradient；piezoelectricity；ANSYS；natural frequency

作者简介：卿光辉（1968—），男，湖南湘潭人，教授，博士，研究方向为复合材料力学.

收稿日期：2014-12-29；修回日期：2015-03-01基金项目：国家自然科学基金项目（60979001）

中图分类号：O177.91；O241.7

文献标志码：A

文章编号：1674-5590（2016）01-0036-04