基于静电场模型的自由飞行空域冲突探测方法

张　喆，黄晓晓，吴仁彪

（中国民航大学天津市智能信号与图像处理重点实验室，天津　300300）



基于静电场模型的自由飞行空域冲突探测方法

张喆，黄晓晓，吴仁彪

（中国民航大学天津市智能信号与图像处理重点实验室，天津300300）

摘要：针对自由飞行空域中飞行活动自由、飞行条件复杂、易发生飞行冲突等特点，提出了一种基于静电场模型的自由飞行空域冲突探测方法。本方法使用点电荷类比自由飞行空域中的飞行活动，则点电荷之间的库仑力可表征空域中飞行活动之间的相互影响程度，系统的电势能则可体现空域中飞行活动之间冲突的严重程度。本方法同时具备多飞行活动之间冲突群的探测能力，也为自由飞行空域的飞行冲突探测和冲突解脱方法提供一种新的思路。

关键词：自由飞行；冲突探测；静电场模型

在自由飞行体系中，飞行员可以更加自由灵活地选择适合自己的航路和速度，以自定义的最快捷、最经济的路线飞行[1]。消除以往飞行器必须集中到狭窄航线上飞行的弊端，自由飞行可以有效提高空域的利用率。然而，处于自由飞行状态的飞行器将会出现在任何时间和任何地点，每一架飞行器都不可能单独地占用整个空域，其周围可能有许多飞行器同时飞行，飞行器所遇到的冲突可能不仅仅只涉及一架飞行器，多架飞行器之间可能会发生多个冲突。因此，研究一定空域内飞行器与飞行器之间以及多架飞行器之间的冲突探测问题具有重要的实际意义。

然而，现有的冲突探测方法，无论是概率型冲突探测还是确定型冲突探测，关注的都是2架飞行器之间的冲突特性，如冲突时间、当前距离等，无法同时研究多架飞行器之间的冲突。另一方面，当前大多数冲突探测方法仅仅针对飞行器沿固定航路飞行的情况，而在自由飞行中，飞行员的意图成为影响飞行航线的最主要因素，这使得传统的冲突探测方法难以有效发挥作用[2-6]。

针对上述问题，本文基于静电场理论[7]，不将飞行器沿预定航路飞行作为条件，提出一种适用于自由飞行条件下的冲突探测方法。通过将飞行器类比为理想电荷，空域能量与空域中飞行器数量以及飞行器之间距离的大小相关，利用空域能量的变化作为标准来衡量飞行器距离的变化，以此进行2架飞行器之间的冲突探测或者多机冲突群的探测。

1　模型原理

在空中交通管制中，为保证飞行安全，飞行器之间必须保持一定的间隔。违反间隔标准，将会引起冲突。随着两飞行器距离的不断接近，冲突的等级也将不断严重[8-9]。

根据静电场理论，真空中的点电荷与周围电荷之间存在相互作用的库仑力，库仑力的大小与它们之间距离的平方成反比。也就是说，随着两个电荷距离的减小，它们之间的电场强度不断增加，电荷之间累积的能量也越大。类比于此，若将某时刻空域中飞行的飞行器看做是在特定位置的理想电荷，则该飞行器对整个空域将产生电场能量，且单架飞行器对整个空域产生的能量不随飞行器位置的变化而变化。在飞行器距离不断接近的过程中，空域累积的能量不断增大，同时整个空域的平均能量也越大。

将空域中某位置的飞行器看做理想带电电荷，其对整个空域产生的场强满足下面的关系

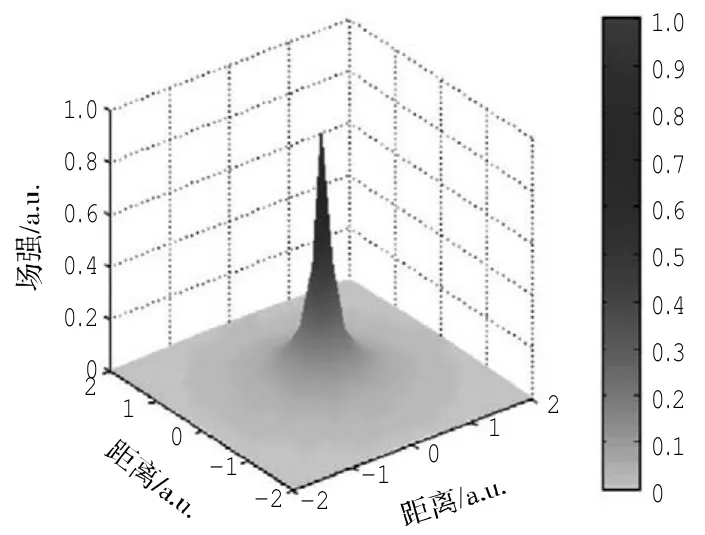
图1　单架飞行器对其周围区域产生的场强分布Fig.1 Electrostatic field intensity around aircraft

2　模型建立

空域以相等间隔划分为正方形网格，将飞行器类比为点电荷，则单架飞行器Ai在空域各网格顶点产生的电场强度为

根据场强的叠加定理，N架飞行器A1，A2，…，AN对空域各个网格顶点产生的电场强度满足

图2所示为2架飞行器对空域各个网格顶点产生的场强分布图。其中，空域以5 km为间隔划分为24×24个正方形网格，共25×25个网格顶点。飞行器位置分别为（72.5 km，62.5 km）、（52.5 km，62.5 km）。

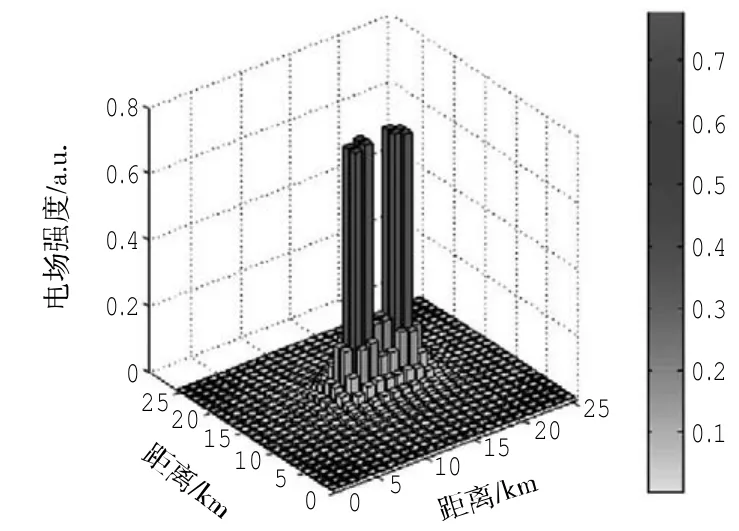
图2　2架飞行器对空域各个网格点产生的场强分布Fig.2 Electrostatic field intensity on grids’vertices

为讨论方便，现考虑飞行器均位于空域中的同一巡航高度，即二维情况。模型本身对三维情景同样适用。依据N架飞行器所产生的电场分布，整个空域中所储存的电场能量与平均能量分别由式（5）～式（7）所定义，即

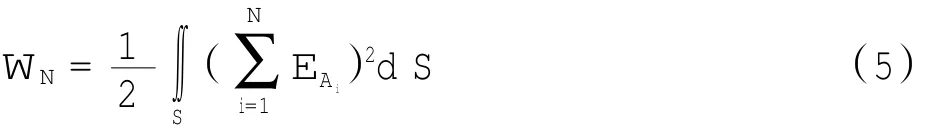
其中：EAi为单架飞行器Ai在空域各网格顶点产生的电场强度；N为飞行器架数。考虑空域被划分为若干边长为d的正方形网格，若X轴方向共k个网格，Y轴方向共l个网格，式（5）可转化为离散状态下的表达式，即

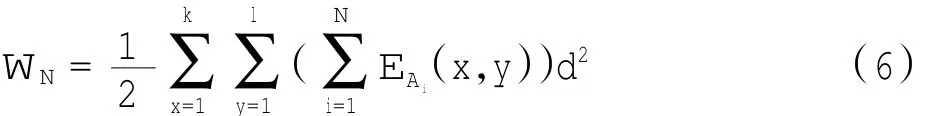
N架飞行器对空域产生的平均能量为

N架飞行器在排列最紧密的情况下保持最小安全间隔且互相无冲突的飞行，将整个空域看做一个整体，此时空域处于安全的临界状态，空域中由N架飞行器引起的平均能量将达到安全状态下的最大值。当某时刻空域能量超过该最大值，说明N架飞行器分布过于密集，必然存在着冲突群现象。能量越大，说明冲突飞行器数量越多或者冲突等级更严重，空域危险性更高。反之，能量越小，飞行器分布越分散，相互之间距离越远，空域安全性更好。

3　数值模拟

3.1单一冲突情况

研究空域为120 km×120 km的正方形区域，考虑二维情况，即2架飞行器A和B位于同一巡航高度，飞行器水平方向最小安全间隔为10 km，以500 m为间隔将空域划分为若干正方形网格。式（3）中平滑参数a= 1。飞行器A初始位置为（25 km，25 km），速度vA=（0.25，0.25）km/s；飞行器B初始位置为（95 km，25 km），速度vB=（-0.25，0.25）km/s。A、B两飞行器航迹如图3所示。

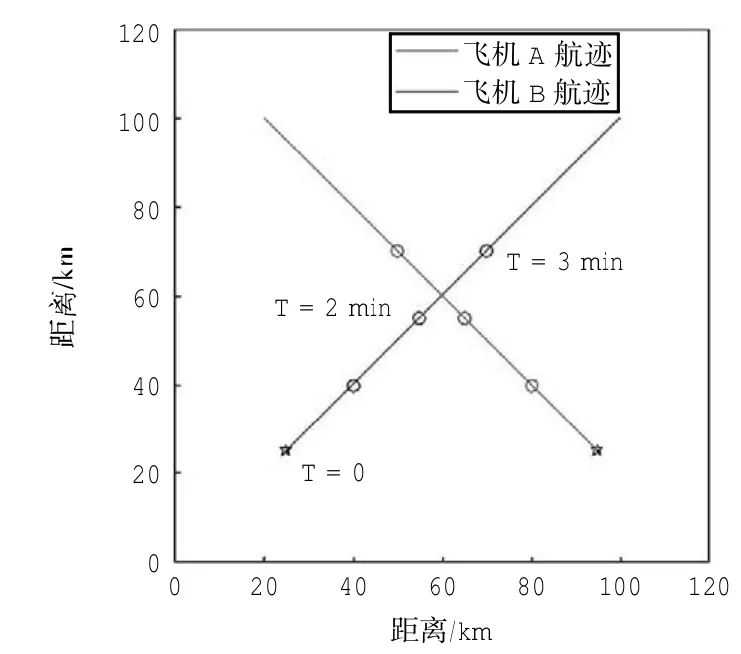
图3　两飞行器飞行态势图Fig.3 Flight scenario of two aircrafts

图3中，初始时刻两飞行器相距70 km，分别以初始速度匀速运动。1min后，两飞行器相距40 km，2min后，两飞行器间距达到最小安全间隔，存在短期冲突。此时空域平均能量为3.4 a.u.。文中场强与能量的单位均为任意单位（a.u.）。为了清楚描述飞行器运动过程中整个空域能量的变化，假设飞行器在冲突情况下继续沿原来航向飞行，且相遇后背离飞行。从T=0时刻开始，研究5 min内整个空域平均能量的变化，如图4所示。从图中可以看出，初始时刻由于A、B两架飞行器相距较远，整个空域的平均能量低。随着飞行器距离的不断减小，空域平均能量随之增大，能量最大值点对应两飞行器间距为0的点。由曲线的对称性可知，空域平均能量与飞行器间隔成正比，而与飞行器在空域中的位置无关，能量的变化能很好地反映出飞行器间隔的变化。因此可选取两飞行器相距最小安全间隔时刻空域的平均能量作为阈值，即等于3.4 a.u.，以此来判断2架飞行器是否存在短期冲突。当某时刻空域平均能量大于该阈值时，说明此时两飞行器距离小于最小安全间隔，存在飞行冲突。

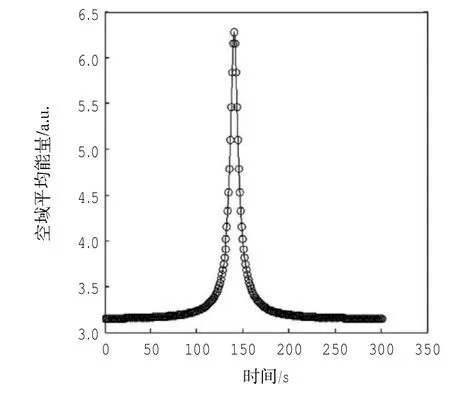
图4　5 m in内空域平均能量的变化Fig.4 Average airspace energy change 5 m inutes

3.2多冲突对情况

对于N（N≥3）架飞行器的冲突探测，考虑N架飞行器安全飞行状态下最密集的分布作为临界状态，即两两飞行器之间均保持最小安全间隔无冲突条件下，占用最小空域面积的飞行态势。由正多边形的镶嵌规律可知，在正多边形中，只有正三角形、正方形与正六边形3种图形能够用来铺满1个平面而中间没有空隙，6个正三角形镶嵌为1个正六边形，4个正方形镶嵌为1个正方形。因为1个正方形仍然可以分解为2个等腰直角三角形，因此以三角形为基本单位研究飞行器的排布。设飞行器间最小间隔为D，图5中左边一列是以D为边长的等边三角形组合排列法，右边列是以D为边长的等腰直角三角形排列法。

图5　多架飞行器安全状态下最紧密的排布示意图Fig.5 M ost close arrangem ent of aircrafts in safety state

对于图5中的每个等边三角形与等腰直角三角形来说，等腰直角三角形的面积较大。若飞行器位于三角形顶点上，在3架飞行器的基础上，每增加1架飞行器，飞行器之间所围成的空域面积相当于增加1个三角形面积。N架飞行器时，按等边三角形镶嵌排布的情况下，飞行器群所围成的空域面积达到安全飞行状态下的最小值，也就是飞行器之间互相无冲突时最紧密的排布情况。以该态势下N架飞行器在空域产生的平均能量为阈值当空域某时刻能量超过阈值，说明此时N架飞行器之间必然存在着冲突群现象，飞行器密度过大，应采取适当冲突解脱与流量控制手段保证飞行安全。

研究空域为120 km×120 km的正方形区域，飞行器水平方向最小安全间隔为10 km，以500 m为间隔将空域划分为若干正方形网格。以空域中的7架飞行器为例，初始时刻，飞行器按以10 km为边长的正三角形分布，如图6所示，线条表示飞行器运动方向。T= 0时刻，空域平均能量等于4.4 a.u.，该平均能量为7架飞行器无冲突飞行条件下所能达到的最大能量，若能量超过说明7架飞行器飞行密度过大，必然有互相影响的连环冲突，空域存在安全隐患。在进行冲突解脱的过程中，不能仅仅进行2架飞行器之间的冲突解脱，解脱策略必须考虑到涉及冲突的所有飞行器。图7表示飞行器运动过程中不同时刻整个空域能量的变化趋势，从图中可以看出，随着各个飞行器的不断分离，飞行器间距不断增大，空域平均能量也逐渐减小。

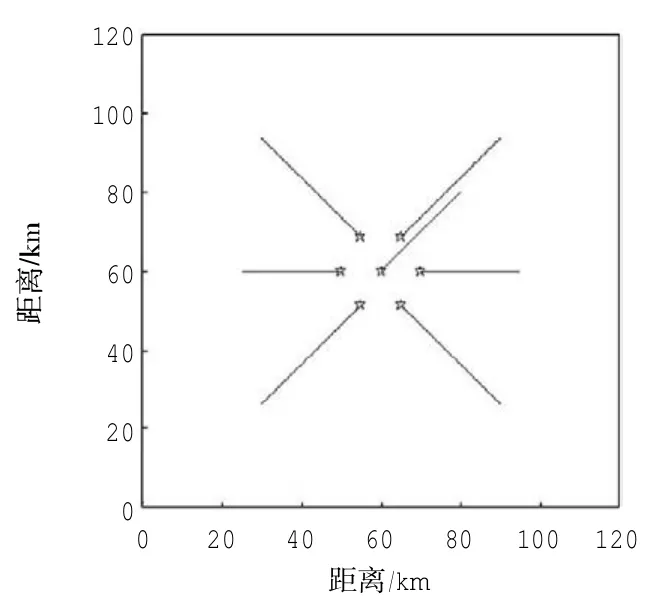
图6　7架飞行器飞行态势图Fig.6 Flight scenario of seven aircrafts

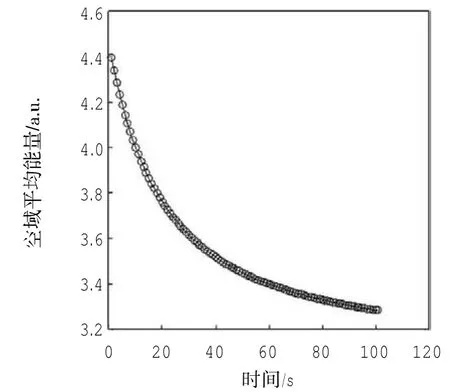
图7　不同时刻空域平均能量的变化Fig.7 Average energy change of airspace

通过仿真实验可以看出，若利用基于距离标准的传统冲突探测方法检测7架飞行器两两之间的飞行冲突，则最多需要进行次2架飞行器之间的冲突探测才能确定[10-11]。而本文所提方法不仅适用于飞行器与飞行器之间的短期冲突探测，而且能够同时关注到空域多架飞行器的飞行态势，快速实时地进行多机冲突群的探测。

4　结语

本文基于静电场理论提出一种适用于自由飞行空域的冲突探测方法。将空域中的飞行活动类比为点电荷，飞行活动之间的相互影响程度可以用点电荷之间的库仑力来表示，而系统的电势能则体现空域中飞行活动之间冲突的严重程度。该方法还具有关注空域中所有飞行活动形成的整体飞行态势，实时进行多架飞行器冲突群探测的能力。本文模型可进一步为自由飞行条件下冲突解脱算法提供依据和方案。

参考文献：

[1] Final Reportof RTCA Task Force 3- Free Flight Imp Lementation[R]. W ashington DC：RTCA Inc，1995.

[2] KUCHAR J，YANG L.A Review of conflict detection and resolution modelingmethods[J].IEEE Transon IntelligentTransportation Systems，2000，1（4）：179-189.

[3]李丹，崔德光.基于布朗运动的空中交通短期冲突探测[J].清华大学学报（自然科学版），2008，48（4）：477-481.

[4]刘小龙，罗以宁，赵喜求，等.一种改进的Prandini概率型中期冲突探测方法[J].计算机技术与发展，2013，1（23）：214-216.

[5]梁海军，杨红雨，肖朝，等.3维坐标系下的飞行冲突探测算法[J].四川大学学报（工程科学版），2013，45（2）：88-93.

[6] LIU W，HW ANG I.Probabilistic trajectory prediction and conflict detection for air traffic control[J].JournalofGuidance，Control，and Dyna-mics，2011，34（6）：1779-1789.

[7]蔡保平，杜乃珍.普通物理学[M].北京：化工工业出版社，2007：56-76.

[8] HU J.A Study of Conflict Detection and Resolution in Free Flight[D]. Berkeley：UniversityofCalifornia，1999.

[9]刘星，韩松臣.用于自由飞行冲突探测的Delaunay方法[J].数据采集与处理，2002，17（4）：446-449.

[10]靳学梅.自由飞行空域中多机探测与解脱技术研究[D].南京：南京航空航天大学，2004.

[11]周向华.冲突探测与解脱技术在未来空中交通管理中的应用[D].南京：南京航空航天大学，2009.

（责任编辑：杨媛媛）

Conflict detection for free flight using electrostatic approach

ZHANG Zhe，HUANG Xiaoxiao，W U Renbiao
（Intelligent Sigaland Image Processing Key Lab of Tianjin，CAUC，Tianjin 300300，China）

Abstract：A conflictdetection method for free flightbased on electrostatic theory is proposed.Flights in such an airspace usually have the freedom to choose routes and speeds，which elevates the complexity of flightenvironmentand conflict probability.The proposed method uses Coulomb force between point charges to evaluate severity of conflict between flights，while the potential system energy gives a global view of flight safety for the whole airspace.And ithas the intrinsic capability ofmulti-flight conflictdetection among flight clusters.Both conflict detection and conflict resolution in free flightoperation scenario can find benefitswith thismethod.

Key words：free flight；conflictdetection；electrostatic fieldmodel

作者简介：张喆（1982—），男，天津人，讲师，博士，研究方向为时频信号处理.

收稿日期：2015-03-05；修回日期：2015-04-30基金项目：国家科技支撑计划（2011BAH24B12）；中国民航大学科研启动基金项目（2011QD04S）

中图分类号：TP391；O441.4

文献标志码：A

文章编号：1674-5590（2016）01-0001-04