CF2ClC(O)OCH2CH3+OH的反应机理及动力学性质的理论研究

朱　鹏, 段雪梅, 刘靖尧

(吉林大学理论化学研究所, 长春 130021)



CF2ClC(O)OCH2CH3+OH的反应机理及动力学性质的理论研究

朱鹏, 段雪梅, 刘靖尧

(吉林大学理论化学研究所, 长春 130021)

摘要利用双水平直接动力学方法, 在MCG3-MPWB//M06-2X/aug-cc-pVDZ水平上研究了CF2ClC(O)OCH2CH3+OH的微观反应机理. 得到了反应物CF2ClC(O)OCH2CH3的5种稳定构象(RC1～RC5), 并对每一构象考察了发生在—CH3和—CH2—基团上的所有可能氢提取反应通道. 利用改进的变分过渡态理论(ICVT)结合小曲率隧道效应校正(SCT)计算了各反应通道的速率常数, 分析了各构象反应位点选择性. 结果表明, 对于构象RC1和RC2, 低温时氢提取反应主要发生在—CH2—基团上; 而对于构象RC3, RC4和RC5, 发生在—CH3基团上的氢提取反应通道在整个温度区间内占绝对优势. 根据Boltzmann配分函数计算总包反应速率常数, 在298 K温度下计算的体系总包反应速率常数与实验值相符, 进而给出200～1000 K温度范围内拟合了速率常数的三参数Arrhenius表达式: koverall=5.45×10-25T4.54exp(-685/T).

关键词直接动力学方法; 速率常数; 变分过渡态理论; 密度泛函理论; 反应机理

由于氟利昂(CFCs)对大气臭氧层的破坏以及引发温室效应已被禁止使用, 因此寻找环境友好型CFC替代物已成为实验和理论研究的热点. 近年来, 氟氯取代醚(HCFEs)[1,2]类化合物被认为是CFC新一代替代品, 已引起广泛关注. HCFE类化合物具有与CFC类似的物理化学性质, 且分子中的醚键能够提高其在对流层中的反应活性, 从而缩短其大气寿命. 氟氯取代脂(CFESs)是HCFE化合物降解的主要产物, 同时也是大气中重要的中间体. 由于降解产物CFES中含有氯原子, 释放氯原子进入同温层后仍会破坏臭氧层. 在大气中, CFES降解的主要途径是与OH自由基的反应, 因此, 为了更好评估CFES对大气环境的影响, 研究CFES与OH的反应机理及动力学性质是十分必要的.

本文主要关注CF2ClC(O)OCH2CH3与OH自由基的反应. 显然, 由于反应物CF2ClC(O)OCH2CH3含有较长的碳链, 因此通常具有不止一种稳定构象; 并且对于每个构象与OH的反应, 存在从2个反应位置(—CH3和—CH2—)发生的多条氢提取通道. 然而, 实验上Blanco等[3]使用相对速率方法只给出了该反应在298 K时的反应速率常数[(5.4±1.5)×10-13cm3·molecule-1·s-1], 而对于其它温度下的反应速率常数及反应位点选择性和产物分支比等信息均未见报道. 因此, 从理论上研究反应CF2ClC(O)OCH2CH3+OH的微观机理和动力学性质具有重要意义.

本文采用量子化学计算方法, 在MCG3-MPWB//M06-2X/aug-cc-pVDZ水平上, 得到了反应物CF2ClC(O)OCH2CH3的5个稳定构象, 并确定了与之相关的共23条不同的反应通道. 采用直接动力学方法[4～10], 应用变分过渡态理论(VTST)[11,12]在较大温度范围内计算了各条氢提取通道速率常数, 进而预测出总反应速率常数, 并分析每个构象反应位点的选择性及其对总反应的贡献; 此外, 在计算中利用等化学键反应估算了反应物和产物自由基的标准生成焓.

1计算方法

所有电子结构计算均采用Gaussian 09[13]程序完成. 在M06-2X/aug-cc-pVDZ[14]水平上优化各驻点的几何结构, 并通过频率分析确定反应物、产物和中间体为局部极小点, 而过渡态有唯一虚频. 通过内禀反应坐标(IRC)计算得到各反应通道的最小能量途径(MEP)确认过渡态连接了相应的反应物构象和产物. 在MEP上选取适当点进行频率分析, 获得所选点的梯度和海森(Hessian)矩阵. 为了获得更为准确的能量, 使用多系数外推的密度泛函方法MCG3-MPWB[15]计算了稳定点和MEP上4个非驻点的单点能量. 计算中采用0.9721作为M06-2X/aug-cc-pVDZ 的频率校正因子. MCG3-MPWB计算在结合Gaussian 03程序[16]的MLGAUSS 2.0程序[17]下完成.

采用变分过渡态理论结合内推单点能方法(ISPE)[18]获得体系双水平(MCG3-MPWB//M06-2X/aug-cc-pVDZ)势能面. 在此基础上, 利用改进的变分过渡态理论(ICVT)[19]结合小曲率隧道效应校正(SCT)[20,21]近似, 计算了每条反应通道的速率常数. 小曲率隧道校正方法假设最可几隧道效应路径是沿反应路径附近区域. 值得注意的是, 该反应体系中包含了2个重原子之间的轻粒子的迁移, 在低温区间大曲率隧道校正(LCT, Large Curvature Tunneling)可能更加重要. 然而, 由于LCT方法需要更加全面的势能面信息, 仅仅获得最小能量路径的信息是不够的, 因此受计算条件的限制, 目前还不能完成大曲率的计算; 另外, 对于类似的氢提取反应, 已有理论研究[22～28]表明利用SCT方法得到的反应速率常数值与实验结果相符. 因此, 本文对该反应体系采用SCT方法进行速率常数的计算. 在计算OH自由基的电子配分函数时, 考虑了由自旋轨道耦合引起的能级劈裂, 劈裂能级为140 cm-1. 所有动力学计算均采用Polyrate 9.7程序包[29]完成.

2结果与讨论

2.1稳定点的性质

由于反应物CF2ClC(O)OCH2CH3存在2个可以产生不同结构的转动, 通过对分子内基团的相对扭转, 可以得到不同构象. 以具有Cs对称性的优化结构RC1(见图1)为初始构象, 在M06-2X/aug-cc-pVDZ水平上得到了随二面角Cl—C—C—O和C—O—C—C变化的扫描势能曲线[图2(A), (B)]. 对扫描势能曲线上对应的极小点结构进行全优化后, 得到稳定构象RC2和RC3(图1). 从图2可见, 这2个过程的转换能垒分别约为0.96和5.15 kJ/mol. 为了确保得到所有可能的CF2ClC(O)OCH2CH3分子的稳定构象, 本文以构象RC3为基础, 得到了扭转二面角Cl—C—C—O的扫描势能曲线[图2(C)]. 从图2(C)可见, 势能曲线上还存在2个能量极小点, 经全优化后得到反应物构象RC4和RC5(图1). 在M06-2X/aug-cc-pVDZ水平下, RC3与RC4和RC5之间的旋转能垒分别约为0.46和0.71 kJ/mol. 在MCG3-MPWB//M06-2X/aug-cc-pVDZ水平下的计算结果表明, 反应物的5个构象中, RC2, RC4和RC5的能量接近, 其中RC4最稳定, RC2和RC5的能量仅比RC4分别高0.79和0.38 kJ/mol, 而RC1和RC3的能量比RC4分别高5.31和6.07 kJ/mol.

Fig.1　Optimized geometries parameters of conformers RC1—RC5 at the M06-2X/aug-cc-pVDZ level　Bond lengths are in nm and bond angles are in degree.

Fig.2　Torsional potential profiles for torsion angle Cl—C—C—O for RC1(A), torsion angle 　C—O—C—C for RC1(B) and torsion angle Cl—C—C—O for RC3(C)

在与OH自由基的反应中, H原子可以从CF2ClC(O)OCH2CH3中的—CH2—或—CH3基团上提取. 对于具有Cs对称性的构象RC1, 存在平面内氢(R1a)和平面外氢(R1b)两类氢原子, 其中—CH3和—CH2—基团中的两对面外H原子是等价的, 对反应的贡献以对称数的形式反映在总反应速率常数中, 因此, RC1有3条可区分的氢提取反应通道:

(R1a)

(R1b)

(R1c)

对于具有C1对称性的构象RC2—RC5, 由于—CH3和—CH2—基团上的全部5个H原子均不等价, 得到与之对应5条不同的氢提取反应通道:

(Rna, Rnb, Rnc)

(Rnd, Rne)

因此, 对于反应物CF2ClC(O)OCH2CH3的5个稳定构象, 我们共找到23条氢提取通道. 本文仅以能量最低的构象RC4为例, 图3给出了M06-2X/aug-cc-pVDZ水平上5条反应通道的过渡态及中间体的几何结构及相应的OH和H2O的实验值, 其它通道上驻点的结构及频率见图S1(见本文支持信息). 从图3可见, 过渡态构型中形成的键的伸长远大于相应断裂的键, 意味着过渡态都是和反应物相似的, 即“早垒”型过渡态. 如, 在TS4a中, 即将断裂的C—H键长比单独的反应物CF2ClC(O)OCH2CH3中的C—H键长伸长了9%, 而即将形成的H—O键长比H2O中H—O键长伸长了39%. 反应体系的其它氢提取过渡态具有与TS4a类似的结构特性. 此外, 由于反应物含有电负性较高的O原子和F原子, 因此在每条氢提取反应通道的入口和出口处都能找到氢键络合物, 这些络合物结构中, O…H和H…F的氢键距离均小于其范德华半径之和(0.272和0.267 nm), 其它键长则均很接近其在相应反应物或产物结构中的键长, 这表明CF3C(O)OCH2CH3+OH反应可能要经过一个间接的机理. 值得注意的是, 对于从—CH3和—CH2—基团上的氢提取反应通道, 由于OH自由基进攻H原子的位置和方向的不同, 所得到的产物具有不同的构象. 如, 从氢提取反应通道(R4d)和(R4e)分别得到了P4b和P4c 2种不同结构的产物自由基(见图3).

Fig.3　Optimized geometry parameters of reactants, products, transition-states, and hydrogen-bond 　complexes for the H-abstraction channels of R4 at the M06-2X/aug-cc-pVDZ　Bond lengths are in nm and angles are in degree.

2.2能量计算

精确的标准生成焓在评估反应热动力学性质和建立大气模型过程中十分重要. 由于在实验上缺少反应物和产物的标准生成焓值(ΔH{0—f,298), 因此, 使用等化学键反应(Ⅰ)～(Ⅲ)预测CF2ClC(O)OCH2CH3, CF2ClC(O)OCH2CH2和CF2ClC(O)OCHCH3的各构象的ΔH{0—f,298值[30,31].

(Ⅰ)

(Ⅱ)

(Ⅲ)

在MCG3-MPWB//M06-2X/aug-cc-pVDZ水平上得到了反应(Ⅰ)～(Ⅲ)中所有物种的几何构型、频率和能量, 然后计算出各反应的反应焓值, 再结合已知参考化合物的标准生成焓值[32](CH4: -74.89, CHF2Cl: -481.37, CH3F: -234.18, CF3Cl: -709.65, CH3: 145.65和CH3C(O)OCH2CH3: -445.22 kJ/mol)来计算反应物和产物自由基的各构象对应的标准生成焓值, 结果列于表1. 从表1可见, 对于构象RC1, 以及相应的产物自由基P1a, P1b和P1c, 其估算的标准生成焓分别为-838.47,-625.09, -628.02和-649.78 kJ/mol. 根据其余构象及其产物自由基与RC1及产物自由基之间焓值的差值, 很容易得到所有反应物构象和产物自由基的标准生成焓值.

Table 1　Standard enthalpies of formation(ΔH{0—f,298) at 298 K calculated at

图4为在MCG3-MPWB//M06-2X水平上反应CF3C(O)OCH2CH3+ OH的势能面示意图, 其中能量包含了零点能校正. 以(R4)反应的5条反应通道为例, 可以看到,各反应通道均为放热反应, 其中CH3上氢提取通道(R4a)～(R4c)的反应能为66.94 kJ/mol, 而—CH2—上氢提取通道由于产物构象不同反应能分别为-76.15和-88.70 kJ/mol. 反应首先经过反应前期的氢键络合物CR4a, CR4b, CR4c和CR4e, 相应的能量分别为-9.62, -5.86, -14.64和-7.53 kJ/mol, 其中, (R4c)和(R4d) 2条反应通道经由相同的反应前期络合物CR4c. 然后, 从络合物出发, 经过氢转移过渡态生成产物络合物, 进而分解得到产物自由基CF2ClC(O)OCH2CH2(P4a)或CF2ClC(O)OCHCH3(P4b和P4c)和H2O. 络合物CP4a, CP4b, CP4c, CP4d和CP4e分别比相应的独立产物稳定11.72, 7.95, 10.46, 11.72和5.86 kJ/mol. 从图4(D)可见, —CH3上的3个氢提取通道(R4a)～(R4c)和—CH2—上的2个氢提取通道(R4d)和(R4e)的反应能垒分别为9.20, 14.64, 6.28, 12.13和8.37 kJ/mol, 其中通道(R4c)能垒最低. 因此, 仅从能量角度分析, 预测对于构象RC4发生在—CH3基团上的氢提取反应更占优势, 是动力学上最可行的反应通道. 从图4(C)和(E)可见, 构象RC3和RC5具有类似的反应位置选择性. 与反应通道(R4)不同, 在图4(A)和(D)给出的构象RC1和RC2的各反应通道中, —CH2—上的氢提取通道在动力学和热力学上是最可行的, 是主要的反应通道. 如, 通道(R1c)的反应能垒为5.02 kJ/mol, 比—CH3上的氢提取通道(R1a)和(R1b)分别低了9.62和3.35 kJ/mol, 因此可以预测氢提取反应主要发生在构象RC1(或RC2)的—CH2—基团上.

Fig.4　Schematic potential energy profiles for the RC1+OH reaction(A), the RC2+OH reaction(B), the RC3+OH reaction(C), the RC4+OH reaction(D) and the RC5 + OH reaction(E)Relative energies with ZPE atthe MCG3-MPWB//M06-2X/aug-cc-pVDZ level are in kJ/mol.

2.3速率常数计算

在MCG3-MPWB//M06-2X/aug-cc-pVDZ水平上, 使用改进的变分过渡态理论结合小曲率隧道效应校正(ICVT/SCT)计算了全部23条氢提取反应通道在200～1000 K温度范围内的速率常数. 图5给出了RC4的主要反应通道(R4c)和(R4e)的TST, ICVT和ICVT/SCT速率常数曲线而其它稳定体反应通道的TST, ICVT和ICVT/SCT速率常数见图S2(见本文支持信息). 从图5(A)可见, 对于通道(R4c), 在298和500 K时,kICVT/kTST分别为0.92和0.93, 意味着变分效应在整个温度区间内起着一定作用, 且反应通道(R2c), (R3b), (R3c), (R3e), (R4a), (R4b), (R4d)和(R5c)也具有同样的变分效果. 而对于反应通道(R4e), 从图5(B)可见, 在整个温度区间范围内, TST曲线和ICVT曲线几乎完全重合, 即变分效应很小或可以被忽略. 通道(R1a), (R2a), (R2e), (R5b), (R5d)和(R5e)具有类似的变分效应. 另一方面, 从图5可见, 低温时ICVT/SCT速率常数远大于ICVT速率常数, 如, 反应通道(R4c)的kICVT/SCT/kICVT值在200, 500和1000 K时分别为8.9, 2.1和1.03, 这表明小曲率隧道校正在低温区间对这2个通道的速率常数计算中都起着重要作用. 其它各条氢提取反应通道都具有类似的隧道效应, 具体速率常数结果列于表S2(见本文支持信息).

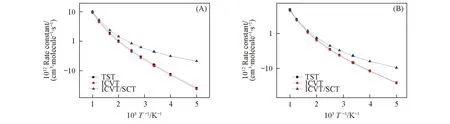
Fig.5　TST, ICVT and ICVT/SCT rate constants calculated at the MCG3-MPWB//M06-2X/aug-cc-pVDZ level 　versus 1000/T between 200 and 1000 K for path (R4c)(A) and for path (R4e)(B)

对每一稳定构象(RC1～RC5) 的总反应速率常数为与其所相应的氢提取反应通道速率常数之和, 即

k1=(k1a+k1b)+k1c=k1(—CH3)+k1(—CH2—)

kn=(kna+knb+knc)+(knd+kne)=kn(—CH3)+kn(—CH2—),n=2—5

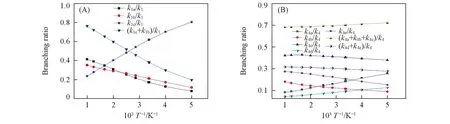
Fig.6　Plots of the calculated branching ratios versus 1000/T between 200 and 1000 K for the reaction RC1+OH→products(A) and the reaction RC4+OH→products(B)

图6(A)和(B)分别给出了RC1和RC4的各氢提取反应通道的产物分支比与温度的关系, 而其余稳定体的各氢提取反应通道的产物分支比与温度的关系在图S2(见本文支持信息)给出. 从图6(A)可见, 对于构象RC1, 在200 K时, 其所对应的的3条氢提取通道的产物分支比分别为0.08, 0.12和0.80, 随着温度的升高,k1c/k1比值下降, 而k1a/k1和k1b/k1比值上升, 当达到500 K时三者的比值分别为0.31, 0.29和0.40. 表明通道(R1c)在低温区间对构象RC1做主要贡献, 而随着温度的增加通道(R1a)和(R1b)的作用越来越大. 考虑到提取—CH3上的3个氢原子在实验上的不可分辨性, 本文给出—CH3基团上氢提取对构象RC1的总贡献k1(—CH3)/k1, 其中k1(—CH3)=k1a+k1b. 显然, 在低温时, 从—CH2—基团上的氢提取是反应的主要通道, 而随着温度的升高, 从—CH3基团上发生的氢提取通道对构象RC1贡献越来越大, 当T>380 K时成为主要的反应通道. 构象RC2具有与RC1类似的氢提取位置选择性. 图6(B)给出的RC4的各通道速率常数分支比随温度变化的关系与RC1不同. 在整个温度区间内, 发生在—CH3基团上的氢提取反应通道对构象RC4的贡献, 即k4(—CH3)=k4a+k4b+k4c占绝对优势, 而发生在—CH2—基团上的氢提取反应通道[kn(—CH2—)=k4d+k4e]对总反应的贡献较小. 构象RC3和RC5具有类似的反应位置选择性, 即—CH3基团上的氢提取是反应的主要通道.

反应CF3C(O)OCH2CH3+OH→产物的总包反应速率常数(koverall)由下式获得:

koverall=ω1k1+ω2k2+ω3k3+ω4k4+ω5k5

=ω1(k1a+k1b+k1c)+ω2(k2a+k2b+k2c+k2d+k2e)+ω3(k3a+k3b+k3c+k3d+k3e)+

ω4(k4a+k4b+k4c+k4d+k4e)+ω5(k5a+k5b+k5c+k5d+k5e)

=k1T+k2T+k3T+k4T+k5T

式中:ωn(n=1～5)为利用Boltzmann配分函数计算得到的所有构象对总包反应贡献的权重因子, 其表达式如下:

式中:R为理想气体常数, ΔEn为各构象RCn(n=1～5)与构象RC4的能量差. 表2给出了理论计算得出的速率常数和相应实验值. 在298 K时, 计算的双水平ICVT/SCT速率值为9.12×10-13cm3·molecule-1·s-1, 与实验值(5.4±1.5)×10-13cm3·molecule-1·s-1[3]相符. 由于实验未提供298 K以外其它温度的反应速率常数, 因此为了给实验研究提供参考, 本文拟合了koverall在200～1000 K温度范围内的三参数速率常数表达式, 即koverall= 5.45×10-25T4.54exp(-685/T).

Table 2Rate constants for each conformer and the overall rate constant[koverall/(cm3·molecule-1·s-1)] in the temperature range 200—1000 K at the MCG3-MPWB//M06-2X level

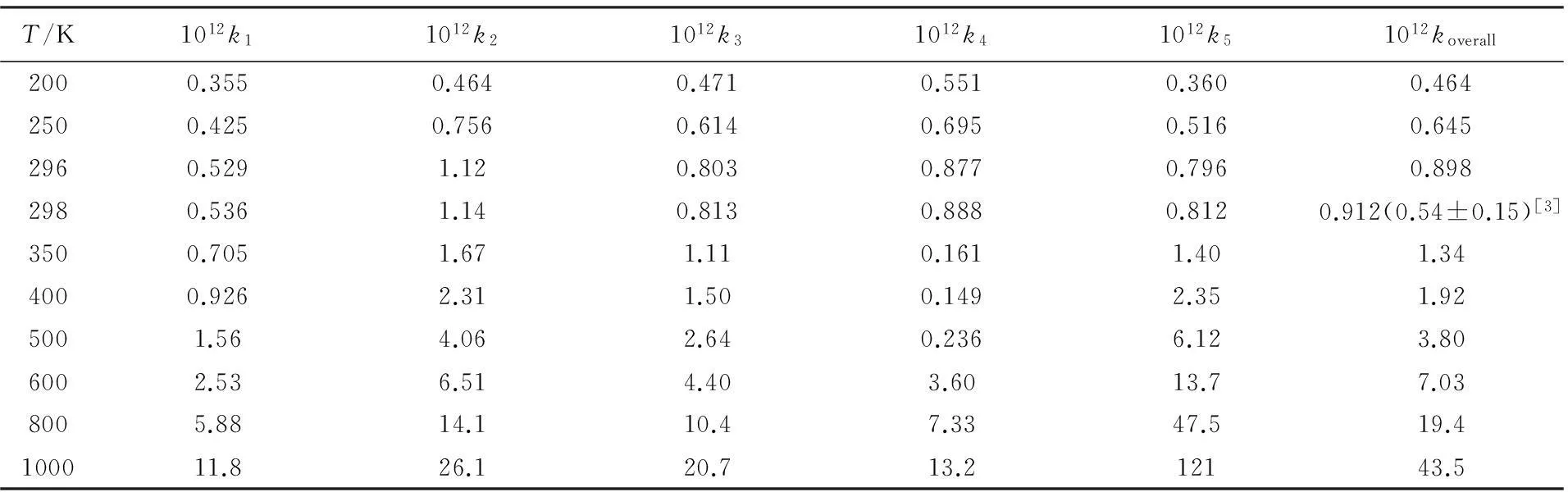
T/K1012k11012k21012k31012k41012k51012koverall2000.3550.4640.4710.5510.3600.4642500.4250.7560.6140.6950.5160.6452960.5291.120.8030.8770.7960.8982980.5361.140.8130.8880.8120.912(0.54±0.15)[3]3500.7051.671.110.1611.401.344000.9262.311.500.1492.351.925001.564.062.640.2366.123.806002.536.514.403.6013.77.038005.8814.110.47.3347.519.4100011.826.120.713.212143.5

Fig.7　Plot of the contributions of RC1, RC2, RC3, RC3 and RC4 to the reaction versus 1000/T between 200 and 1000 K

为了描述各构象对总反应的贡献, 图7给出了knT/koverall随温度变化的曲线. 从图7可见, 在200 K时k1T/koverall,k2T/koverall,k3T/koverall,k4T/koverall和k5T/koverall的比值分别为0.01, 0.31, 0.01, 0.45和0.22, 表明在低温区间构象RC4对总反应的贡献最大, 是最重要的反应物构象, 其次是构象RC2和RC5, 而构象RC1和RC3对总包反应的贡献可以忽略不计; 而随着温度的升高,k4T/koverall和k2T/koverall的比值下降,k5T/koverall的比值则升高, 特别是在400 K及更高的温度范围内,k5T/koverall的比值急速上升. 当T>500 K时, 各构象对总反应速率的贡献顺序为k5T/koverall>k2T/koverall>k4T/koverall>k3T/koverall>k1T/koverall, 表明在高温区间构象RC5对总反应速率具有决定性的贡献.

综上所述, 采用直接动力学方法, 研究了CF2ClC(O)OCH2CH3与OH自由基的反应的微观反应机理和动力学性质. 在M06-2X/aug-cc-pVDZ水平上确定了反应物的5个稳定的几何构象(RC1～RC5), 其中构象RC4为最稳定构象, RC2和RC5的能量接近. 由于这5个构象之间的能量差较小, 所以在动力学计算中它们对总反应速率的贡献应考虑在内. 对于每一个构象, 分别研究了发生在—CH2—和—CH3基团上的氢提取反应通道, 得到23条氢提取反应通道. 此外, 由于缺少关于反应物及产物自由基的标准生成焓数据, 用等化学键法估算了反应物及产物自由基的标准生成焓. 使用改进的变分过渡态理论结合小曲率隧道效应校正计算了各个氢提取通道在200～1000 K内的速率常数, 计算结果表明, 对于构象RC1和RC2, 氢提取反应在低温区间内主要发生在—CH2—基团上, 随着反应温度的升高, 发生在—CH3基团上的氢提取反应通道成为主要反应通道. 而对于构象RC3, RC4和RC5, 在整个温度区间内, 发生在—CH3基团上的氢提取反应通道都占绝对优势. 根据Boltzmann配分函数计算200～1000 K温度区间内总包反应的速率常koverall, 298 K的计算结果与实验值相吻合, 进而拟合了总反应在较大温度区间内的三参数的Arrhenius表达式:koverall=5.45×10-25T4.54exp(-685/T). 另外, 分析了5种构象对总包反应的贡献, 表明在低温区间构象RC4对总反应的贡献最大; 其次为RC2和RC5; 随着温度升高, 构象RC5的贡献变得越来越重要, 在高温区间对总反应贡献最大.

支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20150568.

参考文献

[1]Oyaro N., Sellevag S. R., Nielsen C. J.,Environ.Sci.Technol., 2004, 38, 5567—5576

[2]Sulback Andersen M. P., Nielsen O. J., Wallington T. J., Hurley M. D., DeMoore G. W.,J.Phys.Chem.A, 2005, 109, 3926—3934

[3]Blanco M. B., Teruel M. A.,Chem.Phys.Lett., 2007, 441, 1—6

[4]Hu W. P., Truhlar D. G.,J.Am.Chem.Soc., 1996, 118, 860—869

[5]Truhlar D. G., Garrett B. C., Klippenstein S. J.,J.Phys.Chem., 1996, 100, 12771—12800

[6]Truhlar D. G., Gordon M. S.,Science, 1990, 249, 491—498

[7]Tucker S. C., Truhlar D. G.,NewTheoreticalConceptsforUnderstandingOrganicReaction, Kluwer, Dordrecht, 1989, 291—346

[8]Truhlar D. G., Gordon M. S., Stechler R.,Chem.Rev., 1987, 87, 217—236

[9]Lu D. H., Truong T. N., Melissas V. S., Lynch G. C., Liu Y. P., Grarrett B. C., Stechler R., Issacson A. D., Rai S. N., Hancock G. C., Lauderdale J. G., Joseph T., Truhlar D. G.,Comput.Phys.Commum., 1992, 71, 235—262

[10]Garrett B. C., Truhlar D. G.,J.Phys.Chem., 1991, 95, 10374—10379

[11]Truhlar D. G., Garrett B. C.,Acc.Chem.Res., 1980, 13, 440—448

[12]Truhlar D. G., Garrett B. C.,Annu.Rev.Phys.Chem., 1984, 35, 159—189

[13]Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Mennucci B., Petersson G. A., Nakatsuji H., Caricato M., Li X., Hratchian H. P., Izmaylov A.F., Bloino J., Zheng G., Sonnenberg J. L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery J. A. Jr., Peralta J. E., Ogliaro F., Bearpark M., Heyd J. J., Brothers E., Kudin K. N., Staroverov V. N., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Rega N., Millam N. J., Klene M., Knox J. E., Cross J. B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R. E., Yazyev O., Austin A. J., Cammi R., Pomelli C., Ochterski J. W., Martin R. L., Morokuma K., Zakrzewski V. G., Voth G. A., Salvador P., Dannenberg J. J., Dapprich S., Daniels A. D., Farkas O., Foresman J. B., Ortiz J. V., Cioslowski J., Fox D. J.,Gaussian09,RevisionA.1, Gaussian Inc., Wallingford CT, 2009

[14]Zhao Y., Truhlar D.G.,Theor.Chem.Acc., 2008, 120, 215—241

[15]Zhao Y., Truhlar D. G., J.Phys.Chem.A, 2005, 109, 4209—4212

[16]Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Zakrzewski V. G., Montgomery J. A. Jr., Stratmann R. E., Burant J. C., Dapprich S., Millam J. M., Daniels A. D., Kudin K. N., Strain M. C., Farkas O., Tomasi J., Barone V., Cossi M., Cammi R., Mennucci B., Pomelli C., Adamo C., Clifford S., Ochterski J., Petersson G. A., Ayala P. Y., Cui Q., Morokuma K., Malick D. K., Rabuck A. D., Raghavachari K., Foresman J. B., Cioslowski J., Ortiz J. V., Boboul A. G., Stefnov B. B., Liu G., Liaschenko A., Piskorz P., Komaromi L., Gomperts R., Martin R. L., Fox D. J., Keith T., Al-Laham M. A., Peng C. Y., Nanayakkara A., Gonzalez C., Challacombe M., Gill P. M. W., Johnson B., Chen W., Wong M. W., Andres J. L., Gonzalez C., Head-Gordon M., Replogle E. S., Pople J. A,Gaussian03,RevisionA.1, Guassian Inc., Pittsburgh PA, 2003

[17]Zhao Y., Truhlar D. G.,MLGAUSS-Version2.0, University of Minnesota, Minneapolis, 2005

[18]Chuang Y. Y., Corchado J. C., Truhlar D. G.,J.Phys.Chem.A, 1999, 103, 1140—1149

[19]Garrett B. C., Truhlar D. G., Grev R. S., Magnuson A. W.,J.Phys.Chem., 1980, 84, 1730—1748

[20]Truhlar D. G.,J.Comput.Chem., 1991, 12, 266—270

[21]Liu Y. P., Lynch G. C., Truong T. N., Lu D. H., Truhlar D. G., Garrett B. C.,J.Am.Chem.Soc., 1993, 115, 2408—2415

[22]Galano A., Alvarez-Idaboy J. R., Ruiz-Santoyo M. E., Vivier-Bunge A.,Chem.Phys.Chem, 2004, 5, 1379—1388

[23]Taghikhani M., Parsafar G. A., Sabzyan H.,J.Phys.Chem.A, 2005, 109, 8158—8167

[24]Wang Y. X., Gao H., Wang Q., Liu J. Y.,Chem.J.ChineseUniversities, 2010, 31(6), 1240—1245(王永霞, 高红, 王钦, 刘靖尧. 高等学校化学学报, 2010, 31(6), 1240—1245)

[25]Ren H., Zhang L. L., Wang R. S., Pan X. M.,J.Phys.Chem.A, 2012, 116, 10647—10655

[26]Jin T. Y., Wang Q., Liu J. Y.,Chem.J.ChineseUniversities, 2013, 34(3), 641—649(金铜音, 王钦, 刘靖尧. 高等学校化学学报, 2013, 34(3), 641—649)

[27]Zhu P., Ai L. L., Wang H., Liu J. Y.,Comput.Theor.Chem., 2014, 1029, 91—98

[28]Zhu P., Duan X. M., Liu J. Y.,J.Fluorine.Chem., 2015, 176, 61—70

[29]Corchado J. C., Chuang Y. Y., Fast P. L., Hu W. P., Liu Y. P., Lynch G. C., Nguyen K. A., Jackels C. F., Ramos A. F., Ellingson B. A., Lynch B. J., Melissas V. S., Villa J., Rossi I., Coitino E. L., Pu J., Albu T. V., Steckler R., Garrett B. C., Isaacson A. D., Truhlar D. G.,POLYRATE,Version9.7, University of Minnesota, Minneapolis, 2007

[30]Jin X. H., Hu B. C., Jia H. Q., Lu C. X.,Chem.J.ChineseUniversities, 2013, 34(7), 1685—1690(金兴辉, 胡炳成, 贾欢庆, 吕春绪. 高等学校化学学报, 2013, 34(7), 1685—1690)

[31]Wang H. X., Wang B. Y., Zhang J. L., Li Z. R., Li X. Y.,Chem.J.ChineseUniversities, 2011, 32(5), 1123—1128(王海霞, 汪必耀, 张俊玲, 李泽荣, 李象远. 高等学校化学学报, 2011, 32(5), 1123—1128)

[32]Linstrom P. J., Mallard W. G.,NISTChemistryWebbook, http://webbook.Nist.Gov/chemistry

Mechanism and Kinetics of the Hydrogen-abstraction Reaction of

CF2ClC(O)OCH2CH3with OH Radicals†

ZHU Peng, DUAN Xuemei, LIU Jingyao*

(InstituteofTheoreticalChemistry,JilinUniversity,Changchun130021,China)

AbstractThe mechanism of the hydrogen abstraction reaction of CF2Cl(O)OCH2CH3+OH was studied theoreticallyviaa dual-level direct dynamics method at the MCG3-MPWB//M06-2X/aug-cc-pVDZ level. Five stable conformers(RC1—RC5) of the reactant CF2Cl(O)OCH2CH3were located, and for each conformer, the possible H-abstraction channels from —CH3and —CH2— groups were taken into account. The rate constants were calculated using the improved canonical variational transition-state theory(ICVT) with the small-curvature tunneling correction(SCT) and the selectivity of the reaction sites of CF2Cl(O)OCH2CH3was evaluated. The results show that for the conformers RC1 and RC2, the H-abstraction reactions mainly take place at the —CH2— group at low temperature, while for the conformers RC3, RC4 and RC5, the hydrogen abstraction from the —CH3group is the major channel in the whole considered temperature range. The overall rate constant is obtained by considering the weight factors of the five conformers calculated from the Boltzmannn distribution function. It is found, that the calculatedkoverallat 298 K is in good agreement with the available experimental data. The three parameter expression for the overall reaction within 200—1000 K is fitted tokoverall=5.45×10-25T4.54exp(-685/T).

KeywordsDirect dynamics method; Rate constant; Variational transition-state theory; Density functional theory; Reaction mechanism

(Ed.: Y, Z)

† Supported by the National Natural Science Foundation of China(No.21373098).

doi:10.7503/cjcu20150522

基金项目：国家自然科学基金(批准号: 21373098)资助.

收稿日期:2015-07-20. 网络出版日期: 2015-12-20.

中图分类号O641; O643

文献标志码A

联系人简介: 刘靖尧, 女, 博士, 教授, 博士生导师, 主要从事化学反应动力学研究. E-mail: ljy121@jlu.edu.cn