有限维修能力下作战单元时变可用度评估模型*

徐　立，李庆民，李　华，邵松世

(1.海军工程大学 兵器工程系， 湖北 武汉　430033； 2.海军工程大学 科研部， 湖北 武汉　430033)



有限维修能力下作战单元时变可用度评估模型*

徐立1，李庆民2，李华1，邵松世2

(1.海军工程大学 兵器工程系， 湖北 武汉430033； 2.海军工程大学 科研部， 湖北 武汉430033)

摘要：针对作战单元任务期内备件需求随任务阶段动态变化的现实情况，考虑作战单元因携行维修能力有限而导致可修件具有一定报废概率的影响，通过引入报废因子，建立两级保障体制下，故障件具有一定报废概率且不考虑外部补给的作战单元时变可用度评估模型。采用ExtendSim仿真软件进行计算，根据仿真值进行参数拟合得到模型中报废因子的近似解析表达形式。研究表明，报废因子能够适应不同的可靠性维修性参数值，模型具有较强的适应性。该模型有效解决了备件非平衡状态下的装备时变可用度评估问题，可为装备管理人员制定合理的保障方案提供支撑。

关键词：作战单元；时变可用度；备件；报废概率；评估模型

作战单元是独立执行作战任务的基本单元，其执行的任务具有时间长、类型复杂等特点，要求装备具备较高的可用度。同时，受作战单元设备维修能力和人员技术水平的限制，不能对装备部件的所有故障模式进行维修，从而造成备件损耗。当作战单元远离后方保障基地，备件补给困难且运输成本过高时，作战单元需要依靠自身维修保障能力开展自主保障，携行备件的损耗将会大幅降低装备的作战效能。因此，在存在备件损耗的前提下，如何对携行备件方案进行合理评估是装备管理人员亟待解决的难题。

作战单元通常由一个保障单元和数个战斗单元组成，构成两级保障组织，如海上舰船编队等。战斗单元主要担负战斗任务，保障单元为战斗单元提供伴随保障。目前，关于两级保障系统的维修保障，国内外通常采用METRIC理论开展相关研究。Sherbrook[1]于1968年首次提出METRIC模型，在此基础之上，Slay[2]和Muckstadt[3]将原模型进行扩展，提出了适合多等级多层级维修保障系统的VARI-METRIC模型，该模型一经提出便在空军[4-5]、海军[6-7]和民航[8]等领域得到了广泛应用。对于传统METRIC模型和VARI-METRIC模型，其适用于长期稳态过程，面向装备全寿命周期；而对于装备执行作战任务，备件需求变化较大，以上模型难以解决此类问题。针对有限任务时长，任务阶段复杂多变的情况，Slay等[9]与王睿等[10]基于Dyna-METRIC理论分别建立了适合空军和海军的装备可用度评估模型；Lau等[11-12]基于动态帕尔姆定理建立了战损和系统钝化条件下的装备时变可用度评估模型；刘勇等[13]在认为保障系统能够对故障件完全可修的前提下，建立了存在排队等待的装备时变可用度评估模型；张建军等[14]，将BCMP排队模型引入作战单元的维修保障过程，建立了备件保障度评估模型。这些模型都是建立在部件完全可修的基础之上，部件的报废会影响备件平衡，给评估造成较大误差。针对维修保障过程中备件并不总是“修复如新”的问题，谭林等[15]在考虑不完全维修的前提下兼顾部件退化失效，建立了串联系统的可用度模型；周伟等[16]考虑备件需求的相关性，建立了稳态条件下可修复系统的备件配置模型。

对于执行长期任务的作战单元，如舰船编队等，执行任务远离岸基保障基地，受编队本身维修能力和战场前送补给能力的限制，备件损耗不能够得到有效的补充，之前的模型无法给出精确的解析解；若要对每个任务阶段进行仿真求解将会浪费大量时间，影响该方法的可操作性。针对此类问题，构建作战单元备件具有报废概率的时变可用度评估模型，并采用仿真的方法对该模型进行验证。

1问题描述

对于由一个保障单元和数个战斗单元构成的两级保障组织，战斗单元主要执行战斗任务，除此之外本身具备一定的备件库存和维修能力；保障单元对应多个战斗单元，具有相对较强的维修补给能力，作战单元的结构组成如图1所示。当装备故障之后，定位引起故障的现场可更换部件(Line Replaceable Unit，LRU)，若战斗单元能够修理该部件，则在战斗单元进行修理，修理完成的部件送至本单元仓库作为备件储存；若不能在本单元修理，则将此故障件送至保障单元进行修理，同时向保障单元的备件仓库申请一个备件，而故障件在保障单元具有一定的维修概率，修复件送至保障单元备件仓库储存，作为备件使用，若部件不能修理，则部件作为报废件处理。维修保障过程中，不考虑后方基地的补给，部件仅可能在保障单元确定是否报废。整个周转过程如图2所示。

图1　作战单元保障组织结构Fig.1　Support structure of combat units

图2　故障件维修保障过程Fig.2　Process for support of invalid parts

在模型搭建过程中，以传统METRIC模型族的一般假设为假设条件[2]。

1)故障件的到达符合泊松分布，不同故障单元的故障相互独立；

2)每个战斗单元的库存检测采用连续的(S-1,S)策略，即向保障单元送修一件的同时申请一件；

3)不考虑各战斗单元之间的横向补给，备件只能由战斗单元向保障单元送修、申请；

4)故障件的维修符合先到先修原则，不考虑维修等待；

5)故障件维修后修复如新，故障件维修时间服从指数分布。

2作战单元装备时变可用度评估模型

2.1单元备件需求率

备件需求率与部件的故障间隔时间(Mean Time Between Failures, MTBF)及装备利用率UR有关。若装备利用率随时间变化，则时刻t记装备利用率为UR(t)；若单个装备包含该部件的数量为QPM，装备数量为Nsys，则时刻t备件需求率DR(t)的计算公式为：

(1)

对于战斗单元的某一特定装备系统，其装备数量有限，已坏的装备不能再次产生故障，在计算需求率时，应剔除此类情况，在文献[11]中此类现象被称为钝化。可将整个任务期T划分为n等份，即时刻t=1,2,3,…,n。假设在划分的时间区间内，装备利用率和正在工作的装备数量为恒值。记保障单元的编号为0，战斗单元的编号为j=1,2,3，…,J。装备由K个LRU部件组成，编号为k=1,2,3,…,K。时刻t，钝化情况下，可产生备件需求的装备数量为：

Nsysj(t)=Nsysj·A(t-1)

(2)

其中：Nsysj为战斗单元j装备的实际配置数量；A(t-1)为t-1时刻的装备系统可用度,在t=0时刻A(0)=1。

则此时在战斗单元j，部件k的需求率为：

(3)

其中，QPMk为部件k在系统中的装配数量。

由于战斗单元的维修能力有限，故障件有一定的不可修概率，则该单元向本级备件仓库提出的有效需求率为：

λjk(t)=DRjk(t)·(1-NRTSjk)

(4)

其中，NRTSjk为部件k在战斗单元j的不可修概率。

保障单元对备件k的需求量为各战斗单元对保障单元的备件需求量之和，时刻t，保障单元备件k的需求率为：

(5)

2.2期望短缺数EBO函数

2.2.1动态帕尔姆定理

(6)

若维修时间服从均值为TAT的指数分布，令Y表示故障件的服务时间；若仅考虑站点维修，则故障件在t>τ时可以修复的概率为：

(7)

则可得在t>τ时刻部件不能修复的概率为：

(8)

时刻t，在修件均值为：

(9)

若考虑站点之间的运输时间TPT，令维修时间为X，总的服务时间为维修时间和运输时间之和，即Y=X+TPT，则站点在t时刻的可修复概率为：

(10)

类似地，可得在时刻t，在修件均值为：

(11)

2.2.2站点备件期望短缺数的计算

根据作战单元维修保障过程，受保障单元维修能力的限制，记备件的报废概率为SP。同时，由于得不到上级保障组织的供应和维修支持，报废备件在整个任务过程中可视为始终停留在维修渠道中(METRIC理论中，将备件的维修保障流程形象地称为备件供应渠道；维修渠道用来表示备件的维修过程；备件维修渠道数则为正在进行维修的备件数量)，在保障单元维修渠道中的备件数量由两部分构成：部件在修件数量；报废件的等效数量。其中等效数量应理解为报废件对整个维修保障系统所施加的影响。部件k在保障单元的维修渠道数均值为：

E[P0k(t)]=E[RP0k(t)]+E[CD0k(t)]

(12)

其中：E[·]表示变量均值；P0k(t)为时刻t保障单元部件k的正在处理的数量；RP0k(t)为时刻t保障单元部件k的在修件数量；CD0k(t)为保障单元在时刻t的部件k的累积报废数量。

由于部件故障符合泊松分布，根据动态帕尔姆定理可知，时刻t，保障单元部件k的维修渠道数量均值为：

(13)

其中：TAT0k为部件k在保障单元的维修时间均值；TPTjk表示由保障单元向战斗单元j补给部件k的延误时间；SP0k为该部件在保障单元的报废概率。

动态帕尔姆定理适用于修理时间具有平稳分布的情况。而对于报废件，其不存在修复时间或修理时间可视为整个任务周期，因此部件累积报废数量均值的求解不符合动态帕尔姆定理的适用条件。为了使报废件数量均值的求解近似符合动态帕尔姆定理，引入报废因子f(SP0k)，其为报废概率的函数，表征备件报废对维修渠道数的影响。在时间t，故障件在一定报废概率下的维修渠道数可等效为：

(14)

由泊松分布的性质可得在时刻t，保障单元备件k的库存量为s0k时，其备件供应短缺数为：

(15)

同理由动态帕尔姆定理可得，时刻t战斗单元j在修部件k数量的均值为：

(16)

其中：RPjk(t)为时刻t，战斗单元j,部件k的维修渠道数；TATjk为部件k在战斗单元j的维修时间均值。

时刻t，由保障单元向战斗单元j运输的备件数量期望值为：

(17)

其中：OSPjk(t)为时刻t，战斗单元j与保障单元之间备件k的订购补给渠道数量；TPT0k为保障单元向战斗单元j运输的时间，为恒值。

战斗单元j的供应渠道数由三部分组成：自身站点的备件维修渠道数；战斗单元与保障单元的订购补给渠道数；由于保障单元该项备件短缺造成的补给延误。其均值为:

(18)

其中，fjk(t)为时刻t战斗单元j的需求占保障单元总需求的比例，可表示为：

(19)

可得战斗单元j在时刻t，备件库存为sjk时的备件短缺数为：

(20)

2.3作战单元装备时变可用度评估模型

对于单个站点，当故障件更换时间忽略不计时，战斗单元装备可用度主要取决于现场更换单元LRU备件短缺数的大小。对于组成中具有串联结构的系统，任何部件空缺即会导致装备停机。当备件短缺数确定以后，可得装备在任务周期内的任意时刻t的可用度为：

(21)

对于作战单元而言，在时刻t装备的整体可用度为[4]：

(22)

3算例分析

在可用度评估模型的建模过程中，由于报废因子的具体表达式未知，该表达式的求解成为亟待解决的问题。在动态帕尔姆定理的基础之上，要对该因子的具体表达形式进行理论推导较为困难。搭建仿真模型，在同等条件下进行过程仿真，得到一定参数下的作战单元可用度值，然后再根据可用度值，在文中搭建的可用度解析模型框架之下，对报废因子进行拟合求解成为解决问题的一种方式。

以作战单元为研究对象，取单个部件平均故障间隔时间MTBF=600 h。采用离散时间仿真软件ExtendSim对单部件的维修保障过程进行建模仿真,搭建模型如图3所示，其中图(a)表示部件维修保障仿真主程序，包含多个功能单元及模块，如保障单元包含维修模块和备件库存模块，对应战斗单元1模块和战斗单元2模块；图(b)表示图(a)中的战斗单元的功能模块及其连接关系，包含备件申请延误模块、部件运行模块、战斗单元维修模块和部件当机判断模块。

取报废概率分别为0.1,0.3,0.5,0.7进行仿真计算，在每一个方案下独立运行1000次，间隔一定的时间取平均值即为所得样本点，得到不同报废概率下的装备可用度值如图4～7黑色星点所示。图4表示在保障单元部件报废概率为0.1时，该部件在整个任务周期内的可用度的变化趋势；图5,图6,图7分别表示在同等保障参数下，报废概率分别为0.3,0.5和0.7时，该部件在整个任务周期的可用度的变化趋势。

(a) 部件维修保障过程仿真主程序(a) Chief simulation program for process of support system

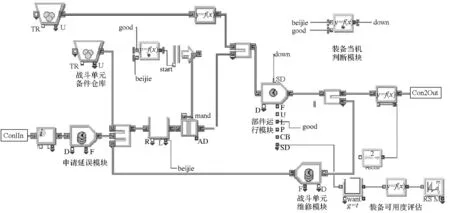
(b) 图(a)中战斗单元模块(b) Module of fight unit in figure (a)图3　ExtendSim仿真程序Fig.3　Simulation program based on ExtendSim

如果将报废因子设为维修时间、运输时间、任务时间的函数，则需为函数的准确性做大量仿真实验，给求解验证工作造成困难。为了研究的方便，假设报废因子仅是关于报废率SP0的函数。根据图4～7中仿真样本进行参数拟合得到报废因子的近似解析表达式为f(SP0k)=SP0k·(8.5e-10SP0k+1.7e-1.46SP0k)。在此报废因子之下，结合第2节的时变可用度评估模型，求得各时刻的可用度值，如图4～7中的实线所示。在报废概率的影响之下，装备随着时间的推移可用度逐渐递减；在实际的保障过程中，随着工作时间的推移，装备可用度逐渐降低，证明评估模型符合现实规律。当报废概率为0.1时，仿真得到的可用度值误差较大，计算结果与仿真结果的吻合度较差，这主要与仿真过程存在一定的随机性有关。随着报废概率的增加，仿真值与解析值的误差范围较小，此时计算结果与仿真结果具有较好的吻合度，表明了计算结果在报废概率较高时具有很强的适用性。

图4　报废概率为0.1时的装备可用度Fig.4　Availability of equipment when scrap probability is 0.1

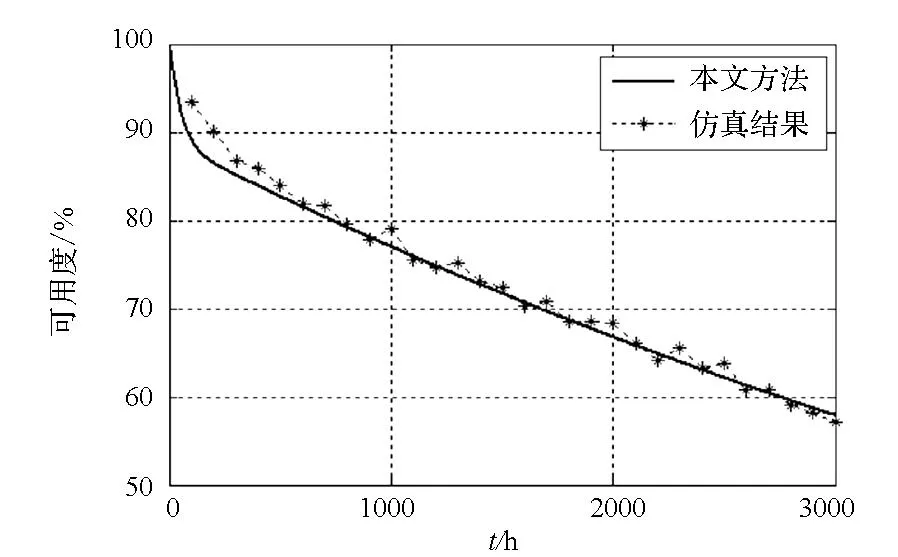
图5　报废概率为0.3时的装备可用度Fig.5　Availability of equipment when scrap probability is 0.3

图6　报废概率为0.5时的装备可用度Fig.6　Availability of equipment when scrap probability is 0.5

图7　报废概率为0.7时的装备可用度Fig.7　Availability of equipment when scrap probability is 0.7

根据此报废因子，改变维修性保障性参数和任务时长，得到相应的可用度值，并与仿真值进行对比，见表1。在维修周转时间与部件平均故障间隔时间之比较低时，如战斗单元的维修时间为72 h，运输时间为48 h，中继级维修时间为48 h时，此时周转时间与故障间隔时间之比为0.28，计算得到的误差较低，误差水平保持在1%左右。随着维修周转时间与平均故障间隔时间比值的升高，如维修时间分别增长到144 h和288 h，运输时间增长到96 h和192 h，此时周转时间与平均故障间隔时间之比分别为0.56和1.12；当维修周转对装备可用度的影响逐渐升高时，解析方法和仿真方法的误差有逐渐变大的趋势，但最大误差在3%以下，而在采用仿真方法进行可用度计算时本身也存在一定的误差，因此该误差值在可接受范围内，说明了报废因子一定范围内具有较强的适应性，所建模型具有较强的可信度。为了进一步验证模型的准确性，进行如下算例。

表1　部件相关参数及计算结果对比

一个保障单元和四个战斗单元构成的作战单元结构如图8所示，任务阶段内装备利用率见表2，装机数分别为2,1,1,2。

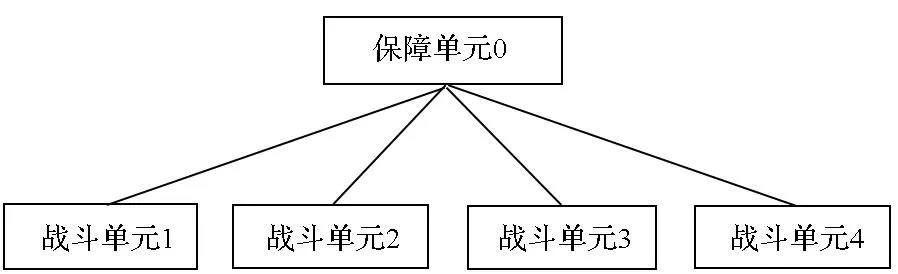
图8　作战单元保障组织结构Fig.8　Support framework of combat unit

各单元备件配置方案如表3所示；各部件的可靠性参数及费用见表4；维修性参数见表5。

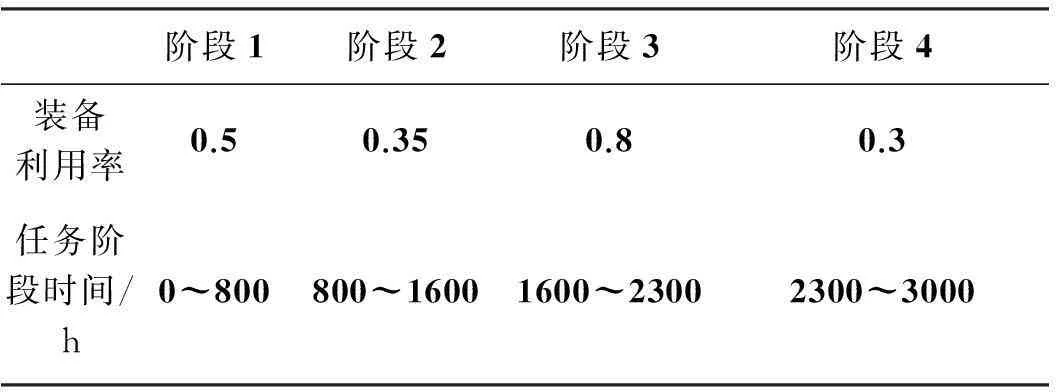
表2　装备运行方案

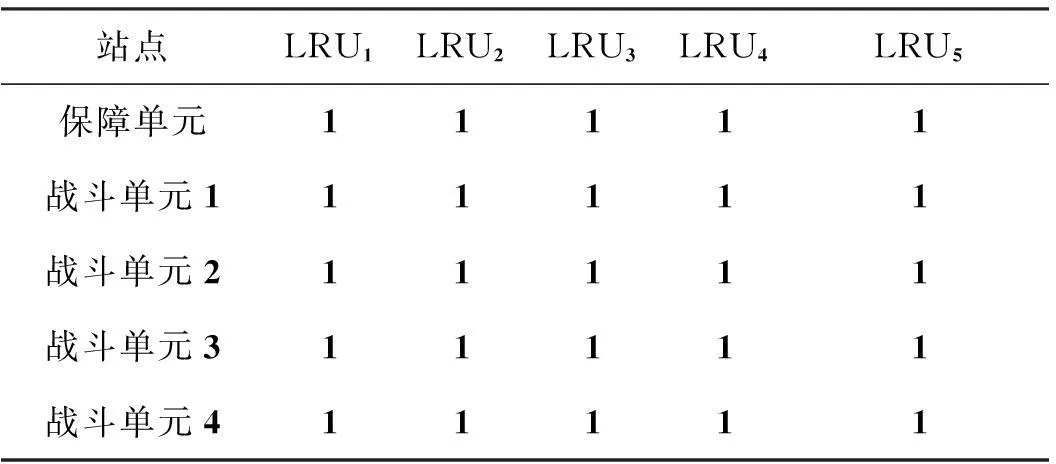
表3　各单元备件配置方案

表4　装备部件的相关参数

可得装备可用度随时间的变化曲线如图9所示，由该图可知，随着工作时间的增长，在任务阶段内，可用度逐渐降低，这是由于随着时间的推移，备件报废的数量逐渐增多，可用备件数量逐渐减少。在相同的算例下取与仿真值(如图9中星点标记)进行对比，二者相差不大，具有较高的一致性。模型能够在作战单元备件处于非平衡状态时合理评估装备可用度，为装备管理方制定备件配置方案提供理论支持。根据可用度仿真值进行报废因子近似解析表达式的求解，并将该表达式进行推广的方法较为合理。该方法在解决此类模型框架已经确定，但部分表达式与相应参数的关系不明确的问题时可类似采用。

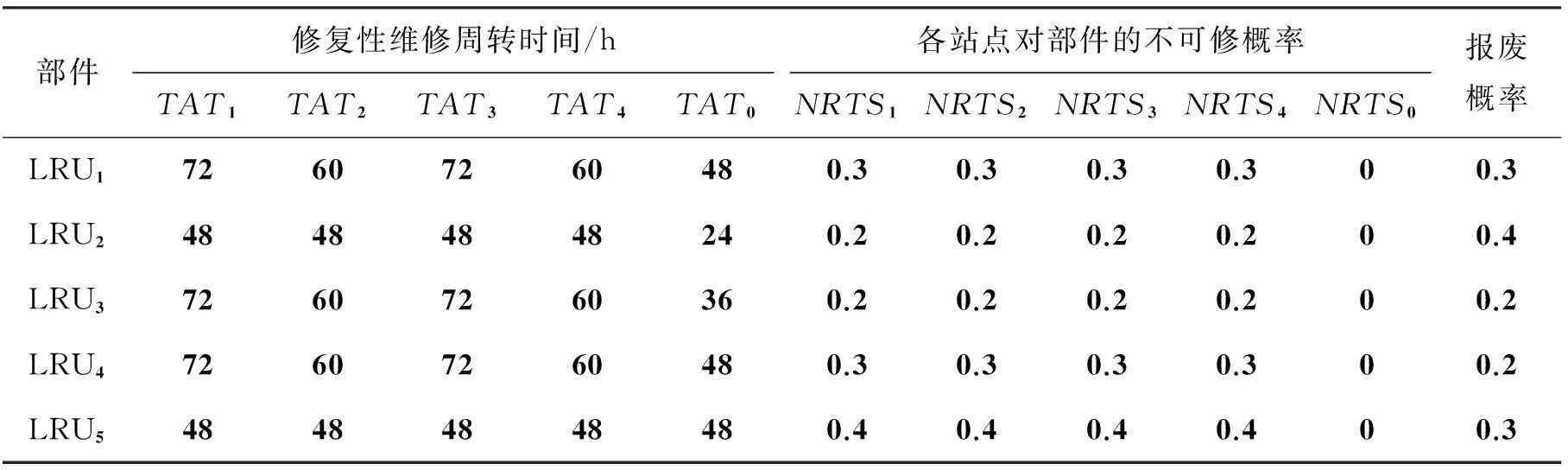
表5　装备部件维修性参数

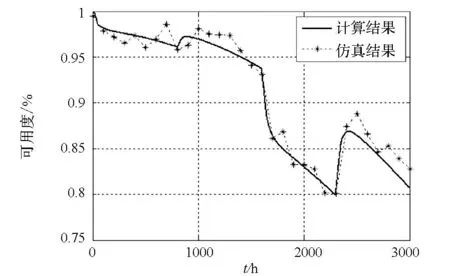
图9　装备时变可用度对比Fig.9　Comparison for time-varying availability of equipment

4结论

1)以任务周期内作战单元装备维修保障活动为背景，考虑单元维修能力的限制，通过引入报废因子建立有限维修能力下的作战单元装备时变可用度模型，拓展了传统任务单元可用度评估模型中备件完全可修的前提条件。

2)通过搭建ExtendSim仿真模型对保障方案进行评估，得到装备可用度仿真值，并对报废因子进行参数拟合，得到报废因子的近似解析表达式。算例分析表明该因子在不同可靠性维修性参数下也具有较好的适用性。

3)模型在评估任务各阶段装备系统可用度时与仿真值误差较小，具有运算方便，准确度高的优点，能够为舰船编队等作战单元的装备管理人员制定任务期内的备件携行方案提供决策支持。

参考文献(References)

[1]Sherbrooke C C. METRIC: a multi-echelon technique for recoverable item control[J]. Operations Research, 1968, 16(1): 122-141.

[2]Slay F M. VARI-METRIC: an approach to modeling multi-echelon resupply when the demand process is Poisson with a gamma prior[R]. Washington DC,USA: Logistics Management Institute, 1984.

[3]Muckstadt J A. A model for a multi-item, multi-echelon, multi-indenture inventory system[J]. Management Science, 1973, 20(4): 472-481.

[4]Sherbrooke C C. VARI-METRIC: improved approximations for multi-indenture, multi-echelon availability models[J]. Operations Research, 1986, 34(2): 311-319.

[5]阮旻智，彭英武，李庆民，等. 基于体系保障度的装备备件三级库存方案优化[J]. 系统工程理论与实践, 2012，32(7)：1623-1630.

RUAN Minzhi, PENG Yingwu, LI Qingmin, et al. Optimization of three-echelon inventory project for equipment spare parts based on system support degree[J]. Systems Engineering—Theory & Practice, 2012, 32(7): 1623-1630. (in Chinese)

[6]Rustenburg W D, Van Houtum G J, Zijm W H M. Spare parts management at complex technology-based organizations: an agenda for research[J]. International Journal of Production Economics, 2001, 71(1-3): 177-193.

[7]阮旻智，李庆民，黄傲林. (R,Q)库存策略下消耗件的协同订购方案优化[J]. 北京理工大学学报, 2013,33(7): 680-684.

RUAN Minzhi, LI Qingmin, HUANG Aolin. Optimization of cooperative ordering project for consumable spare parts under (R,Q) inventory policy[J]. Journal of Beijing Institute of Technology, 2013, 33(7): 680-684. (in Chinese)

[8]Costantino F, Gravio G D, Tronci M. Multi-echelon, multi-indenture spare parts inventory control subject to system availability and budget constraints[J]. Reliability Engineering & System Safety, 2013, 119: 95-101.

[9]Slay F M, Bachman T C, Kline R C, et al. Optimizing spare support: the aircraft sustainability model[R]. Washington,USA: Logistics Management Institute, 1996.

[10]王睿，雷红伟，彭英武，等. 战时任务条件下舰艇装备多级备件优化[J]. 上海交通大学学报, 2013，47(3): 398-403.

WANG Rui, LEI Hongwei, PENG Yingwu,et al. Optimization of warship spare parts in the scenario of wartime mission[J].Journal of Shanghai Jiaotong University, 2013，47(3): 398-403.(in Chinese)

[11]Lau H C, Song T C, See C T, et al. Evaluation of time-varying availability in multi-echelon spare parts systems with passivation[J]. European Journal of Operational Research, 2006, 170(1): 91-105.

[12]Lau H C, Song T C. Evaluation of time-varying availability in multi-echelon inventory system under combat damage[C]//Proceedings of IEEE International Conference on Automation Science and Engineering， 2005： 226-231.

[13]刘勇，武昌，李阳,等. 两级备件保障系统的装备时变可用度评估模型[J]. 兵工学报, 2010,31(2)：253-256.

LIU Yong, WU Chang, LI Yang, et al. Evaluation model of equipment time-varying availability in two-echelon spare support system[J]. Acta Armamentarii,2010, 31(2)：253-256. (in Chinese)

[14]张建军，刘芳，张涛，等．基于BCMP排队网络的作战单元备件保障度评估模型[J]．兵工学报，2009,30(1)：110-113.

ZHANG Jianjun, LIU Fang, ZHANG Tao, et al. The model of combat unit spares availability based on BCMP queuing network[J]. Acta Armamentarii,2009,30(1)：110-113. (in Chinese)

[15]谭林，程志军，郭波．考虑不完全维修的可修串联系统可用度模型[J]．国防科技大学学报，2009, 31(6)：100-105.

TAN Lin，CHENG Zhijun，GUO Bo．Availability of series repairable systems under imperfect repair[J]．Journal of National University of Defense Technology, 2009, 31(6)：100-105. (in Chinese)

[16]周伟，蒋平，刘亚杰，等．考虑需求相关的可修复系统备件配置模型[J]. 国防科技大学学报，2012,34(3)：68-73．

ZHOU Wei, JIANG Ping, LIU Yajie, et al．A spare allocation model for repairable systems considering correlated spare demands[J]. Journal of National University of Defense Technology, 2012, 34(3): 68-73. (in Chinese)

Evaluation model of time-varying availability for combat units under finite repair capacity

XULi1,LIQingmin2,LIHua1,SHAOSongshi2

(1.Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China;2. Office of Research and Development， Naval University of Engineering, Wuhan 430033, China)

Abstract：Aimed at the demand of spare parts changes dynamically as the mission phases change, and considering the influence of the scrap probability owing to the finite carrying repair capacity of combat units, by the introduction of the scrap factor, the evaluation model of time-varying operation availability for two echelon support system was developed, in which, the failure parts can be scrapped and there is no exterior supply. And then, a simulation is realized based on the ExtendSim software and the availability results was received. According to the results, the parameter fitting was carried into execution and the approximate analytical formula of scrap factor in the availability model was obtained. In a given example, the scrap factor can adapt to different reliability and maintainability parameters, and the adaptability is validated. The evaluation model is a complementary for conventional models which is developed based on the spare parts balance in support system and can help equipment personals to make appropriate spare parts programs.

Key words：combat units; time-varying availability; spare parts; scrap probability; evaluation model

中图分类号：E911; TJ83

文献标志码：A

文章编号：1001-2486(2016)01-114-08

作者简介：徐立(1987—)，男，湖北荆门人，博士研究生，E-mail：xuli123948@163.com；李庆民(通信作者)，男，教授，博士，博士生导师,E-mail:licheng001@hotmail.com

基金项目：国家部委基金资助项目(51304010206,51327020105)

*收稿日期：2015-02-06

doi:10.11887/j.cn.201601019

http://journal.nudt.edu.cn