碳纤维增强聚合物基复合材料频率选择表面的电磁传输特性*

李长亮，鞠　苏，陈大庆，陈　勇，任明利，张天斌

(1. 太原卫星发射中心 技术部， 山西 太原　030027； 2. 国防科技大学 航天科学与工程学院， 湖南 长沙　410073)



碳纤维增强聚合物基复合材料频率选择表面的电磁传输特性*

李长亮1,2，鞠苏2，陈大庆1，陈勇1，任明利1，张天斌1

(1. 太原卫星发射中心 技术部， 山西 太原030027； 2. 国防科技大学 航天科学与工程学院， 湖南 长沙410073)

摘要：为了避免采用金属频率选择表面制备的天线罩中存在的热残余应力和弱黏接界面等问题，采用与聚合物基复合材料罩壁结构相容性好的碳纤维增强聚合物基复合材料制备频率选择表面，利用自由空间法对试样的电磁传输性能进行测试，并采用数值分析模型对碳纤维复合材料频率选择表面的电磁传输机制和电磁传输影响因子进行分析。结果表明：碳纤维复合材料频率选择表面具有频率选择功能，但谐振频率处的电磁传输损耗较大；通过改变复合材料频率选择表面的单元缝隙率、厚度、电导率以及介电常数可以实现对其电磁传输性能的调节。

关键词：频率选择表面；复合材料；碳纤维；数值分析；电磁传输

频率选择表面(Frequency Selective Surface，FSS)属于无源阵列周期型结构，它是由相同的单元在二维方向上以特定间隔排列构成的无限大阵列，属于空间滤波器范畴。FSS可以实现电磁波的频率选择和极化选择，其频选特性主要决定于谐振单元的类型、尺寸、排布方式和其周围的介质材料。按照与电磁波相互作用的结果，可以将FSS分为带通型和带阻型两类。带通型(也称为孔径型)FSS[1-2]通过在金属屏上周期性开孔，可以允许通带内的电磁波透过，同时反射频率在通带外的电磁波。带阻型(也称为贴片型)FSS通过在介质表面上布满周期性金属贴片，实现与带通型FSS相反的电磁传输特性。基于FSS的频选电磁传输特性，其被广泛应用于隐身天线罩[3-5]的设计和制备中。

传统的FSS隐身天线罩是金属FSS(铝制或铜制)和天线罩罩体结构的结合[5-9]。罩体结构一般为陶瓷基复合材料或聚合物基复合材料，它们的热膨胀系数与金属不同，并且与金属的黏接界面性能较差。天线罩在服役过程中，经常会面临恶劣的外部环境，如先进战术导弹的飞行马赫数多在4以上，地地导弹的再入速度甚至超过12马赫，因此，导弹上的天线罩一般工作在500～2400 ℃范围内，且再入大气层时某些导弹表面的热变化率达到了540～820 ℃/s左右，导致导弹天线罩罩壁结构存在巨大的温度梯度和较高的热应力。对于卫星或飞船天线罩来说，会受到高低温交变、太阳辐照和粒子辐照等恶劣环境的考核。因此，服役过程中金属FSS天线罩不可避免地存在热失配、弱黏接等问题。当采用多层金属FSS级联实现多频谐振时，异质层黏接界面带来的问题会更加突出。

碳纤维增强聚合物基复合材料具有轻质高强和良好的导电性等特点[10]，通过合理的铺层设计还可以使其与复合材料罩体结构具有相近的热膨胀系数，并且其与复合材料罩体结构具有优良的黏接性能。因此，采用碳纤维增强聚合物基复合材料设计并制备FSS，可望改善金属FSS天线罩中存在的热残余应力和弱黏接界面等问题。

1碳纤维复合材料FSS的制备及电磁传输性能的测试

1.1原材料

采用的基体为LT-5089环氧树脂体系，增强材料为1K的T300平纹布，采用真空袋压工艺制备碳纤维增强环氧树脂复合材料。为了测量复合材料的等效电导率，将试样切割为7 mm×60 mm的长方形条，通过绝缘双面胶带将其固定在一块绝缘板上，采用导电银胶(OTS-9050)对试样端部进行包裹[11]。采用阻抗分析仪测量试样的电阻，最终测得碳纤维复合材料纤维方向的等效电导率为9600 S/m。

1.2试样制备

图1　碳纤维复合材料十字形缝隙FSS试样Fig.1　Specimen of carbon composite FSS with four-legged slot array

采用三维雕刻技术在碳纤维复合材料板上制备十字形缝隙阵列，制备的FSS试样尺寸为196 mm×196 mm×0.15 mm，如图1所示。复合材料FSS的单元尺寸参数描述和取值分别见图2和表1。

图2　十字形缝隙FSS的单元尺寸参数Fig.2　Dimensional parameters of four-legged slot array FSS

尺寸参数值/mmw0.6Fa14.0Fb11.0

1.3电磁传输性能测试

采用自由空间法[12]进行复合材料FSS电磁传输性能的测试，它包括两个聚焦天线(发射天线和接收天线)、夹持试样的工装、网络分析仪(Agilent 8720 ET network analyzer)以及数据处理系统，如图3所示。测试频率设为10 GHz～20 GHz，电磁波为垂直极化方式，电场方向与纤维方向一致，测试过程中入射电磁波始终保持垂直入射。

图3　自由空间测试系统Fig.3　Free space measurement system

测试结果表明，复合材料FSS可以实现频率选择功能，但在谐振频率处的电磁传输损耗，即最小传输损耗高于4 dB，如图4所示。为了降低碳纤维复合材料FSS的最小传输损耗，将进一步通过数值计算的方法对其电磁传输机制以及电磁传输影响因子进行分析。

图4　十字形缝隙复合材料FSS的电磁传输曲线Fig.4　Electromagnetic transmission characteristics of composite FSS with four-legged slot array

2碳纤维复合材料FSS电磁传输性能的数值分析

2.1数值模型的建立和验证

在CST微波工作室中建立碳纤维复合材料FSS的数值计算模型，入射电磁波为平面波，电磁波电场方向为-y方向，x和y方向的边界条件设置为周期性边界，z方向边界条件设置为开放边界，材料类型设置为正交各向异性，如图5所示。利用该仿真模型计算得到的碳纤维复合材料FSS的电磁传输特性见图4。由图4可知：实验测得的碳纤维复合材料FSS的谐振频率与最小传输损耗分别为12.95 GHz和4.03 dB，相应的数值计算结果分别为13.4 GHz和3.72 dB，二者在总体变化趋势上是一致的。实验结果与仿真结果的均方根误差为1.0 dB，为测试频率范围内传输损耗变化幅度的6.3%，因此，建立的仿真模型可以有效地评估复合材料FSS的电磁传输性能。实验结果与计算结果的差别主要是由FSS试样的阵列有限性以及复合材料表面电阻的非均匀性引起的[13]，前者在数值计算时被认为是不存在的，也就是仿真模型在阵列方向是无限大的。

2.2碳纤维复合材料FSS的电磁传输机制

图6～8分别为碳纤维复合材料FSS在谐振频率(13.52 GHz)处的电场、电能量密度和电流密度分布。由图6和图7可知：电磁波主要通过长度方向与电场方向垂直的矩形缝隙进行传播。当电磁波靠近复合材料FSS时，电磁波能量开始向单元缝隙聚集，待通过单元缝隙后能量又逐渐分散。由图8可知：虽然电磁波发射端口处电场方向为-y方向，但FSS上的电流方向以x方向为主，且电流都集中在对传输电磁波能量起主要作用的缝隙周围。

(a) xy平面(a) xy plane

(b) xz平面(b) xz plane图6　碳纤维复合材料FSS的电场分布Fig.6　Electric field distribution of composite FSS

(a) xy平面(a) xy plane

(b) xz平面(b) xz plane图7　碳纤维复合材料FSS的电能量密度分布Fig.7　Electric energy density distribution of composite FSS

2.3单元尺寸参数对碳纤维复合材料FSS电磁传输特性的影响

单元间隔固定时，单元的缝隙率由缝隙宽度w和缝隙长度Fb决定。如图9所示，缝隙宽度w由0.6 mm增大到2.2 mm的过程中，FSS的最小传输损耗由4.2 dB降低至0.9 dB，而谐振频率的变化范围为13.39 GHz～13.92 GHz。如图10所示，当缝隙长度Fb由9.8 mm增加至10.6 mm时，复合材料FSS的谐振频率由15.01 GHz降低至13.99 GHz，最小传输损耗则由4.7 dB减小为4.0 dB。因此，提高缝隙率虽然可以降低复合材料FSS的最小传输损耗，但会引起FSS谐振频率发生漂移。

(a) x方向(a) x direction

(b) y方向(b) y direction图8　碳纤维复合材料FSS的电流密度分布Fig.8　Current density distribution of composite FSS

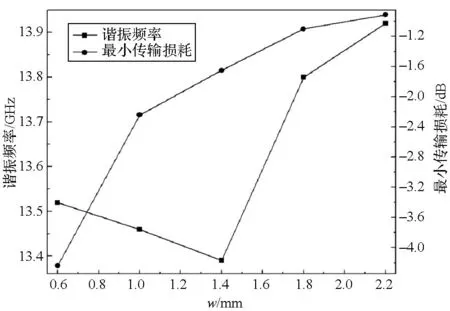
图9　缝隙宽度w对复合材料FSS的谐振频率与最小传输损耗的影响Fig.9　Effects of the dimensional parameter w on resonant frequency and minimum transmission loss of the composite FSS

如图11所示，在复合材料FSS的厚度由0.15 mm增大至3.0 mm的过程中，其谐振频率由13.52 GHz变为13.55 GHz，因此，无介质加载的复合材料FSS的谐振频率对其厚度不敏感。最小传输损耗随着厚度的增加先减小后增大，当厚度由0.15 mm增大至1.35 mm时，最小传输损耗由4.24 dB减小至最小值1.69 dB。当厚度大于1.35 mm时，FSS的最小传输损耗开始逐渐增大，但增大的趋势比较缓慢。

图10　缝隙长度Fb对复合材料FSS的谐振频率与最小传输损耗的影响Fig.10　Effects of the dimensional parameter Fb on resonant frequency and minimum transmission loss of the composite FSS

图11　厚度对复合材料FSS谐振频率与最小传输损耗的影响Fig.11　Effects of the thickness on the resonant frequency and the minimum transmission loss of the composite FSS

2.4材料参数对碳纤维复合材料FSS电磁传输性能的影响

在图12中，C1，C2和C3分别为复合材料垂直于电场方向、平行于电场方向以及厚度方向的电导率，单位为S/m。由图12可知，材料的电导率对FSS的谐振频率影响很小，主要影响其最小传输损耗；增大垂直于入射电磁波电场方向的材料电导率C1可以显著降低复合材料FSS的最小传输损耗；当C1和C2分别从9.0×103S/m提高到1.0×107S/m时，FSS的最小传输损耗分别降低3.12 dB和0.6 dB，二者之和小于C1和C2同时化引起的最小传输损耗的变化量(3.99 dB)，说明C1和C2对最小传输损耗的影响存在交互效应；C3对复合材料FSS的最小传输损耗没有影响。

(a) C1和C2的影响(a) Effects of C1 and C2

(b) C3的影响(b) Effects of C3图12　电导率对复合材料FSS电磁传输性能的影响Fig.12　Effects of the electrical conductivities of composite materials on the electromagnetic transmission characteristics of the composite FSS

与金属材料不同，复合材料通过改性、添加填料或铺层等方式可以使其介电常数在一定范围内变化，因此通过改变介电常数降低复合材料FSS最小传输损耗是工程可实现的。E1，E2和E3分别为复合材料FSS垂直于电场方向、平行于电场方向以及厚度方向的介电常数。图13～15为E1，E2和E3单独变化时，FSS的电磁传输曲线。由图可知：E1，E2和E3单独变化时，谐振频率变化很小；当E1和E2分别由1.0增大到9.0时，FSS的最小传输损耗分别增加了0.3 dB和2.3 dB；当E3由1.0增大到9.0时，FSS的最小传输损耗降低了0.8 dB。因此，虽然改变介电常数E3可以降低FSS的最小传输损耗，但效果不明显。

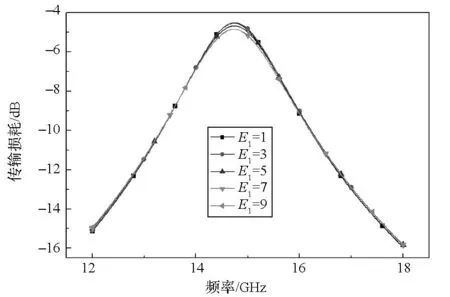
图13　E1对复合材料FSS电磁传输性能的影响Fig.13　Effects of E1 on electromagnetic transmissioncharacteristics of the composite FSS

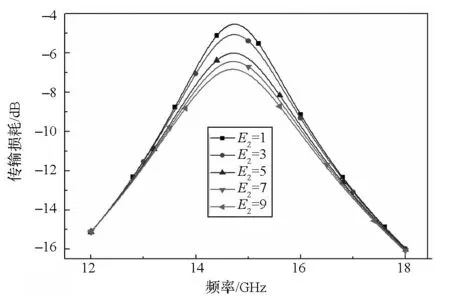
图14　E2对复合材料FSS电磁传输性能的影响Fig.14　Effects of E2 on electromagnetic transmissioncharacteristics of the composite FSS

图15　E3对复合材料FSS电磁传输性能的影响Fig.15　Effects of E3 on electromagnetic transmissioncharacteristics of the composite FSS

3结论

在10 GHz～20 GHz内，制备的碳纤维复合材料FSS可以实现频率选择功能，但其谐振频率处的传输损耗较大。为进一步降低碳纤维复合材料FSS的最小传输损耗，采用有限积分法对碳纤维复合材料FSS的传输机制进行了研究，通过单参数仿真实验，得到了影响复合材料FSS最小传输损耗的因素：

1)入射电磁波通过FSS时存在一个“先聚集，再发射”的过程，电磁波主要通过长度方向与电场方向垂直的缝隙进行传播；

2)提高复合材料FSS的单元缝隙率可以降低其最小传输损耗，但单元缝隙长度和宽度的变化同时会导致复合材料FSS谐振频率的漂移；

3)提高复合材料的面内电导率，尤其是垂直于入射电磁波电场方向的电导率，可以显著降低复合材料FSS的最小传输损耗，且电导率的变化对谐振频率不会产生影响；

4)通过改变材料的介电常数可以降低复合材料FSS的最小传输损耗，但效果不明显。

参考文献(References)

[1]Bozzi M, Perregrini L, Weinzierl J, et al. Efficient analysis of quasi-optical filters by a hybrid MoM/BI-RME method[J]. IEEE Transactions on Antennas & Propagation, 2001, 49(7): 1054-1064.

[2]Bayatpur F, Sarabandi K. Multipole spatial filters using metamaterial-based miniaturized-element frequency-selective surfaces[J].IEEE Transactions on Microwave Theory & Techniques, 2008, 56(12):2742-2747.

[3]Kim P C,Lee D G. Composite sandwich constructions for absorbing the electromagnetic waves[J]. Composite Structures, 2009, 87(2):161-167.

[4]Kim P C, Lee D G, Seo I S, et al. Nanocomposite stealth radomes with frequency selective surfaces[J]. Composite Structures, 2008, 86(s1-3): 299-305.

[5]Kim P C, Lee D G, Seo I S, et al. Low-observable radomes composed of composite sandwich constructions and frequency selective surfaces[J]. Composite Science and Technology, 2008, 68(9): 2163-2170.

[6]Costa F, Monorchio A. A frequency selective radome with wideband absorbing properties[J]. IEEE Transactions on Antennas & Propagation, 2012, 60(6):2740-2747.

[7]Kim P C, Chin W S, Lee D G, et al. EM characteristics of the RAS composed of E-glass/epoxy composite and single dipole FSS element[J]. Composite Structures, 2006, 75(s1-4): 601-609.

[8]Choi I, Jin G K, Lee D G, et al. Aramid/epoxy composites sandwich structures for low-observable radomes[J]. Composites Science & Technology, 2011, 71(14):1632-1638.

[9]Widenberg B. A general mode matching technique applied to band pass radomes[R]. Technical Report: LUTEDX/(TEAT-7098), 2001.

[10]Rinker M, Gutwinski M, Schauble R. Experimental and theoretical investigation of thermal stress in CFRP foam core sandwich structures[C]// Proceedings of the 13th International Conference on Composite Materials, Stockholm, Sweden, 2005.

[11]Kim I T, Tannenbaum A, Tannenbaum R. Anisotropic conductivity of magnetic carbon nanotubes embedded in epoxy matrices[J]. Carbon, 2011, 49(1): 54-61.

[12]Chung D D L. Electromagnetic interference shielding effectiveness of carbon materials[J]. Carbon, 2001, 39(2): 279-285.

[13]Liu H T, Cheng H F, Chu Z Y. Absorbing properties of frequency selective surface absorbers with cross-shaped resistive patches[J]. Materials and Design, 2007, 28(7): 2166-2171.

Electromagnetic transmission characteristics of frequency selective surfaces with carbon fiber fabric/epoxy composite

LIChangliang1,2,JUSu2,CHENDaqing1,CHENYong1,RENMingli1,ZHANGTianbin1

(1. Technical Department, Taiyuan Satellite Launch Center, Taiyuan 030027, China；2. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：There are problems, such as thermal residual stress and second bonding layers, in radome which is prepared by metal FSSs (frequency selective surfaces). To avoid these disadvantages, carbon fiber fabric/epoxy composite which has good compatibility with radome wall structure of polymer composite was adopted to prepare FSSs; the free space method was carried out to evaluate the electromagnetic transmission characteristics of the composite FSS specimens; the numerical analysis model was employed to analyze the electromagnetic transmission mechanism and influencing factors of FSS. Results show that: the composite FSS with carbon fiber can realize the function of frequency selection, while the transmission loss at the position of resonance frequency is great; the electromagnetic transmission performance of composite FSS can be adjusted by changing the aperture-to-cell ratio, thickness, conductivity and dielectric constant.

Key words：frequency selective surface; composite; carbon fiber; numerical simulation; electromagnetic transmission

中图分类号：TN95

文献标志码：A

文章编号：1001-2486(2016)01-050-06

作者简介：李长亮(1986—)，男，河北衡水人，工程师，博士，E-mail：nudt_tslc@163.com;鞠苏(通信作者)，男，讲师，博士，E-mail:suju-nudt@nudt.edu.cn

基金项目：国家自然科学基金资助项目(11202231)；国防科技大学校预研基金资助项目(JC12-01-07)

*收稿日期：2015-07-23

doi:10.11887/j.cn.201601009

http://journal.nudt.edu.cn