基于最大树理论的分阶段相量测量单元配置方案

徐 岩 应璐曼 王增平（新能源电力系统国家重点实验室（华北电力大学） 保定 071003）



基于最大树理论的分阶段相量测量单元配置方案

徐 岩 应璐曼 王增平
（新能源电力系统国家重点实验室（华北电力大学） 保定 071003）

摘要当前相量测量单元（PMU）配置主要采用启发式算法进行，不足之处在于无法实现不完全可观下分阶段配置PMU，也无法同时保证N-1故障下可观性和经济性。为此，提出一种分阶段配置PMU并保证N-1条件下可观性的优化PMU配置方案。该方案首先依据通信质量、经济效益和均衡性三方面对广域电网进行分区，再按照熵理论对各区内节点脆弱性指标进行排序，以这两方面为基础采用最大树理论实现全网PMU分区分阶段配置。最后，设计了N-1条件下全网可观的PMU配置方案，为现实条件下的PMU配置工作提供了坚实的理论基础。以IEEE 39节点系统对所述方案进行测试，其结果表明本方案不但在经济性、安全性和时间效益方面取得了较好的平衡，而且对于现有电网中已装配PMU的情况，本方法具有更好的效果。

关键词：相量测量单元配置 分阶段 最大树理论 N-1条件

国家自然科学基金（50777016）和中央高校基本科研业务费专项资金（12MS110）资助项目。

Staged Phasor Measurement Unit Placement Algorithm Based on Theory of Maximum Tree

Xu Yan Ying Luman Wang Zengping
（State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Baoding 071003 China）

Abstract The phasor measurement unit (PMU) placement schemes based on heuristic method are widely applied nowadays. However, these algorithms fail to place PMU by steps in an incomplete observable power system, and also fail to fit the observability and economy in N-1 fault at the same time. So an optimized scheme of staged PMU placement which can ensure the observability in N-1 fault is discussed in this paper. Firstly, the wide system is divided into zones by communication, economic benefit and balance. Then the vulnerability index of each node in the zones is sorted according to entropy. Hence, the theory of maximum tree is used in the zonal and phased placement of PMU. At last, PMU placement is checked and added to fit the observability in N-1 case. The test on IEEE 39-node system shows the economy, security and time-efficiency of the proposed method. Moreover, compared with other PMU placement algorithms, the scheme has better performance on the condition that PMUs have been already placed in real system.

Keywords：Phasor measurement unit placement, by steps, the theory of maximum tree, N-1 condition

0 引言

相量测量单元（Phasor Measurement Unit，PMU）利用全球定位系统（Global Positioning System，GPS）信号同步采集次秒级的模拟电压、电流信号，得到电压和电流信号的幅值和相位，并将其传送到调度中心的数据集中器，在调度中心可以得到整个电网的同步相量，以供实时监测、保护和控制等使用，被认为是电力系统未来最重要的测量设备[1,2]。因此，从电力系统监测角度考虑，如何以PMU的最少配置实现全网的完全可观测是当前较为重要的研究课题之一。

现有的实现可观性的PMU配置的方法，主要采用启发式方法，包括模拟退火（SA）、遗传算法[3]、禁忌搜索（TS）[4]、粒子群优化（PSO）[5]和最小生成树[6]等。这些方法最大的不足在于收敛速度慢，需要很长的执行时间，并且难以获取全局最优解，限制了它们在实际大型电力系统中的应用。

很多研究表明，在电网中若要实现系统的完全可观，需要在1/4到1/3的网络节点上配置PMU[7]。在广域电网中，一次性进行大规模的PMU配置并不可行，必须分阶段实现其配置。据此，本文提出一种基于最大树理论的分阶段PMU配置，根据电网PMU阶段配置的目标规划，选取阶段性最需要配置的关键节点进行PMU安装，这种方案不仅使得每个阶段性配置的效益最大，而且保证了配置数量尽可能少。本方案采用的PMU配置方案主要分以下四个步骤进行：首先，将庞大的广域电网进行系统分区；其次，对区域内所有节点的脆弱性指标进行评估和排序；然后，根据每个阶段区域内PMU配置数量的规划，进行基于最大树原理的PMU配置；最后，在实现系统完全可观后，重点探讨脆弱性元件发生N-1故障时PMU的再配置[8]。

1 PMU配置基础

1.1 系统分区

分区方案中区域的大小、区域的数目和各PMU从属的区域对广域后备保护的性能都有很大影响[9]。本文主要将分区通信质量Tmax[10,11]、分区经济效益CΣ[12]和各区均衡性S作为权衡指标（对以上三个指标的分析说明详见附录）[13]。

对于不同的分区方案，应该按这三个指标选择总体最优的方案。以上三个指标的单位各不相同，须首先统一量纲，设归一化后对应的结果分别为和S*，则目标函数为

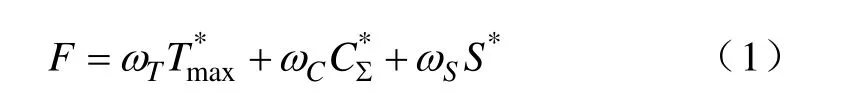
根据式（1）所定义的目标函数，采用遗传算法，可实现对大电网的分区，在各不同区域内，根据其实际情况（如当地电力安全重要程度、经济水平等），可进行符合当地情况的PMU配置规划；另一方面，各个区域间PMU配置相互关联较小，可同时展开，有利于增强配置效率。

1.2 区域内脆弱性节点评估

电力系统作为一个能量平衡系统，其内部的稳定平衡可以通过系统内部能量分布的熵变过程来描述[14]。本文采用直流潮流法预测当某个节点受到扰动后对系统能量分布变化（即潮流熵）产生的影响，用以衡量该节点的脆弱程度。具体推导见附录第3节。从而得到节点的脆弱性指标

式中，ΔEa为节点受到单位扰动对系统的潮流冲击，ΔEa越大，节点a扰动对系统的冲击越大；HD(a)为系统承受节点扰动时的潮流冲击分布规律，HD(a)越小，系统的潮流冲击分布越集中。

根据式（2）与附录第3节，仅通过全网线路参数，即可初步估计各节点脆弱性指标。对电网进行PMU配置规划时，优先对未配置且脆弱性大的节点进行PMU配置，有利于增强电网的强壮性。

1.3 基于图论的PMU配置规则

1.3.1 不完全可观阶段的最大树配置规则

在未实现PMU完全可观前，本文利用图论的一些知识，根据PMU的配置规则，引入一种适合工程上使用的最大树算法。

最大树的概念：设G=(V, E)是连通图，T是G的生成树，用E（ T）表示T的枝集，用e（ T）表示E（ T）中枝的数量，用T（ G）表示G的全部生成树的集。若有且仅有一个T*∈T( G)，对任意的T∈T( G)，都有e（ T*）＜e（ T），则称T*为G的最大（生成）树[15]。

将最大树的方法引入电网，就是对局部配置PMU之后生成的电网树的分析，深化对寻优规则的理解和操作，进行PMU的优化配置。先将电力网络用图表示出来，再根据节点可观的PMU配置规则[4]，对形成的电网树进行如下描述[16]。

（1）若一个节点上配置PMU，则周边节点位置均可知，如图1所示。

图1 规则1图示Fig.1 The expression of rule 1

（2）若两节点位置已知，则其连通方式可知，如图2所示。

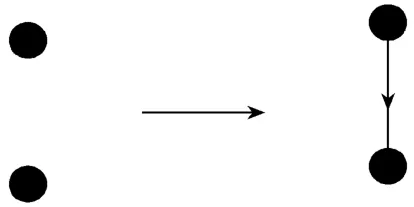
图2 规则2图示Fig.2 The expression of rule 2

（3）假设一个节点不与自身连通，仅与周边的N个节点连通，若该节点与其周边的N-1个节点的连通方式已知，则其与第N个节点的连通方式可知，进一步可知，该节点位置可知，如图3所示。

图3 规则3图示Fig.3 The expression of rule 3

（4）一个不与自身连通的节点周边与之相连的所有节点位置已知，则该节点的位置可知。进一步可知，该节点与周边所有节点的连通方式均可知，如图4所示。

图4 规则4图示Fig.4 The expression of rule 4

通过上述分析，可得一个PMU配置节点的最大树形成如图5所示。

图5 PMU配置节点的最大树Fig.5 The maximum tree of PMU placement node

由于一棵最大树上的节点与支路信息均可知，故无需对最大树上所有节点配置PMU，可有效减少PMU的配置量。

对于两棵相邻的最大树，根据规则2，可连通生成一棵新的最大树，如图6所示。

图6 最大树的连通与生成Fig.6 The connection of maximum tree

1.3.2 全网PMU配置顺序

对于现阶段已少量配置PMU的输电网络，首先在这些PMU配置节点处生成最大树，由1.3.1节分析可得，这些最大树所在电网区域性可观，故该最大树上所有节点均不必配置PMU，由此可简化电网拓扑结构，减少电网中的PMU配置。

在输电电网中，总存在一些系统运行方式变化时会对全网产生重要影响的关键节点，这些节点的电气量信息观测尤为重要。因此，对于阶段性PMU配置的电网，应优先保证这类关键节点的可观性，实现其PMU配置。在本文第1.2节中，引入节点的潮流熵来反映节点受系统扰动的影响情况，从而得到各节点的脆弱性指标，见式（2）。对于各不可观节点，按照其脆弱性指数大小，决定其PMU安装顺序，有利于保证阶段性PMU安装效益最大化。

1.3.3 N-1下的电网安全性检查和PMU加装

电网内各元件由于承载负荷等条件不同，其事故发生概率不尽相同。仅对电网中脆弱性较高（易于发生事故）的节点加装PMU，一方面有利于保障这类节点的事故下可观性，增强电网可靠性，另一方面也避免了PMU安装不必要冗余，减少安装成本。为此，在PMU配置实现完全可观之后，应对脆弱性节点进行N-1故障的安全配置检查和加装。节点脆弱性指标定义见第1.2节，节点脆弱性指标Va≥v的节点称为脆弱性节点，其中v为脆弱性指标阈值。

因此，在加装PMU之前，首先要进行N-1条件下的可观性校验，避免PMU的重复冗余安装。根据N-1条件下节点可观的配置条件，基于N-1条件的可观性判断如下：

（1）若节点i∈P0，根据条件①，无需加装PMU。

（2）若节点i∈P1，根据条件②，若⊆P0则满足N-1下可观。

（3）若节点i∈P2，根据条件③，若存在两节点m∈、n∈且有m∈P、n∈P，则满足N-1下00可观。

其中，P0表示装配了PMU的节点集；1P表示自身未装配PMU并仅有一条连通支路的节点集；P2表示自身未装配PMU并有两条以上连通支路的节点集。

对于不满足N-1下可观性的脆弱性节点，应按节点可观的三种情况，进行PMU的加装。

2 算法流程

算法流程实施步骤如下：

1）根据电网规划和硬件条件，按照第1.1节所述系统分区方法将整个电网分为几个合理的 区域。首先，根据电网分区要求，确定分区权重Tω、Cω和Sω，本文中采用层次分析法求得；其次，根据电网硬件设施和系统参数，确定区域权衡指标和S*（指标定义及计算式见附录）；最后，采用遗传算法根据式（1）确定系统分区结果。

2）各区域根据自身电力发展、地理条件和经济因素等确定阶段性PMU配置目标。

3）根据第1.2节所述节点脆弱性指标定义，对各区域内节点进行脆弱性排序，并找出排名靠前（Va≥v）的脆弱性节点。

4）进行分区阶段性PMU配置，现作以下几点说明：

（1）在图7描述的算法流程中，本文在PMU配置节点处建立的最大树如图5和图6所示。

图7 PMU配置程序流程Fig.7 The program flow of PMU configuration

（2）在对下一节点进行PMU配置时，应满足以下四点最大树配置规则：①一棵最大树上的所有节点均无需配置PMU；②在满足第①条规则的前提下，优先对脆弱性排名的节点进行PMU配置；③若区域内两个满足PMU配置条件的节点的脆弱性排名相同，优先配置连通支路多的节点；④若区域内两节点的脆弱性排名相同且连通支路数量相等，优先配置距离原PMU配置区域最近的节点。

（3）对实现完全可观的电网进行N-1下的PMU安全校验和配置时，安全性检查规则如1.3.3节所述。为合理利用正常运行状态下的PMU配置，现对PMU加装提出了以下三个要求：①若，要求在节点i加装PMU，使得i∈P0；②若对于任两节点均有m∉P0,n∉P0，要求在节点i加装PMU，使得i∈P0；③若对于有m∈P0，且对于任一有n∉P0，要求在与节点i连通的一条节点上加装PMU，即要求满足对于某一，使得k∈P0。

3 算例分析

3.1 算例结果

文中以IEEE 39节点系统为例对本文提出的方案进行测试，该系统总共包括10台发电机，12台变压器，39个节点，34条支路，其他系统参数设置见附录。

1）进行电网分区。在利用遗传算法对系统进行分区之前，要确定目标函数式（1）中的各项参数。文中假定通信质量和经济效益两个指标同等重要，且相对均衡性指标略重要。根据AHP法，确定目标函数为

根据式（3），采用遗传算法进行区域划分，其中算法的种群规模设为150，交叉率设为0.9，变异率设为0.01，终止条件为目标函数连续20代不变，得到分区结果如图8所示。

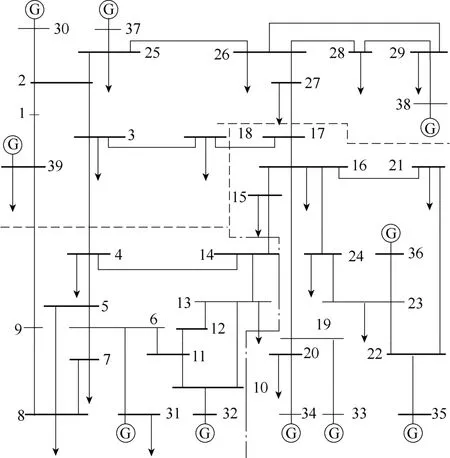
图8 IEEE 39节点系统分区Fig.8 The partition graph of IEEE 39 node system

2）统计全网已有PMU配置，确定各区域节点PMU阶段性配置规划。假设系统中节点5、27已安装PMU，根据阶段性规划，各区域每个阶段每个区域最多配置一个PMU。

3）对每个故障区域内的节点进行脆弱性评估，将脆弱度较大的节点排名列于表1。

4）采用图论的方法对系统进行不完全可观情况下的PMU分阶段配置和N-1情况下的PMU加装校验。

表1 节点脆弱性排序Tab.1 The node vulnerability ranking

在系统未达到完全可观阶段，根据节点脆弱性指标从高到低，采用最大树原理进行PMU的优化配置分阶段配置结果见表2。

表2 分阶段配置PMU结果Tab.2 The results of stage PMU

当配置达到系统完全可观后，对其进行N-1的脆弱性节点配置。本文将所有节点分为三类：重度脆弱节点（节点脆弱性指数Va≥0.5）、中度脆弱节点（节点脆弱性指数Va≥0.1）和强壮节点（节点脆弱性指数Va＜0.1）。优先选择对重度脆弱节点进行PMU配置校验和加装，在经济条件许可的基础上，可以进一步考虑对中度脆弱节点进行PMU加装。加装结果见表3。

表3 防范N-1故障的脆弱性节点加装Tab.3 The vulnerability node installation on guard of N-1 faults

3.2 几种配置方法分析比较

为了对本文所述方法进行更好的说明，下面将其与几种常用的配置方法进行比较，结果见表4。

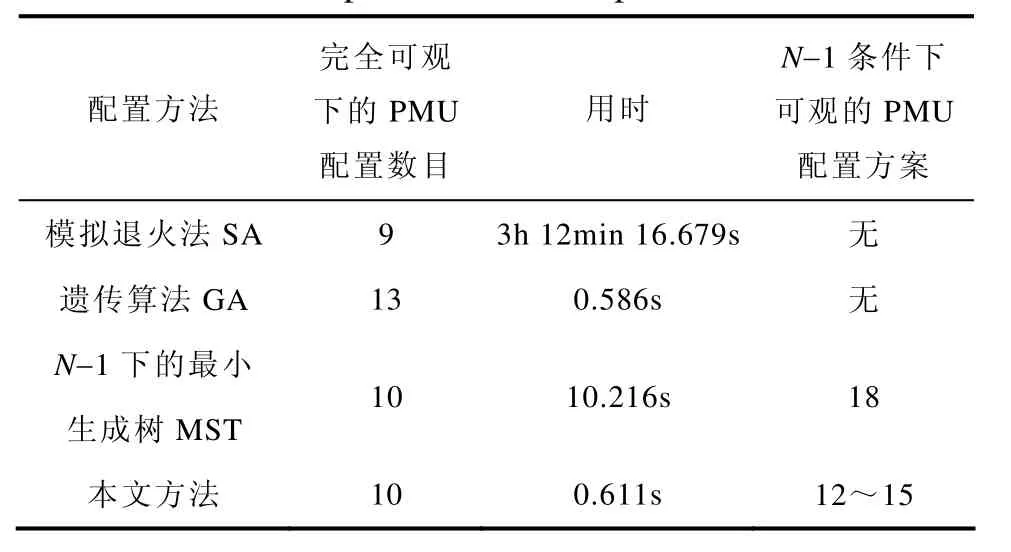
表4 几种PMU配置方法比较Tab.4 The comparison of PMU placement methods

将上述四种方法进行比较，可以发现：

（1）模拟退火法配置所需PMU虽然少，但是用时过长，并且没有考虑电网的实际需求，必须一次性完成全网的PMU配置方能达到良好的监测效果，然而一次性完成全网PMU配置所需花费过高，这在广域电网中是不切实际的。

（2）遗传算法用时最短，但完全可观下PMU配置所需数量也最多，这是由于遗传算法易收敛于局部极值点，且这两种方法在N-1情况下很有可能失去可观性。

（3）最小生成树法在N-1条件下仍能保证系统可观性但是所需PMU数目过多，相当于系统节点总数的46%。

（4）本文提出的PMU配置方案仅需12个PMU配置，即可基本保障系统在N-1条件下的可观性，即使发生严重的大电网事故，15个PMU的配置也足以使系统保持可观，可以认为是在经济性、安全性和时间效益方面均取得了良好的成效。此外，本文所述方法可实现PMU的分阶段配置，充分考虑到现有电网中已装配PMU的部分区域情况，这一点与传统的一次性考虑全网PMU配置的方法相比是极具优势的。

4 结论

本文提出了一种基于图论的分阶段PMU优化配置方案，该方案在考虑现有PMU配置和电网区域性发展水平的基础上，根据各节点对电网安全性的重要程度，依次进行PMU配置。该方案为PMU的分阶段优化配置提出了合理的建议，并且有效保证了电网事故时仍不失可观性，具有灵活性好、计算速度快和经济效益高的特点。

附 录

1. 系统分区指标说明

1）通信指标

根据WAMS的运作机理，由PMU测量所得的电气量信息往往需要传送到数据处理中心进行分析和处理，假设每个分区中仅设置一个数据处理中心，称之为通信主站，则主站Ok所在的分区中，通信延时的最大值决定了该区域内的通信质量，各分区延时的最大值又决定了整个系统的通信质量。定义全网分区最大的通信延时为Tmax，作为本文通信质量的评价标准

式中，M为通信主站Ok所在分区中的PMU总数；Q为电网分区总数，Q≪N，N为电网内PMU总数；Ok为第k个分区的主站，k=1,2,…,Q。

电力系统中任意两个PMU之间的通信延时可以表示为[12]

式中，T为任意两个PMU之间的通信延时；Ts为数据穿行发送延时，Ts=Ps/Dr，Ps为数据包长度，Dr为网络数据传输速率；Tb为数据包传输间隔延时，Tb很小，可忽略不计；Tp为通信通道延时，Tp=l/v，l为PMU之间通信通道的长度，v为通信通道传输数据的速率；Tr为路由排队延时，k为两PMU之间数据传输经过的路由器数，λ为数据包的平均到达速率，ξ 为路由器的服务速率。

除k、l外，其他变量均由通信系统硬件条件决定，对于一确定的电力系统可视为常数，故任意两PMU的通信延时仅与k、l相关，通信信道越长，经过的路由器越多，通信延时就越大。

2）经济指标

电力系统的投资费用、运行维护费用是电力系统研究时必须要考虑的因素，将这两种费用统称为设备费用，记为CΣ，作为本文经济效益衡量指标

式中，N为全网PMU总数；L为全网输电线路总数；CM为分区主站设备费用，与分区的数目（或者说主站的个数）Q成正比，包括数据集中器、存储单元和决策中心单元等设备；CS为各分区PMU配置费用；CC为广域保护通信网络设备费用，包括光纤通道和路由交换设备等。

3）均衡性指标

引入分区保护元件的标准方差，作为均衡性评估指标

式中，Mk为分区k中被保护元件的个数；Mav为各区域被保护元件数目的平均值。

2. 通信质量相关固定参数

附表 通信参数App.Tab. Communication parameters

3. 节点脆弱性指标计算

节点a在支路k上的潮流分布因子Dka定义为

式中，xcd为支路k的电抗；Xda、Xca为正常情况下电网的节点阻抗矩阵内的对应元素。

假设系统在正常工况下处于平衡基态，此时支路k的潮流为Pk0；当节点a受到单位负荷扰动时，即ΔPa=1，支路k的潮流为Pka，节点a受到扰动后引起的潮流增量为

将ΔEka定义为节点a对支路k的潮流冲击，则节点a对系统的冲击为

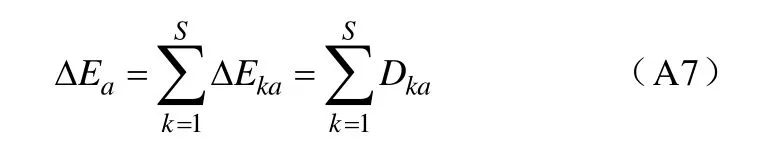
式中，S为系统支路数。

支路k承担的节点a对系统冲击的比例用支路k的潮流冲击率ηka=ΔEkaΔEa表示。则可定义节点a的潮流熵为

HD(a)的大小反映了不同节点受到扰动时系统所受到的潮流冲击的分布特性。当各支路均摊节点a的冲击能量时，各支路受到的冲击影响均不大，因此系统所承受的节点扰动较小；而当冲击全部集中在某一条或几条支路时，节点扰动会对系统产生很大的冲击，极易引起事故发生。

由此，定义节点的脆弱性指标为

参考文献

[1] 徐天奇, 尹项根, 游大海, 等. 广域保护系统功能与可行结构分析[J]. 电力系统保护与控制, 2009, 37(3): 93-97.

Xu Tianqi, Yin Xianggen, You Dahai, et al. Analysis on functionality and feasible structure of wide area protection system[J]. Power System Protection and Control, 2009, 37(3): 93-97.

[2] 杨春生, 周步祥, 林楠, 等. 广域保护研究现状及展望[J]. 电力系统保护与控制, 2010, 38(9): 147-150.

Yang Chunsheng, Zhou Buxiang, Lin Nan, et al. Research current status and prospect of wide-area protection[J]. Power System Protection and Control, 2010, 38(9): 147-150.

[3] Aminifar F, Lucas C, Khodaei A, et al. Optimal placement of phasor measurement units using immunity genetic algorithm[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1014-1020.

[4] 彭疆南, 孙元章, 王海风. 考虑系统完全可观测性的PMU最优配置方法[J]. 电力系统自动化, 2003, 27(4): 10-16.

Peng Jiangnan, Sun Yuanzhang, Wang Haifeng. An optimal PMU placement algorithm for full network observability[J]. Automation of Electric Power Systems, 2003, 27(4): 10-16.

[5] Hajian M, Ranjbar A M, Amraee T, et al. Optimal placement of PMUs to maintain network obser-vability using a modified BPSO algorithm[J]. International Journal of Electrical Power & Energy Systems, 2011, 33(1): 28-34.

[6] Nuqui R F, Phadke A G. Phasor measurement unit placement techniques for complete and incomplete observability[J]. IEEE Transactions on Power Delivery, 2005, 20(4): 2381-2388.

[7] 罗毅, 赵冬梅. 电力系统PMU最优配置数字规划算法[J]. 电力系统自动化, 2006, 30(9): 20-24.

Luo Yi, Zhao Dongmei. Optimal PMU placement in power system using numerical formulation[J]. Automation of Electric Power Systems, 2006, 30(9): 20-24.

[8] 张恺伦, 江全元. 基于攻击树模型的WAMS通信系统脆弱性评估[J]. 电力系统保护与控制, 2013, 41(7): 116-122.

Zhang Kailun, Jiang Quanyuan. Vulnerability assessment on WAMS communication system based on attack tree model[J]. Power System Protection and Control, 2013, 41(7): 116-122.

[9] 姜宪国, 王增平, 李琛, 等. 区域自治式后备保护分区方案[J]. 电工技术学报, 2013, 28(1): 234-241.

Jiang Xianguo, Wang Zengping, Li Chen, et al. Zoning scheme of regional autonomy backup protection[J]. Transactions of China Electrotechnical Society, 2013, 28(1): 234-241.

[10] 熊小萍, 谭建成, 林湘宁. 基于MPLS的广域保护通信系统路由算法[J]. 电工技术学报, 2013, 28(6): 257-263.

Xiong Xiaoping, Tan Jiancheng, Lin Xiangning. Routing algorithm for communication system in wide-area protection based on MPLS[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 257-263.

[11] Stahlhut J W, Browne T J, Heydt G T, et al. Latency viewed as a stochastic process and its impact on wide area power system control signals[J]. IEEE Transactions on Power Systems, 2008, 23(1): 84-91.

[12] 喻洁, 黄学良, 夏安邦. 基于分区协调优化的环境经济调度策略[J]. 电工技术学报, 2010, 25(1): 129-136.

Yu Jie, Huang Xueliang, Xia Anbang. Environmental economic dispatch based on sub-area coordinated optimization[J]. Transactions of China Electrotechnical Society, 2010, 25(1): 129-136.

[13] 潘静娟. 区域集中决策式广域后备保护研究[D].武汉: 华中科技大学, 2012.

[14] 李勇, 刘俊勇, 刘晓宇, 等. 基于潮流熵的电网连锁故障传播元件的脆弱性评估[J]. 电力系统自动化, 2012, 36(19): 11-16.

Li Yong, Liu Junyong, Liu Xiaoyu, et al. Vulnerability assessment in power grid cascading failures based on entropy of power flow[J]. Automation of Electric Power Systems, 2012, 36(19): 11-16.

[15] 陈东升, 李科学, 赵丽宾. Fuzzy图最大树聚类方法及其应用[J]. 运筹与管理, 2007, 16(3): 69-73.

Cheng Dongsheng, Li Kexue, Zhao Libin. Fuzzy graph maximal tree clustering method and its application[J]. Operations Research and Management Science, 2007, 16(3): 69-73.

[16] 彭春华. 基于免疫BPSO算法与拓扑可观性的PMU最优配置[J]. 电工技术学报, 2008, 23(6): 119-124.

Peng Chunhua. Optimal PMU placement based on immune BPSO algorithm and topology observability[J]. Transactions of China Electrotechnical Society, 2008, 23(6): 119-124.

徐 岩 男，1976年生，博士，副教授，研究方向为电力系统保护与控制、新能源发电和智能电网。

E-mail: xuyan@ncepubd.edu.cn（通信作者）

应璐曼 女，1990年生，硕士研究生，研究方向为电力系统保护与控制。

E-mail: ylm829@163.com

作者简介

收稿日期2014-01-09 改稿日期 2014-07-02

中图分类号：TM744