不平衡及谐波电网下基于静止坐标系的并网逆变器直接功率控制

沈永波 年 珩（浙江大学电气工程学院 杭州 310027）



不平衡及谐波电网下基于静止坐标系的并网逆变器直接功率控制

沈永波 年 珩
（浙江大学电气工程学院 杭州 310027）

摘要为提高电网不平衡及电网背景谐波下电压源并网逆变器的运行性能，以静止坐标系下并网逆变器数学模型为基础，提出不平衡及谐波电网下并网逆变器的直接功率控制策略，实现输出功率平稳或输出电流平衡且正弦的两个独立的控制目标。所提控制策略使用降阶广义积分器实现对电网电压基频分量的快速准确提取，从而计算得到输出电流平衡且正弦控制目标下的功率参考补偿项。所提控制策略使用矢量比例积分谐振器实现对功率参考中波动分量的精确控制。最后通过构建并网逆变器实验系统，对所提控制策略的可行性和有效性进行了实验验证。

关键词：电网不平衡 电网背景谐波 电压源并网逆变器 直接功率控制 降阶广义积分器矢量比例积分控制器

Stationary Frame Direct Power Control of Grid-Connected Inverter under Unbalanced and Harmonic Grid Voltage

Shen Yongbo Nian Heng
（College of Electric Engineering Zhejiang University Hangzhou 310027 China）

Abstract This paper proposes a direct control strategy for voltage source grid connected inverter (VSI), based on the mathematic model of VSI on the stationary frame, to enhance the operation performance of VSI under the unbalanced and harmonic grid voltage. This strategy can implement two alternative control targets, i.e., stable output active and reactive power, as well as balanced and sinusoidal output current. The reduced order generalized integrator (ROGI) is applied to quickly decompose the positive sequence component of the grid voltage, further to calculate the power reference compensations. Vector proportional integrator (VPI) is used to control the power ripple components accrately. Finally, the experiment system of VSI is built to validate the proposed DPC strategy.

Keywords：Unbalanced grid, harmonic grid, voltage source grid-connected inverter, direct power control, reduced order generalized integrator, vector proportional integrator

0 引言

近年来电压源并网逆变器（Voltage Source gridconnected Inverter, VSI）因其具有电流正弦度高、有功功率和无功功率独立调节等优势，被广泛用于智能电网、分布式发电及高压直流输电系统[1,2]。当电网电压含有不平衡及谐波分量时，传统控制策略下VSI将产生交流电流畸变且输出功率波动，进一步恶化了电网电压的不平衡度和增大了谐波含量，导致无法满足并网运行要求[3,4]。

在不平衡及谐波电网下的VSI控制策略研究中，已有文献通过在同步旋转坐标系中使用矢量控制（Vector Control, VC）[5,6]或直接功率控制（Direct Power Control, DPC）[7]实现电流正弦或输出功率平稳。由于需要通过坐标旋转变换[8,9]使逆变器电流各倍频及正负序分量转换成直流量进行控制，必须采用同步坐标系下锁相环（Synchronous Reference Frame Phase Lock Loop, SRF-PLL）跟踪电网电压的相位。需要指出的是，SRF-PLL是一个对输入电压的二阶开环传递函数，引入SRF-PLL必然会降低系统的动态响应能力[10]。

为了避免PLL对VSI在不平衡及谐波电网下动态响应的影响，基于静止坐标系的控制策略得到了广泛的研究与关注。在不平衡电网下，文献[11]基于VC策略采用比例谐振（Proportional Resonant, PR）调节器跟踪电流参考，实现VSI输出电流正弦。文献[12]将滑模控制与DPC结合，实现了不平衡电网下VSI有功、无功输出平稳或者电流正弦三个控制目标。需要指出的是，以上文献都没有考虑到电网电压中存在的谐波分量。

当考虑电网谐波分量时，以5、7次谐波为例，在静止坐标系下的VC中需要增加5、7倍频的谐振器以控制相应的谐波电流，而DPC只需要增加6倍频的谐振器用于控制功率波动。因此，不平衡及谐波电网下使用DPC增加的谐振器数量少，有利于简化系统的复杂性，更适用于VSI的高性能控制。此外，考虑到DPC不同控制目标下参考值计算较为简单，更适用于不平衡及谐波电网下VSI的高性能运行。但是，目前还没有相关文献研究不平衡及谐波电网电压下VSI在静止坐标系下的DPC策略。需要指出的是，DPC又分为基于开关表滞环控制（Hysteresis Controller, HC）和基于空间矢量调制（Space Vector Modulation, SVM）两种方式[12-14]，均具有良好的稳态和动态功率控制性能。其中SVM-DPC具有恒定开关频率的优势[14]，更易于滤波装置的设计。

因此本文提出了不平衡及谐波电网下基于静止坐标系VSI的SVM-DPC策略。通过建立静止坐标系下VSI的DPC数学模型，以实现不平衡及谐波电网下的两个独立运行目标：①有功功率和无功功率输出平稳；②三相电流输出平衡且为正弦波。为计算电流平衡且正弦目标下的功率参考补偿，引进了降阶广义积分器（Reduced Order Generalized Integrators, ROGI）提取电网电压各序分量，改进了其离散化实现方法。通过建立系统传递函数，分析了系统控制性能。最后通过构建实验系统对本文提出控制策略进行验证。

1 不平衡及谐波电网下VSI数学模型

图1为三相VSI电路，电流参考方向从电网流向逆变器。图中，uga、ugb和ugc为电网电压，vga、vgb和vgc为逆变器交流侧电压，iga、igb和igc为三相电流，L、R分别为进线电抗器电感和电阻。由图1可得VSI在αβ静止坐标系下的数学模型为[12]

式中，下标α、β表示在两相静止坐标系下α和β轴分量。

图1 并网逆变器电路Fig.1 Circuit scheme of grid connected VSI

在αβ两相静止坐标系下，VSI从电网吸收的瞬时功率可表示为[12]

式中，ugα、ugα和igα、igα为电网电压和电流在αβ两相静止坐标系下分量。

考虑到电网中5、7次谐波含量最大，危害也最大，本文只研究5、7次谐波电压下的控制策略，但研究的控制策略同样适用于电网其他谐波下的控制。因此，本文研究中不平衡及谐波电网电压主要包括基频正序分量、基频负序分量、5倍频负序分量和7倍频正序分量。此时，电网电压在两相静止坐标系下可表示为[3]

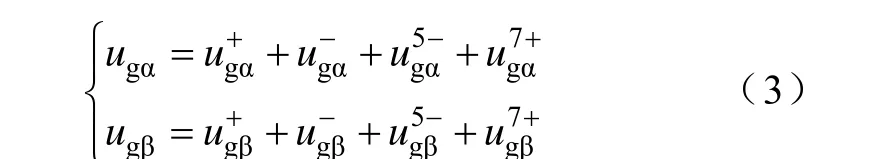
根据式（1）可知，两相静止坐标系下电流对时间的导数为

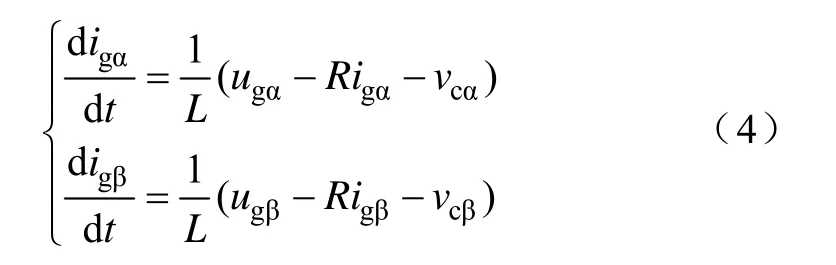
式中，vcα、vcβ是逆变器输出电压在两相静止αβ 坐标系下分量。

根据式（3），不平衡及谐波下电网电压对时间的导数可表示为

式中，ωg为电网基频角频率。

对式（2）求导，可得功率的导数为

式中，Pg、Qg是逆变器输出有功和无功功率。

将式（4）和式（5）代入式（6），可得不平衡及谐波电网下VSI的DPC控制方程为

式中，GC(s)是PI和VPI控制器的传递函数；Δugα、Δugβ是电压解耦补偿项；P*g、Q*g是逆变器输出有功和无功功率参考值。

式（7）中，为实现对功率信号的无静差调节，本文将比例积分（Proportional Integral, PI）控制器和矢量比例积分（Vector Proportional Integral, VPI）谐振控制器用于调节功率误差信号，因此式（7）中的电压参考计算可以重新表示为式（10）。虽然式（9）中功率补偿项存在电压微分运算，但根据式（5）可知，电压微分运算可以转换成各个电压分量和电网角频率的加法和乘法运算，而各个电压分量可由降阶广义积分器提取获得，因此也无需对电压直接进行微分，避免了微分运算对控制引入的干扰。由式（7）可知，本文推导的静止坐标系下的DPC中引入了电网电压矩阵M，如式（8）所示。矩阵M的作用是将调节器输出的功率信号转换成静止坐标系下的电压控制信号输入到SVPWM。而在同步旋转坐标系下DPC[7]，通常是利用PLL将调节器输出的电压控制信号经Park反变换后，变成静止坐标系下的电压控制信号输入到SVPWM。由此可见，本文控制结构中通过采用矩阵M，从而不需要PLL，避免了在电网电压畸变情况下PLL需要采用陷波器去精确锁定电网电压基频分量位置角度，因此本文所提的静止坐标系下DPC控制有利于简化控制结构。根据以上数学推导得到的控制方程，下文给出了本文所提DPC控制策略框图，用于实现特定控制目标，改善VSI在不平衡及谐波电网下的运行性能。

2 不平衡及谐波电网下的DPC策略

图2 不平衡及谐波电网下直接功率控制框图Fig.2 Direct power control scheme under unbalanced and harmonic grid conditions

根据式（7），图2给出了不平衡及谐波电网下VSI的DPC控制框图。图中，对电网电压和电流采样后经过静止坐标系Clarke变换得到ugα、ugβ和igα、igβ；通过式（3）计算得到VSI瞬时功率Pg、Qg；用ROGI提取电网电压的基波正序分量和用于计算功率参考补偿项Pgcom、Qgcom；Pgref、Qgref为VSI功率参考给定指令，一般为直流量；图中功率误差信号使用PI和VPI调节器分别进行控制，其中PI调节器用于控制功率误差直流分量，而VPI调节器用于抑制功率误差的倍频波动，这是一种基于零极点相消原理的谐振器，相比传统的PR控制器具有更好的稳定性[15]，具体分析见下文。

文献[3]分析指出，不平衡及谐波电网下VSI会产生5次、7次等谐波电流，而功率波动主要表现在二倍频和六倍频波动，其中二倍频功率波动是由电压基波负序分量和电流基波正序分量引起的，而六倍频功率波动是由电压5、7次谐波分量和电流基波正序分量引起的。因此，控制需要采用二倍频和六倍频VPI谐振器用于追踪功率误差信号。

根据以上关于电流和功率恶化的分析，本文选择两个独立控制目标：①VSI输出有功和无功功率平稳；②VSI输出电流平衡且正弦；用于改善VSI在不平衡及谐波电网电压下的运行性能。必须指出，当电网包括不平衡和谐波电压时，逆变器输出有功平稳或无功平稳会导致输出电流存在谐波分量，所以本文选择了有功和无功同时平稳作为控制目标。为了实现以上两个不同控制目标，需要推导在不平衡及谐波电网电压下VSI直接功率控制的参考补偿项Pgcom、Qgcom，具体如下。

1）有功和无功功率平稳

为了使VSI输出有功功率和无功功率同时保持平稳，抑制有功和无功功率的二倍频和六倍频波动，使输出功率Pg、Qg等于给定功率Pgref、Qgref。因此不需要作功率参考补偿，功率参考补偿项为

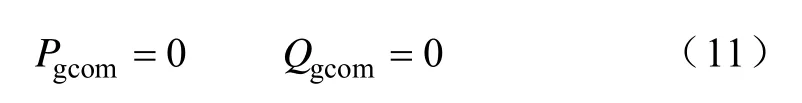
2）输出电流平衡且正弦

VSI瞬时功率表达式（2）可以重写为

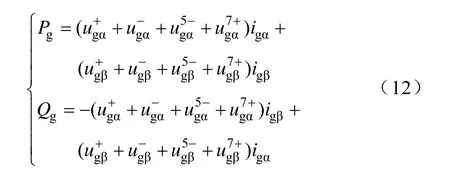
功率给定Pgref、Qgref是用于控制输出功率的直流分量，由于此目标下VSI输出电流只包括基波正序分量，即因此可认为

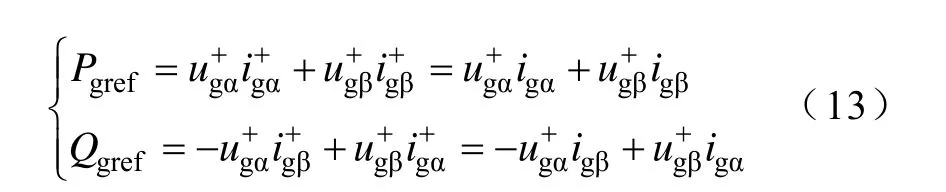
比较式（12）和式（13）可知，在理想电网电压下，两式应该相等；而在不平衡及谐波电网电压下，不平衡和谐波电压分量引起了两式之间的差值，因此，为了补偿电压基频负序、谐波分量和电流作用产生的功率波动，功率参考补偿项可表示为

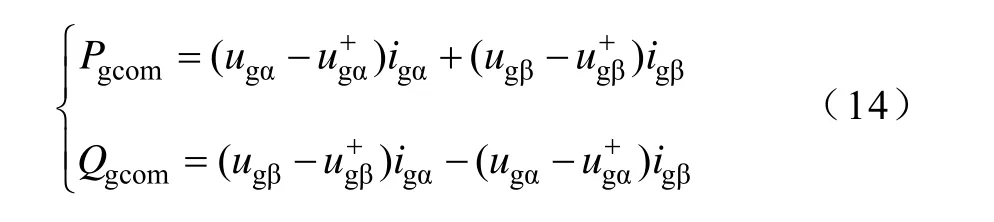
3 电网电压倍频正负序分量提取

当VSI控制目标为输出电流平衡且正弦时，需要分离出电网电压的基波正序分量ug+α、ug+β用于计算功率补偿（见式（14））。对于不平衡电网电压，常用的分离方法包括T/4延时法和滤波器法。由于T/4延时法的分离结果存在1/4周期的时延，致使当电网电压不平衡变化时的1/4周期内计算结果存在较大误差[16]。而当电网电压还存在谐波分量时，对电网电压延时后运算并不能瞬时消除-5、+7等谐波，因此不能有效提取出基波分量。本文采用基于ROGI的基波正序分量提取方法，这是一种可用于分离倍频及正负序分量的滤波器。相比于其他滤波器分离方法，ROGI方法的准确性高、速度快，尤其适用于弱电网及故障电网下对电网电压或者电流的分离提取[17,18]。

ROGI的连续域传递函数为

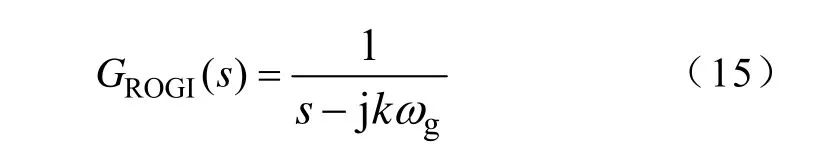
式中，kωg代表k倍基波角频率，k可以为正数或者负数，正、负号用于区分相同倍频的正序和负序分量。

实际中需要将ROGI在数字芯片中实现，因此必须将ROGI的传递函数表现为离散域形式。将z= esT代入式（15），可得到ROGI的离散域表达式为

ROGI只在谐振频率点附近具有较大的增益，并且会区分同一频率的正负序分量，因此适合于分离特定频率下的正负序分量。根据式（16），利用αβ坐标系下αβ分量的关系实现复系数运算，可得到ROGI滤波器的差分方程式为式中，T为采样周期。式（17）只需要4个状态输入量用于计算出2个输出量，较好地减少了计算量，在确保分离准确度和速度基础上更易于数字化实现。

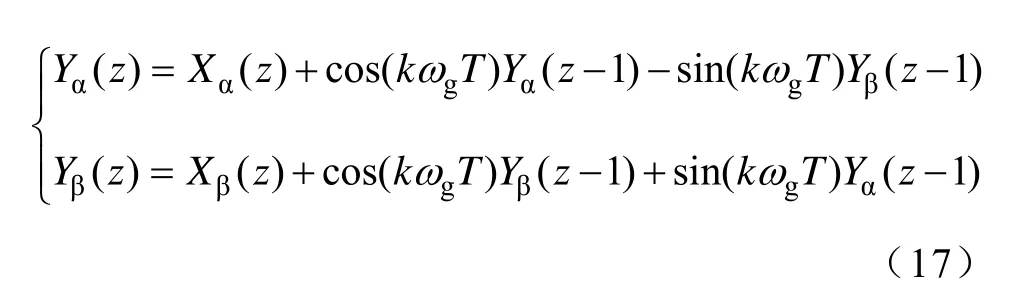
当电网电压同时存在负序分量和5次、7次谐波分量时，只需加入对应谐振频率的ROGI作电网电压各倍频正负序分量分离[17,18]。根据控制框图2可知，需要分离出电压基波正序分量用于计算功率参考补偿项，同时需要分离出用于计算电压解耦补偿项，因此图3中加入了基频正序负序分量、5次负序分量和7次正序分量对应的ROGI，从而可以提取出电网电压的各倍频正负序分量。图中，KROGI为增益系数，决定了ROGI法分离电网电压各倍频、正负序分量的速度。各倍频、正负序分量分离后要反馈到输入端，通过各倍频ROGI跟踪该误差信号，实现对各倍频、正负序分量的分离。

图3 降阶广义积分器分离法框图Fig.3 ROGI separation scheme

4 系统控制性能分析

根据图2可得功率控制环框图如图4a所示。图中EP和EQ为功率补偿项，可参考式（9）；左乘矩阵M（见式（8））；而左乘逆矩阵M-1可以参考瞬时功率计算表达式（2）。图4a中的GC(s)为控制器传递函数，Gplant(s)是逆变器主电路传递函数[19]，其表达式为

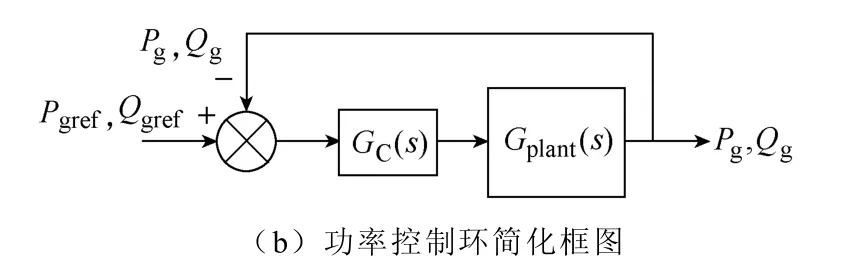
图4 功率控制系统框图Fig.4 Power control system diagram

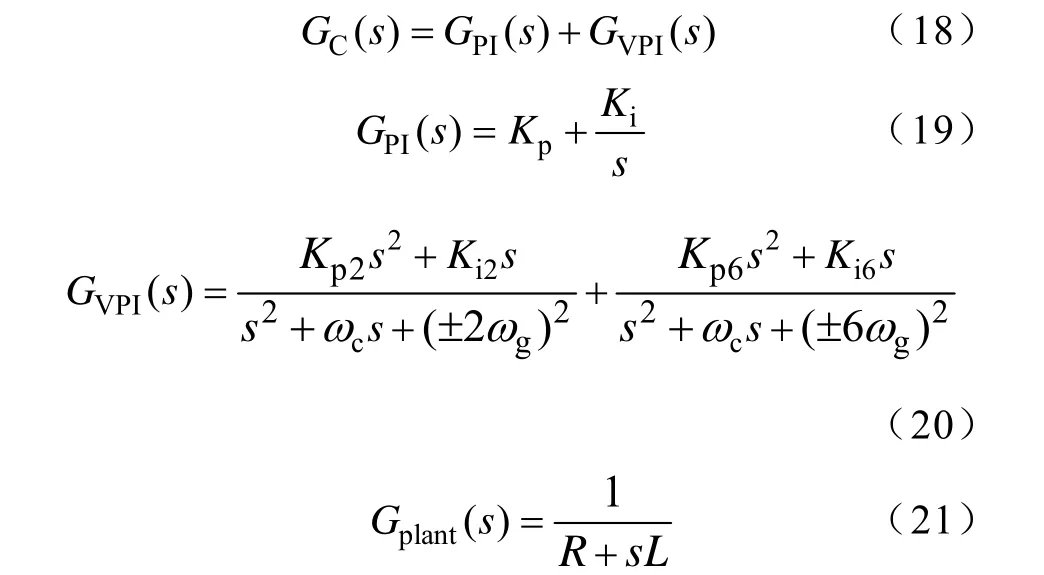
式中，Kp和Ki是PI控制器的控制参数；Kp2和Ki2是二倍频VPI控制器的控制参数，且而Kp6和Ki6是六倍频VPI控制器的控制参数，Ki6=(R/L)Kp6[18]；ωc是VPI控制的带宽；R和L是逆变器电路的进线电阻和电感。

为方便分析可将图4a中M矩阵和M-1逆矩阵相互抵消后，化简成如图4b所示框图。本文采用了VPI控制器实现对二倍频和六倍频功率误差信号的抑制，为了验证VPI控制器在DPC中的有效性，以六倍频VPI控制器为例进行开环传递函数分析，并与普通谐振器进行对比。

六倍频下采用普通谐振器得到的开环传递函数

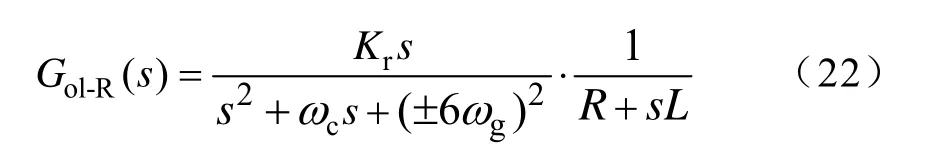
采用VPI控制器得到的开环传递函数为

取R=0.5Ω，L=5mH，Kr=2 000，Kp6=1，Ki6= (R/L)Kp6=100，ωc=5rad/s，ωg=100πrad/s。得到如图5所示的开环传递函数伯德图。

图5中普通谐振控制器和VPI控制器在谐振频率300Hz的幅值增益分别为32.5dB和32dB，表明两者在谐振频率点均具有较强的调节能力。但两个调节器在谐振频率点处表现出不同的相位响应。在谐振频率300Hz处普通谐振器的开环传递函数的相位为-87°。在频率大于300Hz以后的频率点上，相位接近-180°。因此，闭环系统的相位裕度较小，系统容易不稳定。而采取VPI控制器的开环传递函数在谐振频率点处的相位响应为0°，在谐振频率附近处最大相位响应在-90°左右，闭环控制响应具有接近90°的相位裕度。由此可见，采用VPI控制器比采用普通谐振器更有利于VSI系统的稳定。

图5 开环传递函数伯德图Fig.5 Bode diagrams of open loop transfer function

根据图4b可得VSI系统闭环传递函数为

将式（18）～式（21）代入式（24），同时设定R=0.5Ω，L=5mH，Kp=1，Ki=15，Kp2=1，Ki2=(R/L)Kp6= 100，Kp6=1，Ki6=(R/L)Kp6=100，ωc=5rad/s，ωg= 100πrad/s。图6给出了VPI控制器功率闭环传递函数的幅频和相频特性。从图6中可知，PI调节器确保了系统对直流量的控制具有0dB的幅值增益和0°的相位增益；而二倍频和六倍频VPI控制器确保了闭环系统在谐振频率100Hz和300Hz处具有0dB的幅值增益和0°的相位增益。因此，采用PI控制器和VPI控制器的控制结构可以保证在不平衡及谐波电网下给定功率信号和实际功率信号幅值和相位一致。

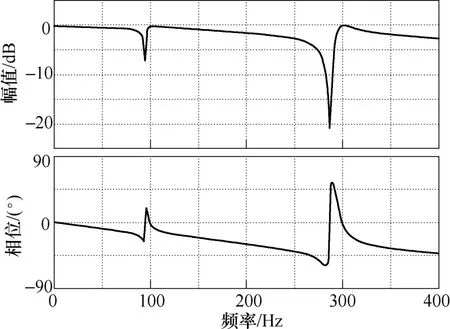
图6 闭环系统伯德图Fig.6 Bode diagrams of close loop transfer function

5 实验结果

为了验证所提控制策略不平衡及谐波电网下VSI的DPC策略可行性和有效性，构建了VSI实验平台，实验平台框图如图7所示。直流侧电压由直流稳压电源提供，交流侧通过变压器接到三相电网，三相不平衡及谐波电网由可编程电源Chroma 61704产生，并网逆变器采样频率和开关频率均设定为10kHz，系统控制采用DSP TMS320F2812芯片实现，实验波形通过横河DL750录波仪采集。表1给出了实验系统参数。

图7 实验平台系统框图Fig.7 Schematic diagram of the experiment system

表1 实验系统参数Tab.1 System parameters of experiment

为了分析不平衡及谐波电网下ROGI对电网电压基波正序分量的提取能力，图8给出了电网电压中突加谐波后，T/4延时法在前1/4周期内的电压基频正序波形，由图8可见波形是畸变的，而ROGI法则基本保持正弦。由此可见，ROGI法相比于T/4延时法具有更好的动态响应能力。再者，谐波倍频的ROGI可以提取电网电压其他谐波分量，而延时提取方法并不能实现对谐波分量的有效提取。因此，本文所提控制系统中采用ROGI分离法更适合逆变器在不平衡及谐波电网下运行。

图8 电网电压基频正序分量分离实验结果Fig.8 Experiment results of grid voltage fundamental positive sequence separation

基于构建的实验系统，对不平衡及谐波电网下并网逆变器两个独立控制目标下的稳态和动态性能进行了实验验证。图9给出了理想电网（电压包含负序分量0.7%、5次谐波0.11%和7次谐波0.07%）下并网逆变器在传统DPC策略（即图2中无功功率补偿计算和VPI环节）的实验结果，作为不平衡及谐波电网电压下本文所提DPC控制策略对照实验波形。

图9 理想电网下传统DPC控制策略实验结果Fig.9 Experimental results under ideal grid conditions with traditional DPC strategy

图9中VSI输出的有功功率给定Pgref从400W阶跃至1 000W，无功功率给定Qgref保持为0。由图9可知，系统输出有功功率Pg可在10ms内达到给定值，且无明显超调。当VSI输出有功功率Pg=1 000W时的稳态运行数据见表2，VSI三相输出电流THD为2.22%，有功功率波动±18W，无功功率波动±16var。由此可见，理想电网下VSI的直接功率控制具有较好的动态响应能力，但其稳态运行时电流谐波和功率波动仍然存在。

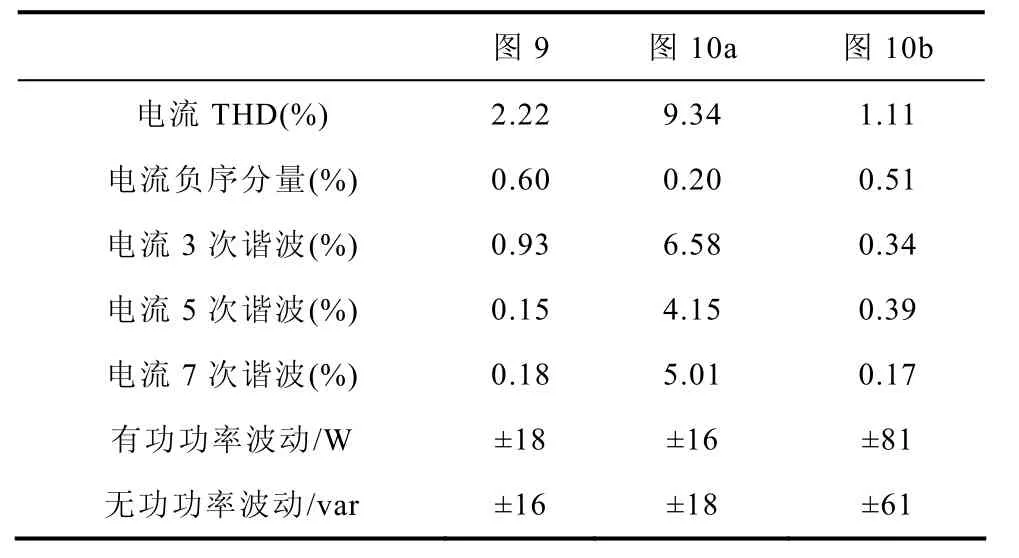
表2 实验数据分析Tab.2 Analysis of experiment data

为验证本文针对不平衡及谐波电网所提静止坐标系下DPC策略（见图2）的有效性和正确性，构造了包含负序分量6.13%、5次谐波分量5.97%和7次谐波分量3.43%的电网电压条件，得到实验波形如图10所示。图10a为本文所提DPC策略下VSI输出有功和无功功率平稳目标下的实验波形，图10b为VSI输出电流正弦且对称目标下的实验波形，图10c为以上两个目标切换瞬间的实验波形。

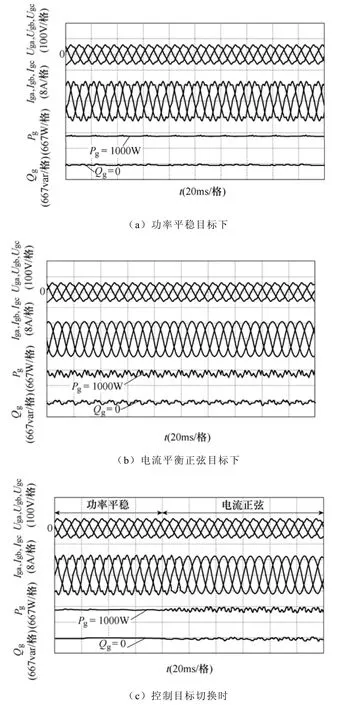
图10 VSI实验结果Fig.10 Experimental results of VSI

图10a的实验数据见表2，VSI输出有功功率波动±16W，无功功率波动±18var。由此可见，与图9相比，本文改进后的DPC控制策略实现了瞬时输出功率平稳的目标，功率波动与在理想电网运行的水平相当。该实验结果验证了本文采用的二倍频和六倍频VPI控制器在谐振点上具有较好增益，抑制了二倍频和六倍频功率波动。但此目标下的电流畸变严重，THD为9.34%，其结果与文献[3]中的数学推导一致。

图10b的实验数据见表2，VSI输出电流THD 为1.11%，其中包含负序分量0.51%、5次谐波0.39% 和7次谐波0.17%，与图9传统DPC在理想电网运行的情况电流THD相当。由此可见，本文第1节用于使VSI输出电流正弦且平衡控制目标的功率参考补偿项是正确的，该项省去了对VSI输出电流的分离提取，有利于系统控制结构简化，减少控制系统的计算时间。

但在此目标下，瞬时功率出现了二倍频和六倍频叠加得到的波动。这与文献[3]中数学模型推导一致，电流平衡且正弦必然会导致瞬时功率出现二倍频和六倍频波动。实验结果中，瞬时输出功率Pg、Qg的二倍频和六倍频波动分量叠加后总的功率波动波形如图10b所示。需要指出的是，二倍频和六倍频有功和无功功率波动分量受到电网电压各倍频分量相位和电流相位的影响，两者叠加后得到的瞬时有功和无功功率波动规律也会随之改变。因此，有功功率波动和无功功率波动并不是一致的。

图10c为在VSI稳态运行中切换控制目标瞬间的实验波形。从图10c可知，在稳态运行过程中，控制目标切换之后存在20ms的过渡过程，但较快稳定，不会引起系统振荡。由此可见，本文提出的DPC控制策略可实现两个控制目标之间的平滑切换。

图11 电流平衡正弦目标下功率变化时VSI实验结果Fig.11 Experimental results under target of balanced and sinusoidal output current with power change

图11给出了当VSI输出有功功率参考给定指令Pgref阶跃时的电流平衡且正弦目标下实验波形。图中VSI输出有功功率给定Pgref从400W阶跃到1 000W，对应的VSI输出有功功率Pg可在10ms实现功率跟随并保持稳定运行。图中虽然无功功率Qg出现了接近100var的超调，该超调量与图9是一致的，在50ms后基本稳定到给定值。出现超调的原因是无功与有功功率控制之间存在式（7）～式（10）所示的耦合关系，但是无功功率的变化确保了电流幅值基本保持恒定，实现输出电流的无超调运行。

图12给出了模拟实际电网谐波含量急剧恶化情况下本文控制策略在电流平衡且正弦目标下的实验波形。图中t0时刻突然加大谐波程度，t0时刻前后电网电压谐波程度已在图中标注，不平衡度都为6.13%。图中t0时刻以后20ms内的VSI输出电流波形存在较为明显的畸变，20ms后电流重新恢复到正弦。实验数据分析表明，t0时刻以前的VSI输出电流THD为1.01%，其中包含负序分量0.5%、5次谐波0.14%和7次谐波0.21%；t0时刻以后的VSI输出电流THD为1.14%，其中包含负序分量0.5%、5次谐波0.47%和7次谐波0.2%。该实验结果表明，当电网谐波含量发生变化时，本文提出的DPC控制策略可确保控制目标的准确实现，VSI在所提控制策略下具有较广范围电网电压谐波及不平衡度的适应能力，验证了所提控制策略的有效性和实用性。

图12 电流平衡正弦目标下谐波含量变化时VSI实验结果Fig.12 Experimental results under target of balanced and sinusoidal output current during the change of harmonic voltage percentage

6 结论

本文针对不平衡及谐波电网电压下运行的并网逆变器，提出了基于静止坐标系下DPC策略，实现了VSI输出电流正弦或功率平稳的控制目标。所提DPC策略中采用ROGI提取电网电压基波正序分量，避免了T/4延时法响应时间较慢和无法准确分离谐波的缺点，有效提高了动态响应能力。通过建立系统传递函数，分析了系统控制性能，证明所用控制器具有较好的稳定性。通过对不平衡及谐波电网电压下VSI的实验结果分析，验证了本文所提DPC策略具有优良的动、静态运行性能。

参考文献

[1] Carrasco J M, Franquelo L G, Bialasiewicz J T, et al. Power-electronic systems for the grid integration of renewable energy sources: a survey[J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1002-1016.

[2] Etxeberria-Otadui I, Viscarret U, Caballero M, et al. New optimized PWM VSC control structures and strategies under unbalanced voltage transients[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2902-2914.

[3] Hu J, Xu H, He Y. Coordinated control of DFIG's RSC and GSC under generalized unbalanced and distorted grid voltage conditions[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7): 2808-2819.

[4] Wang F, Duarte J L, Hendrix M A M, et al. Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 786-797.

[5] 章玮, 王宏胜, 任远, 等. 不对称电网电压条件下三相并网型逆变器的控制[J]. 电工技术学报, 2010, 25(12): 103-110.

Zhang Wei, Wang Hongsheng, Ren Yuan, et al. Investigation on control of three-phase grid-connected invertersunder unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2010, 25(12): 103-110.

[6] Quan Y, Nian H, Hu J, et al. Improved control of the grid-connected converter under the harmonically distorted grid voltage conditions[C]//IEEE International Conference on Electrical Machines and Systems (ICEMS), 2010: 204-209.

[7] Zhou P, He Y, Sun D. Improved direct power control of a DFIG-based wind turbine during network unbalance[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2465-2474.

[8] 刘波, 杨旭, 孔繁麟, 等. 三相光伏并网逆变器控制策略[J]. 电工技术学报, 2012, 27(8): 64-70.

Liu Bo, Yang Xu, Kong Fanlin, et al. Control strategy study for three phase photovoltaic grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 64-70.

[9] 吴云亚, 阚加荣, 谢少军. 基于双dq坐标系的并网逆变器控制策略[J]. 电工技术学报, 2011, 26(8): 106-112.

Wu Yunya, Kan Jiarong, Xie Shaojun. Control strategy for grid-connected inverter based on double dq coordinates[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 106-112.

[10] Golestan S, Monfared M, Freijedo F D. Designoriented study of advanced synchronous reference frame phase-locked loops[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 765-778.

[11] Wang F, Duarte J L, Hendrix M A M. Pliant active and reactive power control for grid-interactive converters under unbalanced voltage dips[J]. IEEE Transactions on Power Electronics, 2011, 26(5): 1511-1521.

[12] Shang L, Sun D, Hu J. Sliding-mode-based direct power control of grid-connected voltage-sourced inverters under unbalanced network conditions[J]. IET Power Electronics, 2011, 4(5): 570-579.

[13] Eloy-Garcia J, Arnaltes S, Rodriguez-Amenedo J L. Direct power control of voltage source inverters with unbalanced grid voltages[J]. IET Power Electronics, 2008, 1(3): 395-407.

[14] Zhi D, Xu L, Williams B W. Improved direct power control of grid-connected DC/AC converters[J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1280-1292.

[15] Yepes A G, Freijedo F D, Doval-Gandoy J, et al. Effects of discretization methods on the performance of resonant controllers[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1692-1712.

[16] Svensson J, Bongiorno M, Sannino A. Practical implementation of delayed signal cancellation method for phase-sequence separation[J]. IEEE Transactions on Power Delivery, 2007, 22(1): 18-26.

[17] Guo X, Wu W, Chen Z. Multiple-complex coefficient-

filter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1194-1204.

[18] 赵新, 金新民, 周飞, 等. 采用降阶谐振调节器的并网逆变器锁频环技术[J]. 中国电机工程学报, 2013, 33(15): 38-44.

Zhao Xin, Jin Xinmin, Zhou Fei, et al. A frequencylocked loop technology of grid-connected inverters based on the reduced order resonant controller[J]. Proceedings of the CSEE, 2013, 33(15): 38-44.

[19] Hwang J G, Lehn P W, Winkelnkemper M. A generalized class of stationary frame-current controllers for grid-connected AC-DC converters[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2742-2751.

[20] Lascu C, Asiminoaei L, Boldea I, et al. Frequency response analysis of current controllers for selective harmonic compensation in active power filters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(2): 337-347.

沈永波 男，1990年生，硕士研究生，研究方向为分布式发电系统及其控制。

E-mail: sampoly@zju.edu.cn

年 珩 男，1978年生，博士，教授，研究方向为分布式发电系统及其控制、风力发电系统及其控制等。

E-mail: nianheng@zju.edu.cn（通信作者）

作者简介

中图分类号：TM464

收稿日期2014-04-14 改稿日期 2014-11-26