变频器供电下定子磁动势引起的永磁同步电机转子损耗分析

沈启平韩雪岩（. 输变电装备及系统安全与新技术国家重点实验室（重庆大学） 重庆 400044 . 沈阳工业大学国家稀土永磁电机工程技术研究中心 沈阳 0870）



变频器供电下定子磁动势引起的永磁同步电机转子损耗分析

沈启平1韩雪岩2
（1. 输变电装备及系统安全与新技术国家重点实验室（重庆大学） 重庆 400044 2. 沈阳工业大学国家稀土永磁电机工程技术研究中心 沈阳 110870）

摘要随着分数槽集中绕组和高速高密度永磁同步电机的广泛采用，转子损耗受到越来越多的关注。在众多影响因素中，对其影响最大的当属定子磁动势谐波。在深入分析非正弦供电下电枢绕组磁动势的基础上，基于Steinmetz铁耗分离模型并考虑各次谐波路径不同提出一种转子损耗影响因子，该影响因子越大，电机的转子损耗就越大，反之亦然。采用所提出的转子损耗影响因子对8极9槽和8极48槽两种典型结构的转子损耗进行了分析，并通过有限元对两种结构的转子损耗进行了数值计算，说明了所提出的分析方法的有效性。

关键词：转子损耗 谐波损耗 损耗因子 透入深度 磁动势 永磁同步电机

教育部博士点基金（20130191120009），中央高校基本科研业务费（CDJZR13150009、CDJZR12205503），重庆市基础与前沿研究计划（cstc2013jcyjA0876）和输变电装备及系统安全与新技术国家重点实验室培育基金（2007DA10512713304）资助项目。

Rotor Loss Analysis of the Permanent Magnet Synchronous Machine Caused by Stator Magnetomotive Force with Converter Powering

Shen Qiping1Han Xueyan2
（1. State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400044 China
2. National Engineering Research Center for Rare Earth Permanent Magnet Machine Shenyang University of Technology Shenyang 110870 China）

Abstract As the wide applications of fractional-slot concentrated winding machine and high speed high power density permanent magnet synchronous machine (PMSM), the rotor loss has obtained more and more attentions. The impact of the stator magnetomotive force (MMF) harmonics is the biggest among many influence factors. After analyzing the stator MMF when it supplied by converter, a novel rotor loss influence factor ξk,vis proposed based on the Steinmetz separated iron loss model considering different magnetic paths of different harmonics. The bigger ξk,v, the more rotor loss is, and vice versa. Using the proposed rotor loss influence factor ξk,v, the rotor losses of two typical pole-slot combination machines with 8-pole 9-slot and 8-pole 48-slot respectively are analyzed. The finite element method (FEM) is then adopted to calculate the rotor losses of the two structures, and verifies the proposed analysis method.

Keywords：Rotor loss, harmonic loss, loss factors, skin depth, magnetomotive force, permanent magnet synchronous machine

0 引言

随着分数槽集中绕组和高速高密度电驱动技术的广泛应用，永磁同步电机的转子损耗受到大家的密切关注[1-3]，在某些领域转子损耗的存在已经使研究最热点由定子绕组转向转子，严重影响电机的安全可靠运行[4,5]。产生转子损耗的主要因素包括定子铁心开槽所引起的气隙磁导谐波，定子绕组基波电流所产生的气隙空间谐波磁动势和非正弦供电时定子绕组时间谐波电流所产生的气隙谐波磁动势，其影响最大的为绕组电流所产生的磁动势谐波[2,6,7]。

考虑到转子损耗影响的严重性，各国学者都对其展开了较为深入的研究，发表了大量文献[8-14]。文献[8]在对电机气隙磁场进行解析分析和一系列简化假设的基础上推导了表面式结构转子损耗的解析表达式，但结果十分复杂，不便于作为电机设计初始阶段的优选方案。鉴于此，文献[9]提出了一种较为快速的转子损耗计算方法，但其过程较为复杂，不够清晰。考虑到定子开槽所引起的气隙磁导谐波所产生的转子损耗较小[2]，文献[10,11]主要对分数槽集中绕组的表面式永磁同步电机定子磁动势所产生的转子损耗进行研究，但分析仅考虑了基波电流的影响，没有考虑时间谐波电流的影响。文献[2]在电流谐波的基础上对分数槽绕组定子磁动势所产生的转子铁心损耗进行了研究，结果表明分数次谐波是产生转子损耗的主要因素，且在转子外加导电护套并不能有效抑制转子损耗。

考虑到解析计算的复杂性和假设简化条件过多，有限元方法在转子损耗的计算方面得到了广泛的应用[15-19]。文献[16]对一台4极60槽400kW的永磁同步电机在直接转矩控制下空载和负载时的转子损耗进行了有限元分析，结果表明相同转速下空载时的转子损耗大于额定负载时的转子损耗。文献[17,18]对内置式整数槽永磁同步电机的转子损耗进行了有限元分析，结果表明定子齿槽谐波对转子损耗的影响大于时间谐波磁场对转子损耗的影响。但由于有限元法所需要的分析时间太长，且不便于分析不同因素对转子损耗的影响，所以其更加适合于电机设计的后期优化。

可以看出，目前关于永磁同步电机转子损耗的分析方法都不太适于电机设计初期的方案对比优选，所以本文在现有文献基础上，深入分析非正弦供电下定子磁动势对转子涡流损耗的影响，提出一种用于表征定子磁动势对转子损耗影响大小的转子损耗影响因子，从而指导电机设计的前期优选方案，最后采用有限元方法对所提出的理论进行验证。

1 定子磁动势分析

取A相绕组的轴线为空间角度θ的坐标原点，并选择A相电流达到最大值的瞬间作为时间的零点，不考虑不同次数谐波电流初相位的影响，三相绕组电流可表示为

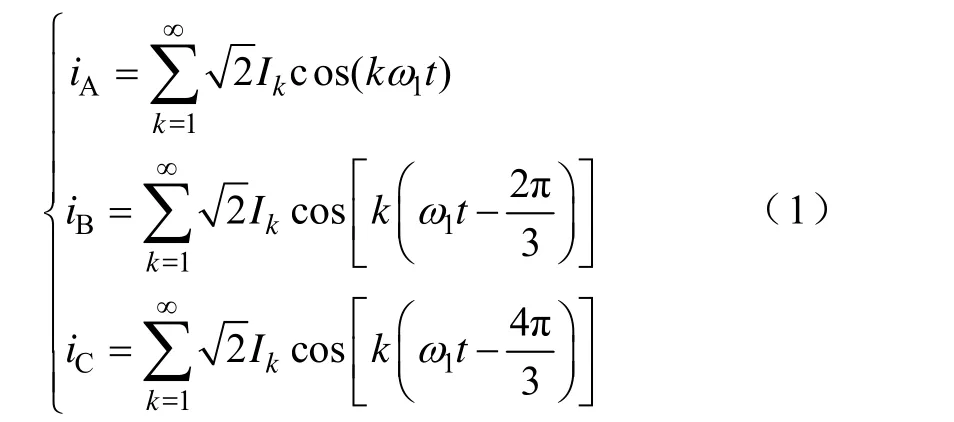
式中，k为时间谐波次数；Ik为k次时间谐波所对应的电流有效值；1ω为基波电流的电角频率。

那么A、B、C三相绕组中的k次时间谐波电流所产生的v次空间脉振磁动势可表示为式中，Fφk, v为k次时间谐波电流所产生的v次空间谐波脉振磁动势幅值，可表示为

式中，kw,v为v次空间谐波的绕组系数；N为相绕组串联匝数。

对式（2）展开后求和可得k次时间谐波电流所产生的v次空间谐波合成磁动势为

从式（4）可以看出，k次时间谐波电流所产生的v次空间谐波合成磁动势中包含正转和反转两种磁动势，下面对不同次数的合成磁动势分别讨论。

满足该条件的时间谐波次数k和空间谐波次数v可表示为

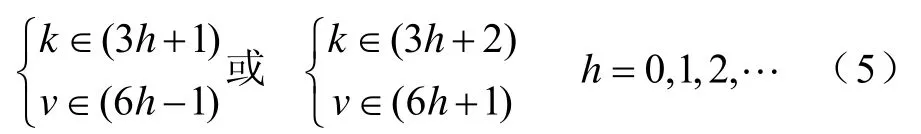
例如：基波电流（k=1）所产生的空间谐波磁动势v=5,11,17,··和5次谐波电流（k=5）所产生的空间谐波磁动势v=1,7,13,··等谐波组合均属于该类特点。该类合成磁动势为旋转磁动势，其幅值Fk, v和相对定子的频率ωk, v分别为

式（7）中，负号表示其旋转方向与基波转向相反，相对于转子的频率为

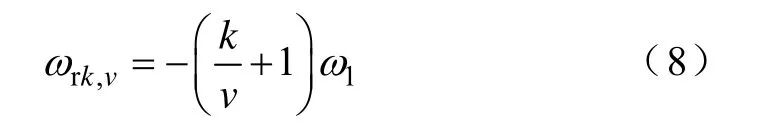
满足该条件的时间谐波次数k和空间谐波次数v可表示为

例如：基波电流所产生的空间谐波磁动势v=1,7,13, ··和5次谐波电流所产生的空间谐波磁动势v=5,11,17,··等谐波组合均属于该类特点。该类合成磁动势为一旋转磁动势，其幅值Fk, v和相对于定子的频率ωk, v分别为相对于转子的频率为

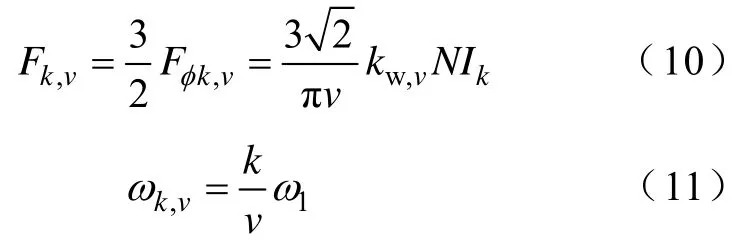
满足该条件的时间谐波次数k和空间谐波次数v可表示为

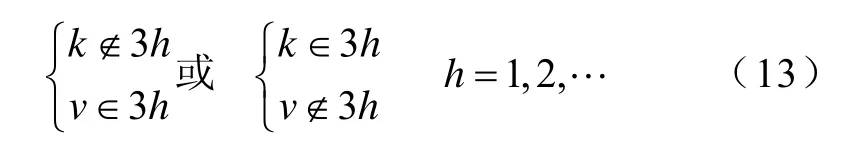
例如：基波电流所产生的空间谐波磁动势v=3,6,9,··和15次谐波电流所产生的空间谐波磁动势v=1,5,7,··等谐波组合均属于该类特点。该类合成磁动势为零，电机中不存在这些次谐波。

实际应用中往往只需知道各次谐波磁动势幅值与基波磁动势幅值的百分比，而不需要计算实际的谐波磁动势幅值，这时先计算出基波磁动势幅值为

式中，p为电机极对数。

然后各次谐波幅值与基波幅值比例为

2 转子损耗的解析分析

电机作为多变量、非线性和强耦合的时空耦合体，每个结构参数的变化都会导致其他参数的变化，要想得到一个转子损耗的确切表达式就必须要综合考虑所有因素，但这样分析的最终模型过于复杂，而且难以从中分析出不同参数的影响，也难以总结出抑制技术和改进措施。本文直接从定子磁动势入手，推导出时间谐波和空间谐波对转子损耗的影响因子。

根据Steinmetz铁耗分离模型，电机铁耗密度可表示为[18]式中，ph、pe分别为磁滞损耗密度和涡流损耗密度；kh、ke分别为磁滞损耗和涡流损耗系数。由于产生转子损耗的谐波磁场一般幅值较小且频率较高，所以在分析时忽略磁滞损耗，仅考虑涡流损耗[1]，那么转子损耗可表示为

故有

为了表征各次时间谐波和空间谐波对损耗的影响大小，以(ω1F1,1)2为基值，各次谐波磁动势对转子损耗的影响因子为

根据前述推导，式（20）可进一步表示为

ξk, v越大，该次谐波对转子损耗的影响就越大。显然，基波电流（k=1）所产生的基波磁场（v=1）的影响因子ξ1,1=0。前面的推导均没有考虑到高次时间谐波电流在转子铁心中的趋肤效应，但谐波频率较高，趋肤效应十分突出，不能忽略。根据透入深度公式可知考虑趋肤效应后谐波磁通所交链的铁心质量约减小到基波磁通所交链的1k。因此，考虑趋肤效应后最终得到影响因子ξk, v为

从式（22）中可以看出，时间谐波电流对转子损耗的影响与谐波幅值Ik的二次方成正比，近似与谐波次数k的1.5次方成正比。在不同极槽配合下，以22次时间谐波电流为例，假设其幅值为基波幅值的3%，对各次谐波的转子损耗影响因子进行对比分析（假设仅含有22次谐波电流，其他次谐波可参照分析）。表1列出了双层绕组不同极槽配合，不同次谐波的转子损耗影响因子。从表中可以看出，不同极槽配合定子绕组磁动势对转子损耗的影响相差很大，下面对表1数据进行详细分析。

表1 不同极槽配合时间谐波和空间谐波对转子损耗影响因素Tab.1 Effect of spatial and time harmonics of different pole/slots combination

1）基波电流对转子损耗的影响

8极9槽电机，基波电流的转子损耗影响因子为ξ1,∑=3.508 2。8极36槽和8极48槽，基波电流的转子损耗影响因子分别为ξ1,∑=0.032 68和ξ1,∑= 0.015 2，分别为8极9槽结构的0.9%和0.43%，这表明8极9槽结构基波电流产生的转子损耗远大于8极36槽和8极48槽结构。

2）时间谐波电流对转子损耗的影响

8极9槽结构，22次时间谐波电流对转子损耗的影响因子为ξ22,∑=0.258 86，为基波影响因子ξ1,∑的7.4%。其中，1次和4次空间谐波的影响最大，分别为ξ22,1=0.095和ξ22,1=0.085，占22次时间谐波电流影响因子ξ22,∑的比例分别为36.8%和32.9%。5次和2次空间谐波的影响次之，分别为ξ22,5=0.042和ξ22,2=0.034，占22次时间谐波电流影响因子ξ22,∑的比例分别为16.3%和13.2%，0.25、0.5、1和1.25次谐波总的影响因子占22次时间谐波电流影响因子ξ22,∑的99.2%。

8极36槽结构，22次时间谐波对转子损耗的影响因子为ξ22,∑=0.085 6，为基波影响因子ξ1,∑的260%。其中，1次空间谐波的影响最大ξ22,1=0.085，占22次时间谐波影响因子ξ22,∑的比例为99.3%。

8极48槽结构，22次时间谐波对转子损耗的影响因子为ξ22,∑=0.084 32，为基波影响因子ξ1,∑的555%。其中，1次空间谐波的影响最大ξ22,1=0.084，占22次时间谐波影响因子ξ22,∑的比例为99.6%。

从三种极槽配合时间谐波电流对转子损耗的影响因子分析可看出，多极少槽（8极9槽）结构，谐波电流所产生的低次空间谐波磁动势（比如8极9槽的1、2、4和5次）对转子损耗的影响最大。每极每相槽数分母为2的分数槽绕组和整数槽绕组（比如8极36槽和8极48槽）时间谐波电流所产生的基波空间磁动势对转子损耗的影响最大。

3）时间谐波电流与基波电流对转子损耗影响的对比

8极9槽结构，基波电流对转子损耗的影响因子占总影响因子的比例为ξ1,∑/(ξ1,∑+ξ22,∑)=93.2%，时间谐波电流影响因子占总影响因子的比例为6.8%。8极36槽结构，基波电流对转子损耗的影响因子占总影响因子的比例为ξ1,∑/(ξ1,∑+ξ22,∑)=27.8%，时间谐波电流影响因子占总影响因子的比例为72.2%。8 极48槽结构，基波电流对转子损耗的影响因子占总影响因子的比例为ξ1,∑/(ξ1,∑+ξ22,∑)= 15.3%，时间谐波电流影响因子占总影响因子的比例为84.7%。

对比分析看出，多极少槽结构（8极9槽）基波电流对转子损耗的影响最大；每极每相槽数分母为2的分数槽绕组和整数槽绕组（比如8极36槽和8极48槽）时间谐波电流所产生对转子损耗的影响最大。

4）不同极槽配合定子电流产生对转子损耗影响的对比

8极9槽、8极36槽和8极48槽结构定子电流基波和22次谐波电流的转子损耗影响因子之和ξ1,∑+ξ22,∑分别为3.767 1、0.118 3、0.099 52，其中8 极9槽结构的影响因子最大，8极48槽结构的影响因子最小，仅为8极9槽结构的2.64%。

以上比例关系虽然是在绕组中仅含有22次电流时间谐波，且幅值为基波3%的情况下得出的，但从中是可以看出，8极9槽类近极槽数的电机转子损耗受电流时间谐波的影响远小于8极48槽类的整数槽结构。同时可以看出，8极9槽类近极槽数电机转子损耗主要受基波电流影响，而8极48槽类整数槽结构转子损耗主要受电流时间谐波影响。

3 转子损耗的有限元分析

图1 几何模型Fig.1 Geometric model

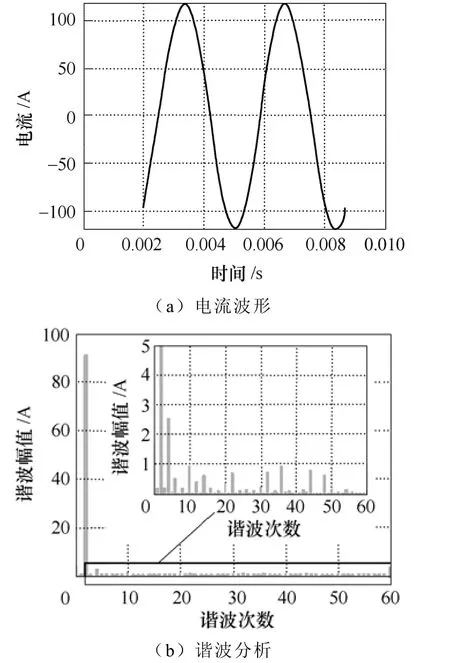
图2 电流波形及谐波分析Fig.2 Current waveform and harmonic analysis

下面对非正弦波供电下20kW 8极9槽和8极48槽两个电机在转子损耗进行有限元分析，验证所提出分析理论的正确性。两台电机的几何模型如图1所示。满载时供电电流波形如图2所示，电流总谐波畸变率为3.8%。计算得到转子q轴上M点和d轴上N点的磁通密度随时间的变化关系如图3和图4所示。从中可以看出，对于8极9槽电机，PWM供电和正弦波供电方式下转子上磁通密度变化差别不大，磁通密度变化的高次谐波较少。而对于8极48槽，PWM供电和正弦波供电时的转子磁通密度变化较大，可以很明显地看出，采用PWM供电后，转子谐波磁通密度的高次谐波分量增加了，这就导致其转子损耗增加。

图3 8极9槽电机M、N两点磁通密度随时间变化关系及谐波分析Fig.3 Flux density vs. time and its harmonic analysis of 8 poles-9 slots of point M and N

图4 8极48槽电机M、N两点磁通密度随时间变化关系及谐波分析Fig.4 Flux density vs. time and its harmonic analysis of 8 poles-48 slots of point M and N

计算得到的不同供电波形下转子损耗随时间变化关系如图5所示。正弦波电压供电和变频器（PWM）供电下的损耗对比见表2，变频器供电时8极9槽和8极48槽结构转子损耗比正弦波电压供电时增加量分别为3.4%和29.6%。这也就说明8极48槽结构转子损耗受时间谐波电流的影响更严重，这与前节中解析分析结果：8极48槽转子损耗受时间谐波电流影响很大，8极9槽转子损耗受基波电流影响大的结论一致，验证了解析分析的正确性。

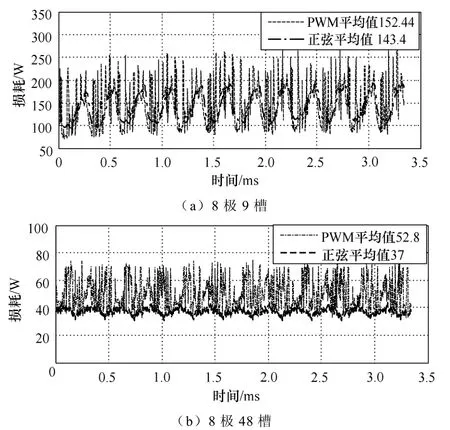
图5 转子损耗随时间变化关系Fig.5 Relationship of rotor loss vs. time

表2 8极9槽和8极48槽转子损耗对比Tab.2 Rotor loss comparison of 8 poles-9 slots and 8 poles-48 slots

4 结论

本文针对整数槽和分数槽绕组在非正弦供电下的定子磁动势所产生的转子损耗进行了解析分析，提出一种用于判断不同极槽配合下定子磁动势谐波对转子损耗影响的转子损耗影响因子：损耗因子越大，所产生的转子损耗越大，反之亦然。损耗因子和有限元分析结果都表明8极9槽类近极槽数电机转子损耗主要由基波电流所产生的空间谐波产生，转子损耗主要受到定子绕组基波电流的影响，时间谐波电流的影响较小。而对于8极48槽类整数槽结构转子损耗更容易受到定子绕组时间谐波电流的影响。

参考文献

[1] Bianchi N, Bolognani S, Fornasiero E. An overview of rotor losses determination in three-phase fractionalslot PM machines[J]. IEEE Transactions on Industry Applications, 2010, 46(6): 2338-2345.

[2] 解恩, 刘卫国, 罗玲, 等. PWM调制对无刷直流电机转子涡流损耗的影响[J]. 电工技术学报, 2013,28(2): 117-125.

Xie En, Liu Weiguo, Luo Ling, et al. Influence of PWM on rotor eddy-current losses in brushless DC motor[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 117-125.

[3] Shen Jianxin, He Hao, Jin Mengjia, et al. Reduction of rotor eddy current loss in high speed PM brushless machines by grooving retaining sleeve[J]. IEEE Transactions on Magnetics, 2013, 49(7): 3973-3976.

[4] Zhao N, Zhu Z Q, Liu W. Rotor eddy current loss calculation and thermal analysis of permanent magnet motor and generator[J]. IEEE Transactions on Magnetics, 2011, 47(10): 4199-4202.

[5] Li Weili, Zhang Xiaochen, Cheng Shukang, et al. Thermal optimization for a HSPMG used for distriuted generation systems[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 474-482.

[6] Li Jian, Choi Da-Woon, Son Dong-Hyeok, et al. Effects of MMF harmonics on rotor eddy-current losses for inner-rotor fractional slot axial flux permanent magnet synchronous machines[J]. IEEE Transactions on Magnetics, 2012, 48(2): 839-842.

[7] 陈益广, 潘玉玲, 贺鑫. 永磁同步电机分数槽集中绕组磁动势[J]. 电工技术学报, 2010, 25(10): 30-36.

Chen Yiguang, Pan Yuling, He Xin. Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 30-36.

[8] Schofield N, Ng K, Zhu Z, et al. Parasitic rotor losses in a brushless permanent magnet traction machine[C]// Proceedings of EMD Conference, 1997: 200-204.

[9] Shah M, Lee S. Rapid analytical optimization of eddy-current shield thickness for associated loss minization in electrical machines[J]. IEEE Transactions on Industrial Applications, 2006, 42(3): 642-649.

[10] Wang J, Atallah K, Chin R, et al. Rotor eddy-current loss in permanent-magnet brushless AC machines[J]. IEEE Transactions on Magnetics, 2010, 46(7): 2701-2707.

[11] Fornasiero E, Bianchi N, Bolognani S. Slot harmonic impact on rotor losses in fractional-slot permanentmagnet machines[J]. IEEE Transactions on Industrial Electronics, 2012, 59(6): 2557-2564.

[12] Miller T J E, McGilp M I, Klontz K W. Approximate methods for calculating rotor losses in permanentmagnet brushless machines[C]//Proceedings of IEEE International Electric Machines & Drives Conference, May 3-6, 2009: 1-8.

[13] Shah M, Lee S. Optimization of shield thickness of finite length rotors for eddy current loss minimizetion[C]//Proceedings of IEEE Industry Applications Society Annual Meeting, Oct. 2006: 2368-2373.

[14] 邢军强. 高速永磁电机转子损耗及通风散热研究[D]. 沈阳: 沈阳工业大学, 2011.

[15] 方程, 许海平, 薛劭申, 等. 直驱型多相永磁同步电机转矩脉动及损耗特性[J]. 电工技术学报, 2014, 29(5): 149-159.

Fang Cheng, Xu Haiping, Xue Shaoshen, et al. Torque ripple and losses of direct-drive multi-phase permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2014, 29(5): 149-159.

[16] Nerg J, Niemelä M, Pyrhönen J, et al. FEM calculation of rotor losses in a medium speed direct torque controlled PM synchronous motor at different load conditions[J]. IEEE Transactions on Magnetics, 2002, 38(5): 3255-3257.

[17] Yamazaki K, Kanou Y. Rotor loss analysis of interior permanent magnet motors using combination of 2-D and 3-D finite element method[J]. IEEE Transactions on Magnetics, 2009, 45(3): 1772-1775.

[18] Yamazaki K, Kato Y, Ikemi T, et al. Reduction of rotor losses in multi layer interior permanent-magnet synchronous motors by introducing novel topology of rotor flux barriers[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3185-3193.

[19] Jae-Do Park, Kalev C, Hofmann H F. Analysis and reduction of time harmonic rotor loss in solid-rotor synchronous reluctance drive[J]. IEEE Transactions on Power Electronics, 2008, 23(2): 985-992.

沈启平 男，1983年生，博士，讲师，研究方向为特种电机的设计及控制和新能源驱动电机开发。

E-mail: shenqp1983@cqu.edu.cn（通信作者）

韩雪岩 女，1978年生，女，副教授，硕士生导师，研究方向为特种电机、电磁场分析等。

E-mail: hxyslm@163.com

作者简介

收稿日期2014-10-15 改稿日期 2015-03-09

中图分类号：TM351