阶梯轴轴肩过渡曲线优化研究

任晨峰

（华北电力大学 能源动力与机械工程学院，保定 071000）

阶梯轴轴肩过渡曲线优化研究

任晨峰

（华北电力大学 能源动力与机械工程学院，保定 071000）

提出二次曲线+圆弧的过渡曲线理论，利用其代替阶梯轴原有的单一形式过渡曲线以及其他含有类似过渡区域零件的过渡曲线，以降低零件局部的应力集中，起到提高使用寿命的作用。以阶梯轴为例，建立二次曲线+圆弧的过渡曲线方程，并进行有限元优化分析。分析结果表明，新的过渡曲线可以有效降低轴肩过渡区域的应力集中。

形状优化 过渡曲线 二次曲线 圆弧 应力集中

应力集中是指物体中局部应力骤增的现象，通常发生在物体形状发生急剧变化的部位。拥有轴肩过渡处的阶梯轴的主要失效原因，是轴肩过渡处由于形状改变而出现的应力集中。阶梯轴的过渡曲线，通常采用四分之一圆弧。为了减小其应力集中现象，文献[1-2]提出利用三次样条代替原有圆弧。文献[3]采用双曲线型线及流线型线作为阶梯轴的过渡曲线。文献[4]则提出利用双指数“超圆”和“超椭圆”曲线族来描述过渡曲线。文献[5]则是以万向十字轴为例，总结并对比了使用双曲率曲线、流线型曲线、椭圆形曲线三种曲线后，轴根过渡处的应力集中程度。以上表明，单从形状上寻求最优曲线以降低阶梯轴轴肩处的应力集中是可行的。

1 圆弧过渡曲线

由于阶梯轴是关于轴线对称的回旋体，在分析时为了缩短分析时间，可将其简化为对称问题。以阶梯轴为分析对象，该阶梯轴在直线EF处受到垂直向下均布压力100N。阶梯轴上的C点、D点之间是一段由半径为15mm的四分之一段圆弧构成的过渡曲线，则圆弧过渡曲线为：

利用有限元软件计算得到应力云图，该零件在上述描述的工况下的最大应力，出现在过渡曲线中距离C点较近处，为127.051MPa。

2 二次曲线+圆弧过渡曲线

光滑的过渡曲线首先需要满足曲线两端与零件相切，在建立的坐标系中，相切即为建立的新的过渡曲线段，在C、D两点处需满足由线段BC和DE确定的函数值与斜率值条件，即：

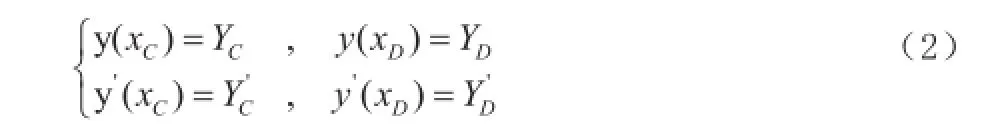
其中，y(x)为过渡曲线函数，YC、YD和yC´、yD´分别为坐标系中C点和D点在线段BC和DE上的函数值以及斜率值。

若利用多项式建立过渡曲线，则根据4个约束条件，多项式的次数至少需要由3次，即：

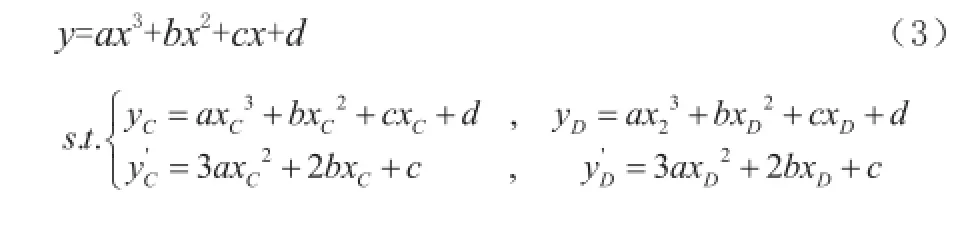
而要将函数中的相关系数设计为变量，则至少需要将函数的阶数提高至4阶，共5个变量。但是，过多的设计变量会导致计算量的骤增，难以找到最优解。根据应力云图的特点，在受力时，轴肩曲线上出现最大应力的位置距离C点较近，说明该处对于荷载较为敏感，而距离D点附近的应力则明显小于最大应力值。根据这一特点，利用二次曲线代替距离横截面较小的曲线段。同时，为了满足曲线末端的约束条件，继续利用圆弧作为距离横截面较大处的过渡曲线。为了保持过渡曲线的光滑性，使二者在曲线的某处相切。这样过渡曲线中就只有两个设计变量，即二次项的系数a与圆弧的半径R，过渡曲线形式如下：

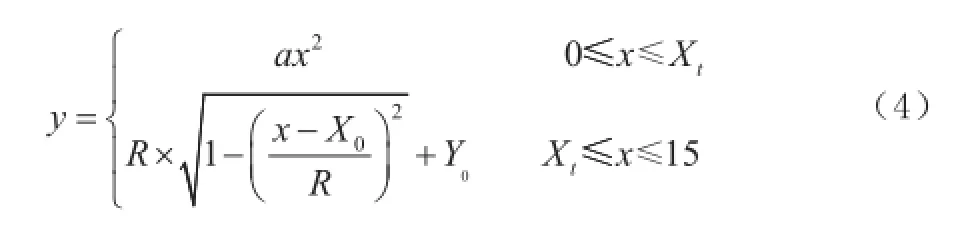
根据上述内容建立本次研究的优化模型如下。

优化目标：min{max(YL)}

设计变量：a、R

约束条件：S(x1)=y1，S(x2)=y2，S´(x1)=y1´，S´(x2)=y2´，其中YL为过渡曲线中的最大应力。

利用ANSYS软件中的优化工具，对模型进行求解并得到最优解。最优解和其相对应的变量值，如表1所示。

表1 优化结果

此时，对应的过渡曲线为：

优化后过渡曲线上的最大应力值为115.57MPa，相较原有过渡曲线时的最大应力127.051MPa，下降了9.04%。

3 结论

本文以一阶梯轴为例，介绍了一种利用二次曲线+圆弧的轴肩过渡曲线代替原有圆弧过渡曲线的方法。将二次曲线中的二次项系数和圆弧的半径设定为优化变量，以轴肩过渡曲线上的最大应力值为优化目标，利用ANSYS中的优化工具，得到在满足约束条件下的最优解。优化后的轴肩过渡区域的应力集中相较原有形状有所下降。

[1]吴凤林，任家骏.轴肩过渡曲线形状设计研究[J].中国机械工程，1998，9（9）.

[2]罗亚波，张晓东.轴肩过渡曲线形状优化研究[J].武汉理工大学学报：交通科学与工程版，1999，（5）：492-495.

[3]西田正孝.应力集中[M].北京：机械工业出版社，1986.

[4]芮井中.具有最小应力集中的缺口形状优化方法研究[D].扬州：扬州大学，2009.

[5]陈科，殷磊，陈振华.万向十字轴轴根过渡结构的优化设计和分析[J].中国机械工程，2014，（23）.

Research on the Optimization of Shoulder Transition Curve of Stepped Shaft

REN Chenfeng
(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071000)

In order to reduce the stress concentration and improve service life.Establish a theory of transition curve which contains both conic and arc.Use the new curve to replace the traditional shoudler transition curve of stepped shaft and other parts like that.Take a stepped shaft as an example,and establish the transition curve equation and use the FEM analysis to optimise the curve.The result indicates that the new stress concentration is relieved by using the new transition curve.

shape optimization,transition curve,conic,arc,stress concentration