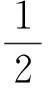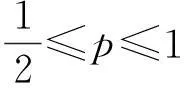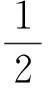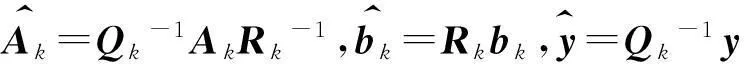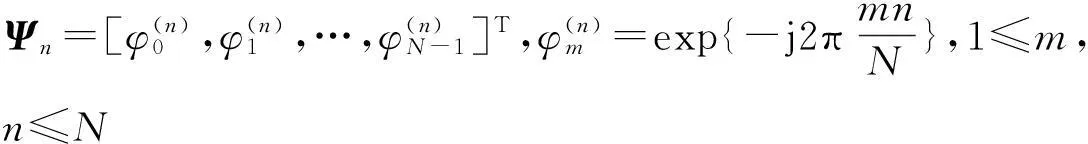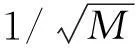基于欠定系统局灶解法的逆合成孔径雷达成像
2016-04-07童宁宁冯为可胡小伟
江 东,童宁宁,冯为可,胡小伟
(空军工程大学防空反导学院, 陕西 西安 715100)
基于欠定系统局灶解法的逆合成孔径雷达成像
江东,童宁宁,冯为可,胡小伟
(空军工程大学防空反导学院, 陕西 西安 715100)
摘要:针对目前压缩感知中常用的信号重构算法普遍存在计算复杂、需要信号的稀疏度作为先验信息等缺陷的问题,提出了基于欠定系统局灶解法(Focal Undetermined System Solver, FOCUSS)的逆合成孔径雷达(Inversed Synthetic Aperture Radar, ISAR)成像方法。该方法利用QR分解预处理共轭梯度法求解正则化FOCUSS算法中的线性方程组,在不需要先验信息的条件下进一步提高算法收敛速度。仿真实验表明,利用基于QR分解预处理共轭梯度法改进的正则化FOCUSS算法对回波信号进行重构,既能获得更加清晰的成像结果,又能进一步提高运算速度。
关键词:压缩感知;逆合成孔径雷达;欠定系统局灶解法;信号重构
0引言
高分辨雷达成像技术在目标识别、航空管制等军事和民用领域有着广泛的应用,而要获得高分辨的雷达图像,通常需要采用大信号带宽。但是瞬时带宽大,对雷达系统的A/D转换速率及数据处理等有较高要求。近年来信号处理领域中提出的压缩感知[1-4](Compressive Sensing,CS)理论指出,当信号具有稀疏性或可压缩性时,通过求解一个最优化问题,就可以依靠远低于Nyquist率所采集到的信号测量值实现信号的准确或近似重构。而对于ISAR成像而言,由于目标强散射点数远小于采样数,目标回波满足稀疏性的条件。因此,CS理论可以缓解直接对目标回波进行带通采样带来的数据采集和存储压力,为高分辨雷达成像提供了一种新的途径。
将CS理论应用于雷达成像[5-6]的关键在于能否利用合适的重构算法实现对原始信号的精确重构。文献[7—9]分别提出利用凸优化、贪婪追踪及其组合算法对信号进行重构。凸松弛算法需要的测量数最少、精度高,但有繁重的计算负担;贪婪追踪算法运算复杂度较低,但需要信号的稀疏度作为先验信息且抗噪能力较差。本文针对此问题,提出了基于欠定系统局灶解法(Focal Undetermined System Solver, FOCUSS)的逆合成孔径雷达(Inversed Synthetic Aperture Radar, ISAR)成像方法。
1压缩感知理论及FOCUSS算法基本原理
1.1压缩感知理论
考虑一个有限长度的一维实值离散信号x∈RN×1,如果x可以表示为:
x=Ψα
(1)
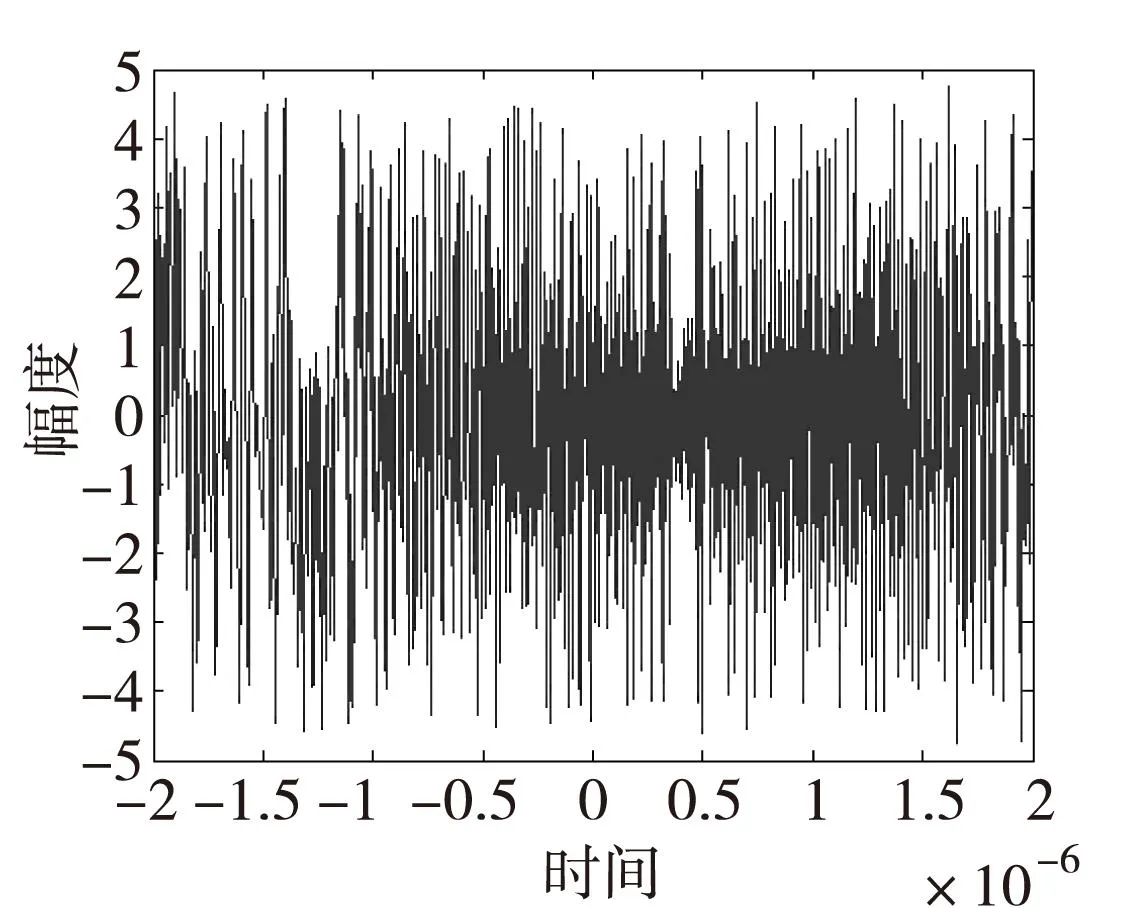
式(1)中α为N×1维列向量,Ψ=[ψ1,ψ2…,ψN],ψi为N×1维的基向量。如果x仅表示为K个基向量的线性组合,换句话说如果α中仅有K个元素不为零,其他的元素都为零时,则称信号x是K-项稀疏的,或者称信号的稀疏度为K。
压缩感知理论指出,当信号x在某一稀疏基ψ上是稀疏的,则可用一个与ψ不相关的M×N维观测矩阵Φ(K yM×1=ΦM×NxN×1=ΦM×NΨN×NαN×1 (2) 由式(2)易知,观测值y的维数远小于x的维数,从而实现了对信号的压缩采样。 式(2)中α的求解可归结为如下一个l1范数最小化问题 (3) 式(3)中,Γ=ΨΦ。 考虑到运算复杂度和先验信息等问题,本文提出利用FOCUSS算法对式(3)中的最优化问题进行求解。 1.2FOCUSS算法基本原理 FOCUSS算法又名欠定系统局灶解法,其实质上是一种加权最小范数最小二乘法。FOCUSS算法利用后验知识,采用逐步迭代的方法,由前一次计算求得的迭代数据产生新的加权函数,利用新的加权函数求得迭代数据使得能量较上一步更为集中。FOCUSS算法的核心在于通过线性变换α=Wq将方程(4)转化为约束最优问题: min‖q‖2s.t.‖y-ΓWq‖2=0 (4) 式(4)中,W表示权值矩阵,q表示约束最小解。 然后用拉格朗日乘子将约束最优问题转化为非约束问题: (5) 式(5)中,λ为正则化系数,与噪声水平有关。 再对C(q)求偏导数,并令其为零,从中求得q值为: q=WHΓH(ΓWWHΓH+λI)-1y (6) 将q值代入式α=Wq,得到: α=WWHΓH(ΓWWHΓH+λI)-1y (7) 将FOCUSS算法转化为实际求解问题的迭代过程描述如下: 1)初始化 取α0=ΓHy作为迭代初始化值,αk-1为第k-1次迭代值,且αk-1=[αk-1(1),αk-1(2),…,αk-1(N)]T 2)计算权值矩阵Wk (8) 3)迭代运算 更新αk,即: αk=WkWkHΓH(ΓWkWkHΓH+λI)-1y (9) 4)如果αk满足收敛条件,迭代停止,否则返回1)。 2基于改进FOCUSS算法的压缩感知ISAR成像 2.1改进的FOCUSS算法 本文在深入研究线性方程组求解的预处理方法的基础上,利用QR分解预处理共轭梯度法求解线性方程组对正则化FOCUSS算法进行改进,提高了算法收敛速度。具体实现过程如下: 1)初始化 取α0=ΓHy作为迭代初始化值,αk-1为第k-1次迭代值,且αk-1=[αk-1(1),αk-1(2),…,αk-1(N)]T 2)计算权值矩阵Wk 3)迭代运算 ①对系数矩阵进行近似分解。 根据矩阵分解理论,Ak能够化成正交(酉)矩阵Qk和非奇异上三角矩阵Rk的乘积,即: Ak=QkRk (10) ②对线性方程组进行预处理。 取预处理矩阵为QkRk,则Akbk=y等价为: (QkRk)-1Akbk=(QkRk)-1y (11) 对式(9)乘矩阵Rk-1得到: (12) ③求解线性方程组 (13) 4)如果αk满足收敛条件,迭代停止,否则转到1)。 2.2基于FOCUSS算法的压缩感知ISAR成像 设雷达发射脉宽为Tp,带宽为B的线性调频脉冲信号为 (14) 设目标包含I个散射点,则目标回波可以表示为: (15) 式(15)中,δi为第i个散射点的散射强度,τim(tm)=2Ri(tm)/c为对应散射点的时延,其中,Ri(tm)为tm时刻该散射点到雷达的距离,c为电磁波传播速度。 设参考信号为: (16) 式(16)中,τ0=2Rref/c为参考延时,Rref为参考距离。 采用Stretch处理,即回波信号与参考信号做差频得 (17) 式(17)中,Δτim=τim-τ0。 由上式可知,Stretch处理后各散射点回波的相位为 (18) 设α为sif在频域的稀疏系数,分别构造离散傅里叶矩阵Ψ,由sref构成的N×N对角矩阵Θ,即 (19) (20) 其中m,n分别为元素在矩阵中的行、列序号,1≤m,n≤N。 则式(17)可表示为: sif=ΘHsr=Ψα (21) 由于ΘH=Θ-1,所以式(19)可表示为: sr=ΘΨα=Dα (22) 式中,D=ΘΨ。 由式(22)可得: 1)sr=Dα,即D为回波sr的稀疏基; 2)DHD=(ΘΨ)H(ΘΨ)=ΨHΘHΘΨ=I即D具有正交性。 因此,D为回波sr的正交稀疏基。 为了保证在观测过程中不丢失重要信息,能准确重构原始信号,观测矩阵Φ和稀疏矩阵D需满足不相关的要求,即观测矩阵Φ需要满足约束等距性准则(Restricted Isometry Property, RIP),实验证明,如随机高斯矩阵、伯努利矩阵等随机矩阵都能较好地满足上述要求。文中采用的是随机高斯矩阵。 (23) 它的优点在于它几乎与任意稀疏信号都不相关,因而所需的测量次数最小,但缺点是矩阵元素所需存储空间很大。随机高斯测量矩阵测量值的数目M须满足: M>cKlg(N/K) (24) 其中c是一个很小的常数。 N维回波信号经过随机高斯测量矩阵Φ降维处理之后得到的M维观测信号的过程可表示为: yM×1=ΦM×NsrN×1=ΦM×NDN×NαN×1=ΓM×NαN×1 (25) 式(25)中α的求解可归结为如下一个l1范数最小化问题 (26) 实际雷达回波信号通常是非理想稀疏或被噪声污染的,重构过程转化为如下具有松弛约束的l1范数最小化问题: (27) 式(27)中ε由回波数据中的噪声量决定。 本文提出利用FOCUSS算法对回波信号进行重构。 以上讨论主要是针对ISAR成像中距离向数据采集展开的,方位向可采用传统FFT方法处理,也可采用CS方法处理。 3仿真实验结果及分析 为验证文中方法的有效性和可行性,下面使用MATLAB语言进行有关仿真实验。设雷达载频为10GHz,带宽为300MHz,脉宽为4μs,采样频率为300MHz,脉冲重复频率为50Hz,距离向采样点数N=1 200,方位向采样点数M=250。设计一个具有5个强散射中心的模拟目标,假设散射强度均为1 ,雷达与目标中心距离为10 000m,散射点坐标分别为(48,0)、(0,48)、(0,-48)、(-96,48)、(-96,-48),其散射点分布及原始雷达回波信号波形如图1、图2所示。 图1 仿真目标散射点分布Fig.1 The scattering point of the target 图2 原始雷达回波信号波形Fig.2 The waveform of original radar echo 转台模型中,目标旋转角速度为0.01rad/s,距离分辨率和方位分辨率均为1m,成像积累时间为5s,成像积累角度为0.05rad/s,用传统RD算法成像结果如图3所示。 图3 FFT成像结果Fig.3 The image via FFT 对于ISAR成像,距离向采用CS方法,方位向既可采用传统FFT方法也可采用CS方法进行处理。为简化运算,在本文中距离向采用CS方法,方位向采用传统FFT方法。分别采用正则化FOCUSS算法和利用QR分解预处理共轭梯度法改进的正则化FOCUSS算法进行信号重构。成像结果如图4所示。 图4 基于CS的成像结果Fig.4 The image via CS 通过对比图3、图4的成像结果可得,与传统成像算法相比,基于CS的成像方法能够利用较少的测量数据获得聚焦质量更好的图像;特别是利用改进的正则化FOCUSS算法的成像方法得到的结果更清晰。 此外,利用QR分解预处理共轭梯度法改进的正则化FOCUSS算法,在不需要先验信息的条件下能进一步提高算法收敛速度。本文通过对仿真过程的分析,在设定停止迭代误差限值为1×10-10的情况下,得出了正则化FOCUSS算法和利用QR分解预处理共轭梯度法改进的正则化FOCUSS算法停止迭代时所需迭代步数和迭代误差。分析结果如表1所示。 表1 两种方法的迭代步数和迭代误差 从表1中可以看出:正则化FOCUSS算法需要较高的迭代次数才能够满足成像误差的要求,而基于QR分解预处理共轭梯度法改进的正则化FOCUSS算法仅仅经过一步迭代,成像误差便远小于设定值。因此基于QR分解预处理共轭梯度法改进的正则化FOCUSS算法可以利用单步运算的时间获得很高的成像质量,兼顾了单步算法和迭代算法的优点,是一种快速而且高效的单步成像算法。 4结论 本文提出了基于FOCUSS算法的ISAR成像方法。该方法利用QR分解预处理共轭梯度法求解正则化FOCUSS算法中的线性方程组,在不需要先验信息的条件下进一步提高算法收敛速度。仿真实验表明,利用基于QR分解预处理共轭梯度法改进的正则化FOCUSS算法对回波信号进行重构,既能获得更加清晰的成像结果,又能进一步提高运算速度。 参考文献: [1]MatthewHerman,ThomasStrohmer.Highresolutionradarviacompressedsensing[J].IEEETransactionsonSignalProcessing, 2009, 57(6): 2275-2284. [2]JoachimHGEnder.Oncompressivesensingappliedtoradar[J].IEEETransactionsonSignalProcessing, 2010, 90(5): 1402-1414. [3]LiJun,XingMengdao,ZhangLei,etal.HighresolutionimagingmethodforthesparseapertureofISAR[J].JournalofXidianUniversity(NaturalScience), 2010, 37(3): 441-446. [4]QuanYinghui,Zhanglei,LiuYabo,etal.MethodforachievinghighresolutionISARimagingwithshortaperturedataviacompressedsensing[J].JournalofXidianUniversity(NaturalScience), 2010, 37(6): 1022-1026. [5]HUChenxi,LIUYimin,LIGang,etal.ImprovedFOCUSSmethodforreconstructionofclusterstructuredsparsesignalsinradarimaging[J].SciChinaInfSci, 2012, 55: 1776-1788. [6]RaoBD,EnganK,CotterSF,etal.Subsetselectioninnoisebasedondiversitymeasureminimization[J].IEEETrans.onSP, 2013, 51(3): 760-770. [7]TroppJA,WrightSJ.ComputationalMethodsforSparseSolutionofLinearInverseProblems[R].US:CaltechACMTech.Rep,2009. [8]DoThongT,GanL,NguyenN,etal.Sparsityadaptivematchingpursuitalgorithmforpracticalcompressedsensing[C]//AsilomarConferenceonSignals,Systems,andComputers,PacificGrove.California,2008,581-589. [9]刘记红,徐少坤,高勋章,等. 基于压缩感知的LFM雷达成像方法[J]. 数据采集与处理,2012,11(27):284-290. [10]ZhaoshuiHe,AndrzejCichockj,RafalZdunek,etal.ImprovedFOCUSSMethodWithConjugateGradientIterations[J].IEEETrans.onSP, 2009, 57(1): 399-404. ISAR Imaging Algorithm Based on Focal Undetermined System Solver Method JIANG Dong, TONG Ningning, FENG Weike, HU Xiaowei (Air and Missile Defense College, Air Force Engineering University, Xi'an 710051, China) Abstract:In order to solve the problems of the existing signal reconstruction methods which have more or less defects such as big amount of calculation and needing the signal sparseness as the prior information, an improved method of ISAR imaging algorithm based on focal undetermined system solver was proposed. Of this method, conjugate gradient scheme based on QR decomposition was used to solve the linear equations in regularized focal undetermined system solver (R-FOCUSS) method. Simulation results showed that it could obtain more clear imaging results and further improved the computing speed by using the improved method to reconstruct the received signal. Key words:compressed sensing; inversed synthetic aperture radar; regularized focal undetermined system solver; signal reconstruction 中图分类号:TN95 文献标志码:A 文章编号:1008-1194(2016)01-0099-05 作者简介:江东(1991—),男,湖南常德人,硕士研究生,研究方向:雷达信号处理。E-mail:jd__283945288@163.com 基金项目:国家自然科学基金项目资助(61372166);陕西省科学基金项目资助(2014JM8308) *收稿日期:2015-09-17