红外探测与追踪的双机被动定位模型
2016-04-07郝振兴罗继勋胡朝晖李文超
郝振兴,罗继勋,胡朝晖,李文超
(1.空军工程大学航空航天工程学院,陕西 西安 710038;
2.解放军95896部队,河北 沧州 061736)
红外探测与追踪的双机被动定位模型
郝振兴1,罗继勋1,胡朝晖1,李文超2
(1.空军工程大学航空航天工程学院,陕西 西安 710038;
2.解放军95896部队,河北 沧州 061736)
摘要:针对机载红外探测与追踪(IRST)被动定位的精度低和解算速度慢及多机间信息大容量实时传输问题,提出了两种应用激光数据链传输信息的IRST双机被动定位模型。模型均基于测向交叉定位原理构建,模型一的基线距离已知,两机坐标未知;模型二的两机坐标已知,基线距离未知;并对比了两种模型的特性。仿真表明,测角误差减小,两机距离增大,会提高定位精度;模型二的计算速度优于模型一,但目标高度大于1 km时,模型二失效;双机与目标构成等腰三角形且两载机的交角为110°时,定位的精度最高。
关键词:激光数据链;机载红外探测与追踪;测向交叉定位;几何精度因子
0引言
被动(无源)探测定位系统利用目标辐射源的辐射信息探测目标并确定出目标位置,具有作用距离远、隐蔽性能好等优点,在现代信息化战争中有着广泛的应用前景[1]。机载IRST系统被动定位一般分为单机和多(双)机平台的被动定位。文献[2]研究了IRST单站被动定位系统问题,分析了单站被动测距的几种典型算法。但是对于运动目标,单机必须做适当的机动,满足可观测条件才能实现对目标的定位跟踪,单机红外搜索跟踪系统探测精度也因电子干扰技术的进步、隐身技术的突破性进展而降低。文献[3]建立了双机协同探测定位跟踪模型,利用双机IRST系统探测到目标方位角和俯仰角,结合非线性滤波算法估计出目标位置信息,但该算法的解算占用较多的计算机资源和时间,而且一般的机间射频通信不仅无法实时传输大容量的原始红外图像信息,在一定程度上还破坏了“隐蔽性”。文献[4]提出基于激光链路的IRST信息处理方法,机载激光数据链能满足海量图像信息量传输和隐蔽性要求。文献[5-6]分别提出针对IRST探测跟踪目标并提取信息的滤波算法。文献[7]针对无源同高度固定双站测向交叉定位原理与精度进行了初步分析,给出了影响精度的部分因素。为此,在上述文献研究成果的基础上,本文针对机载IRST被动定位的精度低和解算速度慢及多机间信息大容量实时传输问题,提出了应用激光数据链进行信息传输,基于测向交叉定位原理的两种IRST双机被动定位模型。
1定位理论
1.1应用激光通信链路的双机IRST被动定位原理
应用激光通信链路的被动定位方法是先检测出融合图像中存在的目标个数,然后计算目标相对于观测载机的测向线,因此不存在测向线相交而产生的虚假目标,提高了多目标被动定位的准确性。图1为原理图。

图1 应用激光数据链路的被动定位原理图Fig.1 Passive locotion principle of laser data chains
假设长、僚机编队飞行,协同探测同一目标区域,且IRST系统独立工作,长机的融合中心将同一场景不同视角的两幅红外图像进行预处理、变换空间、像素级融合等操作,导出更有效、更全面的红外图像,再根据目标与背景图像的差别检测出目标在图像中的位置信息[8-9]。结合长、僚机的状态信息、IRST系统相对于目标的偏角,利用测向交叉定位原理就能得到目标的距离信息。
其中,载机自身运动参数通过机载测量设备测得。僚机的所有数据信息通过激光数据链路传输到长机的融合中心,长机的所有数据信息通过机载光纤总线传到融合中心。
1.2测向交叉定位原理
多机IRST测向交叉定位是利用多个机载IRST系统同一时间测得同一目标的高精度测向线,通过计算各测向线在空间中的交点来确定目标的位置。这里以双机为例,长机、僚机和目标的二维空间位置如图2所示。

图2 双机测向交叉定位原理Fig.2 Triangalation location of two planes
长机坐标为(x1,y1),僚机坐标为(x2,y2),两机所测得同一目标T(xT,yT)的方位角分别为θ1、θ2。由图中的几何关系可得:
(1)
O1s的长度可表示为:
(2)
目标坐标为:
(3)
2定位几何模型及误差
2.1基线距离已知,两机坐标未知
如图3所示,O1、O2为长机和僚机的位置O1O2=d,已知,O2′为O2在xO1y面内的投影,S′为目标在xO1y面内的投影,S″为目标在僚机坐标平面内的投影。目标S坐标为(xT、yT、zT)。
L1、L2为目标到两机的斜距,α1、α2分别是两机测得目标的方位角,β1、β2分别为两机测得目标的俯仰角。α3、β3分别是僚机相对于长机的方位角和俯仰角。
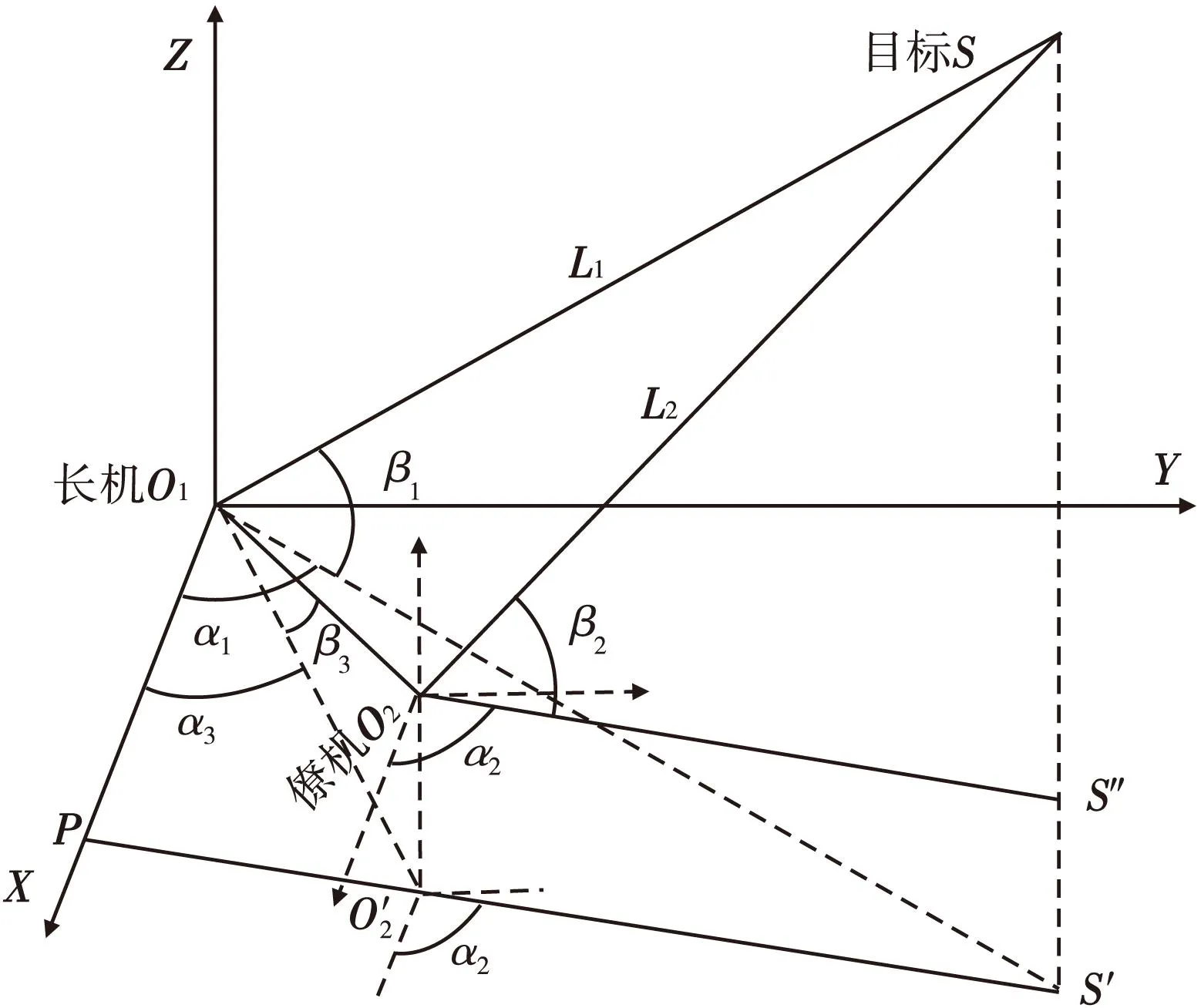
图3 双机定位示意图(一)Fig.3 Two planes location sheme(one)
根据图3中几何关系可得目标的坐标为:
(4)
2.2两机坐标已知,基线距离未知


图4 双机定位示意图(二)Fig.4 Two plane location sheme(two)
则由图4中的几何关系可得目标的坐标为:
(5)


2.3定位误差公式推导
从统计学的角度看,由于载机测向系统的随机噪声产生测量误差,即实际测量过程中得到的方位与俯仰角αi、βi(i=1,2),存在误差,这个测量误差引起定位误差,定位点在真实位置周围就会随机散布。文献[10—11]中提出,几何稀释精度是衡量定位精度的常见指标。
“定位精度的几何稀释”即GDOP,用于描述三维分布下的定位误差,定义如下:
(6)
其中,σx、σy、σz为三维定位的均方差。
利用上述的描述,可对长机、僚机测向交叉定位误差进行分析。为了方便分析,假设:长机、僚机所配置传感器的精度指标相同;不考虑惯导误差;载机各误差之间不相关。
模型一:基线距离已知,两机坐标未知。
对式(4)求偏导,
(7)
式中,
式(7)可以写成:
dX=HdZ
(8)
式中,H=[Hx,Hy,Hz]T

P为定位误差的协方差,则有:
(9)
可得x、y、z轴的定位精度:
GDOP表示为:
(10)
模型二:两机坐标已知,距离未知。
对式(5)求偏导,同样可得目标定位误差的方差,并求得双机在三维几何分布下的定位误差GDOP。
P为定位误差的协方差,则有:
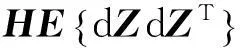
(11)

3仿真分析
双机进行超视距协同空战时,当完成近距引导,开始接敌实施攻击的准备过程中,对目标定位精度的高低直接影响可控武器的脱靶量大小。因此,有必要对两种定位模型的精度进行仿真解算,得到每个模型的精度以及模型精度的影响因素,从而对比模型的特性,给出模型的适用条件。
定义长机所在的水平面为目标高度的基准面。以下结论均是在不同条件下对每一模型的GDOP进行1 000次蒙特卡洛仿真得到的。
对于模型一,假设长、僚机间距离为60 km,且在同一高度,距离测离误差为σd2=0.2 m,方位角与俯仰角测量误差的均方差为σα1=σα2=σα3=σα,σβ1=σβ2=σβ3=σβ,且σα=σβ,目标在x,y轴的变化是[-100,100]、[-100,100],单位为km。图5绘制了测角误差分别为σα2=0.1 mrad、σα2=0.9 mrad、σα2=1 mrad的定位精度分布图。从图中可以看出:随着测角误差的增大,定位精度明显下降,测角误差对定位精度产生了主要影响。

图5 测角误差影响Fig.5 Angle measuring error in fluence
图6绘制了测角精度同为σα2=0.9 mrad,距离误差σd2=0.2 m两机距离分别为d=20 km、40 km、60 km的定位精度分布图。从图中可以看出:随着两机距离的增大,定位精度明显上升,两机距离对定位精度产生了主要影响。
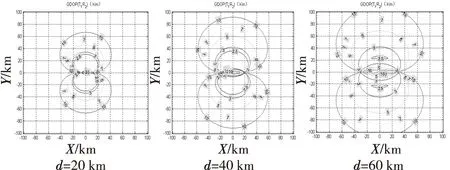
图6 两机距离影响Fig.6 Two plane distance in fluence
图7绘制了测角精度同为σα2=0.9 mrad,距离误差σd2=0.2 m,两机距离分别为d=40 km,目标高度分别为h=100 m、1 000 m、10 000 m的定位精度分布图。从图中可以看出:目标高度不是影响定位精度的主要因素。

图7 目标高度影响Fig.7 Target height in fluence
图8绘制了测角精度同为σα2=0.9 mrad,两机距离分别为d=40 km,目标高度分别为h=100 m,两机距离误差σd2=0.2 m、σd2=0.02 m、σd2=0.002 m的定位精度分布图。从图中可以看出:距离误差不是影响定位精度的主要因素。

图8 距离误差影响Fig.8 Distance error in fluence
对于模型二,给定与模型一相同的参数可以得到在不同的条件下类似的结果,此处不再赘述。
在图9中可知,当目标高度位于1 km时,模型一的定位精度优于模型二,模型二在长机区域误差梯度加大,在僚机区域算法失效。对于模型一如图7目标高度位于10 km时,僚机区域的误差梯度加大。

图9 两种模型的GDOP分布图Fig.9 GDOP of two models
在超视距空战战场信息不完全可知的条件下,应首先确保准确的测量出基线距离,选取模型一完成作战任务。
从两种模型的GDOP分布图还可以看出,GDOP等值线从基线向外扩展,定位精度开始从大到小,到达载机中垂线位置时,又由小到大。在基线的延长线上,定位精度最差。说明当长机与僚机与目标构成一个等腰三角形时,定位精度最高。
进一步分析长机与僚机与目标构成怎样的三角形形状,才能使定位的误差达到最优。对式(11)求导:
又因为α1=α2,可求得:α1≈35°,即目标在长机与僚机中垂线上,且与两机的方位角约为35°时,定位精度最高,该结论与文献[12]中的结论相符。
4结论
本文提出了两种基于测向交叉定位原理的IRST双机被动定位几何模型,模型一的基线距离已知,两机坐标未知;模型二的两机坐标已知,基线距离未知;并针对载机定位误差进行了分析和仿真,得到了两种模型测向交叉定位的绝对误差GDOP仿真图。通过仿真初步得出结论:在满足多机间大容量实时传输和隐蔽性要求的基础上,模型二的计算速度明显优于模型一,但在目标高度大于1km时,模型二失效;长机与僚机的位置构成一个等腰三角形且两载机的交角为110°时,定位的精度最高;测角误差减小,两机距离增大时,定位精度也会提高很快。下一步需进一步理论分析模型二失效的原因以及误差与精度的定量关系。
参考文献:
[1]孙仲康,郭福成,冯道旺.单站无源定位跟踪技术[M].北京:国防工业出版社,2008.
[2]梁捷,谢小方,曹建,等.机载多点测向交叉定位的最优机方向研究[J].电光与控制,2010,17(10):14-17.
[3]张平,方洋旺,朱剑辉,等.基于UKF算法的双机协同无源跟踪[J].电光与控制,2012,19(4):26-30.
[4]陈鑫,王海晏,徐强,等.基于激光通信链路的机载IRST被动定位方法[J].电光与控制,2013,20(6):40-44.
[5]于振红,朱振福,江荣熙,等.基于双门滤波的红外点目标检测方法[J].系统工程与电子技术,2004,26(9):1195-1197.
[6]吴盘龙,陈风,王宝宝.基于鲁棒H∞滤波的多站角度测量机动目标被动跟踪[J].系统工程与电子技术,2011,33(1):17-20.
[7]刘军,曾文锋,江恒,等.双站测向交叉定位精度分析[J].火力与指挥控制,2010,35(S):12-14.
[8]徐强,王海晏,杨海燕,等.激光数据链路与IRST信息融合方法研究[J].应用光学,2013,34(2):349-354.
[9]徐强,王海晏,杨海燕,等.双机IRST配准融合图像的弱小目标检测方法[J].应用光学,2013,34(6):1025-1029.
[10]WANGBC,HEY,WANGGH.RelatedIssuesinDual-sensorBearing-onlyLocalization[J].Opto-ElectronicEngineering,2012,39(1):80-87.
[11]武宜川,潘冠华,罗双喜.空基平台无源定位精度分析[J].指挥控制与仿真,2010,32(2):89-92.
[12]王本才,何友,王国宏,等.双站无源定位最佳配置分析[J].火力与指挥控制,2012,37(2):120-123.
Two-fighter Passive Location Model for Infrared Search and Track
HAO Zhenxing1,LUO Jixun1,HU Zhaohui1,LI Wenchao2
(1.Engineering College of Aeronautics and Astronautics, Air Force Engineering University,Xi’an 710038, China;2.Unit 95896 of PLA, Cangzhou 061736, China)
Abstract:For the problem of low accuracy, settlement calculation speed and large capacity information real-time transmission of airborne infrared search and track (IRST) among multiple machine problem, two application laser data link transmission information of IRST passive positioning of two models were put forward. The models were built on the basis of the principle of direction of arrival location, a baseline distance was known and aircraft coordinates unknown. Simulation results showed that the measuring angle error was reduced, the positioning accuracy was improved when the two machine distance increased; the computing speed of model two was better than model one, but, when the target height was greater than 1 km, model two failed; when two aircrafts and target forming a isosceles triangle and the two aircraft crossing angle was 110 °, the highest accuracy was gained.
Key words:laser link; airborne infrared search and track (IRST); directing of arrival (DOA) location; geometrical dilution of precision (GDOP)
中图分类号:V271.4
文献标志码:A
文章编号:1008-1194(2016)01-0028-05
作者简介:郝振兴(1991—),男,河北唐山人,硕士研究生,研究方向:航空指挥控制与战术导引。E-mail:879070141@qq.com。
*收稿日期:2015-08-21
