基于分数阶傅里叶变换的高动态目标检测方法

黄明军，王永民，牛家红

(空军工程大学信息与导航学院，陕西 西安 710077)



基于分数阶傅里叶变换的高动态目标检测方法

黄明军，王永民，牛家红

(空军工程大学信息与导航学院，陕西 西安 710077)

摘要:针对高动态环境下接收机的接收信号含有较大多普勒频率及其变化率，传统捕获方法无法对多普勒频率变化率进行有效补偿的问题，提出了基于分段自相关分数阶傅里叶变换的高动态目标检测方法。该方法首先对接收信号进行载频预测，将接收信号调制到基带信号，然后利用分数阶傅里叶变换对线性调频信号在最优阶次具有能量聚集的特点，采用分段自相关与离散分数阶傅里叶变换相结合的处理方法，快速而准确的估计出多普勒频率及其变化率。仿真验证表明，该方法解决了传统方法在高动态环境下难以对信号多普勒变化率进行有效补偿的问题，并提高了检测信噪比和接收机捕获概率。

关键词:高动态；捕获；线性调频；分数阶傅里叶变换；检测

0引言

直接序列扩频体制在测控、通信和导航等领域中有着广泛的应用，但扩频技术的广泛应用是以准确同步为前提的。航天测控中，由于飞行器离地面站较远，且飞行速度高，接收信号的能量微弱同时还具有较高的多普勒频率变化率，因而高动态环境下伪码快速捕获是实现飞行器测控的关键因素。

伪码捕获方法众多，当前多使用并行快速傅里叶变换(Fast Fourier Transform，FFT) 的方法进行捕获，它的一大优点是捕获速度快，如文献[1—3]所提出的方法。基于 FFT方法在频域进行捕获时，不仅会引起由于时域截断而产生的能量泄漏和分析点个数有限而带来的扇贝损失[4]，而且在高动态环境下由于载体高速运动使信号产生了较大多普勒频率，并伴有较大多普勒频率变化率，这些捕获方法难以对由加速度引起的多普勒频率变化率分量进行有效补偿[5]。因而，传统捕获方法在高动态环境下并不适用，尤其是对捕获准确性要求较高的场合下。针对此问题，本文在文献[6]的基础上，提出了一种基于分段自相关分数阶傅里叶变换的高动态目标检测方法。

1分数阶傅里叶变换技术

在卫星移动通信与深空测控通信等高动态环境下，由于载体的机动范围和机动强度很大，使得发射信号的多普勒频移、一次变化率、甚至二次变化率都比较大，使信号参数发生强烈变化。当多普勒频移达到±25 kHz时就对信号捕获时频域的搜索带宽提出了较高要求，频域带宽增加，使得频域搜索点个数增加，数据处理量增大[7]；另外，由于频率变化率的存在，使得载波频偏不再是一个恒定不变的常数，这就给伪码快速捕获带来了困难，使得传统捕获方法不再适用于高动态环境。

设在高动态环境下，载波频偏表示为fd(t)，将其进行泰勒级数展开，则表为:

(1)

由于频率变化率k的存在，导致多普勒频率不断变化，因此在一段观测时间内信号不能看作频率不变的信号，信号离散傅里叶变换频谱也不再是一个单峰谱，而是由高动态性引起的扩展频谱，离散傅里叶变换是不适用的。图 1中可以明显看到信号傅里叶变换频谱能量无法集中，不再出现单峰，而是出现频谱扩展现象，无法进行频偏估计。因此，高动态环境下，传统利用FFT估计频偏的效果并不理想。基于此，在高动态环境下，现阶段将分数阶傅里叶变化技术(FRFT)引入到了伪码捕获算法当中。

分数傅里叶变换理论是在传统傅里叶分析的基础上迅速发展起来的一门新兴学科。傅里叶变换的基函数是一族指数函数{ejwt}，因此，傅里叶变换适合分析平稳信号，对现实物理世界中的多数非平稳信号是不适用的。在时频平面中，时间轴与频率轴相互垂直，即认为傅里叶变换将信号从时间域旋转π/2变换到频率域。如果将时频平面旋转不是π/2的整数倍角度时，信号在这个域的表示则由分数阶傅里叶变换给出，这个域称为分数阶傅里叶变换域[8]。

根据文献[9]，信号s(t)在旋转角度α下的FRFT表示为：

(2)

其中，p是FRFT的阶数，p=2α/π，变换核

(3)

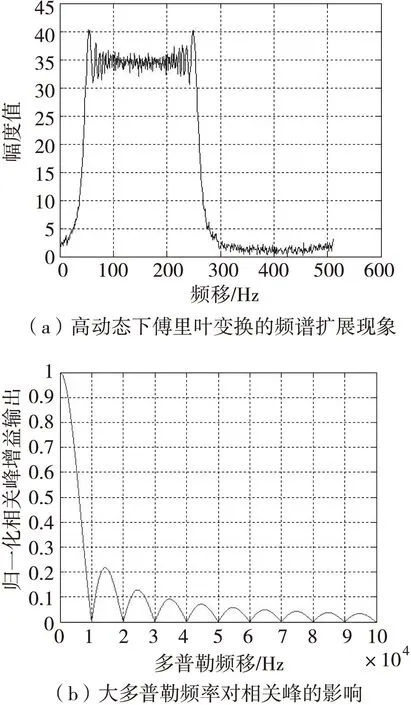
图1　高动态对捕获性能影响Fig.1　Capture high dynamic impact on performance graph

图2给出了Chirp信号的FT和FRFT示意图。Chirp信号在时频平面上呈斜刀刃状，具有明显的时频耦合特性。Chirp信号的FT可以看作是其在频率轴f上的投影，较宽的频谱使得能量分散；而FRFT则是在旋转角度α后u轴上的投影。随着旋转角度在[0,π]范围内变换，分数阶Fourier变换展示出信号从时域逐步变化到频域的所有变化特征，可以为信号时频分析提供更大选择余地；从物理意义上讲，FRFT就是将信号在时频平面的任意旋转。从上式可以看出，当旋转角度为0时，即是信号本身，旋转角度为π/2时信号FRFT变换就是其频域特征，合适的旋转角度α可以使Chirp信号的能量高度集聚，产生一个很窄的积累峰值，利于对信号的检测与估计，这一性质在对LFM信号的处理中具有很大优势。

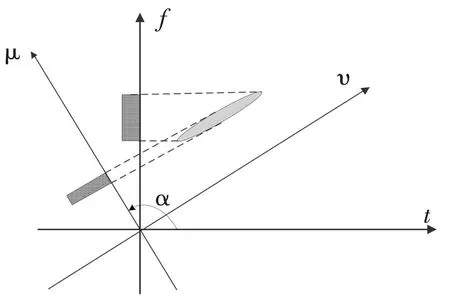
图2　LFM信号的Fourier变换与FRFT比较Fig.2　Compare Fourier transform and FRFT on LFM signal

2分段自相关FRFT的高动态目标检测原理

由1知，传统捕获方法无法检测出多普勒频率变化率的补偿量，因而不适合高动态环境下信号的快速捕获。基于此，本文提出了分段自相关与分数阶傅里叶变换相结合的高动态目标检测方法，有效估计了多普勒频率变化率。所提方法先通过FFT对信号载频预测，减小频偏变化区间，再通过部分匹配滤波器(PMF)近一步降低数据处理量，大大减小了捕获时间，最后利用FRFT对调频信号有能量聚积的特性，通过检测峰值来估计多普勒变化率分量。具体实现如图3所示。

图3　F-PMF-FRFT系统原理图Fig.3　Schematic of F-PMF-FRFT System

从系统的原理框图可以看出，本文所提算法主要包括三个步骤：第一，对接收到的中频信号分为I和Q路并分别相乘，对相乘后的信号进行FFT变换，预测多普勒频偏，然后进行混频，得到基带信号；第二步，对基带信号进行部分相关降采样，得到P个相关值；最后，对这P个相关值进行FRFT搜索，利用chirp信号在合适角度出现能量聚集的特性得到相关峰值并与门限值比较，估计出残余多普勒频偏fd′和频率变化率k。由此可见，该方法能够通过检测峰值估算出多普勒频移及其变化率分量，从而进一步实现伪码捕获。

设高动态下接收到的信号为：

(4)

由式(1)、式(4)得：

(5)

则混频后的零中频信号为：

(6)

假设伪码已经同步，则混频后的零中频信号为：

(7)

经过数字化采样后，可得

(8)

其中m=1,2,3,…,M-1，M为抽样后的点数。

每个单元信号可以表示为：

(9)

其中p=0,1,2,…,P-1,n=1,2,…,N-1。

分别对P个单元进行相干积累，得到的P个相干积累值为：

(10)

其中，B=A·exp(j(2πpNfd′/fs+πkp2N2/fs2+φ))

根据文献[10]中离散时间分数阶傅里叶变换的定义，序列x(n)可在p阶分数阶傅里叶域数字频率轴上表示为：

(11)

根据这种算法，离散信号关于alpha的N点DFRFT可表示为[11]：

(12)

联合式(10)、式(11)、式(12)得到

sk(α,m)=AαP-1/2·

p2cotα)/P]·A·

exp(j(2πpNfd′/fs+πkp2N2/fs2))·

2nfd′/fs+2kpNn/fs2]}·

p2(cotα/P+2kN2/fs2)]}

(13)

当-2mcscα/P+2Nfd′/fs=0,cotα/P+kN2/fs2=0时，sk(α,m)值最大，此时信号在分数阶傅里叶域具有最好能量聚集性，出现明显的峰值，通过对sk(α,m)在(α,m)平面做峰值搜索得到与LFM信号对应得峰值坐标(α,m)，基于此对信号频偏差和频率变化率进行估计。

(14)

3仿真验证及性能分析

为了分析上述算法在高动态环境下的捕获性能，本文采用观测时间Tp=4 s,扩频码长度为4096的扩频系统，输入均值为0、信噪比SNR=-20 dB的加性高斯白噪声，预测后的多普勒频偏差为100 Hz，多普勒频率变化率为100 Hz/s，fs=1 000 Hz,P=128，N=32的性能指标使用 MATLAB进行仿真，仿真结果如图4所示。

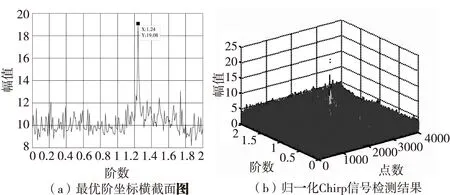
图4　F-PMF-FRFT系统仿真图Fig.4　Simulation diagram of F-PMF-FRFT system

由于Chirp 信号在相应阶次的分数阶傅里叶域内能实现能量聚集，高斯噪声在任何分数阶傅里叶变换域都呈现高斯形状，在分数阶傅里叶域上高斯噪声不具有很好的时频聚焦性，因而，图4出现了明显峰值，易于信号的检测与参数估计。由图4可以看出，峰值对应的二维平面坐标值为p0=1.24。由此可推得：实际信号的参数估计为k=98.98 Hz/s，fd=99.95 Hz。通过计算可得频率的估算误差为：(100-99.95)/100=0.05%，频率变化率的估算误差为：(100-98.98)/100=1.02% 。

通过仿真系统在不同信噪比时高动态目标参数估计、不同分数阶次步长Δp时高动态目标参数估计、不同分段匹配滤波器个数P时高动态目标参数估计得到表1-表3。

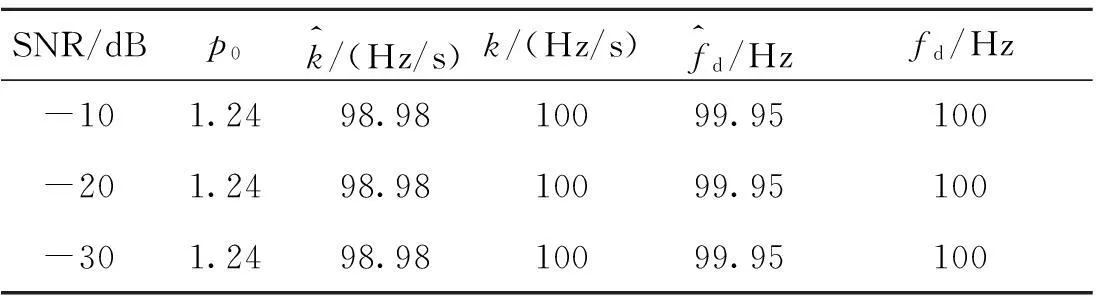
表1　不同信噪比时高动态目标参数估计

表1给出了分数阶次步长Δp=0.01，分段匹配滤波器个数P=128条件下，不同信噪比时高动态目标参数估计情况。由表1可知，当SNR为-10 dB、-20 dB和-30 dB时，由于目标峰值明显高于噪声，故其参数估计相同。

表2给出了SNR=-20 dB条件下，不同分数阶次步长Δp时高动态目标的参数估计情况，由表2可知，随着步长Δp的减小，参数估计精度越来越高。

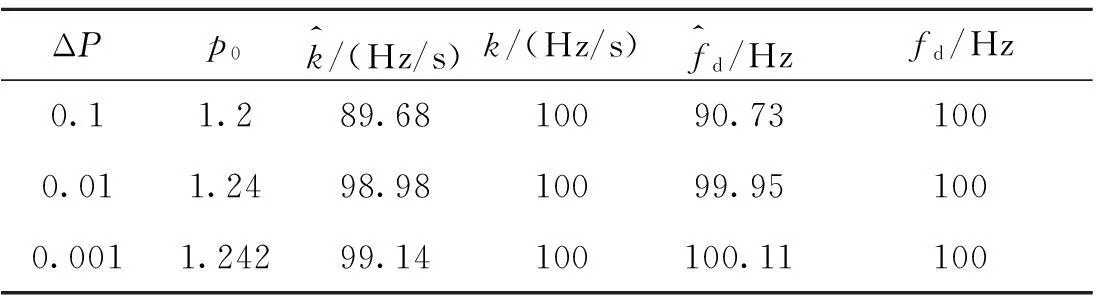
表2　不同分数阶次步长ΔP时高动态目标参数估计

表3给出了-20 dB条件下，不同分段匹配滤波器个数时高动态目标的参数估计情况，由表3可知，随着匹配滤波器个数P的增加，参数估计精度越来越高。

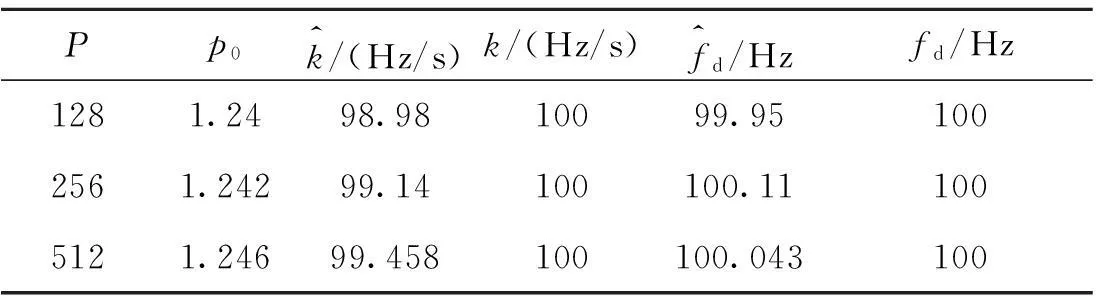
表3　不同分段匹配滤波器个数P时

4结论

在传统捕获算法的基础上，本文提出了分段自相关分数阶傅里叶变换的高动态目标检测方法。该方法提出先对接收信号进行FFT变换预测多普勒频率，然后采用PMF对信号进行降采样，之后再进行FRFT变换，通过检测信号峰值估算出多普勒频移及其变化率分量。理论分析和仿真结果表明，本文提出的方法解决了传统方法无法对频率变化率进行补偿的问题，也大大减少了FRFT算法计算量，缩短了捕获时间。同时，所提算法利用高斯白噪声在任意阶次的分数阶傅里叶域内能量分布是均匀的，在估计相关参数的同时抑制了噪声,提高了信号的检测信噪比，增强了系统抗噪性能，易于实现高动态环境下信号的快速捕获，在工程实践中具有一定的实用价值。

参考文献:

[1]AKOPIAN D． Fast FFT based GPS satellite acquisition methods[J]．IEEE Proceedings of Radar Sonar and Navigation, 2005, 154(4):277-286.

[2]CANDIDA L S, SASCHA M S, GORDON J R P,et al. A Serial parallel FFT correlator for PN code acquisition from LEO satellites[C] // International Symposium on Spread Spectrum Techniques and Applications. Washington, DC:IEEE, 1998

[3]黄烈超,张天骐,杜晓华.基于PMF-FFT的高动态多进制扩频信号的捕获算法[J].计算机应用研究,2011,28(9):3407-3410.

[4]章兰英,袁嗣杰,陈源. 航天扩频测控系统中伪码捕获方法研究[J]. 电子学报，2011，06(6):1471-1476.

[5]郇浩, 陶选如, 陶然,等. 多普勒频率变化率快速最大似然估计辅助的高动态载波跟踪环路[J].电子与信息学报，2014，36(3):577-582.

[6]房琪. 基于分数阶Fourier变换的LFM类信号的DOA估计[D].兰州：兰州交通大学，2013.

[7]陈斌杰,陈敏锋.高动态下GPS信号的捕获和跟踪技术研究[J]. 现代电子技 术,2006,218(3):13-15.

[8]于凤芹，曹家麟. 基于分数阶傅里叶变换的多分量chirp信号的检测与参数估计[J].电声技术，2004:53-59.

[9]战立晓,汤子跃,朱振波. 基于分数阶傅里叶变换的加速微弱目标检测与估计[J]. 电波科学学报,2013,28(2):296-304.

[10]Erseghe T, Kraniauskas P, Cariolaro G. Unified fractional Fourier transform and sampling theorem[J].IEEE Transactions on Signal Processing, 1999, 47(12): 3419-3423.

[11]陶然,周云松. 基于分数阶傅里叶变换的宽带LFM信号波达方向估计新算法[J]. 北京理工大学学报,2005,25(10):895-899.

High-Dynamic Target Detection Method Based on FRFT

HUANG Mingjun ，WANG Yongmin ，NIU Jiahong

(Information and Navigation College，Air Force Engineering University，Xi’an 710077，China)

Abstract:The received signal contained large Doppler frequency and its changing rate was high when the receiver in high dynamic environment, and traditional methods could not capture the changing rate of Doppler frequency for effective compensation. Aiming at this problem, a high dynamic target detection method based on fractional Fourier transform was proposed. This method first projected the receiving signals’ carrier frequency, Then using fractional Fourier transform of linear frequency modulation signal of the characteristics of energy in the optimal order times. The method of segmented autocorrelation combined discrete fractional Fourier transform to process the signal quickly and accurately. The theoretical analysis and simulation showed that this method could solve the problem that the traditional methods could not capture the changing rate of Doppler frequency for effective compensation, and improved the detection SNR and receiver’s capture probability.

Key words:high dynamic; capture; linear?frequency?modulation; fractional Fourier transform; detection

中图分类号:TN914

文献标志码:A

文章编号：1008-1194(2016)01-0037-05

作者简介:黄明军(1990—)，男，安徽舒城人，硕士研究生，研究方向：扩频通信、通信抗干扰。E-mail:513760454@qq.com。

基金项目:国家自然科学基金项目资助(61001111)

*收稿日期:2015-09-01