单加速度计高旋弹滚转角测量系统误差模型
2016-04-07徐国泰钱荣朝王佳伟
史 凯,徐国泰,钱荣朝,王佳伟
(西安机电信息技术研究所,陕西 西安 710065)
单加速度计高旋弹滚转角测量系统误差模型
史凯,徐国泰,钱荣朝,王佳伟
(西安机电信息技术研究所,陕西 西安 710065)
摘要:针对单加速度计高旋弹滚转角测量系统精度评估方法缺乏的问题,提出了单加速度计高旋弹滚转角测量系统误差模型。该模型中包含加速度计安装位置、安装角度、横轴灵敏度误差。分别用单因素敏感因子合成法和蒙特-卡洛模拟仿真法对单加速度计高旋弹滚转角测量精度的评估结果分别为3.577 2°和3.864 8°基本一致,仿真结果表明单加速度计高旋弹滚转角测量误差模型是正确的。
关键词:弹道修正;滚转角;加速度计;误差模型;精度评估
0引言
火力打击精确化是现代炮兵的重要标志,也是城市和复杂地形条件下新的作战模式对炮兵火力提出的新要求。然而,精确打击弹药成本太高,大量装备部队目前还不太现实。因而,常规兵器的制导化,制导武器的小型化成为未来武器系统的发展趋势。效费比高的灵巧弹药和智能弹药成为各国争相研究的热点,二维弹道修正引信技术正是在这样的背景下出现的[1]。对于二维弹道修正技术来说,高旋榴弹滚转角的测量是一个关键技术。
目前,国内外满足高过载、高动态、高精度的弹丸姿态测量方法有:MEMS陀螺方式、加速度计和磁强计组合方式、多加速度计组合方式[2]、磁强计和太阳方位角传感器组合方式[3]。其中MEMS陀螺方式滚转角测量不适用于高旋榴弹;而加速度计和磁强计组合方式由于安装在刚体弹丸内部,抗干扰能力差,易受铁磁干扰;多加速度计组合方式由于离心加速度导致的轴向加速度输出远大于弹丸轴向加速度工程化有难度;磁强计和太阳方位角传感器组合方式对天气依赖性较大,其中文献[4]介绍了一种单加速度计滚转角测量方法[4],但对其具体细节未进行报道,文献[5]进一步研究了单加速度计滚转角测量方法,揭示了基于科氏加速度的测量原理[5],但并未对系统测量精度进行评估。本文针对此问题,提出了单加速度计高旋弹滚转角测量系统误差模型。
1测量原理
在引信内部,将一个加速度计安置于距离弹轴r处,并且使加速度计的敏感轴方向与弹轴平行,如图1所示。由于弹丸存在高速自转,造成加速度计所在位置相对于准弹体坐标系(动坐标系)存在垂直于x轴的速度。这样由于准弹体系本身具有俯仰角速度,而加速度计所在位置与准弹体坐标系存在相对运动,则会产生一个牵连的科氏加速度[5]。

图1 单加速度计滚转角测量原理图Fig.1 Principle diagram of Single accelerometer roll angle measuring
通过上述分析可知科氏加速度是正弦的,而科氏加速度的相位与滚转角是一一对应的,该科氏加速度用ak表示,加速度计所在位置相对准弹体坐标系的速度用νa来表示,弹丸滚转角速度用ωspin表示,弹丸俯仰角速度即准弹体坐标系的俯仰角速度用ωpitch over表示,加速度计与弹轴距离用r表示,这样加速度计敏感到的科氏加速度ak如式(1)所示:
ak=2·ωpitchover×(ωspin×r)
(1)
由于科氏加速度自身是不能直接通过加速度计输出得到的,首先得到的是加速度计实际输出信号,对于加速度计输出信号进行实时信号处理才能得到科氏加速度,在理想情况下得到加速度计的实际输出信号以后,需要进行数字滤波器设计,确保滤波后信号相位基本保持不变,在得到科氏加速度以后需要设计锁相环锁定科氏加速度信号相位,最终确定滚转角,图2、图3分别为加速度计输出信号和科氏加速度信号。

图2 理论加速度计输出信号Fig.2 Theory signal of the accelerometer output
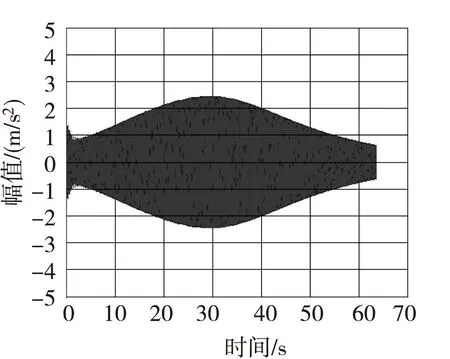
图3 滤波后得到的信号即科氏加速度Fig.3 Coriolis acceleration signal after filtering
2系统误差模型
2.1误差模型
加速度计在弹体坐标系下安装位置误差用Δx、Δy、Δz表示,安装方向的两个角度误差为α、β表示,横轴灵敏度误差用ξ表示,设弹丸角速度为(ωx、ωy、ωz),加速度计输出为(αpx、αpy、αpz)。为了准确分析出影响滚转角测量误差的内部原因,在分析加速度计误差过程中不考虑弹丸飞行过程中攻角所带来的影响,基于弹箭外弹道理论,可以推导出轴向加速度传感器引入误差后的输出模型,其中包含了安装位置引起的误差f(Δx,Δy,Δz)、传感器的安装角度引起的误差f(α,β)、传感器的横轴灵敏度引起的误差f(ξ)。
(2)
从式(2)中可以看出安装位置误差主要与弹丸的滚转角速度有关,而加速度计安装角度误差主要跟径向传感器输出有关,这是因为由于安装角度会导致径向传感器输出有分量投影到轴向传感器输出,横轴灵敏度显而易见主要跟加速度计的径向输出有关。
由于锁相环与滤波器带来的滚转角测量误差受硬件限制,故本文建立的滚转角误差模型,主要引入了加速度传感器安装误差(包括安装位置误差、安装角度误差)以及加速度传感器的横轴灵敏度、零位漂移等因素的影响。这些误差源中,加速度传感器的安装位置误差可以通过滤波方法消除,对于加速度传感器的横轴灵敏度、零位漂移等加速度传感器本身的不理想性,以及安装方向误差可通过实验室标定或者其他标定方法来消除。
2.2轴向加速度计输出推导
下面通过公式推导轴向加速度传感器引入误差后的输出。
传感器引入误差后的输出框图如图4所示。

图4 加速度传感器的输出框图Fig.4 Output of the acceleration sensor block diagram
由于加速度传感器的零位漂移是一个随机量,本文所用到的科氏加速度信号是加速度计实际输出信号经过带通滤波器将直流分量滤波后的周期信号,故加速度传感器的零位漂移在仿真计算过程中可以忽略。
设在固连坐标系中,弹丸的速度矢量V和角速度ω分别表示为:
(3)
加速度传感器的理想安装位置为弹丸质心位置,且敏感方向与弹轴方向一致,然而由于加速度传感器安装在引信上,引信不可能安装在弹丸质心,因此实际应用上加速度传感器在安装后肯定存在安装误差。设传感器安装在引信上,引信安装在弹体上后,传感器敏感单元实际位置为:p=(Δx,Δy,Δz)。
则P处加速度传感器引入位置误差后的输出值为:
(4)
其中:A为固连坐标系到地面坐标系的坐标转换矩阵。
当加速度传感器的敏感方向为XP与固连坐标系的横轴不重合时,该加速度传感器敏感方向在固连坐标系上的矢量如图5所示。
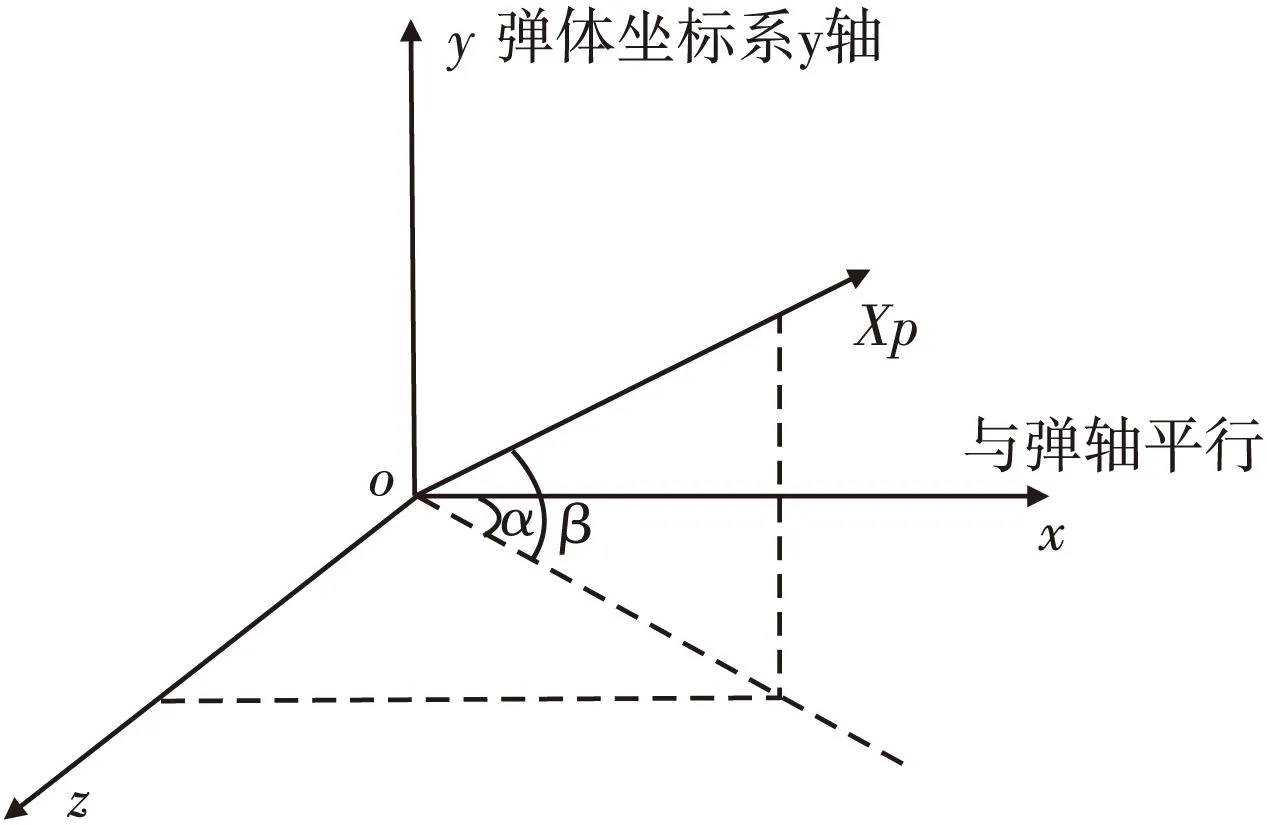
图5 固连坐标系到传感器坐标系之间的位置关系Fig.5 Location of the relationship between fixed coordinate system and the sensor coordinate system
由上图可以看出,固连坐标系到芯片坐标系之间(加速度传感器敏感轴所在的坐标系)的坐标转换矩阵:
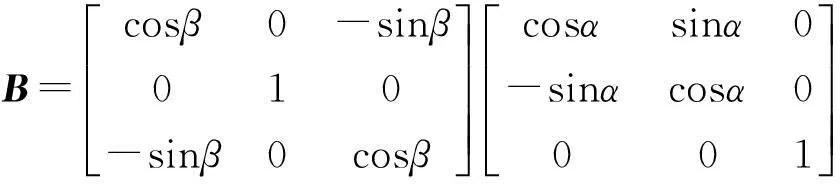
由弹丸外弹道理论可知,质心绝对加速度在固连坐标系OXYZ各坐标轴上的投影为:
(5)
引入位置误差p=(Δx,Δy,Δz)处P点的绝对加速度在固连坐标系OXYZ各坐标轴的投影为:
(6)
由于加速度传感器是以比力的形式输出的,因此固连坐标系下引入安装位置误差p后加速度传感器的理论输出为:
(7)
引入传感器角度误差后在固连坐标系下加速度传感器的理论输出为:
(8)

(9)
展开式(9),则引入加速度计安装位置误差、安装角度误差、横轴灵敏度误差后加速度传感器实际输出模型如式(10)所示。
cosβcosα·apx+cosβsinα·apy-
cosβsinα·apy-sinβ·apz+
(10)
3精度评估
得到单加速度计滚转角测量系统误差模型后,本章分别用单因素敏感因子合成法和1000次蒙特-卡洛模拟仿真方法对单加速度计滚转角测量精度进行评估。
3.1单因素敏感因子合成法精度评估
影响滚转角测量精度的误差主要包括安装位置、安装方向及传感器的横轴轴灵敏度等。采用单因素变化法计算各误差的敏感因子,由影响滚转角测量精度的各个因素的敏感因子和概率误差,计算出滚转角的测量精度。
引入各项误差取值模型为正态分布N(0,σ2),仅引入X轴测量误差,误差分别从-10~10 mm每隔1 mm取值,评估滚转角测量精度,然后通过曲线拟合可以得出仅引入X轴误差情况下的敏感因子,同理可以得出各项敏感因子数值。
采用公式(9)作为传感器理论输出模型;线性数字相位滤波器的通带为150~250Hz;锁相环锁定相位;加速度传感器理论安装位置为(500mm,25.4mm,0mm),各项敏感因子数值如表1所示。

表1 各项敏感因子数值
从表中可以看出安装位置对滚转角测量的误差影响较小,安装误差角度对滚转角测量的误差影响很大,每1°安装角度误差会带来0.585 6°的滚转角解算误差。
根据硬件结构的设计及加工经验,选取了加速度计三个轴向安装位置误差均为3mm,安装方向角度误差取5°,根据加速度计器件手册选取横轴灵敏度5%,采用单因素误差合成法计算滚转角测量误差,结果见表2。
3.2蒙特卡洛模拟法精度评估
以122mm榴弹为平台,采用蒙特-卡洛仿真法评估滚转角测量精度,评估方案见图6。6DOF外弹道模型仿真条件:全装药、43°射角、标准气象;加速度测量误差考虑了安装位置误差、安装角度误差、横轴灵敏度,取值见表2;滤波器选择为FIR线性数字带通滤波器,采样频率为10 000Hz,通带频率为150~250Hz;相位锁定通过锁相环仿真实现。

表2 单因素误差合成法滚转角测量精度计算
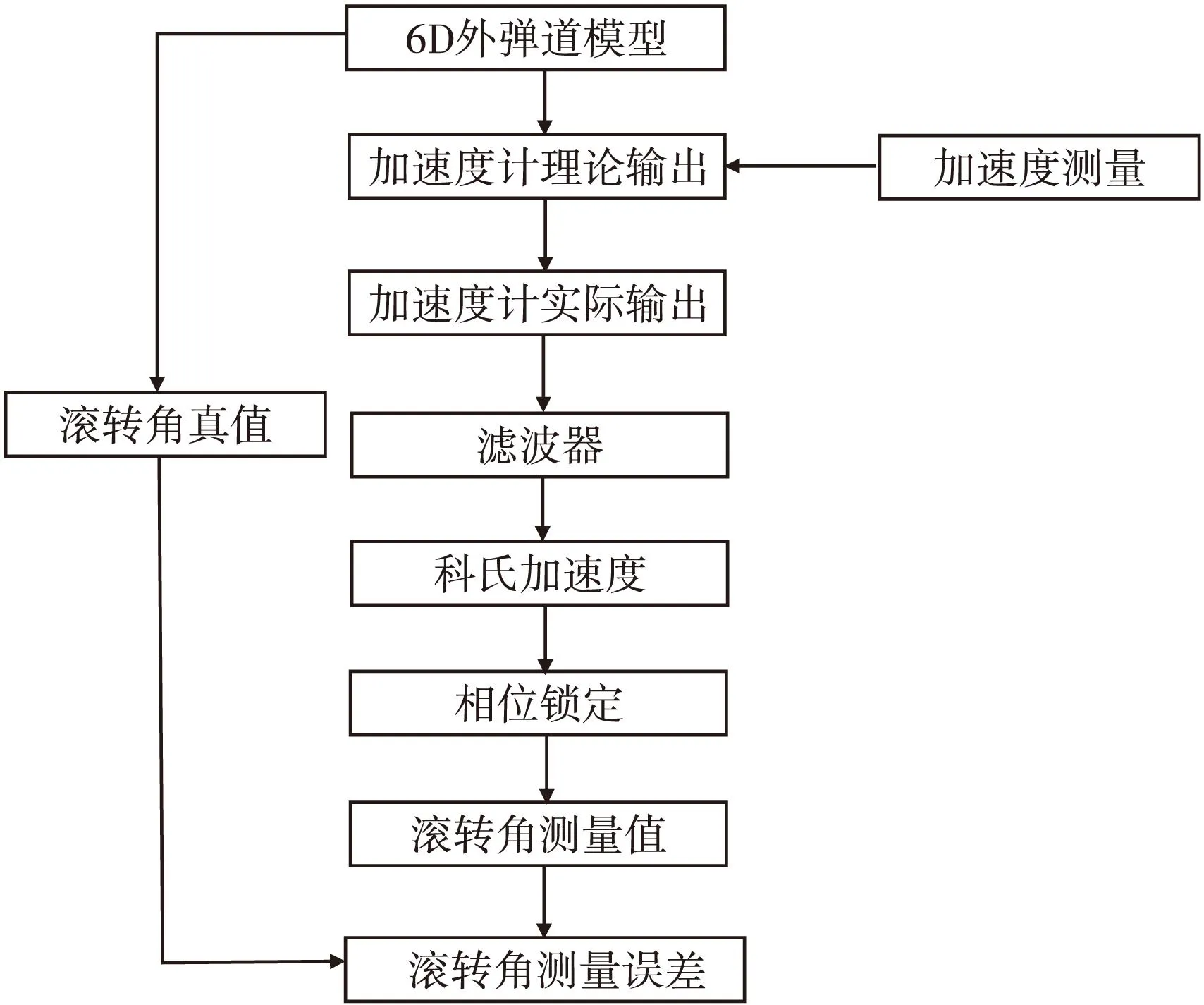
图6 滚转角测量流程图Fig.6 The flow chart of roll Angle measurement
采用与单因素敏感因子合成法相同的误差进行1000次蒙特-卡洛模拟仿真,仿真选取的影响滚转角测量精度各因素误差取值及仿真统计结果见表3。

表3 1 000次蒙特-卡洛模拟仿真法滚转角测量误差计算
由表2和表3可以看出,在影响滚转角测量精度各因素误差相同的条件下,单因素敏感因子合成法与蒙特-卡洛模拟仿真法计算的滚转角测量误差基本一致,结果如表4。

表4 两种测量方法结果
通过对比可以看出,两种评估方法得到的滚转角测量误差分别为3.577 2°和3.864 8°,都在4°以内,从而验证了单加速度计滚转角测量误差模型的正确性。
4结论
本文提出了单加速度计高旋弹滚转角测量误差模型。该模型中引入了传感器安装位置误差、安装角度误差以及加速度计横轴灵敏度,分别利用单因素敏感因子合成法与蒙特-卡洛模拟仿真法对测量精度进行了评估,仿真表明:单因素敏感因子合成法和蒙特-卡洛模拟仿真法计算出来的单加速度计滚转角测量误差分别为3.577 2°和3.864 8°,都在4°以内,证明了单加速度计高旋弹滚转角测量误差模型是正确的。
参考文献:
[1]范宁军.二维弹道修正引信总体方案和关键技术分析[J].战术导弹技术,2006,9(6):67-70.
[2]WilsonMichaelJ.AttitudeDeterminationWithMagnetometersforGun-LaunchedMunitions:US,7341221[P].2005-7-28.
[3]桂延宁.基于太阳方位角原理的炮弹飞行姿态遥测[J].兵工学报,2003,24(2):250-252.
[4]KreichaufRuth,LindquistErik.EstimationoftheRollAngleinaSpinningGuidedMunitionshell[C]//Position,Location,andNavigationSymposiam,IEEE, 2006:1-5.
[5]史凯,霍鹏飞,祁克玉.基于科氏加速度的旋转弹滚转角测量方法[J].探测与控制学报,2013,35(3):46-50.
Single Accelerometer Roll Angle Measurement System Error Analysis
SHI Kai, XU Guotai, QIAN Rongzhao, WANG Jiawei
(Xi’an Institute of Electromechanical Information Technology, Xi’an 710065,China)
Abstract:In order to study the single accelerometer high spinning projectile roll angle measurement system error and improve the accuracy of measurement, a single accelerometer roll angle measurement error model in high spinning projectile was established. The model contained the error of accelerometer installation location, installation angle and cross axis sensitivity. Respectively using single factor sensitive factor synthesis method and Monte Carlo simulation method to assess the accuracy of single accelerometer roll angle measurement in high spinning projectile, the two methods about the accuracy results was between 3.5772°and 3.8648°, so as to verified the correctness of single accelerometer roll angle measurement error model.
Key words:ballistic correction; roll angle; accelerometer; error model; precision evaluation
中图分类号:TJ765.4
文献标志码:A
文章编号:1008-1194(2016)01-0061-05
作者简介:史凯(1987—),男,陕西西安人,硕士,研究方向:弹道修正技术。E-mail:sky20041130@163.com。
*收稿日期:2015-08-26
