天地一体自主导航系统卫星广播星历参数拟合

陈刘成，徐　波

(1.南京大学 天文与空间科学学院，南京　210016；2.北京卫星导航工程中心，北京　100094)



天地一体自主导航系统卫星广播星历参数拟合

陈刘成1，2，徐波1

(1.南京大学 天文与空间科学学院，南京210016；2.北京卫星导航工程中心，北京100094)

摘要：本文针对现役卫星导航系统广播星历拟合及用户计算算法不能适用未来天地一体自主卫星导航系统的问题，提出利用切比雪夫多项式统一拟合多类型卫星轨道广播星历。利用BDS实际精密轨道数据和仿真拉格朗日平动点轨道数据试验表明，切比雪夫多项式星历拟合算法稳定可靠，灵活可控，计算量少，适用于所有类型导航卫星星载自主拟合。

关键词：卫星导航；拉格朗日平动点；广播星历；切比雪夫多项式

0引言

全球卫星导航系统(global navigation satellite system，GNSS)已经成为深刻改变人类社会及个人行为方式的航天工程，但目前只能满足近地空间和地球表面的导航需求。随着人类探索、利用太空的需求和能力的不断发展，支持中高轨、深空航天器导航制导，已经成为下一代卫星导航系统工程的重大需求。法库尔(Farquhar)在1967年提出了利用地月系拉格朗日平动点卫星支持月球深空导航后，文献[1-3]对此问题进行了深入的研究。文献[1-2]提出利用地月系拉格朗日平动点卫星星间链路观测量，自主实现卫星轨道的完全确定(Liaison导航技术)，此项技术已被用于构建下一代天地一体的卫星导航系统。文献[3]对构建天地一体卫星导航系统的系统架构、星座设计、力学模型、使用效能等进行了系统设计：由近地导航星座和地月系拉格朗日导航星座(L1、L2、L4、L5)构成整体运行星座，形成对深空用户的导航服务能力。

卫星导航系统广播星历是系统向用户实时广播的、用以表示卫星精确运动状态的一组参数，基本要求包括：用户计算量不能过大、仅需星历和接收机预存无需更新的常量信息就能准确预报卫星状态、星历表达地固坐标系运动状态。对于自主运行系统言，广播星历参数拟合还要求拟合算法简单可靠、计算量小[4]，算法适应星载计算环境。天地一体卫星导航系统涉及近地中圆地球轨道(medium Earth orbit，MEO)卫星、高轨倾斜轨道同步(inclined geosynchronous satellite orbit，IGSO)卫星、地球静止轨道(geostationary Earth orbit，GEO)卫星、拉格朗日平动点轨道卫星等多类型卫星。目前卫星广播星历参数拟合表达方法主要有开普勒轨道根数法[5-6]、状态矢量积分法[7]、多项式拟合方法[8-10]。总体而言，美国全球定位系统(global positioning system，GPS)开普勒轨道根数法拟合MEO导航卫星星历，用户使用方便、星历表达精度高、参数物理意义相对明确、参数取值范围可控便于工程接口设计[11]，被多数现役系统采用。但GPS开普勒轨道根数法对高轨卫星，特别是GEO卫星星历参数拟合的适用性并不好，这已对采用混合星座的区域卫星导航系统带来很多问题。文献[11-18]对此问题进行了广泛而深入的研究，认为高轨导航卫星的小偏心率、小倾角、J2，2项“共振效应”会带来星历参数拟合时法方程奇异、参数相关性奇高、拟合精度不高或不收敛、参数物理意义缺失、参数取值范围过大造成接口难以准确表达等问题，需要通过变换星历拟合坐标系参考平面、采用无奇点轨道根数、固定部分参数、采用参数加权的Givens变换解方程、采用带参数模约束的岭估计、动态加权的带参数约束条件平差算法、优化拟合初值选取、改变星历拟合弧长等方法来提升GPS开普勒轨道根数星历拟合方法对高轨导航卫星的适用性。拉格朗日平动点轨道限制性三体动力学特性完全不同于近地导航卫星的二体受摄运动，GPS开普勒轨道根数星历拟合方法已完全不能适用。为此，本文提出基于切比雪夫多项式的星历拟合方法，解决未来天地一体卫星导航系统广播星历的模型和算法统一的问题。

1切比雪夫拟合星历拟合及用户算法

用切比雪夫多项式拟合导航卫星广播星历本质上是拟合卫星运动轨迹，可以较好地适应各种类型的卫星轨道。相对于其他常用星历拟合算法，对运动速度慢和受摄均匀的卫星轨道，星历表达更为可靠、高效和精确[9]；相对于其他多项式拟合算法，不会出现龙格现象，即不会在拟合弧段两端产生精度的较大波动[8]。

1.1星历拟合算法

假设需要拟合轨道起止时间为[t0,t0+Δt]， 计算n阶切比雪夫多项式系数。其中t0为拟合弧段起点，Δt为拟合弧长。首先利用式(1)进行参数归一化变换。

(1)

则卫星坐标X、Y、Z的切比雪夫多项式为

(2)

式(2)中，n为切比雪夫多项式的阶数；CXi,CYi,CZi为三个位置分量的切比雪夫多项式拟合结果系数；Ti由式(3)确定为

T0(τ)=1,T1(τ)=τ,Tn(τ)=2τTn-1(τ)-Tn-2(τ)

(3)

星历拟合误差方程为

(4)

用最小二乘方法可求解上述方程[8-10]，可得最终广播星历参数：t0,CXi,CYi,CZi。

1.2用户使用算法

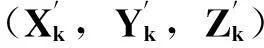
(5)

(6)

2多类型导航卫星星历拟合实验

采用实际近地GNSS系统精密轨道数据和动力学方法仿真的拉格朗日卫星轨道数据进行拟合实验。近地导航星座以北斗系统(BeiDou satellite navigation system，BDS)为例(包括MEO/IGSO/GEO)，拉格朗日导航星座包括L1、L2、L4、L5平动点卫星。仿真考虑摄动力包括地球引力，12×12地球重力场模型、日月引力、行星引力、太阳光压，采用IAU1976岁差和IAU1980章动模型。

星历拟合的弧长主要取决于算法稳定性、结果精确性、广播星历更新周期几个因素。从用户角度看，星历拟合的弧长必须大于等于星历更新周期。由文献[5，19]可知，目前不同卫星导航系统星历更新周期从30 min到2 h不等，本文取星历拟合长度为最大值2 h可能少的通信总量[11，20]，本文以最少的切比雪夫多项式阶数拟合dm级位置精度广播星历。

2.1MEO导航卫星星历拟合实验

根据BDS 2013-06-01实际卫星精密轨道数据，进行4颗MEO(编号09～12)卫星的8阶切比雪夫多项式拟合星历拟合实验，其误差情况如图1所示。

图1　M09卫星8阶切比雪夫多项式星历拟合误差

4颗MEO卫星8阶切比雪夫多项式星历参数拟合精度统计如表1所示：

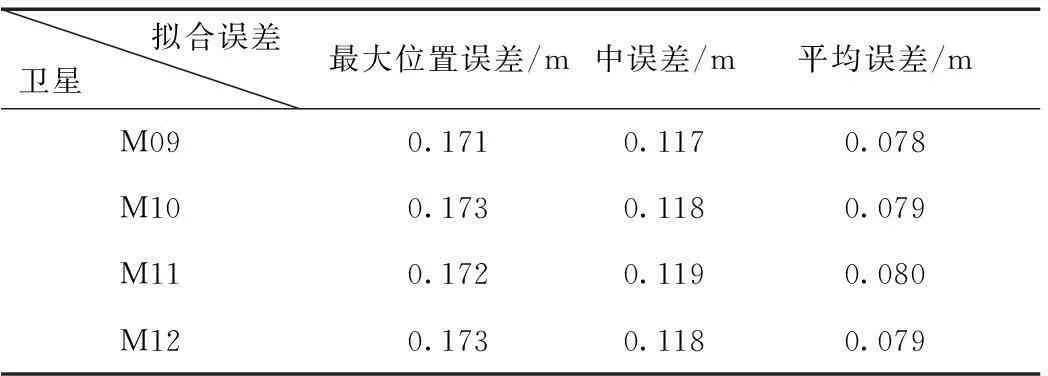
表1　MEO卫星8阶切比雪夫多项式拟合星历误差统计表

备注：拟合弧长2 h，累积拟合弧长24 h。

2.2IGSO导航卫星星历拟合实验

根据BDS 2013-06-01实际卫星精密轨道数据，进行3颗IGSO(编号06～08)卫星的7阶切比雪夫多项式拟合星历拟合实验，其误差情况如图2所示。

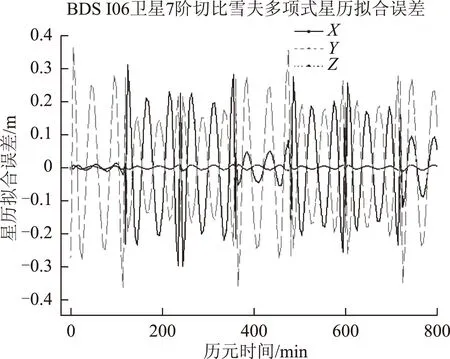
图2　IGSO卫星7阶切比雪夫多项式星历拟合误差

3颗IGSO卫星7阶切比雪夫多项式星历参数拟合精度统计如表2所示。

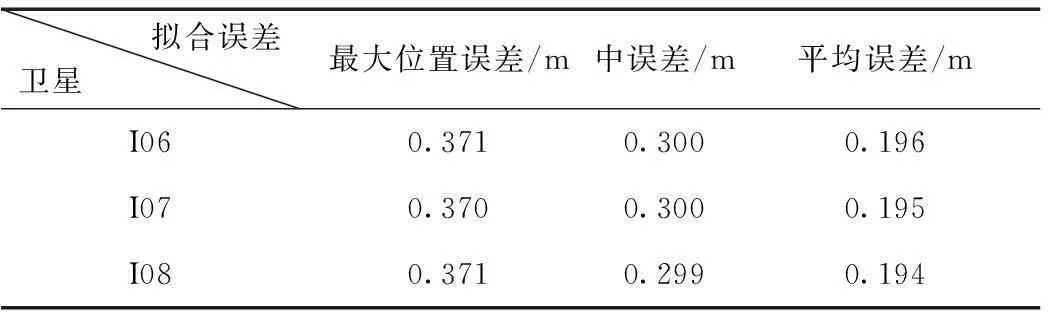
表2　IGSO卫星7阶切比雪夫多项式拟合星历误差统计表

备注：拟合弧长2 h，累积拟合弧长24 h。

2.3GEO导航卫星星历拟合实验

根据BDS 2013-06-01实际卫星精密轨道数据，进行5颗GEO(编号01～05)卫星的5阶切比雪夫多项式拟合星历拟合实验，其误差情况如图3所示。

图3　GEO卫星5阶切比雪夫多项式星历拟合误差

5颗GEO卫星5阶切比雪夫多项式星历参数拟合精度统计如表3所示：

表3　GEO卫星5阶切比雪夫多项式拟合星历误差统计表

备注：拟合弧长2 h，累积拟合弧长24 h。

2.4拉格朗日导航卫星星历拟合实验

仿真天地一体卫星导航系统2013-06-01 L01、L02、L04、L05共4颗地月系拉格朗日导航卫星动力学轨道，进行7阶切比雪夫多项式拟合星历的误差情况如图4所示。

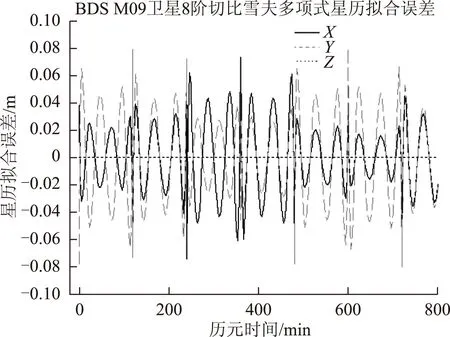
图4　地月系L01点拉格朗日导航星星历拟合误差

地月系L01、L02、L04、L05四颗拉格朗日平动点导航卫星7阶切比雪夫多项式星历拟合精度如表4所示。

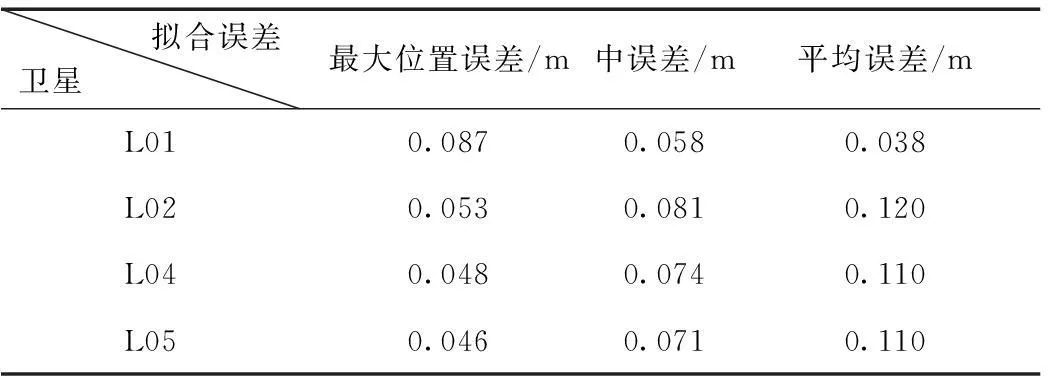
表4　地月系拉格朗日导航卫星7阶切比雪夫多项式

备注：拟合弧长2 h，累积拟合弧长24 h。

3结束语

(1)在相同切比雪夫多项式拟合阶数时，GEO卫星由于地固系内运动速度小(位置变化量小)、所受摄动力更为平滑，拟合精度相对较高；因此在相同的精度要求下，可由相对较少的拟合阶数满足星历拟合要求。MEO卫星由于运动速度大，所受摄动力变化相对剧烈，拟合精度相对稍差。

(2)采用切比雪夫多项式拟合天地一体卫星导航系统广播星历能够适应多种轨道类型卫星轨道，且拟合算法和用户算法简单可靠，计算量小，拟合精度满足要求。

参考文献

[1]HILL K A.Autonomous navigation in libration point orbits[D].Greeley：Graduate School of the University of Colorado，2007：24-27.

[2]WOLF R.Satellite orbit and ephemeris determination using inter satellite links[D].München：Universität der Bundeswehr，2000：51-62.

[3]ZHANG Lei，XU Bo.A universe light house-candidate architectures of the libration point satellite navigation system[J].Journal of Navigation，2014，67(5)：737-752.DOI：http：//dx.doi.org/10.1017/S0373463314000137.

[4]陈忠贵，刘光明，廖瑛，等.广播星历参数星上自主拟合算法[J].国防科技大学学报，2011，33(3)：1-5.

[5]黄华.导航卫星广播星历参数模型及拟合算法研究[D].南京：南京大学，2012：27-36.

[6]黄勇，胡小工，王小亚，等.中高轨卫星广播星历精度分析[J].天文学进展，2006，24(1)：81-88.

[7]陈刘成，韩春好，唐波.GLONASS卫星位置的动力学改进算法[J].测绘科学，2007，32(4)：8-10.

[8]杨永林，苟长龙，胡波.广播星历与精密星历切比雪夫插值的比较[J].测绘工程，2010，19(2)：10-14.

[9]陈刘成，贾小林，莫中秋.用切比雪夫曲线拟合导航卫星广播星历[J].天文学进展，2006，24 (2)：167-173.

[10]朱俊，文援兰，廖瑛.一种适用于各种轨道类型的导航卫星广播星历研究[J.航天控制，2005，23(6)：9-14.

[11]陈刘成，李静，马瑞，等.工程化广播星历参数拟合算法与接口设计[J].武汉大学学报·信息科学版，2011，36(1)：18-22.

[12]高玉东，郗哓宁，王威.GEO导航星广播星历拟合改进算法设计[J].国防科技大学学报，2007，29(5)：18-22.

[13]刘光明，廖瑛，文援兰.导航卫星广播星历参数拟合算法研究[J].国防科技大学学报，2008，30(3)：100-105.

[14]陈刘成，胡小工，常志巧，等.高轨导航卫星星历设计[J].中国科学：物理学 力学 天文学，2010，40(5)：608-615.

[15]陈刘成，韩春好，陈金平.广播星历参数拟合算法研究[J].测绘科学，2007，32(3)：12-16.

[16]崔先强.参数加权的Givens 变换算法及其在导航卫星广播星历拟合中的应用[J].大地测量与地球动力学，2010，30(3)：147-150.

[17]何峰，王刚，刘利，等.地球静止轨道卫星广播星历参数拟合与试验分析[J].测绘学报，2011，40(增刊)：52-56.

[18]韩星远，向开恒，王海红.第一类无奇点变量的广播星历参数拟合算法[J].航天器工程，2011，20(4)：54-57.

[19]黄文德，王威，郗哓宁.导航卫星广播星历误差特性频域分析及预报模型[J].中国空间科学技术，2010(3)：12-16.

[20]崔先强，陈南，贾小林.GPS星历参数比例因子的确定研究[J].全球定位系统，2007，32(2)：1-3.

The Broadcast Ephemeris Parameters Fitting for the Integrated Autonomous Navigation System of Space and Land

CHENLiucheng1，2，XUBo1

(1.School of Astronomy & Space Science in Nanjing university，Nanjing 210016，China；2.The Satellite Navigation Center of Beijing，Beijing 100094，China)

Abstract：To solve the problem that the ephemeris parameters fitting arithmetic of operational satellite navigations aren’t applicable for the integrated autonomous navigation system of space and land in the future，especially for the geostationary orbits and the Lagrange libration point orbits，the Chebyshev polynomial fitting algorithm is proposed to unify the multi-types satellites ephemeris parameters fitting.The fitting results，based on the operational COMPASS system satellite precise orbits and stimulated earth-moon system Lagrange libration point orbits，demonstrate that the Chebyshev polynomial is stable and reliable，flexible and controllable，with less calculation，and it is adapted to all-type satellite autonomous fitting onboard as well.

Key words：satellite navigation system；Lagrange libration point；the broadcast ephemeris parameters；Chebyshev polynomial

中图分类号：P228

文献标识码：A

文章编号：2095-4999(2016)-01-0094-04

作者简介：第一陈刘成(1977—)，男，江苏盐城人，高级工程师，博士，主要从事卫星导航相关技术研究。

基金项目：国家自然科学基金(41274043、41174026)。

收稿日期：2015-08-19

引文格式：陈刘成，徐波.天地一体自主导航系统卫星广播星历参数拟合[J].导航定位学报，2016，4(1)：94-97.(CHEN Liucheng，XU Bo.The Broadcast Ephemeris Parameters Fitting for the Integrated Autonomous Navigation System of Space and Land[J].Journal of Navigation and Positioning，2016，4(1)：94-97.)DOI：10.16547/j.cnki.10-1096.20160118.