精密单点定位收敛时间的确定方法研究

周承松，彭　月，张小红，刘文祥，王飞雪

(1.国防科技大学 电子科学与工程学院，长沙　410073；2.武汉大学 测绘学院，武汉　430079；

3.四川省测绘地理信息局，成都　610100)



精密单点定位收敛时间的确定方法研究

周承松1，彭月2，3，张小红2，刘文祥1，王飞雪1

(1.国防科技大学 电子科学与工程学院，长沙410073；2.武汉大学 测绘学院，武汉430079；

3.四川省测绘地理信息局，成都610100)

摘要：针对精密单点定位作业效率问题，本文基于精密单点定位结果时间序列的均值变化和方差变化提出了两种确定精密单点定位收敛时间的方法，并分别阐述了方法的原理。精密单点定位是将观测数据与相对应的卫星轨道、卫星钟差一并进行定位解算，得到定位结果时间序列。这种时间序列具有由非平稳逐渐收敛到平稳的特点，由非平稳到平稳所需的时间为精密单点定位收敛时间。工程应用中，由于缺少收敛时间的确定方法，精密单点定位的观测时间往往长于收敛时间，达到数个小时甚至更久，存在的冗余观测使得作业效率较低。本文根据大量实测数据对两种方法关于及时准确判断收敛时间方面的性能进行分析，结果表明两种方法均能判断收敛，均值变化法的收敛时间稍长于均值变化法；但两种方法确定的收敛时间大都在30 min级，不超过60 min。均值变化法能收敛到dm级和cm级；方差变化法能收敛到dm级，但会出现m级的定位偏差。

关键词：精密单点定位；时间序列；收敛时间；性能分析

0引言

自1997年美国喷气推进实验室的Zumbeger提出精密单点定位技术(precise point positioning，PPP)以来，PPP技术一直备受关注。相比于相对定位方式，PPP不需要基准站的支持，仅用单台接收机就可以获得高精度定位，流动性强，工作方式灵活[1]。随着高精度卫星轨道和钟差产品的发展，PPP在低轨卫星定轨、航空动态测量、海洋测绘、高精度坐标框架维持、精确授时等领域应用广泛[2-4]。

PPP是主要利用高精度的载波相位观测值以及高精度的卫星轨道和卫星钟差产品获取高精度定位结果，其中固定载波相位观测值的模糊度是PPP收敛的前提。模糊度固定需要分离模糊度的小数部分，再进行整数模糊度的搜索固定，单站模糊度的固定大都采用LAMBDA算法，其算法有两个过程：模糊度降相关处理和整数模糊度的搜索[5]。固定模糊度后，静态PPP可收敛到mm至cm级，动态PPP可收敛到cm至dm级；实时PPP可收敛到dm级至亚dm级，事后PPP可收敛到cm级至亚cm级[6]。由于固定模糊度需要一定时间，因此PPP定位结果呈现先浮动后收敛的特点，其收敛时间为定位结果序列由非平稳到平稳所需的时间[7]，然而随着用户对定位精度的要求不同，平稳的定义也不同，因此收敛时间是随定位精度而变化的[8]。在相同的定位精度要求下，PPP收敛时间受测站纬度、位置精度衰减因子(position dilution of precision,PDOP)值、卫星轨道、卫星钟差、信号传播误差、接收机有关误差和相对论效应等的影响[9]。由于模糊度不易固定，PPP收敛时间一般较长，一般需要0.5 h以上才能收敛到cm级[10]。在实际工程应用中，尤其是测绘领域，由于PPP收敛时间的确定技术尚不成熟，通常是约定俗成地延长观测时间来保证收敛，要达到cm级定位精度至少需要观测2 h，而一般情况下观测时间至少四个小时甚至更长，这对于作业效率是极不利的。例如，在静态PPP中，业界一般以最后一个观测历元的定位结果为PPP结果，如果该结果尚未收敛到相应的定位精度，除了返工重测别无他法；如果在最后一个历元之前就已收敛，则浪费了观测时间，可见研究收敛时间的确定方法是有必要的。

PPP收敛时间的确定方法的应用背景按时效性可分为实时PPP和事后PPP。实时PPP要求能获取实时精密星历和精密卫星钟差，那么收敛时间的及时确定可以大大减少观测时间；事后PPP需要获取事后精密星历和精密卫星钟差，另外由于事后PPP往往存在大量的冗余观测数据，那么收敛时间的及时确定能判定收敛，还能够避免计算机对冗余观测数据的解算，从而在一定程度上提高了作业效率。

目前，关于PPP收敛时间的确定方法的研究并不多见，尚未形成一套完整的理论系统。但判定时间序列平稳的文献较多，比较常见的判断方法有相邻数据差值、数据拟合等方法。但这两种方法都存在一定的局限性。相邻数据差值法，对于非平稳但变化缓慢的数据，这种方法会将其误判为平稳数据[11]；数据拟合法有多项式拟合或指数拟合，它们需要大量的定位结果数据进行拟合，所以只能应用于事后PPP，并且为了达到高精度拟合，多项式拟合需要进行高阶次拟合，易产生震荡现象[12]，而指数拟合往往会出现拟合发散的状况。利用均值和方差的变化情况来判定序列平稳不存在类似相邻数据差值、数据拟合等方法的缺陷，鉴于此，均值和方差的变化被广泛应用于时间序列变点估计领域[13]，本文利用均值和方差的变化情况，根据PPP定位结果时间序列中非平稳序列与平稳序列在均值和方差上的差异推导了两种收敛时间确定方法，并结合跟踪站参考坐标值对两种方法的性能进行实验分析与比较。

1PPP定位模型

1.1PPP观测方程

美国的全球定位系统(global positioning system，GPS)作为全球卫星导航系统(global navigation satellite system，GNSS)最先建成的导航定位系统，已经在各行各业中获得了广泛的应用。PPP的核心是对GPS单点定位中的卫星误差、传播过程误差、接收机误差进行分类处理：

1)利用精密卫星轨道和钟差校正卫星轨道误差和卫星钟差；

2)利用消电离层组合伪距和相位观测值进行定位解算，消除电离层延迟误差；

3)考虑GPS卫星天线相位中心改正、接收机天线相位中心改正、天线相位缠绕、测站固体潮、地球潮汐等改正；

4)将对流层延迟和接收机钟差与测站位置坐标一起作为未知参数进行定位解算。

目前PPP通常采用消电离层伪距和相位观测值(PIF和IIF)进行定位解算，其观测方程为

(1)

式(1)中，f1、 f2为以距离表示的相位观测值L1和L2的频率；P1、 P2为以距离表示的伪距观测值；ρ为卫星到接收机的几何距离；c为光速；λ1： 为相位观测值L1的波长；dT、 dt为接收机钟差和卫星钟差；Trop为对流层延迟；εP为包含多路径效应、卫星轨道误差等多种误差的消电离层伪距观测值噪声；εL为PPP包含多路径效应、卫星轨道误差等多种误差的消电离层相位观测值噪声；NIF为消电离层组合模糊度。

式(1)中的ρ和NIF记为

(2)

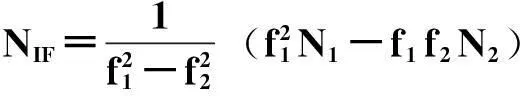
(3)

式(2)中，(XS,YS,ZS)为卫星坐标，(x,y,z)为接收机坐标。

1.2PPP参数估计

Xk=Φk,k-1Xk-1+ωk,ωk～N(0,Qk)

(4)

Zk=HkXk+Vk,Vk～N(0,Rk)

(5)

式(4)及式(5)中，Xk-1为k-1历元状态向量；Xk为k历元状态向量；Φk,k-1为 状态转移矩阵；ωk为 系统噪声向量；Zk为k历元观测值；Hk为 设计矩阵；Vk为 观测噪声向量；Qk为 系统噪声方差阵；Rk为 观测噪声方差阵。

Kalman滤波由预测和更新组成，具体步骤为

预测为

(6)

更新为

(7)

2确定 收敛时间的方法

上已叙及，PPP定位结果时间序列具有由非平稳逐渐收敛到平稳的特点[7]。确定PPP收敛时间，只需要判断该时间序列中非平稳部分和平稳部分的过渡点，定义该过渡点为时间序列收敛点。若判断出时间序列收敛点，根据该收敛点的观测历元就可得到PPP收敛时间。

非平稳序列的均值和方差波动较大，平稳序列的均值和方差波动相对较小[13]。因此，本文从均值和方差的角度判断出序列收敛点。将PPP定位结果时间序列按坐标轴x、 y、 z三个方向拆分成三个时间序列，分别进行收敛讨论。以x方向为例，对PPP收敛时间的确定方法进行简介。

2.1均值变化法

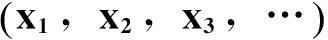
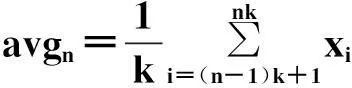
(8)

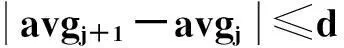
(9)

收敛点：x(j-1)k+1

收敛时间：T=[(j-1)k+1]·t

(10)

(11)

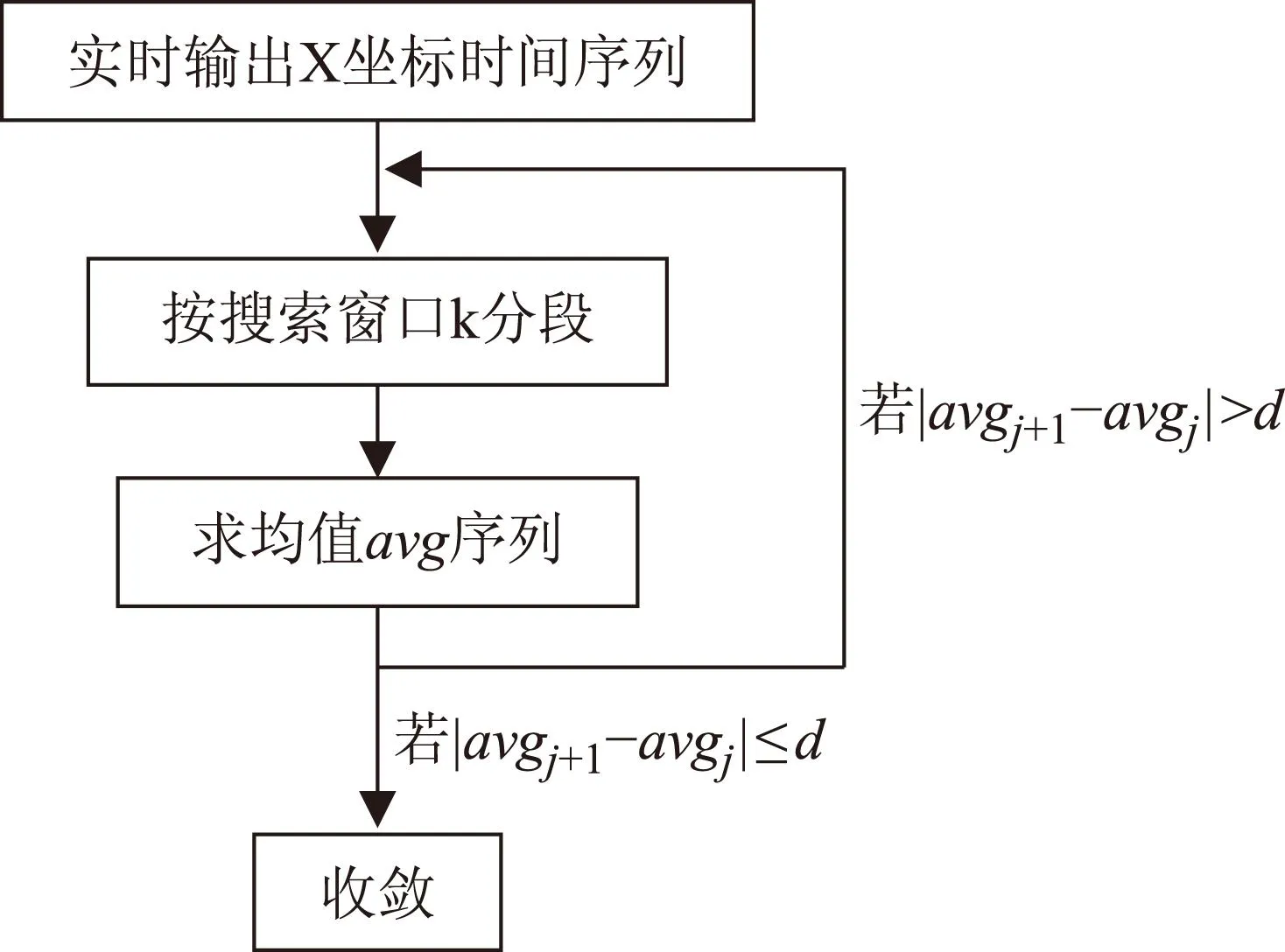
图1　均值变化法流程图

2.2方差变化法

方差变化法和均值变化法类似，只不过是从方差变化情况来判断时间序列平稳。现将与均值变化法不同的地方予以说明：

2.3阈值和搜索窗口的确定

均值变化法、方差变化法均需要确定合适的阈值d和搜索窗口k，才能准确判断PPP收敛。搜索窗口和阈值是根据PPP定位精度需求和收敛时间要求而确定的。在同一定位过程中，定位精度需求越高，则阈值应越小，搜索窗口应越长；相反，收敛时间越短，则阈值应越大，搜索窗口应越短。在实际应用中，是需要同时考虑定位精度和收敛时间的，一般根据经验值来确定阈值和搜索窗口，以满足用户需求。

本文实验中，为了获取阈值和搜索窗口的经验值，均值变化法在亚mm级、mm级、cm级和dm级均设有阈值，同时为了比较，方差变化法的阈值设为相应均值变化法阈值的平方，例如均值变化法阈值d=0.1 mm(即10-4m)，则相应的方差变化法阈值d′=10-8m2。另外，两种方法的搜索窗口长度均设为5历元、10历元、12历元、14历元、16历元、18历元、20历元和30历元。

3实验与分析

实验利用国际GNSS服务(international GNSS service，IGS)事后精密卫星星历和钟差对全球10个IGS跟踪站2015-08-20的观测数据进行定位解算，并根据均值变化法和方差变化法实时地确定定位结果时间序列的收敛时间，通过改变搜索窗口k和阈值d，得到各跟踪站在不同k和d下的收敛坐标，分别与IGS周解snx文件中各跟踪站坐标精确值进行对比，分析k和d对收敛结果的影响，并根据实验结果确定k、d的最优组合，进而用5个全球跟踪站2014-01-02～2015-01-02的一年观测数据对最优组合进行验证。与此同时，根据实验结果对两种方法关于收敛时间判断的准确性进行比较。需要说明的是，实时PPP的收敛时间确定方法和本实验中事后PPP收敛时间确定方法类似，只是其精密星历和精密钟差是实时的，故本实验只分析事后PPP收敛时间的确定方法。

3.1实验结果

实验数据为10个全球跟踪站2015-08-20的全天观测数据和相应的精密星历、精密钟差，每个跟踪站全天共2 880个观测历元(采样间隔为 30 s)。

采用扩展卡尔曼滤波(extended Kalman filter,EKF)滤波方法对实验数据进行消电离层组合定位解算，在不同搜索窗口和阈值下，利用两种方法确定10个跟踪站定位结果时间序列的收敛时间。根据2.3中阈值和搜索窗口的确定方法，在均值变化法中，阈值d=(0.1 mm，0.2 mm，1 mm，2 mm，1cm，2 cm，1 dm，2 dm)，搜索窗口在采样间隔为30 s情况下，设k=(2.5 min，5 min，6 min，7 min，8 min，9 min，10 min，15 min)；对应地，在方差变化法中，阈值d=(10-8m2，4×10-8m2，10-6m2，4×10-6m2，10-4m2，4×10-4m2，10-2m2，4×10-2m2)，搜索窗口与均值变化法相同。以adis跟踪站为例，在d=2 mm、k=5 min的情况下，其定位结果时间序列的收敛判断图如图2-3，图中“o”代表序列收敛点。

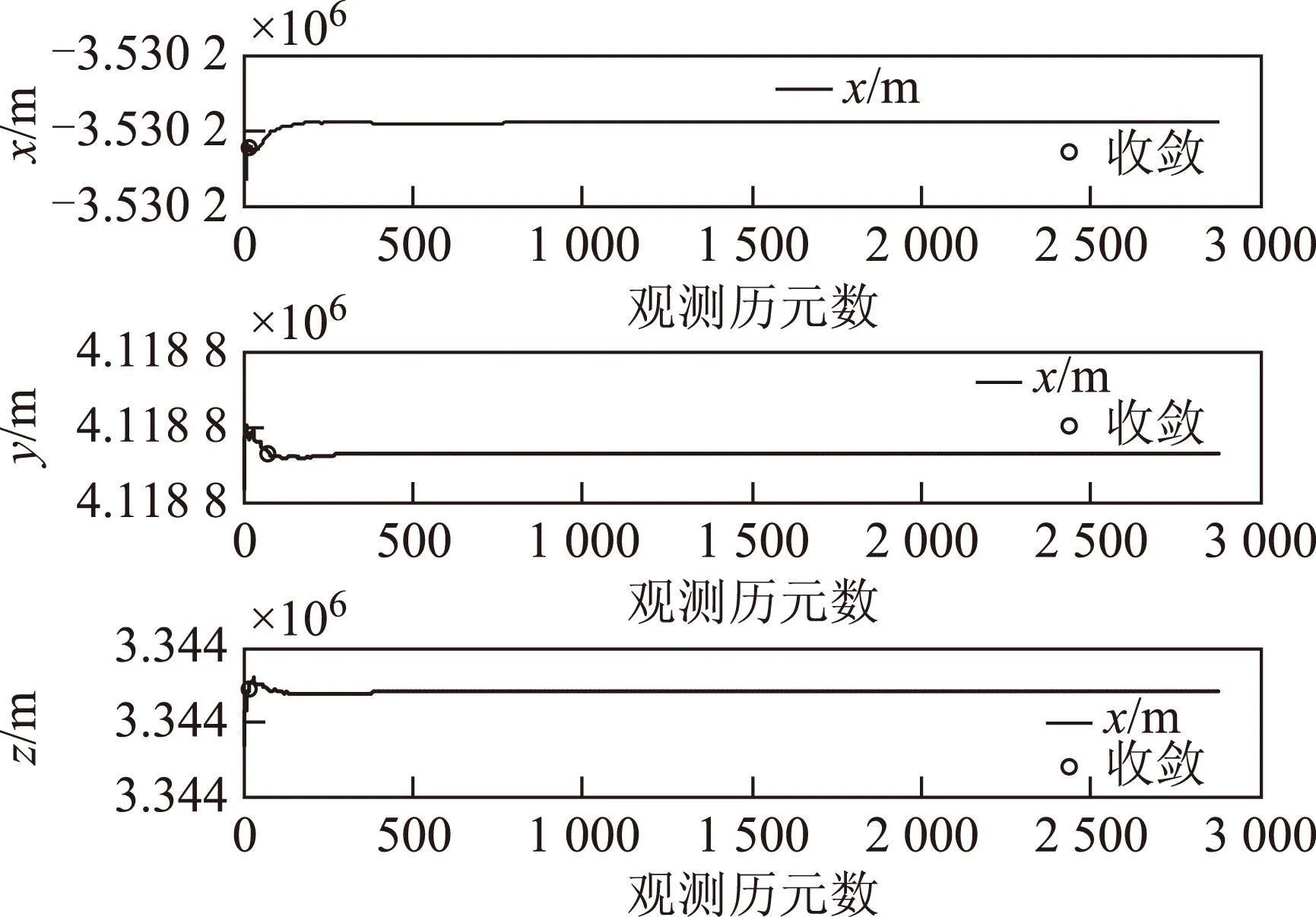
图2　收敛判断图(均值变化法)

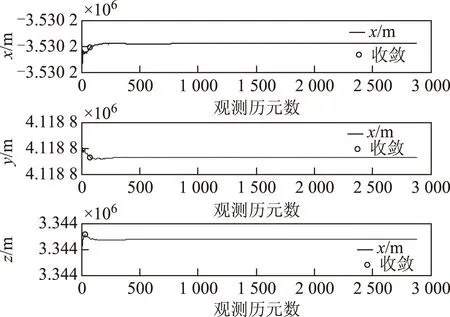
图3　收敛判断图(方差变化法)

在不同阈值d的情况下，两种方法的搜索窗口与收敛时间(收敛历元)的关系如图4、图5：

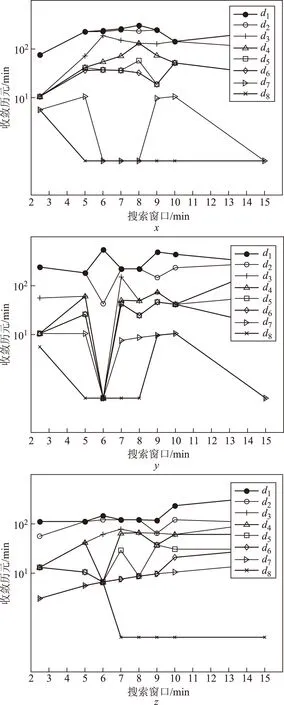
图4　不同阈值d下搜索窗口与收敛时间关系图(均值变化法)

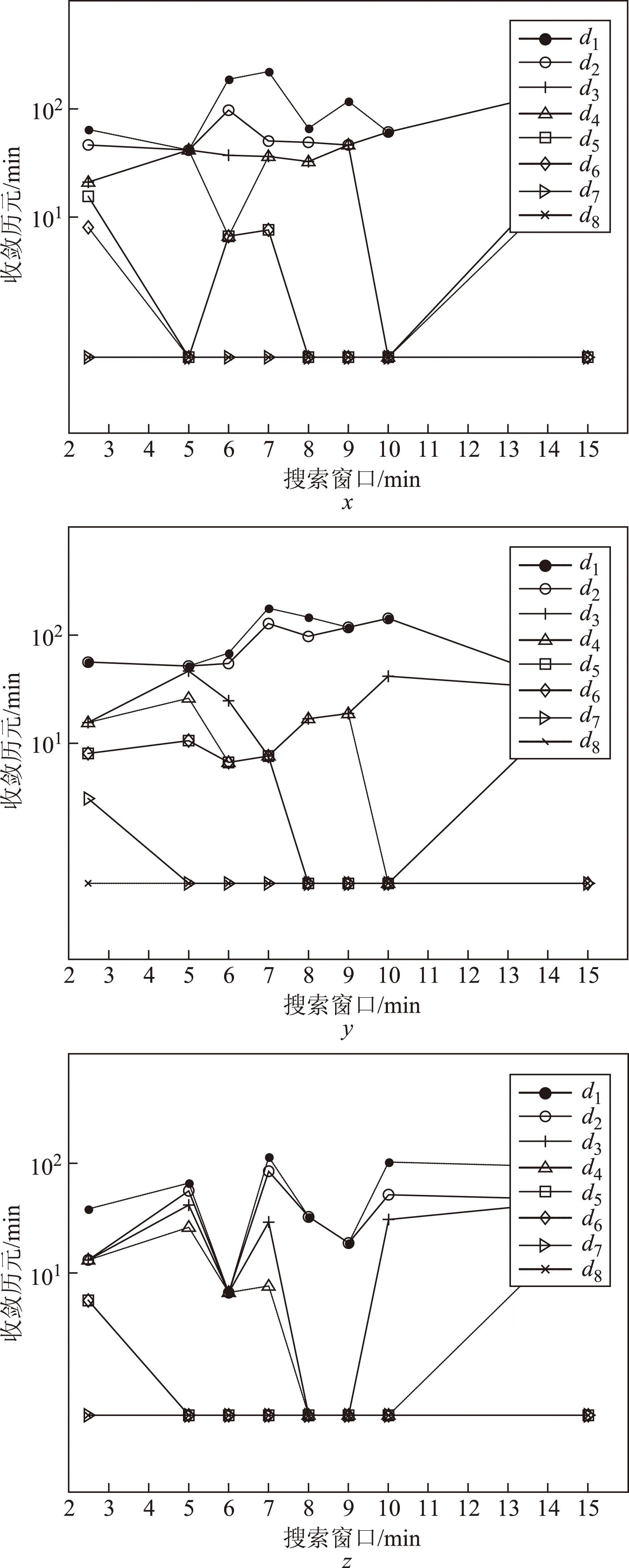
图5　不同阈值d下搜索窗口与收敛时间关系图(方差变化法)

根据图4及图5，得出结论：

1)收敛时间在数分钟到100 min范围内；

2)在相同的搜索窗口下，阈值d越小，收敛时间越长；

3)在相同的阈值d下，随着搜索窗口的增大，收敛时间变化规律不明显，但总体呈先增、再减、再增的趋势；

4)方差变化法的收敛时间对阈值的取值相对敏感，例如在阈值d8=4×10-2时，其收敛时间为3 min左右，且不随搜索窗口变化，这种情况下将导致无法有效确定收敛时间。

另外，坐标三方向的收敛历元与定位偏差存在一定关系，根据图6及图7，得出结论：

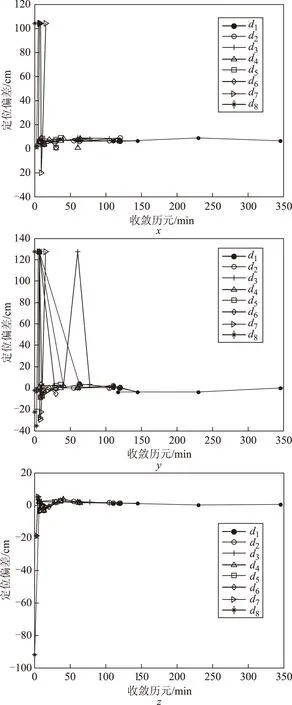
图6　不同阈值d下收敛历元与定位偏差关系图(均值变化法)

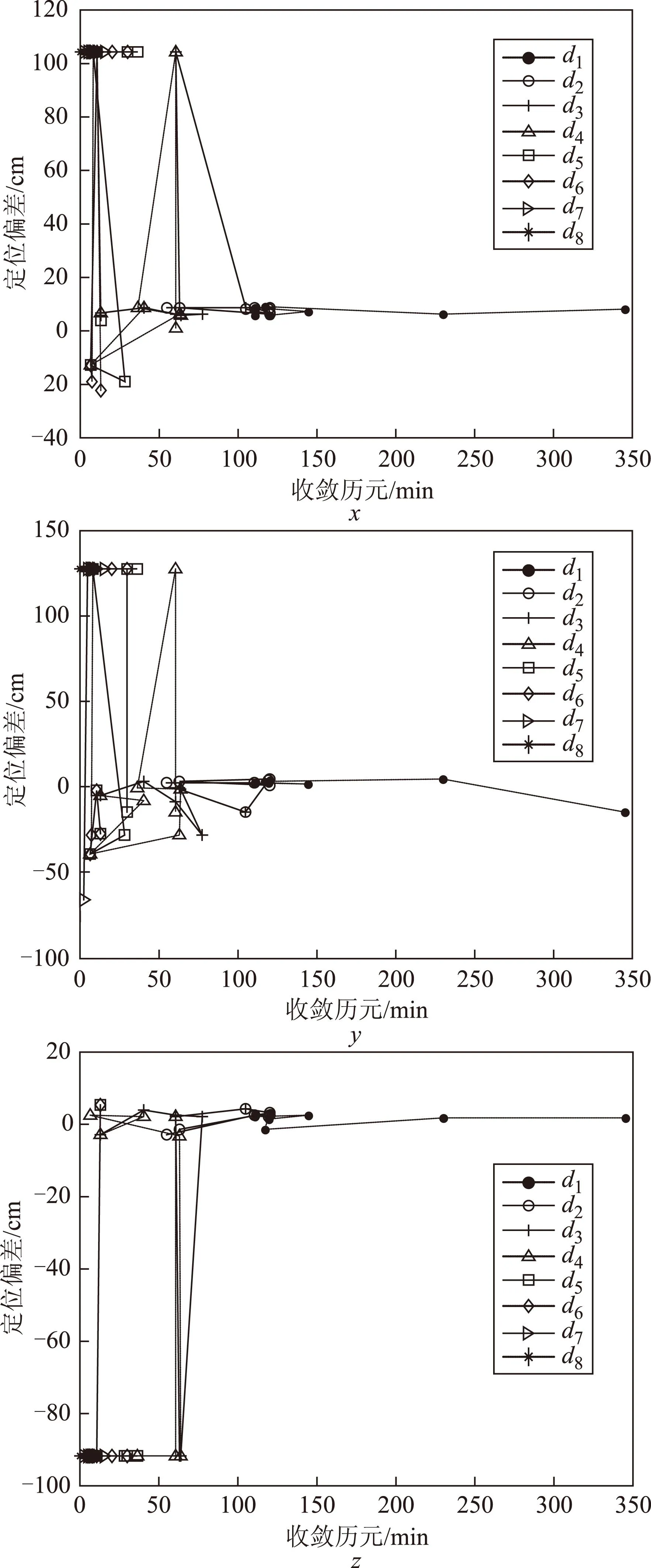
图7　不同阈值d下收敛历元与定位偏差关系图(方差变化法)

1)两种方法的定位偏差在能达到dm级甚至cm级；

2)阈值一定的情况下，收敛历元数越大，定位偏差越小；

3)在相同搜索窗口的情况下，方差变化法的定位偏差在不同阈值下差异较大，对阈值相对敏感。

3.2实验分析

为了比较两种方法的性能，需要获取跟踪站坐标三方向时间序列的实际收敛时间，将两种方法判断出来的收敛时间与对应的实际收敛时间进行对比，收敛时间更接近实际收敛时间的，其方法的性能更优。为了获取10个全球跟踪站各自的实际收敛时间，可根据2015-08-20所属的IGS周解文件中的坐标精确值，与10个跟踪站的定位结果时间序列作差，判断其在不同定位偏差下的实际收敛时间。本文以定位偏差为5 cm、1 dm时，用两种方法判断出来的收敛时间与实际收敛时间的接近程度为指标，比较两种方法的性能。对所有跟踪站，将两种方法下的所有阈值和搜索窗口组合确定出来的坐标三方向的收敛时间，与对应的实际收敛时间相比，当只有一方向的收敛时间等于实际值时，归为“一类”；两方向等于实际值时归为“二类”；三方向都等于实际值时归为“三类”，统计上述三类的数量(同时也考虑不同阈值和搜索窗口的组合可能会确定出相同的收敛时间)，统计结果如图8。由图8可明显看出，总体上，均值变化法确定出的收敛时间更接近于实际值。

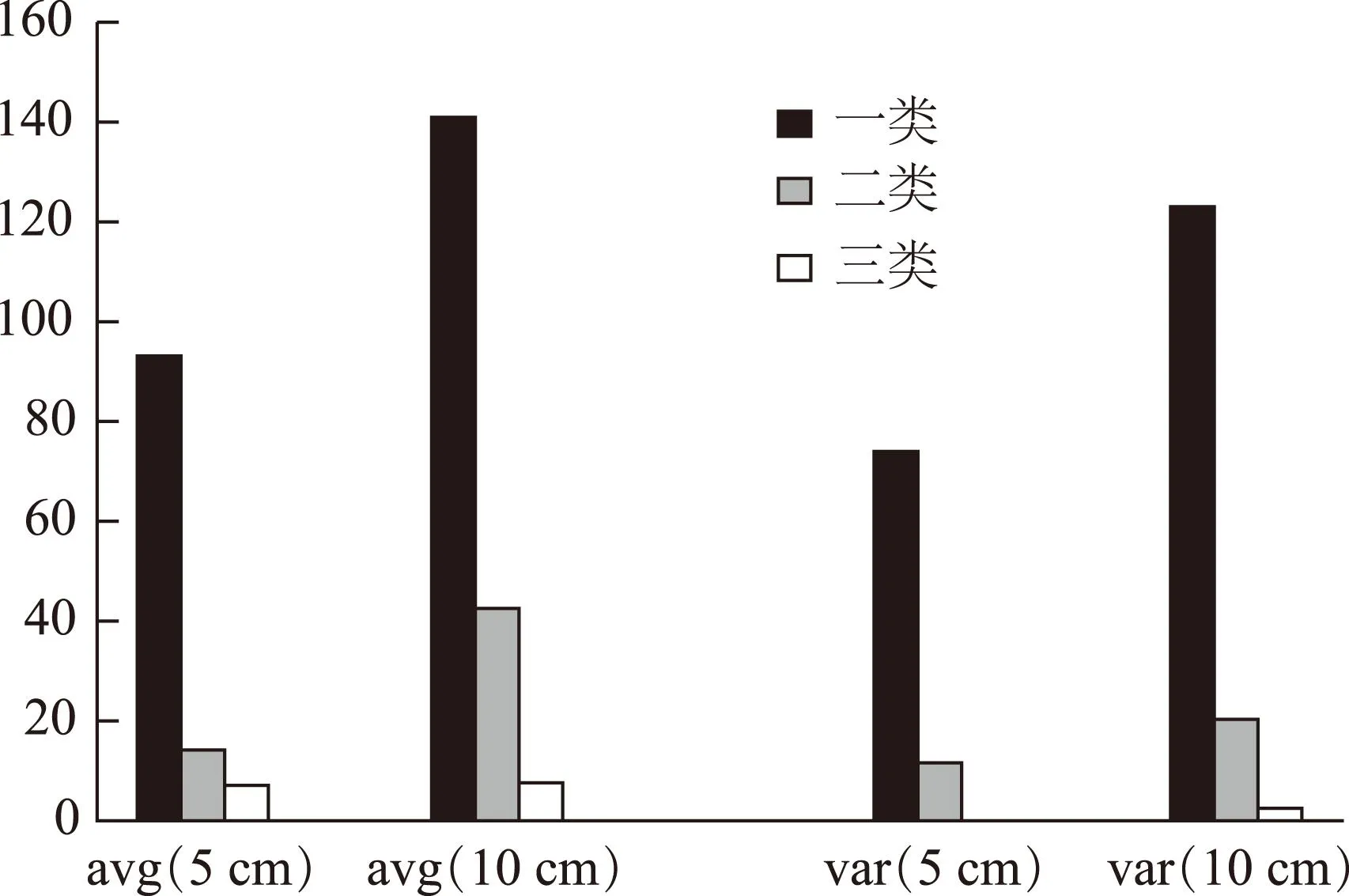
图8　收敛时间接近实际值的数量图

考虑到收敛的时效性，由图4至图7可得，阈值不是越小越好，搜索窗口不是越长越好，它们存在最优组合，在保证收敛的时效性前提下，使得定位偏差最小。为确定阈值与搜索窗口的最优组合，可将图8中“一类”、“二类”和“三类”类中的元素与其对应的d、k关联起来：显然“三类”类中的d、k组合应该最逼近最优组合，其次是“二类”类，最后是“一类”类。综合考虑，本文采取加权积分的方式，将10分按照比例1∶3∶6分配给“一类”、“二类”和“三类”类中的d、k组合，统计不同d、k组合的积分，最后再将各组合按照积分比例加权，计算得到最优组合。经计算，两种方法在定位偏差为5 cm和1 dm时，阈值、搜索窗口最优组合如表1。

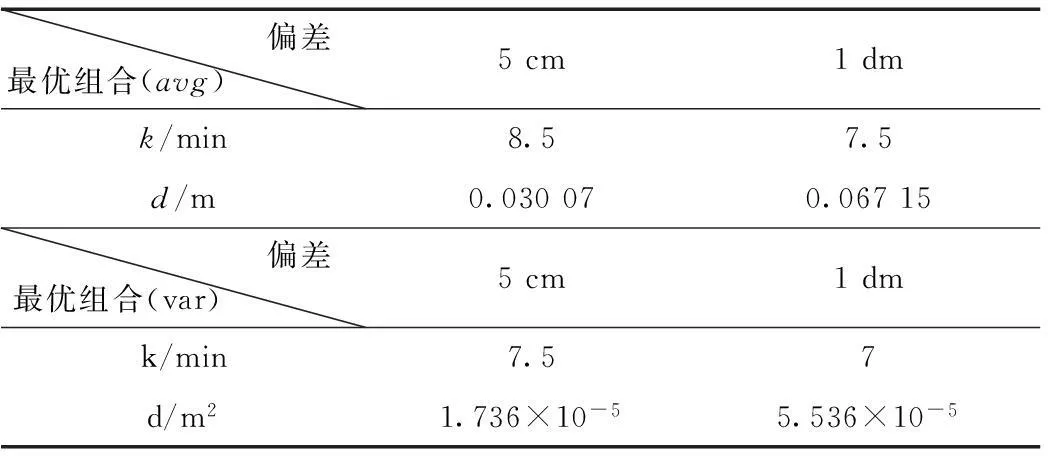
表1　最优组合

表1给出了两种方法的最优组合，为了保证最优组合的可靠性，采取实验验证的方法。验证数据为2014-01-02～2015-01-02 adis、aira、algo、bjco和bjfs五个跟踪站的全年数据，由于实验所用的精密星历和精密钟差是按日存储，故需对每个跟踪站进行366次实验。利用两种方法的最优组合，对验证数据定位解算、实时收敛判断，再确定定位偏差，其结果如表2至表5。

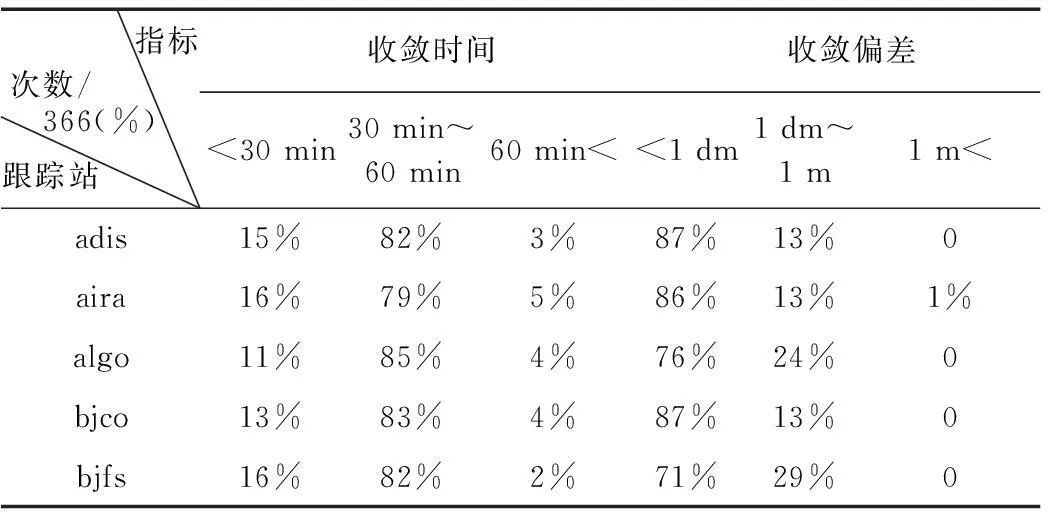
表2　均值变化法最优组合的验证(5 cm 偏差)

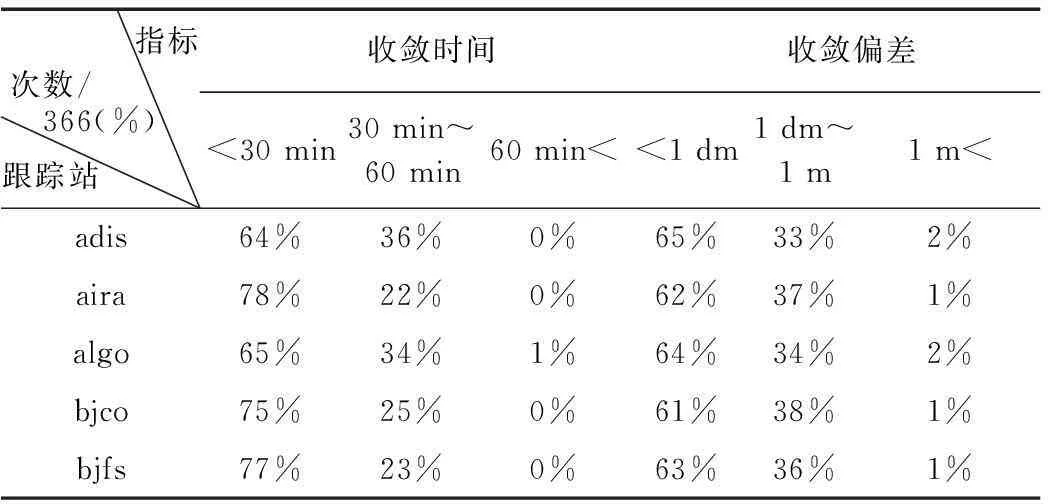
表3　均值变化法最优组合的验证(1 dm 偏差)

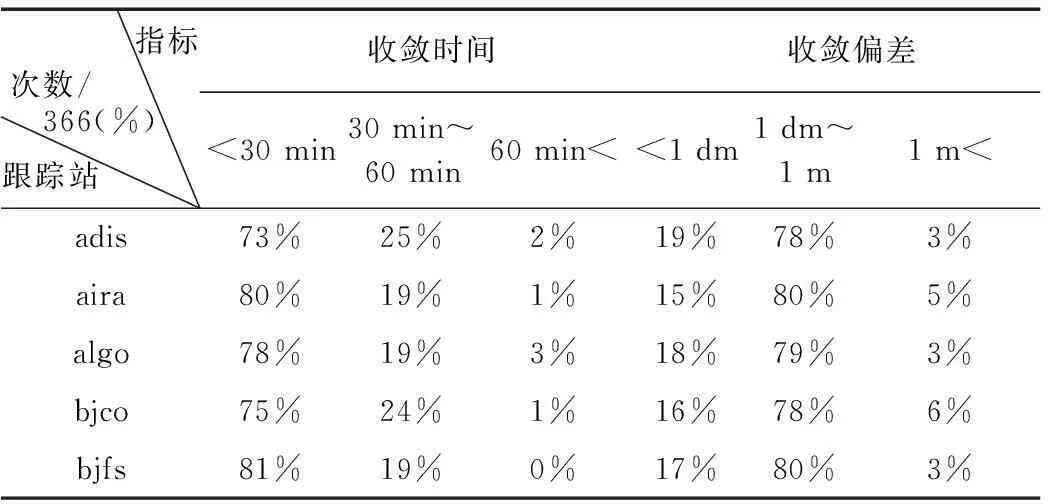
表4　方差变化法最优组合的验证(5 cm 偏差)

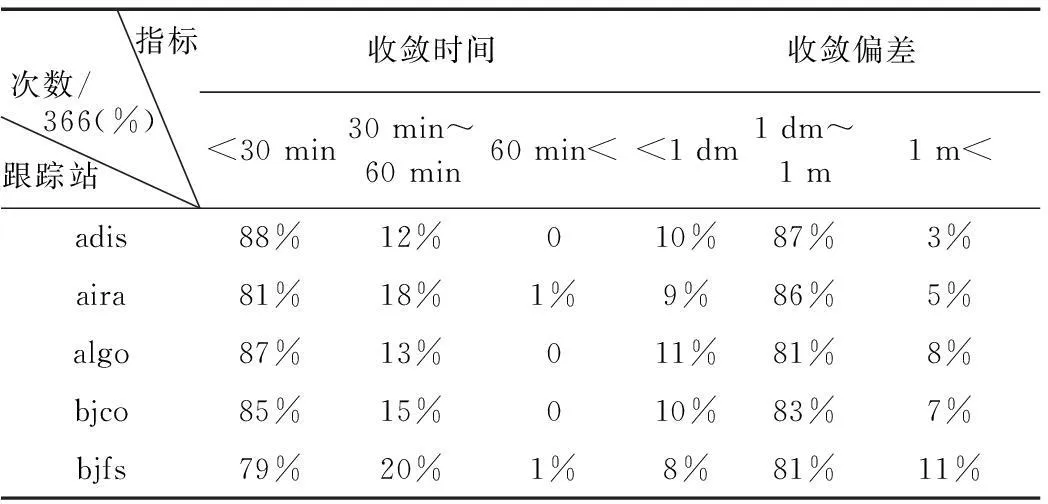
表5　方差变化法最优组合的验证(1dm 偏差)

从表2至表5中分析得：

1)利用一年的数据对5个跟踪站分别进行366次实验，共1 830次实验；

2)均值变化法中偏差5 cm对应的最优组合，在所有实验中有81.4%能收敛到cm级，且有82%的实验在30～60 min内收敛；偏差1 dm对应的最优组合，98.6%的实验能收敛到dm级至亚m级内(包括63%能收敛到cm级的实验)，且有72%的实验在30 min内收敛；

3)方差变化法中偏差5 cm对应的最优组合，在所有实验中只有17%能收敛到cm级，且有77.4%的实验在30 min内收敛；偏差1 dm对应的最优组合，93.2%的实验能收敛到dm级至亚m级内(包括9.6%能收敛到cm级的实验)，且有84%的实验在30 min内收敛；

4)方差变化法中出现m级误判偏差的概率明显高于均值变化法；

5)均值变化法确定出的收敛时间要稍长于方差变化法。

4结束语

本文利用15个IGS跟踪站的实验数据，分析验证了基于均值变化和方差变化的两种PPP收敛时间确定方法的可行性，同时也用大量数据证明了最优组合的可行性。但值得注意的是，实验中最优组合是基于事后精密星历产品定位的经验值，该经验值只适用于事后PPP，不具有通用性，但基于快速精密星历产品定位或预报精密星历产品的实时PPP的最优组合经验值同样可以通过本实验中的方法获取。

通过大量数据实验，证明均值变化法和方差变化法都具有确定收敛时间的能力，收敛时间大都在30 min级，不超过60 min，但均值变化法确定的收敛时间要稍长于方差变化法。另外，均值变化法能收敛到cm级至dm级，方差变化法能收敛到dm级，但会出现m级的误判偏差。分析实验结果可得，方差变化法中的阈值选取不当会使收敛精度相对较差，导致m级定位偏差，且该方法的阈值是均值变化法阈值的平方量级，跨度较大，易出现选取不当的情况，最终导致方差变化法性能不稳定。因此，根据PPP定位结果时间序列的特点，考虑误判概率，对比两种PPP收敛时间的确定方法，均值变化法要优于方差变化法。

参考文献

[1]刘经南，叶世榕.GPS非差相位精密单点定位技术探讨[J].武汉大学学报·信息科学版，2002，27(3)：234-235.

[2]ZUMBERGE J F，HEFLIN M B，JEFFERSON D C.Precise point positioning for the efficient and robust analysis of GPS data from large network[J].Journal of Geophysical Research：Solid Earth，1997，102(B3)：5005-5017.

[3]GAO Yang，SHEN Xiaobing.Improving ambiguity convergence in carrier phase-based precise point positioning[C]//The Institute of Navigation(ION).Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GPS 2001.Salt Lake City，UT：ION，2001：1532-1539.

[4]张小红，刘经南，FORSBERG R.基于精密单点定位技术的航空测量应用实践[J].武汉大学学报·信息科学版，2006，31(1)：19-22.

[5]郑艳丽.GPS非差精密单点定位模糊度固定理论与方法研究[D].武汉：武汉大学.2013：1-70.

[6]施闯，赵齐乐，楼益栋，等.卫星导航系统综合分析处理软件PANDA及研究进展[J].航天器工程，2009，18(4)：64-70.

[7]ZHANG Xiaohong，ZUO Xiang，LI Pan，et al.Convergence time and positioning accuracy comparision between BDS and GPS precise point positioning[J].Acta Geodaetica et Cartographica Sinica，2015，44(3)：250-256.

[8]梁寅，李星星，畅毅，等.静态精密单点定位的精度和收敛性分析[J].测绘工程，2010，19(2)：32-34.

[9]林晓静，张小红，郭斐，等.影响精密单点定位收敛速度的因素分析[J].测绘信息与工程，2010，35(3)：10-12.

[10]叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉：武汉大学，2002：6-10.

[11]肖辉.时间序列的相似性查询与异常检测[D].上海：复旦大学，2005：71-72.

[12]易重海.实时精密单点定位理论与应用研究[D].长沙：中南大学，2011：19-20.

[13]葛春蕾.时间序列的变点估计的相合性和收敛速度[D].合肥：合肥工业大学，2007：16-18.

A Study of Methods in Determining The Precise Point Positioning Convergence Time

ZHOUChengsong1，PENGYue2，3，ZHANGXiaohong2，LIUWenxiang1，WANGFeixue1

(1.School of Electronic Science and Engineering, National University of Defense Technology，Changsha 410073，China；2.School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China；3.Sichuan Bureau of Surveying Mapping and Geoinformation，Chengdu 610100，China)

Abstract：According to the efficiency problem of precise point positioning(PPP)，this article proposes two methods to determine the PPP convergence times based on the mean and variance changes，and expounds the principle of these methods respectively.PPP is a calculation of position with observation data and the relevant satellite orbit and satellite clock error，finally gets the PPP time series of positioning results.This time series has the characteristic that from non-stationary to smooth and steady.In engineering applications，due to the lack of a method in determining the PPP convergence time，so the PPP observation time which often reaches several hours or even more is usually longer than the convergence time，thus the redundant observations make the work inefficient.This article analyzes if the performance of the two methods in determining the convergence time timely or accurately based on large volumes of measured data，the results show that both the two methods can decide the convergence time，the convergence time decided by the mean-change method is slightly longer than the convergence time decided by the variance-change method，but the convergence time decided by the two methods is mainly in 30min，not longer than 60min.The mean-change method can converge from decimeters to centimeters.The variance-change method can converge to decimeters，but there is meters-miscalculation deviation.

Key words：precise point positioning( PPP)；the time series；convergence time；performance analysis

中图分类号：P228

文献标识码：A

文章编号：2095-4999(2016)-01-0080-08

作者简介：第一周承松(1991—)，男，江西省吉安市人，硕士生，现从事卫星导航定位技术方面研究。

收稿日期：2015-10-21

引文格式：周承松，彭月，张小红，等.精密单点定位收敛时间的确定方法研究[J].导航定位学报，2016，4(1)：80-87.(ZHOU Chengsong，PENG Yue，ZHANG Xiaohong，et al.A Study of Methods in Determining The Precise Point Positioning Convergence Time[J].Journal of Navigation and Positioning，2016，4(1)：80-87.)DOI：10.16547/j.cnki.10-1096.20160116.