卫星导航RAIM多星故障检测与识别方法研究

邓志鑫，李　隽，刘孟江

(1.中国电子科技集团公司 第五十四研究所，石家庄　050081；2.卫星导航系统与装备技术国家重点实验室，石家庄　050081)



卫星导航RAIM多星故障检测与识别方法研究

邓志鑫1，2，李隽1，2，刘孟江1，2

(1.中国电子科技集团公司 第五十四研究所，石家庄050081；2.卫星导航系统与装备技术国家重点实验室，石家庄050081)

摘要：针对传统卫星导航接收机自主完好性监测RAIM方法在多颗故障卫星情况下故障识别的检测概率低、虚警概率高的问题，提出一种检测概率较高、虚警概率低、同时具有低运算量、可工程化实施的RAIM多星故障检测与识别方法，文中分别阐述方法的原理及及其仿真分析，结果表明本方法在无虚警情况下获得了较高的检测概率。本方法具有非常低的运算量，在具有m(m>0)颗故障卫星的情况下，通常仅需要2 m次最小二乘残差故障检验和m次故障识别，具有较高的应用价值。

关键词：RAIM；多星故障检测；多星故障识别；多历元平滑

0引言

卫星导航完好性是卫星导航系统的重要服务性能之一，用户需要在导航卫星发生故障时及时感知并排除故障卫星，从而获得连续而正确的定位结果。接收机自主完好性监测(receiver autonomous integrity monitoring，RAIM)相对于卫星导航系统而言能够实现卫星故障的快速监测。RAIM需要解决两个问题：卫星是否存在故障和故障存在于哪颗卫星。

较早出现的RAIM算法有卡尔曼滤波方法和定位解最大间隔法。卡尔曼滤波方法可以利用过去观测量提高效果，但必须给出先验误差特性，而实际误差特性很难准确预测，如果预测不准，反而会降低效果。定位解最大间隔法的数学分析过程较复杂，故障检测的判决门限不易确定。较好的RAIM算法是仅利用当前历元伪距观测量的“快照”方法，包括伪距比较法、最小二乘残差法和奇偶矢量法。这三种方法对于存在一个故障偏差情况都有较好效果，并且是等效的。但是这三种方法在存在多个故障偏差时故障识别的效果很差，识别率仅有40%至60%，这是因为这些方法均采用检测统计量与固定门限相比较的方式来进行故障识别，当出现多个故障偏差时，由于故障偏差在检测统计向量中发散，导致难以正确识别。

综上所述，采用传统方法进行多星RAIM故障检测和识别时，检测概率过低，虚警概率较高，近期提出的新方法计算量过大，不适合广泛应用，尤其是数据更新率较高的接收设备难以应用。

1最小二乘残差法RAIM故障检测与识别

1.1最小二乘残差模型

具有n颗可观测卫星的全球导航卫星系统(global navigation satellite system，GNSS)伪距观测模型为

Y=G·X+ε

(1)

式(1)中，Y是观测伪距与计算得到的伪距的差值的n维矢量；X是四维未知矢量，含三个位置改正数和一个接收机钟差改正数；ε为n维伪距观测噪声矢量；G是n×4维的系数矩阵，有

(2)

式(2)中，[x(i),y(i),z(i)]T为卫星i的位置坐标向量，[x,y,z]T为解算出来的用户位置坐标向量，r(i)为用户与卫星的观测距离。

最小二乘残差RAIM法是基于残差平方和的χ2检验进行卫星整体故障检测，并利用残差元素的高斯检验进行卫星故障识别，从而实现完好性监测。

(3)

令伪距残差向量的协因数阵为：Qv=I-G(GTG)-1GT， 则v=QvY。 向量v中包含了卫星测距的误差信息，可以用于判断卫星是否存在故障的依据。故障检测的统计检验量为

(4)

式(4)中，SSE(sum of the squares of range residual errors)作为伪距残差向量中各个元素的平方和，是一个自由度与观测到的导航系统数目有关的χ2分布。

1.2故障检测与识别

为了判定是否具有故障，可作二元假设，即

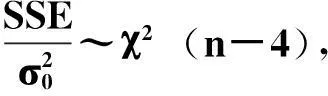
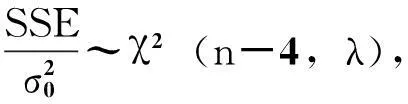
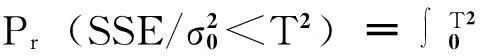
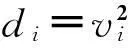
2新型RAIM多星故障检测与识别方法

上述最小二乘残差RAIM故障检测与识别方法主要存在如下问题：

(1)当存在多颗故障卫星时，非常容易导致粗差在故障识别的检测统计量中发散，从而发生漏检和虚警，即使单颗卫星故障时采用极大似然的估计方法也会降低检测概率和提升虚警概率；

(2)由于卫星是否有故障在一段时间内并不会发生剧烈变化，因此单历元的检测结果并不可信，如果发生漏检或虚警的情况，都会或大或小地损失用户的服务性能。

针对传统最小二乘残差RAIM故障检测与识别方法的上述问题，以该方法作为基础，提出了一种低运算量的新型RAIM多星故障检测与识别方法，其工作流程为：

(3)在每一历元采用最小二乘残差法与极大似然法单步逐级检测故障并估计故障卫星，直到获得无故障星座为止，得到初始故障检验结果(含是否存在故障和故障卫星号)；

(4)以初始无故障星座为基础对检测出的故障卫星进行逐一验证，确认其是否具有故障，并得到本历元验证后的故障检验结果；

(5)对当前历元故障检验结果与当前历元之前最近两个历元的故障检验结果进行平滑后得到当前历元的最终故障检验结果。

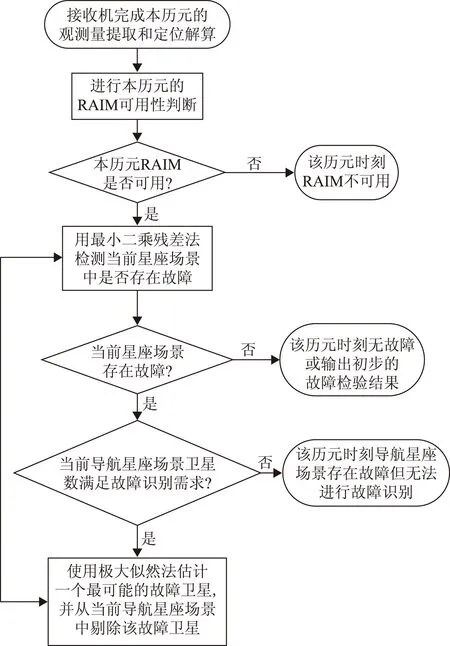
图1　单历元初始故障检验工作流程

步骤(1)中单历元初始故障检验的工作流程如图1所示，其具体工作步骤为：

1)接收机进行RAIM可用性判断，如果RAIM可用，则转入步骤2)，否则输出该历元时刻RAIM不可用的初步故障检验结果；

2)接收机通过最小二乘残差法检测当前导航星座场景中是否存在故障；如果存在故障，则转入步骤3)，否则转入步骤4)；

3)如果该历元当前导航星座场景中的卫星数满足故障识别需求，则利用极大似然法估计一个最可能的故障卫星，并从当前导航星座场景中剔除该故障卫星，之后转入步骤2)；如果不满足故障识别需求，则转入步骤4)；

4)如果当前导航星座场景存在故障并且导航星座场景中的卫星数满足故障识别需求，则输出该历元时刻的初步故障检验结果；如果当前导航星座场景存在故障但导航星座场景卫星数不满足故障识别需求，则输出该历元导航星座场景存在故障但无法进行故障识别的初步故障检验结果；如果当前导航星座场景不存在故障，则输出该历元无故障的初步故障检验结果。

步骤(2)中对故障卫星进行逐一验证的工作流程如图2所示，其具体工作步骤为：

1)判断是否存在待验证的故障卫星，如果存在则选取一颗待验证故障卫星，将该故障卫星的原始观测信息加入到当前的无故障星座场景中，并转至步骤2)，如果不存在待验证的故障卫星则转至步骤3)；

2)利用新构建的星座重新进行最小二乘残差法故障检测，如果未检测到故障，则将该卫星标志为无故障卫星，如果检测到故障，则将该卫星标志为有故障卫星，同时将该卫星观测信息从当前星座场景中剔除，然后转至步骤1)；

3)输出该历元时刻经验证后的故障检验结果，包括当前场景中是否存在故障以及所有故障卫星号。

图2　对故障卫星进行逐一验证的工作流程

步骤(3)中对多历元故障检验结果进行平滑的工作流程如图3所示，多历元故障检验平滑的具体方法为：判断最近三个历元的故障检验结果中是否包含两个或两个以上的该历元RAIM不可用的故障检验结果，如果包含，则将该结果作为当前历元最终故障检验结果；如果不包含，则判断最近三个历元的故障检验结果中是否包含两个或两个以上的该历元时刻导航星座场景存在故障但无法进行故障识别的故障检验结果，如果包含，则将该结果作为当前历元最终故障检验结果；如果不包含，则判断最近三个历元的故障检验结果中是否存在两个或两个以上完全相同，如果存在，则将这一相同的故障检验结果作为当前历元最终故障检验结果；如果不存在，则将该历元时刻导航星座场景存在故障但无法进行故障识别作为当前历元最终故障检验结果。

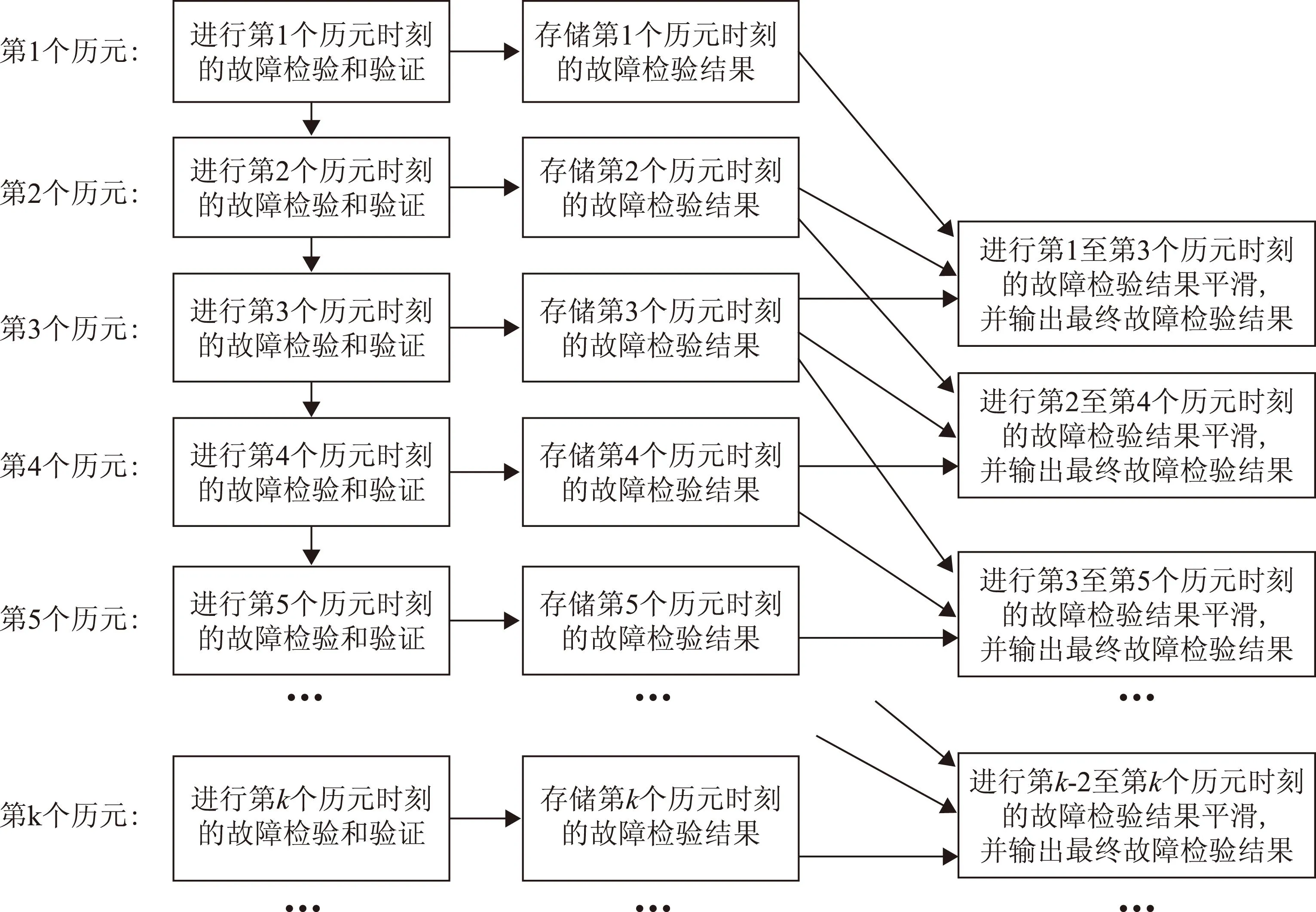
图3　多历元故障检验结果平滑工作流程

3算法性能仿真验证

下面对新型RAIM多星故障检测与识别方法进行性能仿真验证，仿真条件为：场景卫星数量12颗，场景GDOP值为1.605 5，RAIM检测的虚警概率为0.001，定位解算预设精度为0.001 m，概率统计时每次仿真验证次数为1 000，每次采样依据设定的卫星数量随机选择故障卫星。若未特殊指定，则接收机伪距噪声0.25 m，故障卫星的伪距误差为±10 m左右的随机值。每颗星的故障检验结果(有故障或无故障)与预设结果均完全符合，则认为该组检验结果正确，否则不正确。这种判断机制既关心有故障时未检测，也关心误警。

图4为不同RAIM故障检测与识别算法情况下故障卫星数量与无虚警正确检验概率之间的关系，其中仿真了三种情况，分别是单历元初始故障检验(仅含步骤(1))、单历元故障检验(含验证，包括步骤(1)和(2))、三历元故障检验结果平滑(包括步骤(1)、(2)和(3))的故障检测与识别性能。由图可知，单历元初始故障检验已经比传统最小二乘残差法多星故障识别概率大幅提高，经过步骤(2)的故障卫星验证和步骤(3)的多历元检验结果平滑，每一步都使得多星故障识别概率得到有效提升，尤其是在场景中存在3颗、4颗、5颗故障卫星时，改进方法的提升效果较为明显。

图4　不同RAIM算法的故障检验性能

根据仿真程序输出的具体检测概率值，完成RAIM故障检测与识别步骤(1)、(2)和(3)后，无故障卫星和具有1颗故障卫星情况下，故障检测与识别的正确检验概率均为100%，当存在2颗故障卫星时，故障识别的正确检验概率大于98%，当存在3颗故障卫星时，故障识别的正确检验概率为90%左右，当存在4颗故障卫星时，故障识别的检验概率为65%至70%左右。

图5为不同故障卫星数量情况下，故障伪距值相对于伪距噪声标准偏差的倍数与无虚警正确检验概率之间的关系。由图可知，当故障伪距值为伪距噪声的8～9倍及以上时，正确检验概率达到最大，算法性能达到最大程度发挥。

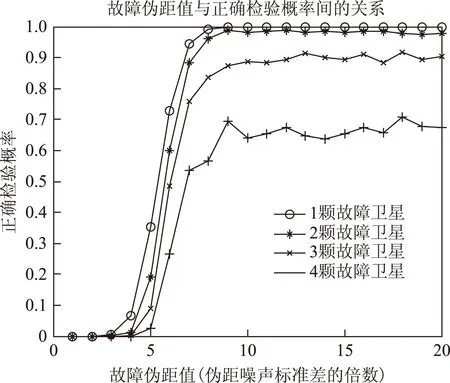
图5　故障伪距值与无虚警正确检验概率之间的关系

图6为不同故障卫星数量情况下，当故障伪距值为10 m左右时，伪距噪声与无虚警正确检验概率之间的关系。由图可知，当伪距噪声大于1.2 m(10 m的1/8.3)时，故障检验性能开始下降，这与图6所得出的结论是一致的。

4结束语

综上所述，可以总结出本文所提出的卫星导航RAIM多星故障检测与识别方法具备如下优势：通过最小二乘残差法和极大似然法单步逐级检测与识别多颗故障卫星，在不明显增加运算量的条件下有效提升了传统故障识别方法的检测概率；通过对初步筛选的故障卫星进行逐一验证的方式有效降低了RAIM算法的虚警概率，从而增加了无故障星座的卫星数目；采用多历元故障检验结果平滑方法进一步提高了故障检测概率，降低了虚警概率。

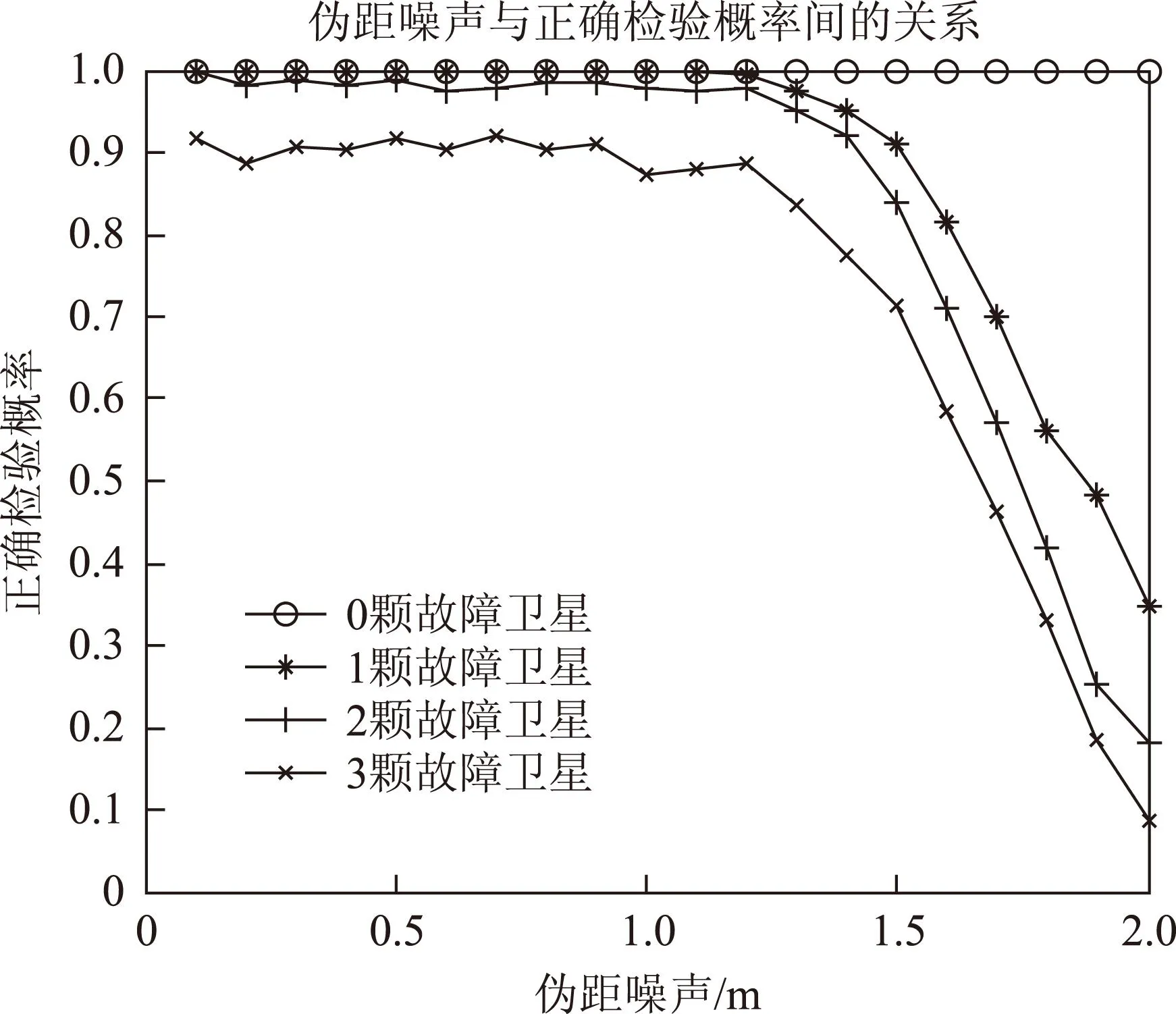
图6　伪距噪声与无虚警正确检验概率之间的关系

本文所提供的RAIM多星故障检测与识别方法相对于背景技术中阐述的各种新方法而言，具有非常低的运算量，在具有m(m>0)颗故障卫星的情况下，通常仅需要2 m次最小二乘残差故障检验和m次故障识别，具有较高的应用价值。

参考文献

[1]孙淑光.基于极大似然比的多故障卫星完好性检测[J].中国惯性技术学报，2011，19(3)：312-315.

[2]陈灿辉，张晓林.全球导航卫星系统多星故障排除新方法[J].北京航空航天大学学报，2011，37(12)：1479-1483.

[3]张强，张晓林，常啸鸣.用于卫星导航多星故障识别的新方法[J].航空学报，2008，29(5)：1239-1244.

[4]陈小平，滕云龙.接收机自主完好性监测算法研究[J].电子科技大学学报，2008，37(2)：218-220.

[5]HWANG P Y，BROWN R G.RAIM FDE revisited：A new breakthrough in availability performance with NIORAIM(Novel integrity-optimized RAIM)[C]//The Institute of Navigation.Proceedings of the ION NTM.San Diego，CA：The Institute of Navigation，Inc.，2005：654-665.

[6]MACABIAU C，GERFAULT B，NIKIFOROV I，et al.RAIM performance in presence of multiple range failures[C]//The Institute of Navigation.Proceedings of the ION NTM.San Diego，CA：The Institute of Navigation，Inc.，2005：779-791.

[7]BLANCH J，ENE A，WALTER T，et al.An optimized multiple hypothesis RAIM algorithm for vertical guidance[C]//The Institute of Navigation.Proceedings of ION GNSS.Fort Worth，TX：The Institute of Navigation，Inc.，2007：2924-2933.

[8]ENE A.Further development of Galileo-GPS RAIM for vertical guidance[C]//The Institute of Navigation.Proceedings of ION GNSS.Fort Worth，TX：The Institute of Navigation，Inc.，2006：2597-2607.

[9]LEE Y C.Performance of receiver autonomous integrity monitoring (RAIM) in the presence of simultaneous multiple satellite faults[C]//The Institute of Navigation.The 60th Annual Meeting of the Institute of Navigation.Dayton，OH：The Institute of Navigation，2004：687-697.

[10]HEWITSON S，WANG Jinling.GNSS receiver autonomous integrity monitoring (RAIM) performance analysis[J].GPS Solutions，2006，10(3)：155-170.

Research on Multi Satellite Failure Detection and Recognition Method of Satellite Navigation RAIM

DENGZhixin1，2，LIJun1，2，LIUMengjiang1，2

(1.The 54thResearch Institute of CETC，Shijiazhuang 050081，China；2.State Key Laboratory of Satellite Navigation System and Equipment Technology，Shijiazhuang 050081，China)

Abstract：In order to solve traditional satellite navigation receiver autonomous integrity monitoring (RAIM) problems，just like the low fault detection probability and the high false alarm probability，the RAIM satellite fault detection and recognition method is proposed in this paper，which has a high detection probability，a low false alarm probability，low computation cost，and is suitable for project implementation.This method has carried on the simulation analysis，the results show that this method has obtained higher detection probability in the case without false alarm.The computation of this method is very low，with m(m>0) faulty satellites situation，usually only need 2 m times least squares residuals fault detection and m times fault identification，so it has high application value.

Key words：RAIM；multi satellite failure detection；multi satellite failure recognition；multi epoch smoothness

中图分类号：P228

文献标识码：A

文章编号：2095-4999(2016)-01-0075-05

作者简介：第一邓志鑫(1982—)，黑龙江哈尔滨人，博士，高级工程师，主要研究方向为卫星导航。

基金项目：国家863计划(2012AA121801)。

收稿日期：2015-05-20

引文格式：邓志鑫，李隽，刘孟江.卫星导航RAIM多星故障检测与识别方法研究[J].导航定位学报，2016，4(1)：75-79.(DENG Zhixin，LI Jun，LIU Mengjiang.Research on Multi Satellite Failure Detection and Recognition Method of Satellite Navigation RAIM[J].Journal of Navigation and Positioning，2016，4(1)：75-79.)DOI：10.16547/j.cnki.10-1096.20160115.