一类特殊数列求和问题的处理策略
2016-04-06朱玲,吴智
一类特殊数列求和问题的处理策略
湖北省武汉经济技术开发区第一中学(430056)朱玲吴智
数列问题一直是高考的高频考点,也是高三复习备考的主干知识.近几年在全国及各省市的高考卷中陆续出现了一些递推式中含(-1)n的数列求和问题,这些问题处理方法大同小异,只要掌握基本方法和原理,完全可以做到逢题必会,逢考必胜.下面,笔者给出这类问题的几种处理策略,以飨读者.
策略一:形如an=(-1)n·f(n),用并项求和法处理
所谓并项求和法,就是将待求数列的前n项和“化整为零”,把位置相邻的两项结合在一起,研究它们的内在规律,找出an+an+1的定值关系或表达式,从而实现问题的解决.



例2数列{an}的通项公式为an=(-1)n-1·(4n-3),则它的前100项之和S100=.
解析:S100=(a1+a2)+(a3+a4)+…+(a99+a100),又an+an+1=(-1)n-1·[(4n-3)-(4n+1)]=(-1)n·4,当n为奇数时,an+an+1=-4,故S100=50×(-4)=-200.
策略二:形如φ(an+m,(-1)nan)=f(n),用奇偶讨论和分组求和法处理
已经关停的油井,是否还有必要恢复?读罢贵刊2018年第19期刊登的报道《“唤醒”关停井》一文,得出的答案不仅是“有必要”,而且是“油田企业扭亏脱困的重要手段”。
这类问题的处理相对比较复杂,但仍有章可循,有“法”可依.往往需要对n分奇偶讨论,找到相邻两个奇(偶)数项之间的变化规律,然后利用分组求和法处理.
例3(2012年新课标全国卷第16题)数列{an}中,an+1+(-1)nan=2n-1,则数列{an}的前60项和为.
解析:用2n、2n+1、2n-1分别替换an+1+
(-1)nan=2n-1中的n,得

例4在数列{an}中,a1=1,an+2+(-1)nan=1.记Sn是数列{an}的前n项和,则S100=.

策略三:形如φ(Sn,(-1)nan)=f(n),用奇偶讨论和阶差法处理
这类问题以能力立意,多设置在选填题的压轴或次压轴的位置.考查学生的逻辑推理和运算求解能力,对学生的综合能力要求较高.同策略二,可对n分奇偶讨论,同时施以阶差法的运用,问题得到巧妙解决.

解析:用2n、2n+1、2n-1分别替换Sn=



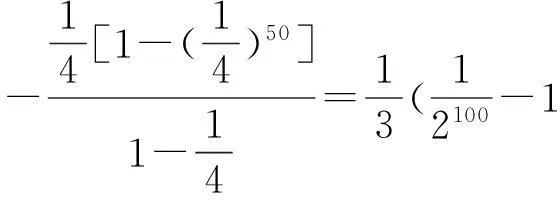
策略四:形如φ(an,(-1)nf(n))=k(f(n)中含有三角函数式,k为常数), 用归纳推理或奇偶讨论法处理.
这类问题比较简便的解法是利用归纳推理,结合三角函数的周期T,研究连续T项和的变化特征,从而归纳得到要求的结果.另外,也可以利用奇偶讨论法处理.

解法一:(归纳推理)由an=(-1)n(2n-1)·
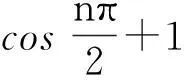


事实上,作为一道填空题,猜想的证明过程完全可以忽略不考虑.只要观察、发现连续四项和为定值这一隐含结论,问题便可迎刃而解.但作为归纳推理的应用,严谨的分析和推理还是很有必要的.


(-1)+(4n+3)·1+2=6.故S120=(a1+a3+…+a119)+[(a2+a4)+(a6+a8)+…+(a118+a120)]=60×1+6×30=240.
