试探以圆锥曲线的垂直弦为直径的圆



试探以圆锥曲线的垂直弦为直径的圆

湖北省武汉市第十四中学(430061)尹惠民

在研究与圆锥曲线有关的轨迹问题时，笔者对以圆锥曲线的两条垂直弦为直径的圆作了一番探索和演算，发现了下面的漂亮性质，希望与读者共享．

首先介绍将圆、椭圆、双曲线合三为一后得到的具有和谐、统一、对称美的一个性质．

定理1已知有心圆锥曲线E：mx2+ny2=1(当m、n都为正时是圆或椭圆，当m、n异号时是双曲线)，AB、CD是过曲线Γ内定点P(x0,y0)的两条互相垂直的弦,若以弦AB、CD为直径的两圆相交，则两圆公共弦恒过定点

图1

证明:(如图1)当直线AB、CD的斜率均存在且不为零时，设直线AB的方程为y=k(x-x0)+y0，代入mx2+ny2=1，并整理得

(m+nk2)x2+2kn(y0-kx0)x+n(y0-kx0)2-1=0，

=-n[mx0(1-k2)+(m+n)ky0]·(x-

所以两圆公共弦恒过定点

当直线AB、CD中有一条斜率不存在或为零时，可以验证两圆公共弦也过定点T．

另一方面，设以弦AB、CD为直径的两圆圆心分别为M、N，由圆方程③④易得

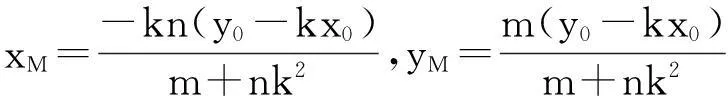
yN-yM=

由两点式得直线MN的方程为

(y-yM)(xN-xM)=(x-xM)(yN-yM)，即

(xN-xM)y=(yN-yM)x+yMxN-xMyN．

当直线AB、CD中有一条斜率不存在或为零时，可以验证两圆公共弦中点坐标满足轨迹方程．

经过研究发现在抛物线中也有类似的性质，证明略．