整体式连续斜板桥的实用计算方法
2016-04-06杨立坡
杨立坡
(天津市市政工程设计研究院,天津300051)
整体式连续斜板桥的实用计算方法
杨立坡
(天津市市政工程设计研究院,天津300051)
以不同斜交角度下整体式连续斜板桥为研究对象,提出了合理的钢筋配置方式.基于三弯矩方法,通过理论计算及有限元分析,总结了整体式连续斜板桥的实用计算方法,给出了实用计算图表.通过平面杆系的计算结果,查找相关系数即可以得到相应的配筋弯矩,简化了计算工作.
整体式连续斜板桥;实用计算方法;有限元
随着越来越多的整体式连续斜板桥应用在工程实际中,许多学者对其计算理论进行了广泛研究[1-3].斜交板桥与正交板桥的受力特性有很大差别[4],同时在实际工程设计中,由于各种因素,采用各种计算理论进行分析是不现实也是没有必要的,因此有必要基于整体式连续斜板桥的受力特性提出简化的计算方法,以指导实际工程设计.
1 整体式连续斜板桥的钢筋配置方式
对于整体式简支斜板桥,根据斜交角和宽跨比的不同,钢筋的配置方式是不同的.斜交角Φ>30°以及宽跨比b/L≥1∶3时,纵向及横向钢筋均平行于自由边;斜交角Φ>30°时,板内设置和支承边垂直的纵向钢筋,而横向钢筋则平行于支承边设置;斜交角Φ>20°以及宽跨比b/L<1∶2时,则设置和支承边平行及逐渐变至和自由边垂直的钢筋,在支座范围内钢筋成扇形布置.以上各种情况,均需在钝角区域设置局部受力钢筋.
整体式连续斜板桥若采用与简支斜板桥同样的配筋方式,必然导致设计和施工均很复杂,这显然违背了整体式连续斜板桥外形简单,设计施工均很方便的初衷.因此整体式连续斜板桥适宜的主筋配置方式为:纵向主筋平行于自由边,横向钢筋平行于支承边,纵向主筋与横向主筋的夹角即为板的斜交角.在钝角区域配置局部受力钢筋.主筋的配置如图1所示.

图1 整体式连续斜板桥的钢筋配置方式Fig.1 Reinforcement method of integral continuous skew girder bridge
2 整体式连续斜板桥的配筋弯矩
整体式连续斜板桥采用上述钢筋配置方式使得设计和施工都更加方便,但导致主筋方向与板的主弯矩方向不一致,两者存在夹角,因此应根据钢筋方向的弯矩配置主钢筋.本文求解钢筋方向主弯矩采用三弯矩方法,三弯矩即单元弯矩、主弯矩、配筋弯矩.
首先采用有限单元法计算单元中心的内力Mx,My,Mxy;
再根据求得的单元内力计算主弯矩和主弯矩方向M1,M2,α;
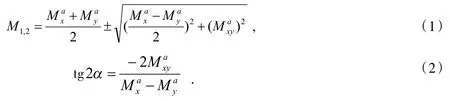
根据主弯矩及其方向,计算配筋方向的配筋弯矩.
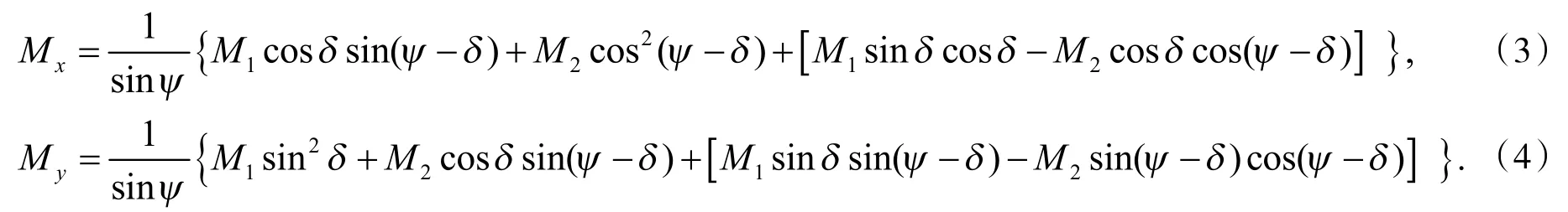
本文中采用的有限元软件Midas可直接得到各关键截面的主弯矩,因此仅需根据式(3)、式(4)求得配筋方向的配筋弯矩,即可根据求得的配筋弯矩配置纵横向主钢筋.式中各符号含义参见图2.

图2 斜板的主弯矩和配筋弯矩方向Fig.2 Directions of primary moment and reinforcement moment of skew girder
3 整体式连续斜板桥的实用计算方法
对于大多数设计人员来说,平面杆系有限元程序的计算理论和计算方法是较为熟悉的,对于计算结果的判断和处理也比较容易.因此本文希望可以建立基于平面杆系有限元程序的实用计算方法,使整体式连续斜板桥的计算更为方便和快捷.
本文建立整体式连续斜板桥的实用计算方法的主要思路如下所述:
选择具有代表意义的跨径4×16 m、桥宽16 m、密排支座间距1 m的的整体式连续斜板桥,计算斜交角为0°、5°、10°、15°、20°、25°、30°、35°、40°、45°的情况下,各关键截面的恒、活载主弯矩及其方向.
根据三弯矩方法,计算采用上述钢筋配置方式的钢筋方向恒、活载主弯矩.对于同一截面的不同位置,取各点位的配筋弯矩最大值作为此截面的恒、活载配筋弯矩Mx,My和M'x,M'y.如:对于边跨跨中弯矩,计算得到边跨跨中锐角自由边、板中、钝角自由边等三个关键位置的纵、横向配筋弯矩,取此三个配筋弯矩的最大值作为边跨跨中的配筋弯矩.虽然较为保守,但使设计大大简化,还是十分可取的.
采用平面杆系有限元程序,计算跨径为4×16 m的桥梁结构,各种计算参数均等价于采用板单元的空间模型.计算与上述配筋弯矩位置对应的恒、活载最大弯矩M1和M'1.
定义恒载纵向弯矩折减系数为

定义活载纵向弯矩折减系数为

定义恒载横向弯矩换算系数为

定义活载横向弯矩换算系数为

从而得到4个参数对应于不同斜交角的图表.根据平面杆系程序计算得到的弯矩,利用图表查找相应的参数,即可以得到相应的配筋弯矩,达到简化计算的目的.
各计算图表如图3~图6所示.
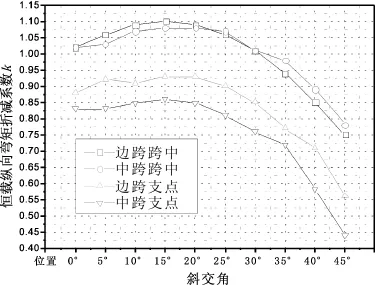
图3 恒载纵向弯矩折减系数kFig.3 Longitudinal moment reduction factor k of dead load
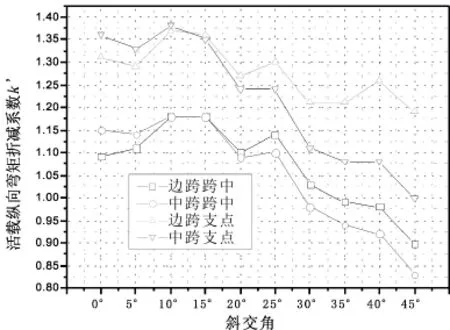
图4 活载纵向弯矩折减系数k'Fig.4 Longitudinal moment reduction factor k'of live load
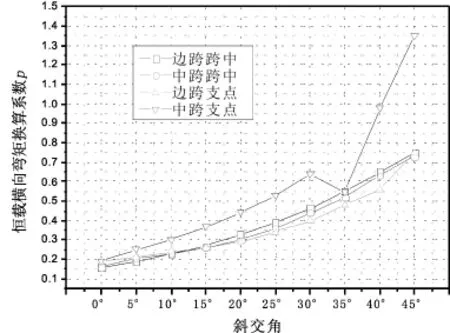
图5 恒载横向弯矩换算系数pFig.5 Transverse moment reduction factor p of dead load

图6 活载横向弯矩换算系数p'Fig.6 Transverse moment reduction factor p'of live load
由图3~图6可知,恒载作用下纵、横向弯矩随斜交角的变化规律性比较好,曲线比较圆顺;而活载作用下纵、横向弯矩随斜交角的变化离散性较大,这显然与恒、活载影响面加载方式的不同有关.
4 小结
本文根据三弯矩方法,通过大量的计算分析,给出了整体式连续斜板桥的计算图表.提出了斜板桥恒、活载最大弯矩纵横向折减系数的概念,即通过平面杆系的计算结果,查找相关系数即可以得到结构相应的配筋弯矩,大大简化了计算工作,为结构设计提供了很大便利.
[1]张士铎,袁万诚.斜交板桥的分析[J].东北林业大学学报,1986(3):126-136.
[2]郭院成.公路斜板桥结构受力特性分析[J].华北水利水电学院学报,1995(2):93-96.
[3]魏炜.钢筋混凝土斜板桥极限承载力试验[J].西安公路交通大学学报.2001(4):46-49.
[4]范立础.桥梁工程[M].北京:人民交通出版社,1996.
[5]杨炳成.整体式斜交板桥的内力计算[J].西安公路学院学报,1988(3):102-109.
(责任编辑:卢奇)
Practical calculation method of integral continuous skew girder bridges
Yang Lipo
(Tianjin Municipal Engineering Design and Research Institute,Tianjin 300051,China)
Reasonable reinforcement method was proposed for integral continuous skew girder bridges with different skew angles.Based on the three-moment method,practical calculation method was summarized and solution charts were presented through the method of theoretical calculation and finite element analysis.The result indicated that based on the calculation results of plane rod system,the reinforcement moment of bridge structure could be gotten by looking up correlation coefficients and the calculation work was greatly simplified.
integral continuous skew girder bridge;practical calculation method;finite element
R441.2
A
1008-7516(2016)01-0074-05
10.3969/j.issn.1008-7516.2016.01.016
2015-11-05
杨立坡(1979―),男,河北乐亭人,硕士,高级工程师.主要从事桥梁设计工作.
