空气弹簧频变特性研究

池茂儒, 高红星, 张卫华, 曾 京, 邬平波

(西南交通大学牵引动力国家重点实验室, 四川 成都 610031)

空气弹簧频变特性研究

池茂儒, 高红星, 张卫华, 曾 京, 邬平波

(西南交通大学牵引动力国家重点实验室, 四川 成都 610031)

为了研究空气弹簧不同物理参数对空气弹簧动态特性的影响,基于TPL-ASN空气弹簧模型的仿真软件ASDS建立了与试验工况一致的1/4车模型.利用该模型仿真分析节流孔直径、连接管路直径和长度、附加空气室体积、本体体积对空气弹簧频变特性的影响规律,并与试验结果进行对比分析.研究结果表明: TPL-ASN模型较准确地模拟不同物理参数的空气弹簧在不同激振频率下的动态特性;节流孔和连接管路对空气弹簧动态特性的影响主要体现在中频段,在低频段和高频段对空气弹簧动态特性影响较小;附加空气室对空气弹簧动态特性的影响主要体现在中低频段,在高频段对空气弹簧动态特性影响较小;空气弹簧本体对空气弹簧动态特性的影响主要体现在中高频段,在低频段对空气弹簧动态特性影响较小.

空气弹簧;频变特性;节流孔;连接管路;附加空气室;空气弹簧本体

为了减振降噪改善车辆动力学性能,空气弹簧被广泛应用于铁道车辆上[1-2],但不同物理参数的空气弹簧在不同激振频率下的动态特性差异很大,因此,空气弹簧模型的准确性直接影响车辆动力学性能的计算结果[3-4].国内外学者针对空气弹簧模型开展了大量的研究工作[5-11].这些研究工作取得了一些进展,也得到了一些应用,比较著名的有Krettek空气弹簧非线性模型和Docquier空气弹簧非线性模型[12-14].在Krettek模型中,空气弹簧本体通过节流孔与附加空气室连接,没有对连接管路进行详细建模,仅将连接管路的阻尼特性等效施加到节流孔的缩流系数中;在Docquier模型中,空气弹簧本体通过管路与附加空气室连接,没有对节流孔进行详细建模,仅将节流孔的阻尼特性等效施加到管路的阻力系数中.因此,这些上述空簧弹簧模型还不能完全准确地反映空气弹簧的非线性频变特性.

本文研究采用的空气弹簧非线性模型(TPL-ASN)[15-16]将连接管路和节流孔同时进行了考虑,模型更加完整,利用仿真与试验相结合的方法研究不同激振频率下空气弹簧物理参数对其动态特性的影响趋势.一方面验证TPL-ASN空气弹簧非线性模型的准确性,另一方面深入分析空气弹簧物理参数对其频变特性的影响规律,为空气弹簧的选型设计提供理论依据.

1 TPL-ASN空气弹簧非线性模型与试验工况介绍

空气弹簧由本体、附加空气室、节流孔、连接管路、差压阀和高度控制阀等组成,其模型示意图如图1所示.

在空气弹簧建模过程中,首先建立空气弹簧本体、附加空气室、节流孔、连接管路、差压阀和高度控制阀等多物理参数的子模型,然后利用进出气体质量流量相等的原则,将各个子模型衔接,组成一个完整的空气弹簧系统计算模型.

图1 空气弹簧模型示意Fig.1 Schematic diagram of air spring model

但在各子模型的衔接过程中,节流孔与连接管路不能直接相连,要求节流孔与连接管路的两端必须都是气室空间,否则无法衔接两个子模型,这正是空气弹簧建模的一大难点.文献[15-16]采用辅助空间法解决了节流孔和连接管路之间的衔接难题:在连接管路中截取一段作为辅助空间(如图1所示),这样节流孔一端连接本体,另一端连接辅助空间;连接管路一端连接辅助空间,另一端连接附加空气室.该空气弹簧模型称之为“辅助空间非线性模型”,简称为TPL-ASN空气弹簧模型,具体建模过程参见文献[16].

为了验证TPL-ASN模型的准确性,作者进行了大量的试验,试验台及空气弹簧的安装方式如图2所示.空气弹簧上端的质量块可以垂向自由移动,模拟车体的质量;空气弹簧下端的作动器可以施加正弦激励,模拟线路激扰.本次试验以某高速动车组空气弹簧作为试验对象,其物理参数如表1所示.

图2 空气弹簧振动试验台Fig.2 Air spring vibration test bench

名称数值 标准高度/mm200 有效面积/m20.21083 有效面积变化率/(m2·m-1)0.12512 空气弹簧本体体积/L25 附加空气室体积/L70 节流孔直径/mm14 连接管路长度/m2 连接管路直径/mm38.1

为了研究空气弹簧的频变特性,试验采用不同的激励频率(0.1～15.0 Hz)进行激振,分析空气弹簧关键物理参数(节流孔直径、连接管路直径和长度、附加空气室体积和空气弹簧本体体积)对空气弹簧频变特性的影响规律.采用自编的空气弹簧动态特性仿真软件(简称ASDS软件) 仿真分析TPL-ASN模型.

2 空气弹簧频变特性分析

为了与空气弹簧试验结果对比,仿真输入参数与试验条件完全相同:空气弹簧上端移动质量块的质量为8.65 t(1/4车体质量),试验时的环境温度始终保持12 ℃.研究在不同激振频率下空气弹簧关键物理参数(节流孔直径、连接管路直径和长度、附加空气室体积、空气弹簧本体体积)对空气弹簧动态特性(动刚度和阻尼比)的影响趋势,进而总结出空气弹簧物理参数对空气弹簧频变特性的影响规律.

2.1 节流孔直径对空气弹簧频变特性的影响

在研究节流孔直径对空气弹簧频变特性的影响规律时,节流孔直径分别选取为12.4、14.0、16.3、18.2、20.1 mm(其他物理参数见表1所示).不同节流孔直径对空气弹簧的动刚度和阻尼比影响结果分别见图3和图4所示.

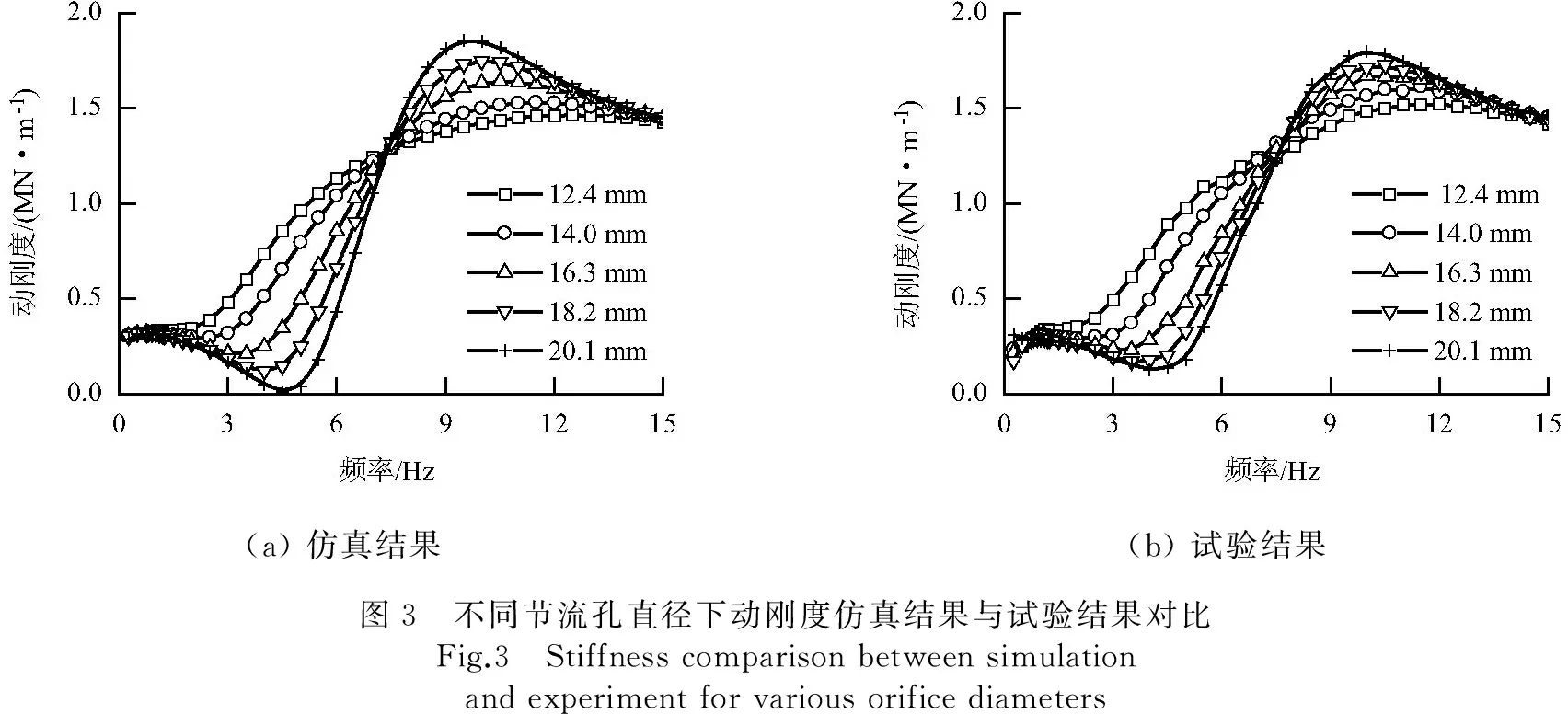
(a)仿真结果(b)试验结果图3 不同节流孔直径下动刚度仿真结果与试验结果对比Fig.3 Stiffnesscomparisonbetweensimulationandexperimentforvariousorificediameters

(a)仿真结果(b)试验结果图4 不同节流孔直径下阻尼比仿真结果与试验结果对比Fig.4 Dampingratiocomparisonbetweensimulationandexperimentforvariousorificediameters

从图3和图4可以发现如下规律:

(1) 在不同节流孔直径工况下, TPL-ASN模型仿真计算的空气弹簧动刚度和阻尼比随激振频率的变化规律与试验结果能够较好地吻合,说明TPL-ASN模型能够比较准确地模拟空气弹簧在不同节流孔直径下的频变特性.

(2) 空气弹簧的动刚度在低频段(小于2 Hz)和高频段(大于12 Hz)受节流孔直径的影响较小.在中频段(2～12 Hz),节流孔直径对空气弹簧的动刚度影响较大,而且不同节流孔直径的动刚度曲线有一个共同的交会频率(本文工况下约为8 Hz),当激励频率低于交会频率时,空气弹簧的动刚度随节流孔直径的增大而减小;当激励频率高于交会频率时,空气弹簧的动刚度随节流孔直径的增大而增大.

(3) 空气弹簧的阻尼比在低频段(小于1 Hz)和高频段(大于10 Hz)受节流孔直径的影响较小,且阻尼比在这两个频段都趋于0.在中频段(1～10 Hz),节流孔直径对空气弹簧的阻尼比影响较大,而且阻尼比在中频段存在极大值点,随着节流孔直径的增大,阻尼比极值也增大,且极值点对应的频率也增大.当激振频率较低(本文为1～4 Hz)时,空气弹簧的阻尼比随节流孔直径的增大而减小;当激振频率较高(本文为4～10 Hz)时,空气弹簧的阻尼比随节流孔直径的增大而增大.

总括起来,节流孔直径在低频段和高频段对空气弹簧动态特性影响小,而在中频段对空气弹簧动态特性影响较大.究其原因,在低频激励时,节流孔对气流的阻碍作用小;在高频激励时,节流孔对气流的阻碍作用大,本体和附加空气室之间的气体来不及通过节流孔进行交换,因此,在低频和高频区域,节流孔的作用没有发挥出来,所以空气弹簧的动态特性(动刚度和阻尼比)随节流孔直径的变化不明显.而在中频激励区,节流孔的作用被充分发挥出来,所以空气弹簧的动态特性受节流孔直径的影响很大,表现出强烈的非线性特性.

2.2 连接管路直径对空气弹簧频变特性的影响

在研究连接管路直径对空气弹簧频变特性的影响规律时,连接管路直径分别选取为12.7、25.4、38.1 mm(其他物理参数见表1所示).不同连接管路直径对空气弹簧的动刚度和阻尼比影响结果分别见图5和图6所示.

(a)仿真结果(b)试验结果图5 不同连接管路直径下动刚度仿真结果与试验结果对比Fig.5 Stiffnesscomparisonbetweensimulationandexperimentforvariouspipediameters

(a)仿真结果(b)试验结果图6 不同连接管路直径下阻尼比仿真结果与试验结果对比Fig.6 Dampingratiocomparisonbetweensimulationandexperimentforvariouspipediameters

从图5和图6可以发现如下规律:

(1) 在不同连接管路直径工况下, TPL-ASN模型仿真计算的空气弹簧动刚度和阻尼比随激振频率的变化规律与试验结果都能够较好地吻合,说明TPL-ASN模型能够比较准确地模拟空气弹簧在不同连接管路直径下的频变特性.

(2) 空气弹簧的动刚度在低频段(小于1 Hz)和高频段(大于15 Hz)受连接管路直径的影响相对较小.在中频段(1～15 Hz),连接管路直径对空气弹簧的动刚度影响较大,而且动刚度在激振频率范围内存在极大值点,随着连接管路直径的增大,动刚度极值也增大,且极值点对应的频率也增大.

(3) 空气弹簧的阻尼比在低频段(小于1 Hz)和高频段(大于13 Hz)受连接管路直径的影响较小.在中频段(1～13 Hz),连接管路直径对空气弹簧阻尼比影响较大,而且阻尼比在激振频率范围内存在极大值点,随着连接管路直径的增大,极值点对应的频率也增大.

总括起来,连接管路直径在低频段和高频段对空气弹簧动态特性影响小,而在中频段对空气弹簧动态特性影响较大.

2.3 连接管路长度对空气弹簧频变特性的影响

在研究连接管路长度对空气弹簧频变特性的影响规律时,连接管路长度分别选取为1.25、1.50、2.00 m(其他物理参数见表1所示).不同连接管路长度对空气弹簧的动刚度和阻尼比影响结果分别见图7和图8所示.

(a)仿真结果(b)试验结果图7 不同连接管路长度下动刚度仿真结果与试验结果对比Fig.7 Stiffnesscomparisonbetweensimulationandexperimentforvariouspipelengths

(a)仿真结果(b)试验结果图8 不同连接管路长度下阻尼比仿真结果与试验结果对比Fig.8 Dampingratiocomparisonbetweensimulationandexperimentforvariouspipelengths

从图7和图8可以发现如下规律:

(1) 在不同连接管路长度工况下, TPL-ASN模型仿真计算的空气弹簧动刚度和阻尼比随激振频率的变化规律与试验结果都能够较好地吻合,说明TPL-ASN模型能够比较准确地模拟空气弹簧在不同连接管路长度下的频变特性.

(2) 空气弹簧的动刚度在低频段(小于3 Hz)和高频段(大于13 Hz)受连接管路长度的影响较小.在中频段(3～13 Hz),连接管路长度对空气弹簧的动刚度有影响:空气弹簧的动刚度随连接管路长度的增大而增大.

(3) 空气弹簧的阻尼比在低频段(小于3 Hz)和高频段(大于13 Hz)受连接管路长度的影响相对较小.在中频段(3～13 Hz),连接管路长度对空气弹簧的阻尼比有影响:阻尼比在中频范围内存在极大值点(本文实验条件下约为4 Hz),随着连接管路长度的增大,阻尼比极值也增大,且极值点对应的频率略有减小.当激振频率较低时(3～5 Hz),空气弹簧的阻尼比随连接管路长度的增大而增大,当激振频率较高时(5～13 Hz),空气弹簧的阻尼比随连接管路长度的增大而减小.

总括起来,连接管路长度在低频段和高频段对空气弹簧动态特性影响小,而在中频段对空气弹簧动态特性影响相对较大.

2.4 附加空气室体积对空气弹簧频变特性的影响

在研究附加空气室体积对空气弹簧频变特性的影响规律时,附加空气室体积分别选取为30、50、70、90、110 L(其他物理参数见表1所示).不同附加空气室体积对空气弹簧的动刚度和阻尼比影响结果分别见图9和图10所示.

从图9和图10可以发现如下规律:

(1) 在不同附加空气室体积工况下, TPL-ASN模型仿真计算的空气弹簧动刚度和阻尼比随激振频率的变化规律与试验结果都能够较好地吻合,说明TPL-ASN模型能够比较准确地模拟空气弹簧在不同附加空气室体积下的频变特性.

(2) 空气弹簧的动刚度在高频段(大于13 Hz)受附加空气室体积的影响很小.在低频段(本文工况为小于4 Hz),空气弹簧的动刚度随附加空气室体积的增大而减小.在中频段(本文为4～13 Hz),空气弹簧的动刚度随附加空气室体积的增大而增大.

(3) 空气弹簧的阻尼比在高频段(大于13 Hz)受附加空气室体积的影响很小.在低频段(本文工况为小于6 Hz),空气弹簧的阻尼比随附加空气室体积的增大而增大.在中频段(本文为6～13 Hz),空气弹簧的阻尼比随附加空气室体积的增大而减小.空气弹簧的阻尼比在中低频范围内存在极大值点,随着附加空气室体积的增大,阻尼比极值也增大,但极值点对应的频率会减小.

(a)仿真结果(b)试验结果图9 不同附加空气室体积下动刚度仿真结果与试验结果对比Fig.9 Stiffnesscomparisonbetweensimulationandexperimentforvariousauxiliaryreservoirvolumes

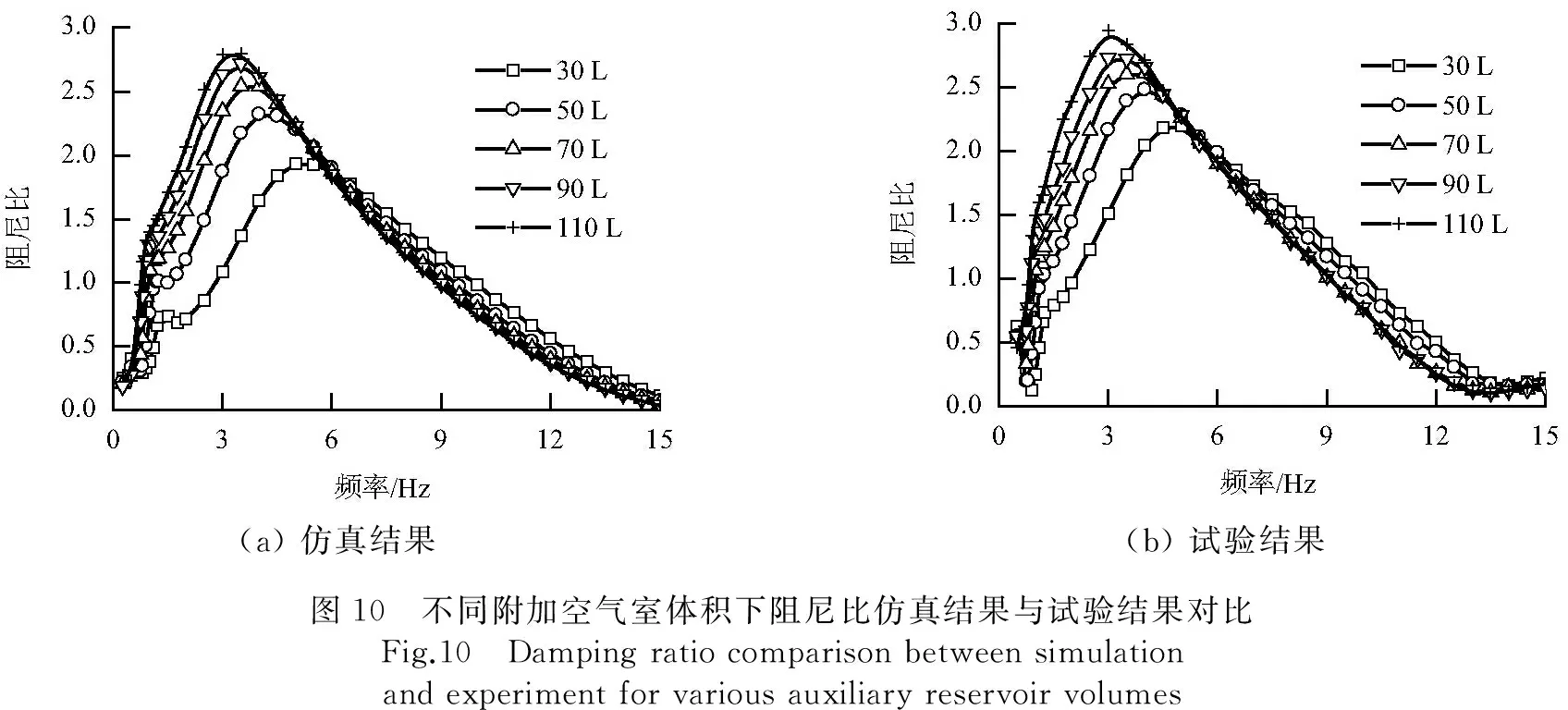
(a)仿真结果(b)试验结果图10 不同附加空气室体积下阻尼比仿真结果与试验结果对比Fig.10 Dampingratiocomparisonbetweensimulationandexperimentforvariousauxiliaryreservoirvolumes

总括起来,附加空气室体积在高频段对空气弹簧动态特性影响小,而在中低频段对空气弹簧动态特性影响较大.究其原因,主要是因为在高频激励下,由于节流孔和连接管路的阻碍作用较强,本体和附加空气室之间的气体来不及交换,相当于附加空气室在整个空气弹簧系统中基本不起作用;而在中低频激励下,节流孔和连接管路的阻碍作用较小,附加空气室的作用逐渐显著.

2.5 空气弹簧本体体积对空气弹簧频变特性的影响

在研究空气弹簧本体体积对空气弹簧频变特性的影响规律时,空气弹簧本体体积分别选取为15、25、35、45、55 L(其他物理参数见表1所示).由于改变空气弹簧本体体积在试验中难以实现,所以本文只有仿真分析,不同空气弹簧本体体积对空气弹簧的动刚度和阻尼比影响结果分别见图11和图12所示.

图11 不同本体体积下动刚度仿真结果Fig.11 Simulated stiffness for various bellow volumes

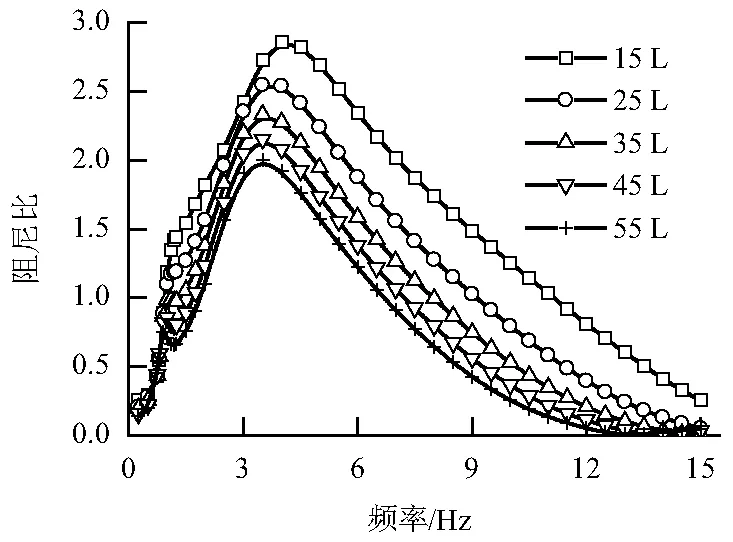
图12 不同本体体积下阻尼比仿真结果Fig.12 Simulated damping ratio for various bellow volumes

从图11和图12可以发现如下规律:

(1) 空气弹簧的动刚度在低频段(本文工况为小于3 Hz)受空气弹簧本体体积的影响很小.在中高频段(本文工况为大于3 Hz),空气弹簧动刚度随空气弹簧本体体积的增大而减小.

(2) 气弹簧的阻尼比在低频段(本文工况为小于1 Hz)受空气弹簧本体体积的影响很小.在中高频段(本文工况为大于1 Hz),空气弹簧阻尼比随空气弹簧本体体积的增大而减小.空气弹簧的阻尼比在中高频范围内存在极大值点,随着空气弹簧本体体积的增大,阻尼比极值减小,极值点对应的频率减小.

总括起来,空气弹簧本体体积在低频段对空气弹簧动态特性影响小,而在中高频段对空气弹簧动态特性影响较大.究其原因,主要是因为在低频激励下,节流孔和连接管路的阻碍作用小,本体和附加空气室相当于连通起来共同发挥作用,而本体体积相对于附加空气室体积较小,所以作用不显著;而在中高频激励下,节流孔和连接管路的阻碍作用加大,相当于切断了空气弹簧本体与附加空气室的联系,所以空气弹簧本体的作用逐渐显著.

3 结 论

通过空气弹簧物理参数对空气弹簧频变特性影响的理论与试验研究,可以得出如下结论:

(1) 在不同空气弹簧物理参数(节流孔直径、连接管路直径和长度、附加空气室体积)工况下,TPL-ASN模型仿真计算的空气弹簧动刚度和阻尼比随激振频率的变化规律与试验结果能够较好地吻合,说明TPL-ASN模型能够较准确地模拟空气弹簧的频变特性;

(2) 节流孔和连接管路对空气弹簧动态特性的影响主要体现在中频段,而在低频段和高频段对空气弹簧动态特性影响较小;

(3) 附加空气室对空气弹簧动态特性的影响主要体现在中低频段,而在高频段对空气弹簧动态特性影响较小;

(4) 空气弹簧本体对空气弹簧动态特性的影响主要体现在中高频段,而在低频段对空气弹簧动态特性影响较小.

需要指出,本文主要是针对某动车组特定空气弹簧展开的单一物理参数影响研究(在分析某一物理参数的影响时假定其他物理参数不变),如果有多个物理参数同时变化,空气弹簧的非线性频变特性将变得十分复杂,有待进一步深入研究.

[1] 张利国,张嘉钟,贾力萍,等. 空气弹簧的现状及其发展[J]. 振动与冲击,2007,26(2): 146-151.

ZHANG Liguo, ZHANG Jiazhong, JIA Liping, et al. Future and development of air springs[J]. Journal of Vibration and Shock, 2007, 26(2): 146-151.

[2] 严隽耄,傅茂海. 车辆工程[M]. 3版.北京:中国铁道出版社,2009: 79-88.

[3] 任晋峰. 高铁车辆车体振动基础性研究[D]. 大连:大连交通大学,2012.

[4] 张广世. 铁道车辆空气弹簧动力学模型的研究[D]. 上海:同济大学汽车学院,2006.

[5] 金炜东,吕乾勇,孙永奎. 基于Copula函数的高速列车转向架故障特征提取[J]. 西南交通大学学报,2015,50(4): 676-682.

JIN Weidong, LV Qianyong, SUN Yongkui. Extracting fault features of high-speed train bogies using copula function[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 676-682.

[6] EVANS J, BERG M. Challenges in simulation of rail vehicle dynamics[J]. Vehicle System Dynamics, 2009, 47(8): 1023-1048.

[7] KUNIEDA M. Theory and experiment on vertical vibration of rolling stock equipped with air springs[J]. Railway Technical Research Report, 1958, 3(6): 17-27.

[8] ODA N, NISHIMURA S. Vibration of air suspension bogies and their design[J]. Bulletion of the JSME, 1970, 13(55): 43-50.

[9] SHIMOZAWA K, TOHTAKE T. An air spring model with non-linear damping for vertical motion[J]. Quarterly Report of RTRI, 2008, 49(4): 209-214.

[10] QUAGLIA G, SORLI M. Air suspension dimensionless analysis and design procedure[J]. Vehicle System Dynamics, 2001, 35(6): 443-475.

[11] NIETO A J, MORALES A L, GONZALEZ A, et al. An analytical model of pneumatic suspensions based on an experimental characterization[J]. Journal of Sound and Vibration, 2008, 313: 290-307.

[12] DOCQUIER N, FISETTE P, JEANMART H. Model-Based evaluation of railway pneumatic suspensions[J]. Vehicle System Dynamics, 2008, 46(Sup. 1): 481-493.

[13] DOCQUIER N, FISETTE P, JEANMART H. Multiphysic modelling of railway vehicles equipped with pneumatic suspensions[J]. Vehicle System Dynamics, 2007, 45(6): 505-524.

[14] FACCHINETTI A, MAZZOLA L, ALFI S, et al. Mathematical modelling of the secondary airspring suspension in railway vehicles and its effect on safety and ride comfort[J]. Vehicle System Dynamics, 2010, 48(Sup.): 429-449.

[15] 高红星,池茂儒,朱旻昊,等. 空气弹簧模型研究[J]. 机械工程学报,2015,51(4): 108-115.

GAO Hongxing, CHI Maoru, ZHU Minhao, et al. Study on air spring model[J]. Journal of Mechanical Engineering, 2015, 51(4): 108-115.

[16] 池茂儒,高红星,张卫华,等. 基于辅助空间的空气弹簧非线性模型[J]. 中国铁道科学,2014,35(3): 83-89.

CHI Maoru, GAO Hongxing, ZHANG Weihua, et al. Nonlinear model of airspring based on auxiliary space[J]. China Railway Science, 2014, 35(3): 83-89.

池茂儒(1973—),博士,2005年起至今任职于西南交通大学,现为牵引动力国家重点实验室研究员,博士生导师,教育部新世纪优秀人才.主要研究方向为高速动车组系统动力学、重载货运长大列车运行安全性、城市轻轨车辆设计理论及控制.先后主持国家自然基金项目1项、国家科技支撑计划课题3项、省部级项目2项,参与国家重大项目50余项,主研校企合作项目200多项,获得国家专利10余项,发表论文60余篇，获国家科技进步二等奖1项、铁道部科学技术一等奖3项、企业科技创新奖2项.国家自然科学基金项目评审专家，《交通技术》杂志编委.

E-mail: cmr2000@163.com

高红星(1989—),博士研究生,研究方向为铁道车辆系统动力学.参与国家重大项目5项,发表论文6篇,获得国家专利5项,硕士毕业论文《铁道车辆空气弹簧动态特性研究》获西南交通大学优秀硕士论文.

E-mail: gaohongxingvip@163.com

(中文编辑:秦 瑜 英文编辑:兰俊思)

Frequency-Dependent Characteristics of Air Spring

CHIMaoru,GAOHongxing,ZHANGWeihua,ZENGJing,WUPingbo

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

In order to study the influence of different physical parameters of an air spring on its dynamic characteristics, a quarter-car model consistent with experimental conditions was set up using the simulation software ASDS that is based on the TPL-ASN air spring model. With the model, influence laws of orifice diameter, connecting pipe diameter and length, auxiliary reservoir volume, and air spring bellow volume on frequency-dependent characteristics was simulated and analyzed. The simulation results were compared with the experimental results. The results show that the TPL-ASN model can accurately simulate the nonlinear characteristics of an air spring with different physical parameters at different excitation frequencies. The influence of the orifice and connecting pipe on dynamic characteristics of air spring is mainly reflected in the middle frequency range, and is less affected in low and high frequency ranges. The influence of the auxiliary reservoir volume on dynamic characteristics of air spring is mainly reflected in low and middle frequency ranges, and is less affected in the high frequency range. The influence of the air spring bellow volume on dynamic characteristics is mainly reflected in middle and high frequency ranges, and is less affected in the low frequency range.

air spring; frequency-dependent characteristics; orifice; connecting pipe; auxiliary reservoir; air spring bellow

2015-10-16

国家自然科学基金重点资助项目(61134002); 国家自然科学基金高铁联合基金资助项目(UI334206)

池茂儒,高红星,张卫华,等. 空气弹簧频变特性研究[J]. 西南交通大学学报,2016,51(2): 236-243.

0258-2724(2016)02-0236-08

10.3969/j.issn.0258-2724.2016.02.003

U271.91

A