轮轨高速滚动接触及钢轨疲劳裂纹扩展研究
2016-04-06江晓禹李孝滔曹世豪
江晓禹, 李孝滔, 李 煦, 曹世豪
(1. 西南交通大学力学与工程学院, 四川 成都 610031; 2. 西南交通大学土木工程学院, 四川 成都 610031)
轮轨高速滚动接触及钢轨疲劳裂纹扩展研究
江晓禹1, 李孝滔1, 李 煦1, 曹世豪2
(1. 西南交通大学力学与工程学院, 四川 成都 610031; 2. 西南交通大学土木工程学院, 四川 成都 610031)
为研究高速列车轮轨滚动接触疲劳损伤,通过引入应变率效应,获得了轮轨接触作用力的分布,并基于最大周向应力判据,对车轮滚过裂纹过程中裂纹可能的扩展角度进行了统计分析,确定了钢轨表面疲劳裂纹的扩展方向.根据威布尔分布,用可能扩展角度均值作为裂纹扩展方向,获得了裂纹扩展路径.研究结果表明,低速列车钢轨的裂纹扩展为张开型裂纹逐渐变为滑开型裂纹,高速列车的钢轨裂纹扩展基本都是张开型裂纹;高速列车钢轨的裂纹扩展速率快于低速列车钢轨;模拟的裂纹路径与实验测得的裂纹路径吻合,验证了用可能扩展角度的均值作为裂纹扩展方向的合理性.
滚动接触疲劳;有限元;裂纹扩展;威布尔分布
轮轨接触疲劳一直是铁路工业中难以解决的问题,对于高速线路尤其严重[1].这增加了运营成本,直接危害了列车安全.轮轨接触疲劳破坏机制比较复杂,到目前为止还有很多不清楚的地方,吸引了大量学者研究.高速铁路钢轨的主要损伤形式是疲劳裂纹扩展[2].钢轨经过多次碾压后,产生塑性变形层[3].裂纹扩展到一定程度后,其扩展速率将变小[4].
钢轨裂纹的扩展行为是轮轨接触疲劳分析的重要内容.关于裂纹扩展方向的判断,产生了很多理论,最常用的有最大周向应力理论[5]、最小应变能密度因子理论[6]、最大能量释放率理论[7]以及Richard的一个经验判据[8].这些理论基本解决了比例单调加载的情况,而对于随机载荷谱作用下的裂纹扩展方向问题,需要在裂纹尖端建立一段相对于主裂纹无穷小的支裂纹,认为裂纹的扩展方向为支裂纹KⅠ最大的方向、ΔKⅠ最大的方向或者ΔKeff最大的方向等.很多研究者用这种方法来判断裂纹的扩展方向[9-14],但这种方法尚未成熟,这类判据的应用条件存在争议,现在只是用已知的实验结果来推断用哪一个判据更接近实验结果,还不能用这类判据来确定裂纹方向.
车轮的滚动造成裂纹扩展的加载路径与常规疲劳实验不同,其扩展角度存在不确定性,因此,本文采用概率统计的方法来分析裂纹扩展角度,并初步论证了用可能扩展角度的均值作为裂纹扩展角度的合理性.
1 理论介绍
1.1 研究模型
轮轨接触的研究模型如图1所示,车轮以水平速度v在钢轨上向前滚动,车轮在钢轨上作稳态滚动(此时刻列车的加速度为0,车轮与钢轨之间无整体滑动,但在接触区存在局部滑动和粘着),轮重为G,驱动力偶矩为Me,风阻力为Fw,在车轮滚动前方的钢轨表面存在微裂纹.轮轨间的接触作用力分布为接触压力p和摩擦力f.

图1 轮轨滚动接触研究模型Fig.1 The rolling contact model of wheel/rail
1.2 轮轨接触的应变率效应
由于车轮在钢轨上作高速滚动,轮轨接触区的变形速率较快,会出现较大的应变率.而钢轨材料U71Mn钢在较大的应变率下,会表现出明显的应变率效应.在国产热轧U71Mn钢轨上取样,制取顺纤维方向的试件,可得U71Mn钢的应变率特征[15]:
(1)

σs0=550 MPa为材料在准静态时的屈服极限(一般在不考虑速度或较低速度时可采用其作为钢轨材料的屈服极限);
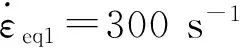



(2)
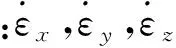

ν为材料的泊松比.
1.3 裂纹尖端的最大周向应力理论
1963年Erdogan和Sih提出了最大周向应力准则[5],他们认为裂纹将向周向拉应力最大的方向扩展.利用这个假设可以得出裂纹的扩展角度:
(3)
式中:θ为裂纹扩展角度,规定θ逆时针为正,顺时针为负.在裂纹尖端建立1/4节点的奇异性单元和一个x轴与裂纹共线、y轴与裂纹面垂直的局部坐标,如图2,根据位移外推法可计算出裂纹尖端的应力强度因子,如下式[17]:
(4)
(5)
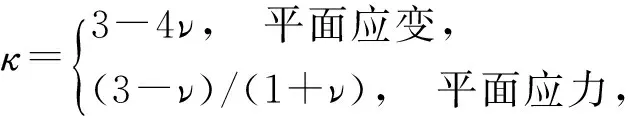
(6)
式中:E为弹性模量;ν为泊松比;L为单元长度;ui和vi为各节点在局部坐标下x方向和y方向的位移,如图2所示.
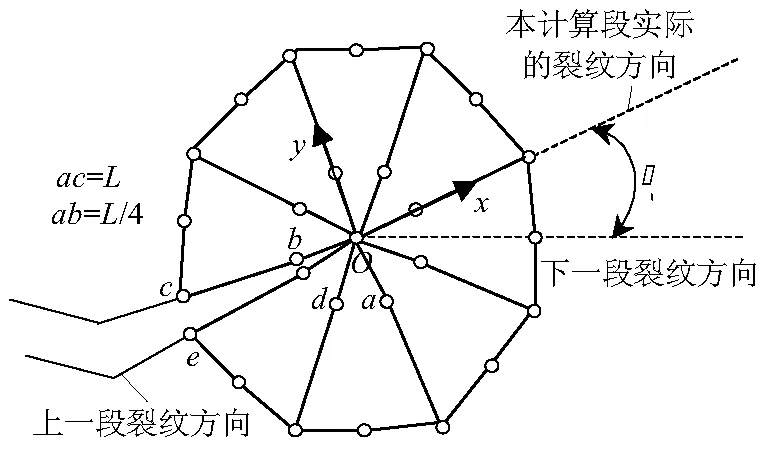
图2 裂纹尖端1/4节点单元Fig.2 Quarter-points elements at the crack tip
1.4 裂纹扩展的威布尔分布
式(7)为威布尔分布的密度概率函数,式(8)为累加概率函数.
(7)
(8)
式中:γ为位置参数;β为形状参数,β取不同的值,可得到正偏、负偏和对称的概率密度函数;α为尺度参数,反映分布的分散情况.
数据是否服从威布尔分布,可以用概率坐标纸法进行判断[18].对式(8)作变换可得:
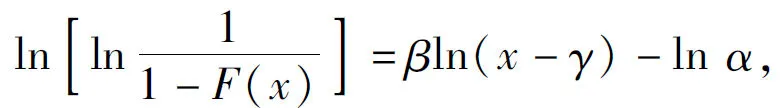
(9)
令

(10)
式中:xi为随机变量,如果(Xi,Yi)呈直线分布,则数据服从威布尔分布.
1.5 裂纹扩展的非参数bootstrap方法
对于已知一个容量为n的来自某一分布的数据样本,而总体分布情况未知的问题,可以用bootstrap方法来对总体分布进行统计推断[19].设:
x=(x1,x2,…,xn)
(11)
是来自总体为F的一个已知样本,相继、独立地用放回抽样的方法从此样本中得到B个相同样本容量的bootstrap样本,求出每一个样本的均值,自小到大排序:
ω(1)≤ω(2)≤…≤ω(B),
(12)
记:
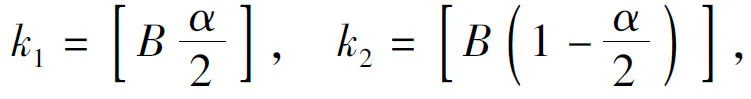
(13)
那么就可以得到均值的置信度为1-α的bootstrap置信区间:
(14)

2 有限元模拟
本研究采用的材料为U71Mn钢,其力学性能[16,20]如表1.

表1 U71Mn钢的力学性能Tab.1 Material parameters of U71Mn steel
建立2D的有限元模型,钢轨高为176 mm,长为1 000 mm;车轮直径为900 mm,边界条件为钢轨底部全约束.
本研究主要对比不同的列车运行速度情况下,轮轨的接触作用力分布变化,及钢轨表面微裂纹扩展速率等的不同.取列车运行速度350 km/h(高速)和50 km/h(低速)进行研究,轮重为5 t,车轮在钢轨上作稳态滚动(即为无整体滑动的情况),列车运行速度为50 km/h时作用在单个车轮上的等效风阻力为38N,350 km/h时为1 018N(按8节车厢的CRH3型高速列车获得[21-22]).
而研究钢轨表面微裂纹的扩展时,需考虑到裂纹尖端的应力奇异性,钢轨有限元整体模型和裂纹尖端局部模型如图3所示.
从图3(b)可以看到初始裂纹.规定裂纹角度为裂纹的长度方向与行车方向的夹角,初始裂纹长度为100 μm,初始角度为30°.
轮轨滚动接触疲劳过程中,裂纹尖端受随机载荷谱的作用(即使在车轮滚过裂纹的一个周期内,裂纹的受载也无法用常规的正弦波或锯齿波等表示),车轮滚过裂纹过程中裂纹尖端的载荷谱会出现多个峰值,即相当于出现多个循环.一方面由于低应力幅值对裂纹扩展影响很小,另一方面由于超载迟滞效应,出现波峰后的裂纹扩展速率将变得很低,对于此类情况的疲劳分析,一般截除低应力幅值的载荷段[23].

(a) 整体模型

(b) 裂纹尖端局部模型图3 含微裂纹钢轨裂纹有限元模型Fig.3 Finite element modal of rail crack
同时,车轮滚过裂纹过程,裂纹尖端周向最大拉应力方向一直处于变化之中,裂纹扩展角度具有不确定性,因此用概率统计的方法来对裂纹扩展角度进行分析.样本的总体为截除后的载荷段.抽样的原则为:每个循环内抽取同样多的样本;单个循环内加载和卸载过程等距抽取相同数量的样本.
具体的裂纹扩展路径分析过程为:初始钢轨表面裂纹100 μm,角度30°,根据车轮滚过该裂纹过程,获得裂尖应力强度因子的分布,然后通过概率统计方法,确定下一段(100 μm长)裂纹的扩展角度;重复计算,再获得下一段裂纹的扩展角度,以此类推,直到获得整个裂纹的扩展路径.
3 结果与讨论
3.1 轮轨接触作用力分布
在考虑轮轨高速滚动时材料快速变形所引起的应变率效应和高速列车很大风阻力情况下,可获得轮轨接触作用力如图4.图4中横坐标表示轮轨接触区尺寸,纵坐标分别为分布接触压力p和分布摩擦力f,50 km/h和 350 km/h表示车速.从图4中可见,高速滚动时的法向接触压力p与低速情况表现出较大的不同,低速滚动时接触压力分布与Hertz接触应力分布相近,而高速滚动情况出现两个峰值,因此,高速列车的轮轨接触压力不能简单的用Hertz接触压力代替.摩擦力f分布不同主要由很大的风阻力引起.而这种接触作用力分布的不同将进一步影响到钢轨表面微裂纹扩展速率和破坏模式.

图4 轮轨滚动接触作用力的分布Fig.4 Distribution of contact forces between wheel and rail
3.2 微裂纹扩展
车轮滚过裂纹时,随着车轮位置的变化,裂纹尖端周向拉应力最大的方向也在不断地变化,因此裂纹扩展方向具有不确定性.计算出车轮处于不同位置处裂纹尖端周向拉应力最大的方向,用概率统计的方法对其分析.
列车速度分别为50 km/h和350 km/h的条件下,计算裂纹尖端等效应力强度因子Keff,用其来表示KⅠ和KⅡ的共同作用[8],其表达式为
(15)
裂纹扩展路径上Keff的变化情况如图5.

图5 裂纹尖端Keff随裂纹长度的变化Fig.5 Keff at crack tip varies with the length of crack
从裂纹扩展速率的影响因素来看(根据Paris公式,ΔKeff越大,裂纹扩展越快;而车轮滚过裂纹后,裂尖的应力强度因子为零,因此Keff最大值就等于ΔKeff的最大值),350 km/h时的等效应力强度因子Keff最大值的保持时间要大于50 km/h的情况,因此350 km/h时的裂纹扩展速率要大于50 km/h.
裂纹尖端应力强度因子KⅠ和KⅡ随裂纹长度变化的情况,图6为不同车速下钢轨表面裂纹尖端应力强度因子随裂纹长度的变化.从图6(a)可见,车速为50 km/h时,钢轨裂纹在扩展过程中开始是KⅠ占主导,逐渐变成KⅡ占主导.从图6(b)可以看出350 km/h列车钢轨裂纹在扩展过程中基本都是是KⅠ占主导.

(a)车速50km/h(b)车速350km/h图6 不同车速下钢轨表面裂纹尖端应力强度因子随裂纹长度的变化Fig.6 Stressintensityfactoratcracktipvarieswiththelengthofthecrackfordifferenttrainspeed
图5和图6(a)中的曲线在裂纹长度为1.3 mm时出现了明显的拐点,这是由于裂纹急剧的偏转引起的.裂纹在向下扩展阶段,KⅡ不断地增大,裂纹上下错动剧烈.当裂纹急剧偏转后,裂纹向行车相反的方向扩展,裂纹的上下剧烈错动得到很大的缓解,裂纹尖端应力得到放松,因此KⅡ和Keff急剧地减小.
速度为50 km/h和350 km/h的列车车轮滚过钢轨裂纹的整个过程中,分别对每一段裂纹可能的扩展角度进行统计分析,结果如表2和表3.

表2 车速为50 km/h列车钢轨裂纹扩展角度的统计结果Tab.2 Statistical results of rail crack propagation angle for 50 km/h train
表中,相关系数是用概率坐标纸法对数据进行拟合得到的,它表示的是数据服从威布尔分布的可能性,l=0.955意味着数据有95.5%的可能性服从威布尔分布.
从表2可以看出,列车速度为50 km/h,钢轨裂纹长度不大于1 mm时(每段裂纹长度为100 μm,即10段裂纹的总长),相关系数均大于95%,在此阶段裂纹可能的扩展角度服从威布尔分布的可能性较大;裂纹长度大于1 mm而小于1.4 mm的阶段,相关系数均小于86%,扩展角度服从威布尔分布的可能性相对较小;当裂纹长度大于1.4 mm后,即裂纹急剧向行车反方向扩展后,相关系数均大于97.5%,在此阶段裂纹可能的扩展角度服从威布尔分布的可能性很大.
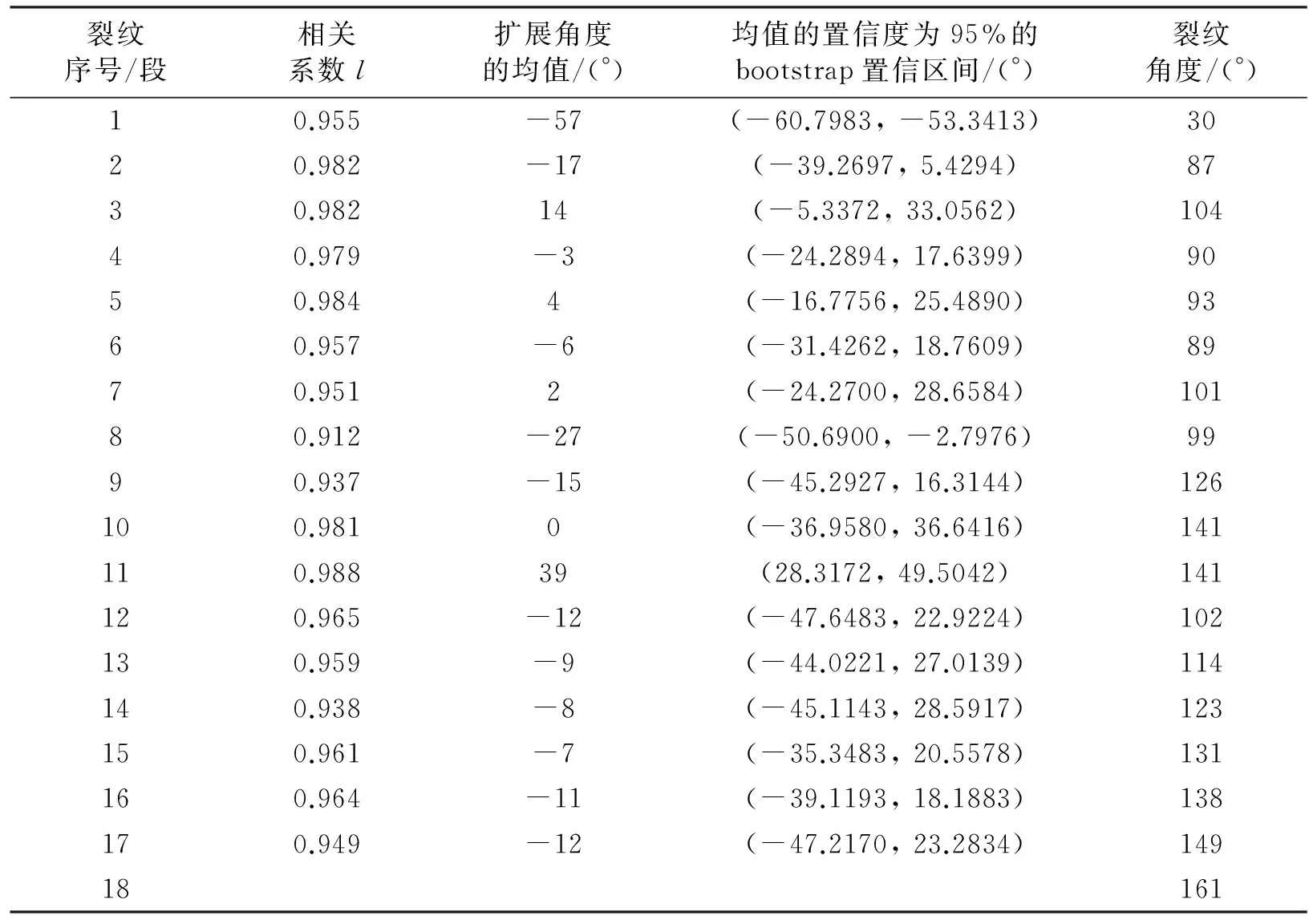
表3 车速为350 km/h列车钢轨裂纹扩展角度的统计结果Tab.3 Statistical results of rail crack propagation angle for 350 km/h train
从表3可以看出,列车速度为350 km/h时,其钢轨裂纹扩展路径上的相关系数均大于90%,而且只有4段裂纹相关系数小于95%.因此,列车速度为350 km/h时钢轨裂纹扩展过程中的绝大部分阶段,裂纹可能的扩展角度服从威布尔分布的概率较大.
将列车速度为50 km/h和350 km/h条件下有限元模拟的裂纹扩展路径和实验测得的大秦线服役钢轨裂纹路径[24]对比,如图7.
从图7(a)和(b)可以看到,速度为50 km/h的列车和350 km/h的列车钢轨裂纹扩展路径的大致趋势都是初始阶段与列车运行方向成锐角扩展,第二阶段与列车运行方向基本成90°向钢轨内部扩展,最后阶段沿与列车运行方向相反的方向扩展,这与大秦线服役钢轨测得的裂纹路径吻合.因此,用裂纹可能扩展角度的均值作为裂纹的扩展方向是可行的.同时,从图7(a)和(b)对比可见,高速时,裂纹扩展在向深度前进过程中,更早的出现了偏转,这可能会导致更早的出现剥离破坏.

(a)模拟的时速50km/h列车(b)模拟的时速350km/h列车(c)大秦线服役钢轨裂纹路径图7 模拟的裂纹扩展路径与实验测得的裂纹扩展路径对比Fig.7 Comparisonofcrackpathbetweensimulationandexperiment
4 结 论
(1) 速度为50 km/h和350 km/h列车的轮轨接触作用力具有明显不同的分布形式.高速列车轮轨接触压力不能简单的用Hertz接触压力代替.
(2) 速度为50 km/h和350 km/h列车钢轨裂纹扩展模式不同.50 km/h时钢轨裂纹由张开型为主逐渐变为滑开型;而350 km/h钢轨裂纹基本上都是以张开型为主.且高速列车钢轨的裂纹扩展速率快于低速列车钢轨.
(3) 对于速度为50 km/h的列车,其钢轨裂纹长度不大于1 mm以及大于1.4 mm的阶段,裂纹可能的扩展角度服从威布尔分布的可能性较大.对于 350 km/h列车钢轨裂纹扩展过程中的绝大部分阶段,裂纹可能的扩展角度服从威布尔分布的概率都较大.
(4) 模拟的裂纹扩展路径与服役钢轨测得裂纹路径的扩展趋势基本一致,因此,用裂纹可能扩展角度的均值作为裂纹的扩展方向是可行的.
[1] 金学松,沈志云. 轮轨滚动接触疲劳问题研究的最新进展[J]. 铁道学报,2001,2(2): 92-108.
JIN Xuesong, SHEN Zhiyun. Rolling contact fatigue of wheel /rail and its advanced research progress[J]. Journal of the China Railway Society, 2001, 2(2): 92-108.
[2] EKBERG A, KABO E, NIELSEN J C O, et al. Subsurface initiated rolling contact fatigue of railway wheels as generated by rail corrugation[J]. International Journal of Solids & Structures, 2007, 44(24): 7975-7987.
[3] GARNHAM J E, DAVIS C L. The role of deformed rail microstructure on rolling contact fatigue initiation[J]. Wear, 2008, 265(9): 1363-1372.
[4] CANADINC D, SEHITOGLU H, VERZAL K. Analysis of surface crack growth under rolling contact fatigue[J]. International Journal of Fatigue, 2008, 30(9): 1678-1689.
[5] ERDOGAN F, SIH G C. On the crack extension in plates under plane loading with transverse shear[J]. Journal of Basic Eng Asme, 1963, 85: 519-527.
[6] SIH G C. Mechanics of fracture method of analysis and solution of crack problems[J]. NoordHoff Int. Publishers, 1973, 5: 10-16.
[7] PALANISWAMY K, KNAUSS W G. Propagation of crack under general in-plane tension[J].International Journal of Fracture, 1972, 8: 114.
[8] RICHARD H A, FULLAND M, SANDER M. Theoretical crack path prediction[J]. Fatigue Fract Engng Mater Struct, 2005, 28: 3-12.
[9] DUBOURG M C, LAMACQ V. A predictive rolling contact fatigue crack growth model: onset of branching, direction, and growth-role of dry and lubricated conditions on crack patterns[J]. J Tribol Transact ASME, 2002, 124(4): 680-688.
[10] HOURLIER F, PINEAu A. Propagation of fatigue cracks under polymodal loading[J]. Fatigue & Fracture of Engineering Materials & Structures, 1982, 5(4): 287-302.
[11] BAIETTO M C, PIERRES E, GRAVOUIL A, et al. Fretting fatigue crack growth simulation based on a combined experimental and XFEM strategy[J]. International Journal of Fatigue, 2013, 47(1): 31-43.
[12] TROLL B, BAIETTO M C, GRAVOUIL A, et al. 2D fatigue crack propagation in rails taking into account actual plastic stresses[J]. Engineering Fracture Mechanics, 2014, 123(1): 163-181.
[13] BROUZOULIS J, EKH M. Crack propagation in rails under rolling contact fatigue loading conditions based on material forces[J]. International Journal of Fatigue, 2012, 45(3): 98-105.
[14] BAIETTO M C, PIERRES E, GRAVOUIL A. A multi-model X-FEM strategy dedicated to frictional crack growth under cyclic fretting fatigue loadings[J]. International Journal of Solids & Structures, 2010, 47(10): 1405-1423.
[15] BOYCE B L, DILMORB M F. The dynamic tensile behavior of tough ultrahigh-strength steels at strain-rates from 0.000 2 s-1to 200 s-1[J]. International Journal of Impact Engineering, 2009, 36: 263-271.
[16] 田越,程育仁,刘学文. 高应变率下U71Mn轨钢动态力学性能研究[J]. 中国铁道科学,1992,13: 34-42.
TIAN Yue, CHENG Yuren, LIU Xuewen. Studies on the dynamic behaviors of U71Mn rail steel under high strain rates[J]. China Railway Science, 1992, 13: 34-42
[17] ALEGRE J M, CUESTA I I. Some aspects about the crack growth FEM simulations under mixed-mode loading[J]. International Journal of Fatigue, 2010, 32(7): 1090-1095.
[18] 高镇同,熊峻江. 疲劳可靠性分析[M]. 北京:北京航空航天大学出版社,2000: 79-84
[19] 盛骤,谢式千,潘承毅. 概率论与数理统计[M]. 北京:高等教育出版社,2008: 276-282.
[20] 周小林,向延念,陈秀方. U71Mn50 kg·m-1普通碳素钢钢轨疲劳裂纹扩展速率试验研究[J]. 中国铁道科学,2004,25(3): 86-90.
ZHOU Xiaolin, XIANG Yannian, CHEN Xiufang. Test and study of fatigue fracture propagation of U71Mn50 kg·m-1ordinary carbon steel rail[J]. China Railway Science, 2004, 25(3): 86-90.
[21] 姚拴宝,郭迪龙,杨国伟,等. 高速列车气动阻力分布特性研究[J]. 铁道学报,2012,34(7): 18-23.
YAO Shuanbao, GUO Dilong, YANG Guowei, et al. Distribution of high-speed train aerodynamic drag[J]. Journal of the China Railway Society, 2012, 34(7): 18-23.
[22] 毛军,郗艳红,杨国伟. 列车编成辆数对高速列车横风气动特性影响的数值分析[J]. 中国铁道科学,2012,33(1): 78-85.
MAO Jun, XI Yanhong, YANG Guowei. Numerical analysis on the influence of train formation on the aerodynamic characteristics of high speed trains under crosswind[J]. China Railway Science, 2012, 33(1): 78-85.
[23] 郦正能,张纪奎. 工程断裂力学[M]. 北京:北京航空航天大学出版社,2012: 191-195.
[24] 郭火明,王文健,刘腾飞,等. 重载铁路钢轨损伤行为分析[J]. 中国机械工程,2014,25(2): 269-270.
GUO Huoming, WANG Wenjian, LIU Tengfei, et al. Analysis of damage behavior of heavy-haul railway rails[J]. China Mechanical Engineering, 2014, 25(2): 269-270.

江晓禹(1965—),博士,1998年起至今任职于西南交通大学,现为力学与工程学院教授,博士生导师.研究方向为轮轨接触疲劳、复合材料力学.承担国家自然科学基金、863科技攻关计划、中国科学院创新工程等重要研究项目多项,发表研究论文60余篇,编著高校教材3部.中国力学学会教育工作委员会委员、四川省力学学会理事.
E-mail:xiaoyujiang8@sohu.com.

李孝滔(1991—),博士研究生.研究方向为疲劳与断裂.
E-mail:1293657604@qq.com.
(中、英文编辑:徐 萍)
Research on Wheel/Rail Rolling Contact at High Speed and Fatigue Crack Propagation in Rail
JIANGXiaoyu1,LIXiaotao1,LIXu1,CAOShihao2
(1. School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
To analyze the rolling contact fatigue damage of wheel/rail for high-speed trains, the distribution of contact forces between wheel and rail was obtained by introducing the strain-rate effect. Based on the maximum circumferential stress, the possible propagation angle of the crack was counted when a wheel roll over a crack and the crack propagation directions were determined. According to the Weibull distribution, crack path was obtained by using the average crack propagation angle as the crack propagation direction. The results show that the crack mode becomes to sliding crack from opening crack for low-speed trains. The crack mode is always opening crack for high-speed trains. The crack propagation velocity for high-speed trains is faster than that of low-speed trains. The simulation crack path is in agreement with the experimental crack path, which proves that it is reasonable to use the average crack propagation as crack propagation direction.
rolling contact fatigue; finite element; crack propagation; Weibull distribution
2015-10-23
国家自然科学基金资助项目(11472230); 国家自然科学基金重点资助项目(U1134202,E050303); 四川省青年科技创新团队资助项目(2013TD0004)
江晓禹,李孝滔,李煦,等. 轮轨高速滚动接触及钢轨疲劳裂纹扩展研究[J]. 西南交通大学学报,2016,51(2): 274-281.
0258-2724(2016)02-0274-08
10.3969/j.issn.0258-2724.2016.02.007
U211.5
A
