空间向量在求线面角中的应用

周明星

（甘肃省陇南市武都区两水中学）

探索篇·方法展示

空间向量在求线面角中的应用

周明星

（甘肃省陇南市武都区两水中学）

以空间几何体为载体考查空间角与空间距离是历年高考命题的重点与热点，而考查的重心又以线面角和二面角为主，常以解答题的形式进行考查，空间向量在处理立体几何问题时具有很大的优越性，能把推理性问题具体化、运算化，即通过点的坐标和平面的法向量，把立体几何中的平行、垂直、线面角、二面角、距离等关系用向量的方式表达出来，使立体几何问题简单化。

立体几何；空间向量；法向量；线面角

以空间几何体为载体考查空间角与空间距离是历年高考命题的重点与热点，而考查的重心又以线面角和二面角为主，常以解答题的形式进行考查，空间向量在处理立体几何问题时具有很大的优越性，能把推理性问题具体化、运算化，即通过点的坐标和平面的法向量，把立体几何中的平行、垂直、线面角、二面角、距离等关系用向量的方式表达出来，使立体几何问题简单化。

空间向量的应用难度主要体现在如何巧妙建立空间直角坐标系和坐标的准确运算上，空间向量解决立体几何问题绕开了复杂的作图、论证、推理，只需通过坐标运算进行求解。

空间向量应用的核心思想是转化，利用空间直角坐标系，通过向量的运算解答问题，达到几何问题代数化的目的，同时还要注意，坐标运算的准确性，一丝一毫的马虎将全盘皆输。

空间向量解决线面角时，关键在于“四破”：（1）破“建系关”，即构建恰当的空间直角坐标系；（2）破“坐标关”，即准确求出相应各点的坐标；（3）破“法向量关”，即准确求解平面的法向量；（4）“公式关”，即准确应用公式求解。

下面，我就利用法向量求解线面角大小的基本方法与具体思路作简单的说明。

一、空间向量解线面角的原理及解法

已知：平面α与直线l交于A点，求直线l与平面α所成的角。

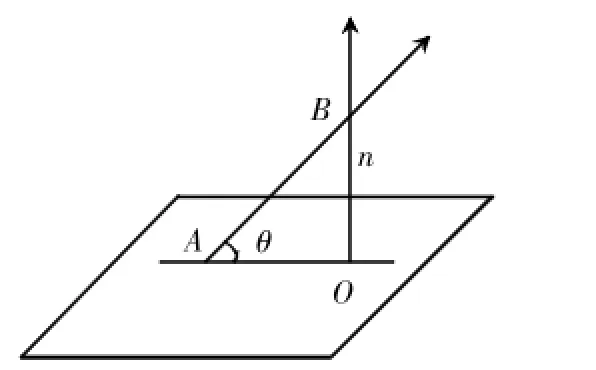
图1

取直线上的任意向量AB，如图1所示：

二、应用举例

例1.如图2所示，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=2，AF=1，求直线DF与平面ACEF所成角的正弦值；

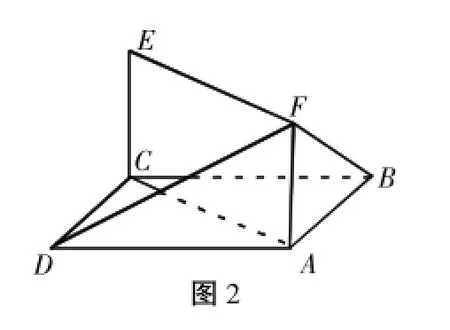
图2

解：如图3，以C为坐标原点，CD为x轴正向，CB为y轴正向，CE为z轴正向，建立直角坐标系O-xyz，A（2，2，0），B（0，2，0），C（0，0，0），D（2，0，0），F（2，2，1），E（0，0，1），连接BD，则AC⊥BD.

图3

因为平面ABCD⊥平面ACEF，且平面ABCD∩平面ACEF= AC，所以是平面ACEF的一个法向量。

例2.在正方体ABCD—A1B1C1D1中，点E为BB1的中点，求BD与平面A1ED所成角的正弦值。

图4

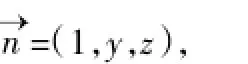
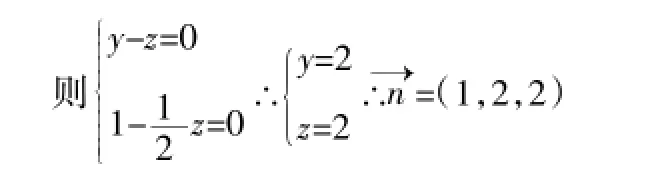
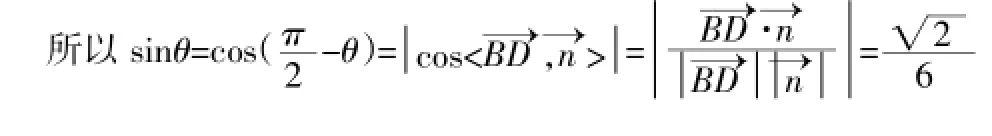
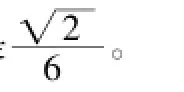
三、几点说明

立体几何，是高考6道解答题中的必考题，向量法是解决立体几何问题的一种常用方法。与传统方法（即：几何法）相比，向量法对思维能力要求比较低，并且解题思路简洁、清晰，可操作性强。

然而，在用向量法解决问题中，学生经常会遇到一些困惑：

1.不会恰当建系。

2.不能熟练求解个别关键点的坐标。而这两个问题中恰当建系是基础，也是关键。因为恰当建立空间直角坐标系，往往可以简化运算，使问题变得简洁、明了。

3.可以直接建系的几何体都有一个共同的特点：在几何体中,都存在或隐含有三条两两垂直的线（三条线不一定共点）；建系时，坐标原点往往设在交叉位置或几何体的对称位置。

通过以上例题，我们发现立体几何的点面、线面、面面之间的关系都可以统一为空间向量的计算，而要研究线面角则可以从它们的方向向量和法向量入手，通过空间向量的夹角公式来解决。

立体几何让三维空间变得更充实，向量法又给此类问题的解决插上了腾飞的翅膀。要用向量法解题，就得先建系！而恰当建系是向量法解题的前提和关键。希望我今天的发言能给大家有所帮助，如有不足，请多多指教！

［1］乔全福.空间向量在立体几何中的应用［J］.青海教育，2014.

［2］郭明甫.向量法解立体几何探索性命题“三部曲”［J］.高中数学教与学，2011.

·编辑鲁翠红